Книга: Экономическая теория. Полный курс МВА
Назад: 6. Функции двух переменных. Частные производные
Дальше: Статистическое приложение
7. Две основные проблемы микроэкономики. Метод Лагранжа
Проблема 1. Достижение максимальной полезности при заданных затратах.
Пусть полезность набора (х, у) моделируется функцией U = xy. Предположим, что цены товаров равны 3 и 2, а имеющийся в наличии капитал равен Q = 24. Требуется израсходовать этот капитал так, чтобы получить максимальную полезность.
Математически это означает, что нужно найти максимум функции U – xy c учетом того, что количества товаров х и у удовлетворяют условию Зх + 2у = 24.
Проблема 2. Достижение минимальных затрат при заданной полезности.
Предположим, что требуется купить набор (х, у) с заданной полезностью U= 6, но требуется сделать это так, чтобы затрата Q = Зх + 2у была минимальной.
Математически это означает, что нужно найти минимум функции Q = Зх + 2у с учетом того, что количества товаров x и у удовлетворяют условию ху = 6.
Обе эти проблемы являются задачами на условный экстремум. Задача на условный экстремум формулируется в общем случае так: найти экстремум (максимум или минимум) функции z = (x, y), если х и у удовлетворяют условию g(x, у) = 0.
Задача эта решается по методу Лагранжа следующим образом.
1. Составляем функцию Лагранжа L(x, у, λ). Для этого к оптимизируемой функции прибавляем условие, умноженное на параметр λ: L(x, у, λ) = f(x, у) + λg{x, у).
2. Функция Лагранжа зависит от трех переменных. Берем от нее частные производные по каждой из переменных и приравниваем их к нулю. Получаем систему трех уравнений с тремя неизвестными:
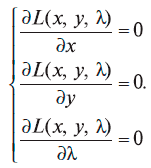
3. Решаем эту систему и получаем оптимальные значения х и у (значение вспомогательного параметра λ нас не интересует, его можно отбросить).


Решите самостоятельно следующие задачи.
1. Цены товаров X и Y равны соответственно 7 и 5 за единицу товара. Сколько единиц товаров X и Y следует купить на сумму Q = 105, чтобы функция полезности U=х²у была максимальной?
2. Цены товаров X и Y равны соответственно 18 и 12 за единицу товара. Какую минимальную сумму следует затратить на приобретение этих товаров для того, чтобы функции полезности U = х³у³ приняла значение U = 32?
3. Цены товаров Х и Y равны соответственно 5 и 4 за единицу товара. Сколько единиц товаров X и Y следует купить на сумму Q = 60, чтобы функция полезности U = xy² была максимальной?
4. Цены товаров Х и Y равны соответственно 4 и 1 за единицу товара. Какую минимальную сумму следует затратить на приобретение этих товаров для того, чтобы функции полезности U = х²у приняла значение U = 21
Замечание для сторонников неоправданного ригоризма.
Автор прекрасно отдает себе отчет в том, что 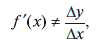 даже если приращения Δх и Δу малы. Однако определение производной через отношение малых приращений вместо общепринятого
даже если приращения Δх и Δу малы. Однако определение производной через отношение малых приращений вместо общепринятого 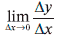 – обладает несомненной наглядностью и большей доступносгью для начинающих экономистов, математическая подготовка которых часто далека от высоких стандартов университетского курса математического анализа.
– обладает несомненной наглядностью и большей доступносгью для начинающих экономистов, математическая подготовка которых часто далека от высоких стандартов университетского курса математического анализа.
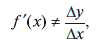 даже если приращения Δх и Δу малы. Однако определение производной через отношение малых приращений вместо общепринятого
даже если приращения Δх и Δу малы. Однако определение производной через отношение малых приращений вместо общепринятого 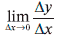 – обладает несомненной наглядностью и большей доступносгью для начинающих экономистов, математическая подготовка которых часто далека от высоких стандартов университетского курса математического анализа.
– обладает несомненной наглядностью и большей доступносгью для начинающих экономистов, математическая подготовка которых часто далека от высоких стандартов университетского курса математического анализа.

