Пусть фирма А и фирма В выпускают одну и ту же продукцию и пусть прибыль у зависит от объема х выпускаемой продукции. Предположим, что для фирмы А зависимость прибыли от объема продукции моделируется функцией у = 10х – х₂. Это означает, что при объеме продукции х = 4 прибыль фирмы А будет равна у = 24. Пусть для фирмы В та же зависимость моделируется функцией у = 14х – х2. Тогда при объеме продукции х = 2 прибыль фирмы В будет равна у = 24.

Итак, прибыли обеих фирм одинаковы. Однако прибыль, приходящаяся на единицу продукции у фирмы А, равна у/х = 6, в то время как у фирмы В она равна у/х = 12. Фирма В, таким образом, более рентабельна. Из этого следует, что наряду с величиной у полезно рассматривать также величину у/х.

Обобщим эти рассуждения на случай произвольной функции. Пусть дана зависимость у = f(x). Значения функции у при данном значении л: будем называть суммарной величиной. Значение суммарной величины, поделенное на х, будем называть средней величиной. Итак,

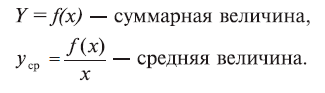
Средняя величина суммарной величины f(x) обозначается в экономике через Af(x) (обозначение не очень удачное, так как можно принять его за умножение функции на число А).

Выясним геометрический смысл средней величины и характер ее поведения. Рассмотрим график некоторой функции (рис. 13).

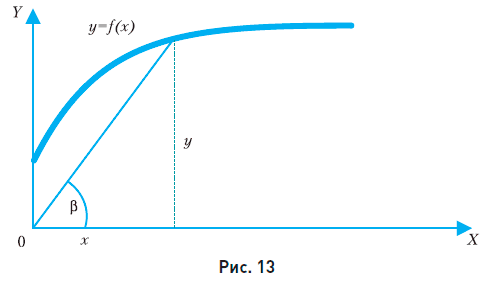
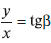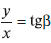Из рисунка видно, что средняя величина равна и она убывает с ростом х, так как убывает угол наклона прямой, идущей из начала координат в данную точку.

Задача 12. Нарисовать график возрастающей и выпуклой вниз функции (какой у нее будет знак второй производной?), для которой средняя величина возрастает.

Итак, для заданной суммарной величины f(x) можно по графику находить в каждой точке среднее значение Af(x), определяя координаты каждой точки и находя их отношение.

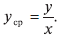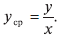Поставим обратную задачу. Пусть дан график среднего значения уср = Af(x) (рис. 14). Требуется по графику определить в данной точке значение у = f(x) суммарной величины. По определению Отсюда можно найти у = ycpx (площадь закрашенного прямоугольника). Это и есть значение суммарной функции f(x).

Наряду со средним значением Af(x) суммарной величины f(x), которое можно рассматривать как глобальную скорость изменения суммарной величины, определяют также локальную скорость изменения суммарной величины, т. е. ее производную f'(x) (см. п. 2). Эту величину называют маржинальной (или предельной) величиной суммарного значения и обозначают Mf(x). С использованием среднего и маржинального значений суммарной величины можно получить следующее выражение эластичности:

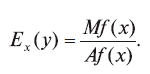
По данному суммарному значению f(x) можно найти предельное значение Mf(x) при помощи дифференцирования или геометрически через тангенс угла наклона (см. п. 2).

Поставим обратную задачу: по данному предельному значению Mf(x) найти суммарное значение f(x). Математически это сводится к задаче о нахождении функции по ее производной. Такая операция называется интегрированием и выполняется при помощи табл. 3.

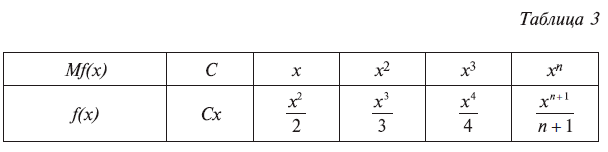
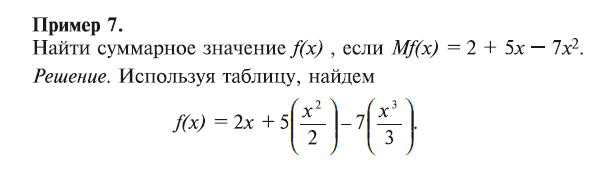
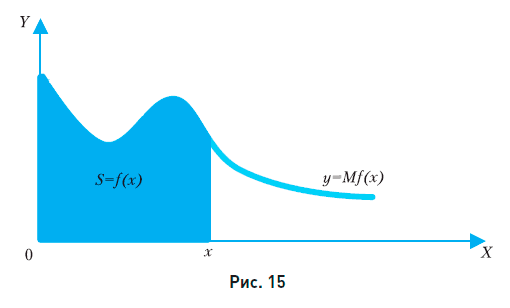
Задача 13. Найти f(x), если Mf(x) = 5х³ – х² + 1. Геометрически по данному графику у = Mf(x) суммарное значение f(x) в данной точке x определяется как площадь S под кривой на участке от 0 до x (рис. 15).