Книга: Экономическая теория. Полный курс МВА
Назад: 3. Вторая производная, ее геометрический смысл
Дальше: 5. Суммарные, средние и предельные величины в экономике
4. Эластичность
Мы уже исследовали поведение функции, применяя понятие скорости роста. Скорость роста функции в точке определялась через отношение 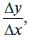 которое характеризует чувствительность изменения величины у при изменении величины х. При этом для определения чувствительности функции в данной точке мы предполагали, что приращения Δх и Δу являются малыми величинами. Однако величины этих приращений зависят от выбора единиц измерения: если Δх = 0,1 еще можно считать малой величиной, то Δх = 300 таковой уже не назовешь. А ведь это одна и та же величина, измеренная в первом случае, например, в долларах, а во втором – в копейках. Чтобы избежать такого рода противоречий, в экономике рассматривают относительные приращения (приращения величины, отнесенные к общему количеству величины), т. е. величины
которое характеризует чувствительность изменения величины у при изменении величины х. При этом для определения чувствительности функции в данной точке мы предполагали, что приращения Δх и Δу являются малыми величинами. Однако величины этих приращений зависят от выбора единиц измерения: если Δх = 0,1 еще можно считать малой величиной, то Δх = 300 таковой уже не назовешь. А ведь это одна и та же величина, измеренная в первом случае, например, в долларах, а во втором – в копейках. Чтобы избежать такого рода противоречий, в экономике рассматривают относительные приращения (приращения величины, отнесенные к общему количеству величины), т. е. величины 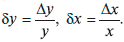 Эти относительные приращения не зависят от выбора единицы измерения. Их отношение характеризует относительную чувствительность величины у, ее реакцию на относительное изменение величины х. При малых значениях величин δх и δу это отношение называется эластичностью величины у по величине х:
Эти относительные приращения не зависят от выбора единицы измерения. Их отношение характеризует относительную чувствительность величины у, ее реакцию на относительное изменение величины х. При малых значениях величин δх и δу это отношение называется эластичностью величины у по величине х: 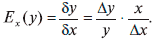
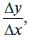 которое характеризует чувствительность изменения величины у при изменении величины х. При этом для определения чувствительности функции в данной точке мы предполагали, что приращения Δх и Δу являются малыми величинами. Однако величины этих приращений зависят от выбора единиц измерения: если Δх = 0,1 еще можно считать малой величиной, то Δх = 300 таковой уже не назовешь. А ведь это одна и та же величина, измеренная в первом случае, например, в долларах, а во втором – в копейках. Чтобы избежать такого рода противоречий, в экономике рассматривают относительные приращения (приращения величины, отнесенные к общему количеству величины), т. е. величины
которое характеризует чувствительность изменения величины у при изменении величины х. При этом для определения чувствительности функции в данной точке мы предполагали, что приращения Δх и Δу являются малыми величинами. Однако величины этих приращений зависят от выбора единиц измерения: если Δх = 0,1 еще можно считать малой величиной, то Δх = 300 таковой уже не назовешь. А ведь это одна и та же величина, измеренная в первом случае, например, в долларах, а во втором – в копейках. Чтобы избежать такого рода противоречий, в экономике рассматривают относительные приращения (приращения величины, отнесенные к общему количеству величины), т. е. величины 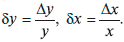 Эти относительные приращения не зависят от выбора единицы измерения. Их отношение характеризует относительную чувствительность величины у, ее реакцию на относительное изменение величины х. При малых значениях величин δх и δу это отношение называется эластичностью величины у по величине х:
Эти относительные приращения не зависят от выбора единицы измерения. Их отношение характеризует относительную чувствительность величины у, ее реакцию на относительное изменение величины х. При малых значениях величин δх и δу это отношение называется эластичностью величины у по величине х: 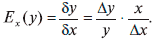
Чтобы уточнить, что эластичность вычисляется в данной точке при малых приращениях, ее называют предельной, или точечной эластичностью.
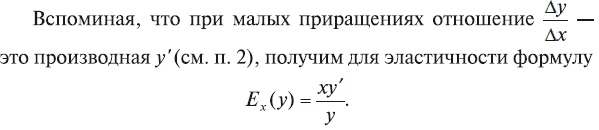
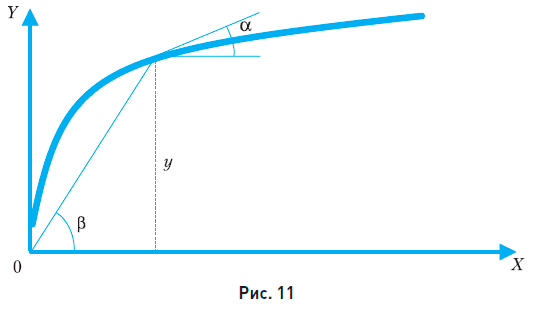
Исследуем геометрический смысл эластичности в данной точке. Для этого запишем эластичность в виде 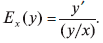 Из геометрического смысла производной известно, что у' = tgα, где α – угол наклона касательной (рис. 11), а дробь (у/х) = tgβ, где угол β – это угол, образованный с осью X отрезком, идущим из начала координат в данную точку (рис. 11).
Из геометрического смысла производной известно, что у' = tgα, где α – угол наклона касательной (рис. 11), а дробь (у/х) = tgβ, где угол β – это угол, образованный с осью X отрезком, идущим из начала координат в данную точку (рис. 11).
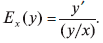 Из геометрического смысла производной известно, что у' = tgα, где α – угол наклона касательной (рис. 11), а дробь (у/х) = tgβ, где угол β – это угол, образованный с осью X отрезком, идущим из начала координат в данную точку (рис. 11).
Из геометрического смысла производной известно, что у' = tgα, где α – угол наклона касательной (рис. 11), а дробь (у/х) = tgβ, где угол β – это угол, образованный с осью X отрезком, идущим из начала координат в данную точку (рис. 11).
Поэтому для точечной эластичности получаем формулу
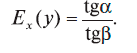
Применим эту формулу к исследованию зависимости, изображенной на рис. 12.
В точке А угол α наклона касательной меньше, чем угол β наклона отрезка ОА. Поэтому в этой точке при x = x1 эластичность меньше единицы. Зависимость в этой точке не является эластичной.
В точке В отрезок, идущий из начала координат в эту точку, совпадает с касательной, т. е. α = β. Следовательно, в этой точке при x = x2 эластичность равна единице.
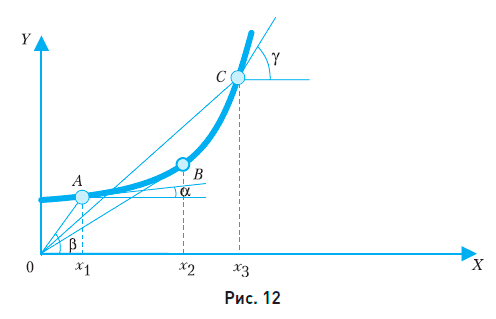
В точке С наклон касательной больше, чем наклон отрезка ОС. Следовательно, в этой точке при х = х3 эластичность больше единицы, зависимость в данной точке является эластичной.
Назад: 3. Вторая производная, ее геометрический смысл
Дальше: 5. Суммарные, средние и предельные величины в экономике

