Пусть дана функция у = х³ + х². Найдем от нее производную у' = Зх² + 2х. Эта производная также является функцией от х, и можно попытаться найти от нее производную. Эта производная от производной называется второй производной: у" = 6х + 2.

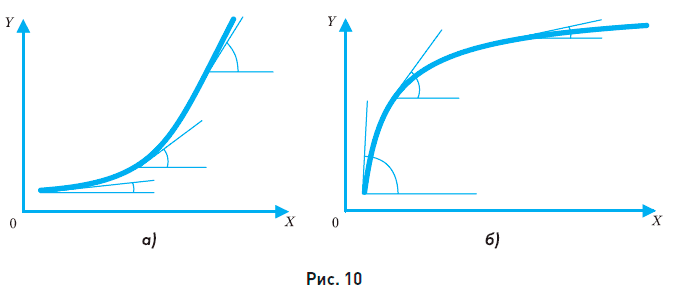
Вспомним, что знак первой производной показывает возрастание или убывание функции. Соответственно знак второй производной показывает возрастание или убывание первой производной, т. е. возрастание или убывание угла наклона кривой. Если у" > 0, то первая производная возрастает. Значит, возрастает угол наклона. А это означает, что кривая является выпуклой вниз (рис. 10, а). У функций с таким графиком скорость роста увеличивается.

Если же у"< 0, то первая производная убывает. Это означает, что убывает угол наклона и что кривая является выпуклой вверх (рис. 10, б). У функций с таким графиком скорость роста уменьшается.

Итак, знак второй производной характеризует изменение скорости роста функции: если у"> 0, то скорость роста функции увеличивается (график становится более крутым), если же у"< 0, то скорость роста функции уменьшается (график становится более пологим).

Задача 10. Рассмотреть график, изображенный на рис. 2, и выяснить, увеличивается или уменьшается скорость роста функции Торнквиста.

Пример 6. Графиком функции у = ах² + bх + с является парабола. Вторая производная у"= 2а. Если а > 0, то парабола выпукла вниз (ветви направлены вверх). А если а < 0, то парабола выпукла вверх (ветви направлены вниз).

Задача 11. Изобразить график функции, у которой первая производная отрицательная, а вторая – положительная (убывает и выпукла вниз). Разобрать другие комбинации знаков первой и второй производных.