Рассмотрим функцию у = 2х + 3. Если х = 1, то у = 5. Увеличим аргумент х на пять единиц (это увеличение называется приращением аргумента и обозначается Δх).

Новое значение аргумента будет равно х = 6, а новое значение функции будет равно у = 15. Видно, что с увеличением х на Δх = 5 функция также выросла на величину Δу = 10.

Задача 2. Найти приращение функции у = 5х + 1, если x = 3, а Δх = 2.

(Ответ: Δу = 10).

Итак, приращения Δу у двух рассмотренных функций одинаковые. Означает ли это, что обе эти функции растут одинаково быстро? Нет, так как для получения одинакового увеличения у в первом случае мы должны увеличить аргумент x на 5 единиц, а во втором – только на 2. Поэтому важен не абсолютный рост функции, а ее относительный рост. Показатель относительного роста (скорость роста) характеризуется величиной

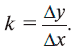
Для первой функции к = 2, для второй к = 5. Это означает, что вторая функция растет быстрее.

Две рассмотренные функции принадлежат к классу линейных функций, общий вид которых задается формулой у = кх + b. Графиком линейной функции является прямая.

Рассмотрим геометрический смысл уже введенных понятий «приращение аргумента», «приращение функции» и «показатель относительного роста».

На рис. 7 изображены график линейной функции у = kx + b и две точки на нем – Δ(х, у) и В(х + Δх, у + Δу).

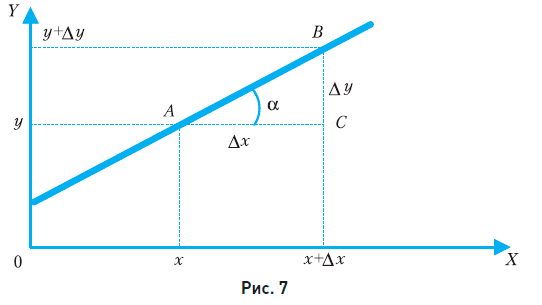
Из треугольника ABC видно, что показатель относительного роста равен

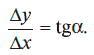
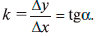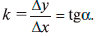Можно убедиться, что для линейной функции показатель относительного роста (скорость роста) равен коэффициенту при х в уравнении прямой у = кх + b (см. приведенные выше примеры 1 и 2), т. е. Это означает, что скорость роста связана с наклоном прямой. Чем больше угол наклона прямой, тем больше показатель относительного роста к, тем больше скорость роста. Так как для линейной функции скорость роста к связана с углом, величину к называют еще угловым коэффициентом. Знак углового коэффициента указывает на характер изменения функции (плюс – функция возрастает, минус – функция убывает).

Задача 3. Найти угловой коэффициент у рассмотренной ранее линейной функции (2).

Рассмотрим функцию, не являющуюся линейной. Графиком такой функции будет кривая линия (рис. 8).

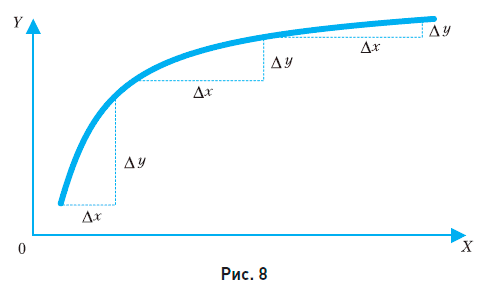
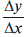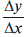Видно, что для таких функций показатель относительного роста (скорость роста) будет меняться от точки к точке. В случае, изображенном на рис. 8, видно, что угол наклона уменьшается, и поэтому уменьшается скорость роста.

С целью нахождения показателя относительного роста (скорости роста) данной функции в данной точке М проведем в этой точке касательную к графику функции (рис. 9).

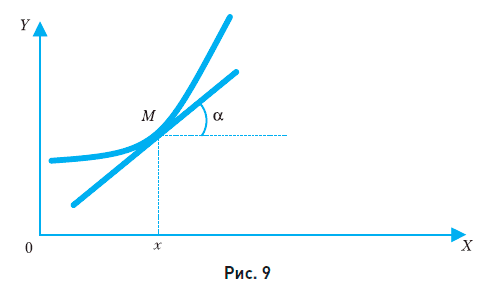
Можно считать, что вблизи точки М кривая и касательная совпадают, т. е. вблизи этой точки графиком функции является прямая линия, а сама функция вблизи данной точки является линейной.

Уже было установлено, что для линейной функции показатель относительного роста функции равен k = tgα. Это и есть скорость роста данной функции в данной точке. Но величина k меняется от точки к точке, так как меняется угол наклона. Следовательно, можно сказать, что показатель относительного роста k (скорость роста) является функцией от х. Эта функция называется производной от данной функции y = f(x) и обозначается как y = f'(х).

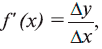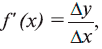Итак, производная от данной функции в данной точке – это тангенс угла наклона касательной к оси X, т. е. f'(x) = tgα. И одновременно производная – это показатель относительного роста (скорость роста) функции в данной точке, т. е. где Δx и Δу следует принимать очень малыми для того, чтобы находиться вблизи данной точки.

В экономике скорость роста в данной точке (производная) называется предельной величиной. Знак производной определяет характер изменения данной функции; если у' > 0, то функция возрастает, если у' < 0, то функция убывает.

Используя терминологию экономистов, можно сказать, что связь переменных положительная при положительной производной и отрицательная при отрицательной производной.

Задача 4. Нарисовать график какой-нибудь функции, у которой производная отрицательная; положительная.

Задача 5. Определить по графику знак производной у рассмотренной выше функции Торнквиста (см. рис. 2).

Задача 6. Пусть x – цена продукта, а у — спрос на этот продукт. Как исходя из здравого смысла ведет себя функция у с увеличением х? Какой знак имеет производная этой функции? Аналогичные вопросы для случая, когда x – это цена продукта, а у — предложение данного продукта.

Операция нахождения производной от данной функции называется дифференцированием. Продифференцировать данную функцию – значит найти производную этой функции.

Для нахождения производных конкретных функций мы будем пользоваться табл. 1.

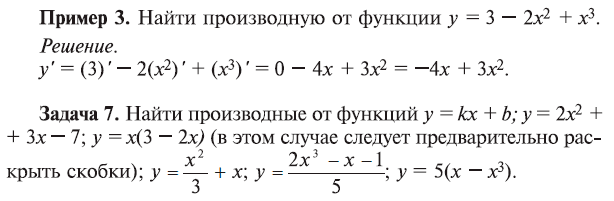
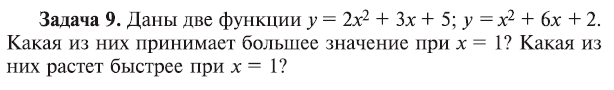
Пример 5. Определить оптимальный объем x производства, если прибыль у моделируется зависимостью у = 2х2 – 12х + 25.

Исследуем поведение функции у = 2х² — 12х + 25. Найдем ее производную у' = 4х – 12 и приравняем ее к нулю. Получим x = 3. Если объем производства хменяется от 0 до 3, то производная от прибыли отрицательная, и поэтому прибыль у убывает от 25 при x = 0 (при отсутствии производства) до 7 при x = 3. При x > 3 производная становится положительной и прибыль начинает возрастать, достигая значения 25 при x = 6, а затем при x > 6 превышает это значение.

Следовательно, в зависимости от возможностей фирмы можно:

а) ничего не делать (х = 0) и получать прибыль у = 25 в виде арендной платы;

б) поднапрячься и достичь объема производства x > 6. Тогда прибыль превысит значение 25, получаемое при отсутствии производства.

Эти выводы подтверждаются табл. 2.

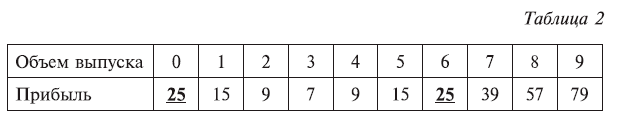
Провести аналогичное исследование для случая, когда зависимость прибыли у от объема производства х моделируется функцией у = х2 — 10х + 30.