Если две величины связаны между собой, то говорят, что между ними существует функциональная зависимость. Одну из этих величин (любую) называют аргументом, или независимой переменной, другую – зависимой переменной, или функцией.

Пусть, например, х₁ и х₂ – количества товаров, их цены – Р₁ и Р₂, а сумма, затраченная на их покупку, равна Q. Тогда между величинами х₁ и х₂ существует связь

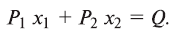
Считая х₁ функцией, а х₂ аргументом, найдем эту функцию:

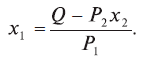
Если же функцией считать х₂, а аргументом – х₁ то функциональная зависимость будет иметь вид

Обычно в математике аргумент обозначают буквой х, а функцию – буквой y. Функциональная зависимость в этом случае будет иметь вид формулы у = f(x). Задавая произвольным образом независимую переменную х, найдем по этой формуле величину у, т. е. точку с координатами (х, у) на координатной плоскости.

Вычисляя несколько таких точек и соединяя их, получим кривую, характеризующую зависимость функции от аргумента (график данной функции).

Например, рассмотренную зависимость (1) можно записать в виде

График этой зависимости приведен на рис. 1.

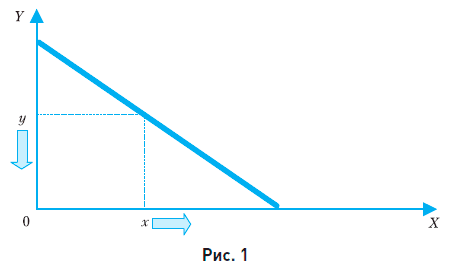
Видно, что с ростом количества товара х количество товара у уменьшается (денег на него остается меньше). Такие функции называются убывающими (в экономике такую зависимость называют отрицательной).

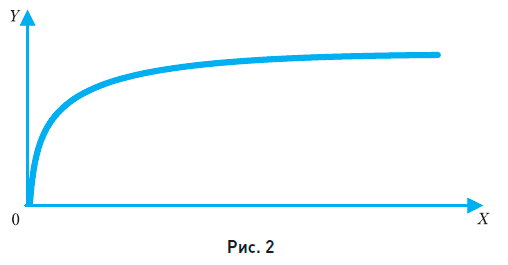
Другой пример – зависимость Торнквиста между величиной дохода х и величиной потребительского спроса у на товары первой необходимости:

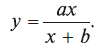
Из графика этой зависимости, изображенного на рис. 2, видно, что чем больше доход х, тем больше спрос у. Такие функции называются возрастающими (в экономике такая связь величин называется положительной).

Возрастающие и убывающие функции визуально различают очень просто: график возрастающей функции идет вверх, «в гору», график убывающей – вниз, «под гору».

Задача 1. Пусть у — численность лиц, получающих доход выше величины х. Зависимость у от x дается в этом случае формулой Парето

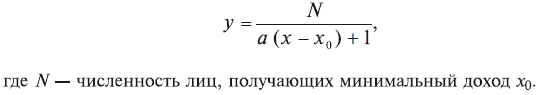
График этой зависимости показан на рис. 3.

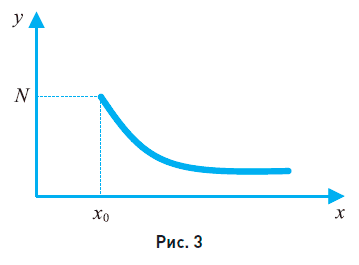
Определить, является эта функция возрастающей или убывающей. Согласуется ли поведение данной функции со здравым смыслом?

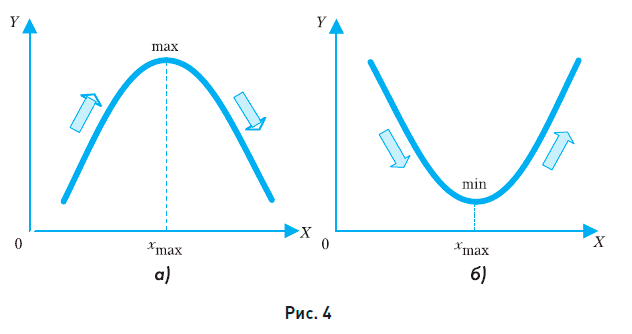
Если функция сначала возрастает, а затем, начиная с некоторого значения х, убывает, то при этом значении x она принимает максимальное значение (рис. 4, а).

Если же функция сначала убывает, а затем возрастает, то она имеет минимум (рис. 4, б).

Рассмотрим зависимость дохода фирмы у от объема производства х (рис. 5).

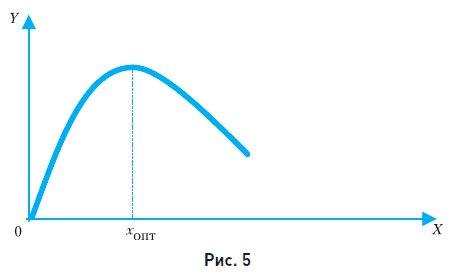
Вначале с ростом объема производства доход фирмы растет, так как увеличивается объем продаж товара. Затем, при больших объемах производства, происходит затоваривание, снижение объема продаж и, как следствие, снижение дохода. Максимальный доход получается при оптимальном объеме производства х_опт.

Рассмотрим изменение доходов двух фирм (А и Б) во времени (рис. 6).

Фирма А имеет больший доход, но скорость роста ее дохода во времени (наклон кривой) уменьшается. Фирма Б имеет меньший доход, но у нее скорость роста дохода увеличивается во времени (растет наклон кривой). Поэтому фирма Б является более перспективной.

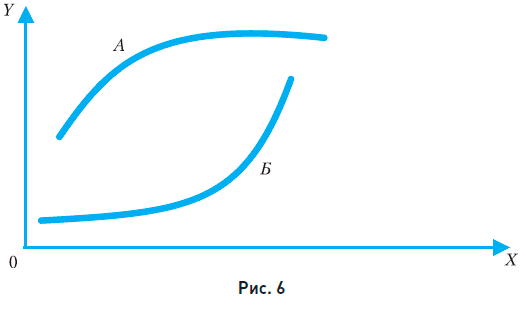
Таким образом, важным является не только характер поведения функции (возрастание или убывание; в этом примере обе функции – возрастающие), но и скорость изменения функции.

Чтобы исследовать поведение конкретной заданной функции, т. е. определить, является она возрастающей или убывающей, имеет ли она максимумы и минимумы, какова скорость изменения функции, понадобится понятие производной.