На что не способен компьютер: парадоксальное мышление
Сравнивать человеческий мозг с компьютером можно только очень условно. От «думающих» машин человека однозначно отличает способность не просто иметь дело с парадоксами, но еще и радоваться им. Компьютеры парадоксов не выносят. Столкнувшись с ними, они безнадежно зависают.
Классический парадокс возникает, когда некое утверждение вытекает из самого себя и при этом дает некие указания на степень своей истинности. Так бывает, например, когда человек утверждает, что он всегда лжет. Из этого заявления невозможно сделать вывод о том, насколько оно истинно. Проще всего, конечно, посчитать подобные формулировки философской белибердой, но из них можно извлечь какую-то информацию, а заодно и понаблюдать за тем, как работает собственный мозг, постоянно натыкаясь на какие-то ограничения.
Возьмем простую формулировку: «Это утверждение ложно». Вроде бы все понятно, но давайте задумаемся. Если исходить из того, что человек говорит правду, значит, это утверждение действительно ложно. Если же человек, произносящий эту фразу, лжет, значит, утверждение правдиво. Возникает противоречие, с которым мозг не в состоянии справиться, и нам остается только удивляться. На базе этой основополагающей структуры великие мыслители создали огромное множество поразительных и занимательных вариаций. Одна из самых известных приписывается критскому философу Эпимениду: «Все критяне – лжецы». Оставим вне рассмотрения вопрос, хорошо ли выносить сор из избы, и вместо этого задумаемся, имеем ли мы в данном случае дело с истинным парадоксом. Если принять это утверждение на веру, то ему нельзя верить, потому что Эпименид сам критянин и, следовательно, говорит неправду. Но если Эпименид лжет, то из этого необязательно следует, что все критяне говорят правду. Истинный парадокс возник бы лишь в том случае, если бы Эпименид сказал: «Все критяне всегда лгут».
Давайте попробуем перефразировать Эпименида на современный лад. Представьте себе, что министр внутренних дел заявляет: «Все министры постоянно лгут». Но ведь он тоже министр, и, следовательно, его утверждение ложно, и министры постоянно говорят правду. Но и этого тоже не может быть, потому что он сам только что солгал. Как ни крути, а мысли, содержащиеся в некоторых высказываниях, не то чтобы ложны, а попросту невозможны. Разрешить такой парадокс, то есть сделать из него какой-то однозначный вывод, нельзя. Это превосходит возможности мозга. Он может только отложить его в памяти как некую загадку. Это то же самое, что знаменитая лестница Эшера. Мы знаем, что такого не бывает, тем не менее видим ее своими глазами.
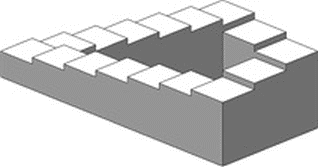
Рис. 16. Лестница Эшера
На парадоксах иногда строятся логические задачи, но чаще всего речь идет о мнимых парадоксах. Одни впадают в полный ступор, пытаясь решить красивую задачу, а вторые справляются с ней с ходу и без особого труда. Итак, перед вами фраза: «В этом предложении есть две ошипки».
Ну, первую-то вы, конечно, заметили сразу. Но как бы вы ни вычитывали каждую букву, вторую обнаружить никак не удается. Здесь всего одна орфографическая ошибка. Но кто сказал, что речь идет обязательно об орфографии? Ага, теперь поняли?
Ложь и правда – одна из излюбленных тем нашего мозга. Мы постоянно пытаемся выяснить, где правда, а где ложь. Правильно или неправильно, да или нет, точно или неточно, съедобно или ядовито, друг или враг? Сравнение и оценка – это способности, которые активизируются у человека сразу после рождения и впоследствии постоянно развиваются.
То, что даже ложь способна тренировать мозг, доказывает следующий пример. Классическая ситуация, используемая во многих логических задачах, заключается в том, что один человек всегда врет, а второй всегда говорит правду. Мы, естественно, не знаем, кто лжец, и выяснить это порой не так уж просто.
Как это сделать? Может быть, надо спросить у них, говорят ли они правду? Оба ответят утвердительно. Если спросить у одного, говорит ли другой правду, мы тоже получим одинаковый ответ. Лжец ответит: «Нет». Но то же самое скажет и любитель правды. Значит, надо придумать что-то другое. Когда придумаете, попробуйте решить следующую задачу: вы подходите к развилке дорог и встречаете на ней двоих человек, один из которых всегда лжет, а второй всегда говорит правду. Чтобы выяснить, какая дорога приведет вас в нужное место, вы имеете возможность задать им только один вопрос.
Чтобы выяснить, кто из двоих говорит неправду, надо задавать перекрестные вопросы. Это значит спрашивать одного человека о втором. Например: «Что ответит твой напарник, если я спрошу его, лжец ли он?» Тот, кто говорит неправду, ответит: «Лжец». Правдолюб ответит: «Не лжец». Отсюда можно без труда выяснить, кто говорит правду, а кто нет. Но в данной задаче вам надо с помощью одного вопроса выяснить нужное направление дороги. Думаем, что эта подсказка поможет вам найти решение.
«Это предложение неверно»
Если это предложение правдиво, значит, оно неверно. Поскольку такого быть не может, оно действительно неверно, то есть полностью соответствует своему содержанию. Таким образом, оно одновременно и правдиво, и ложно. Снова возникает противоречие.
Противоречия сопровождают нас в жизни на каждом шагу, хотя зачастую мы их не замечаем. Например, в ходе стратегического совещания, посвященного разработке нового продукта, может случиться так, что и инженеры, и маркетологи, и дизайнеры говорят об одном и том же, но имеют в виду совершенно разные вещи. Если свести все их представления воедино, получится некий продукт в авангардистском стиле, очень дешевый в производстве, отвечающий предпочтениям самых разных групп покупателей, приносящий огромную прибыль, выпускаемый в массовом порядке и занимающий на рынке элитарную нишу. Короче говоря, что-то вроде свиньи молочно-шерстяной породы, откладывающей яйца. На таких совещаниях полезно было бы поставить перед собой на стол табличку, на одной стороне которой будет написано «Все, что написано на обороте, – правда», а на другой – «Все, что написано на обороте, – неправда». Имея перед глазами такой наглядный парадокс, вы сможете легче подмечать противоречия, с которыми мы имеем дело в повседневной жизни.
Логические противоречия могут быть основанием для вполне научных выводов. С их помощью можно, например, доказать, что время течет только в одном направлении. Хорошо известен, в частности, так называемый «парадокс убитого дедушки». Предположим, существует возможность переместиться в прошлое. Некто предпринимает такое путешествие во времени, навещает в прошлом своего дедушку и убивает его еще до того, как он успел зачать своего сына (то есть отца путешественника во времени). И тут возникает проблема. Поскольку его отец не родился, значит, не мог родиться и сам путешественник. Следовательно, он не мог отправиться в прошлое, чтобы убить своего дедушку. Классический закольцованный парадокс, из которого не видно иного выхода, кроме как признать, что путешествия в прошлое невозможны.
И все же, обдумывая эту историю, вы можете дать волю своей фантазии. Вам не приходят в голову сценарии, в которых убийство дедушки в прошлом все же могло состояться? Именно этим занимаются философы и физики-теоретики, сталкиваясь с очевидными ограничениями. Мысленные эксперименты не столь доказательны, как осуществляемые в реальности, но порой указывают путь к моделям, которые можно реально построить. Возможно, существуют какие-то параллельные ответвления времени и истории. В тот момент, когда путешественник во времени оказывается в прошлом, прежнее течение времени раздваивается, образуя начало новой реальности при одновременном сохранении старой. Подобные мыслительные пируэты не только занимательны, но и тренируют воображение. Поиск путей между «возможно» и «невозможно» очень освежает мозг.
Курица или яйцо? Противоречия стимулируют мозг
Когда в конце XIX века начала приобретать популярность эволюционная теория Дарвина, одной из самых животрепещущих тем для дискуссий стал вопрос, что было раньше: курица или яйцо? Однако вопрос о происхождении кур с точки зрения современной науки уже выходит за рамки первенства курицы или яйца. Большинство ученых согласны в том, что у кур в процессе эволюции было столько предшественников, что в биологическом плане бессмысленно ставить вопрос как о первой курице, так и о первом курином яйце. Все очень понятно и элегантно. Часто, когда ученые не могут справиться с очередным парадоксом, они просто формулируют проблему несколько иначе.
Вплоть до XIX века господствующей теорией происхождения мира была Первая книга Моисеева – Бытие, в которой содержались иудейско-христианские представления о том, как появилась жизнь. Согласно ей Бог создал все виды животных, следовательно, и кур тоже. После того как первый петух потоптал первую курицу, та отложила первое яйцо, из которого появился первый цыпленок. Таким образом, Ветхий Завет предлагает второе решение проблемы курицы и яйца. Кстати, косвенное отношение к этой проблеме имеет и задача, которую мы хотим вам предложить. Как-то раз Адам работал в поле с двумя своими взрослыми сыновьями Каином и Авелем. В полдень они обнаженными легли отдохнуть в тени дерева. Рост и телосложение у всех были одинаковыми. Ева выглянула из дома и, хотя лица мужчин были скрыты тенью, безошибочно узнала своего мужа Адама. Как она отличила его от сыновей?
В последнее время все проблемы, в основе которых лежит вопрос об исходном элементе причинно-следственной цепи, где причины и следствия поочередно меняются, объединяют общим названием «проблема курицы и яйца». Схожие логические задачи на протяжении многих веков были любимыми упражнениями богословов и философов для тренировки мозга. Последователи дзен-буддизма решали, например, такие классические задачи: если ударить ладонями друг о друга, будет слышен хлопок. А какой звук будет слышен, если в движении участвует только одна рука? Хорошо известна также проблема средневековых схоластиков: сколько ангелов сможет уместиться на кончике иглы?
Хотя существование Бога невозможно ни доказать, ни опровергнуть средствами логики, до сих пор не прекращаются активные попытки логического обоснования Библии. При этом порой возникают следующие вопросы: сколько рыб мог бы поймать Ной за время своего плавания на ковчеге? Как бы вы ответили?
Бой с тенью: мнимые противоречия
Разрешение противоречий идет на пользу не только философам и физикам-теоретикам. С этим сталкивается в повседневной жизни каждый из нас. Размышления на данную тему не только интересны, но и поучительны. Они служат для тренировки мозга. Опыт, полученный в ходе таких тренировок, позволяет разрабатывать практичные стратегии для реальной жизни. В частности, он дает возможность выяснить, действительно ли мы имеем дело с противоречием. Поэтому, если шеф поручает вам разработать рекламную кампанию, которая взбудоражит все умы, но при этом должна быть тихой и незаметной, подумайте несколько раз, прежде чем обвинить его в том, что эти требования взаимно исключают друг друга. Ведь почти любое противоречие можно объяснить и использовать в своих интересах, особенно в сфере рекламы. Правда, и математика тоже не является исключением. В доказательство приведем следующую задачу.
Как известно, талер Марии Терезии – это цельная монета, у которой нет ни половинок, ни четвертинок. Тем не менее, когда директор австрийского банка задал своему служащему вопрос, сколько монет он продал за день, тот ответил:
– Первый клиент захотел купить половину имеющихся монет плюс одну половинку. Второй, оценив оставшийся запас, тоже решил купить половину монет плюс одну половинку. Третий клиент высказал такое же пожелание, после чего монет больше не осталось.
– Значит, все распродано? Поздравляю, – сказал директор. – Но, я надеюсь, вы не распиливали монеты?
– Разумеется, нет.
– Тогда я знаю, сколько их было изначально.
А вы знаете?
Задачи, подобные этой, могут довести до отчаяния, но решение можно найти довольно быстро, если не ограничивать свою мысль кажущимися парадоксами. Ведь если начать размышлять над тем, как совместить очевидно противоречащие друг другу высказывания о половинках талеров, которых на самом деле быть не может, то можно оказаться в тупике. Но противоречие здесь мнимое, так как половинки в данном случае – это лишь математическая абстракция, а не реальность.
Арабские математики, которые внесли немалый вклад в развитие этой науки, оставили нам в наследство еще один знаменитый пример парадоксального решения задачи. Один шейх, лежа на смертном одре, призвал к себе троих сыновей, чтобы огласить свою последнюю волю: «Как вы знаете, у меня есть 17 верблюдов, и я хочу разделить их между вами по старшинству. Старший сын Али получит половину верблюдов, средний сын Омар – одну треть, а младший Хаммед – одну шестую». С этими словами он умер.
А теперь попробуйте разделить 17 верблюдов в соответствии с завещанием. Впору звать мясника с ножом, потому что одна треть от 17 верблюдов – это 5,6666666… (периодическая дробь). Кроме того, мертвый верблюд, разделенный на части, не представляет такой ценности, как живой. Но тут пришел сосед, который помог братьям решить задачу по справедливости.
«От вас потребуются дополнительные затраты в размере стоимости еще одного верблюда», – сказал он. Все трое согласились и собрали нужную сумму. Сосед купил верблюда и добавил его к стаду, после чего произвел раздел: 9 верблюдов – для Али, 6 – для Омара и 3 – для Хаммеда. И никаких фокусов. Каждому досталась своя доля, а сосед радостный пошел домой, хотя и не получил ничего за свою смекалку.
Есть еще один вариант этой задачи, которую теперь вы сможете решить сами. Умирающий шейх оставляет после себя 11 верблюдов, но на этот раз у него четыре сына. Али должен получить одну треть, Омар – четверть, а два младших брата-близнеца – по одной шестой.
Решив данную задачу, вы убедитесь, что на этот раз хитрый сосед остался с неплохой прибылью. Каким образом? В отличие от первого завещания, второе скрывает в себе небольшой подвох, в связи с чем подобные задачи часто относят к категории шуточных, но для любителей головоломок это не должно быть препятствием. Ведь если задачу удается решить только с помощью какого-то фокуса, это свидетельствует о подлинном мастерстве. Подвох в данном случае заключается в том, что указанные в завещании доли в сумме не дают целой единицы. Если привести дроби к общему знаменателю, выяснится, что 11 верблюдов составляют одиннадцать двенадцатых от всего стада. Однако те, кто решает задачу, исходят из того, что умирающему шейху не до шуток и он относится к своему завещанию всерьез. Это и заводит их в тупик парадокса.
К числу мнимых проблем можно отнести и так называемый парадокс дней рождения. Здесь в общем-то нет никакого противоречия. Данный пример лишь демонстрирует нашу неспособность оценивать вероятность. Вопрос, который с успехом можно задавать на вечеринках и конференциях, звучит так: какова вероятность того, что из 23 присутствующих найдутся двое с одинаковой датой рождения? Если вы не математик, то можно с полной уверенностью утверждать, что вы ошибетесь. Вероятность составляет вовсе не 5 процентов (как чаще всего считают), а превышает 50 процентов. Если же группа состоит из 50 человек, то вероятность увеличивается до 97 процентов.
Творческому мышлению требуется свободное пространство
Одним из интересных аспектов умственных упражнений является то, что правильного решения может и не быть, если понимать «правильность» в математическом смысле. На вопрос, сколько восьмых частей содержится в единице, есть только один-единственный верный ответ. Но бывают вопросы, на которые существует множество ответов, и их нельзя однозначно отнести к категории «правильных» или «неправильных».
Искусство творческого мышления вырабатывается именно на таких вопросах, где поиск решения важнее самого решения. Каждому хорошему шахматисту известно, что порой выигранная, но неинтересная партия доставляет меньше удовольствия, чем проигранная, но полная напряжения и нестандартных ситуаций. Путь к цели доставляет больше творческих радостей, чем результат. Большинство приведенных в этой книге задач имеет только одно решение, и читатели с интересом его ищут. В то же время задача с неопределенным ответом поначалу ставит нас в тупик, хотя в жизни мы на каждом шагу сталкиваемся с проблемами, имеющими несколько решений. Например, после работы шеф решил устроить совещание и предлагает вам выступить, хотя вы к этому не готовы. К тому же вы обещали как раз в это время забрать детей с тренировки домой. Такие расплывчатые проблемы возникают чуть ли не каждый день, и большинство из них мы решаем очень быстро и без особого анализа ситуации. Дело в том, что и условие подобных задач зачастую сформулировано очень нечетко, в виде каких-то не связанных между собой заданий и требований, и мы пытаемся найти приемлемое решение в зависимости от своего характера и ситуации. Мы можем справиться с проблемой лучше или хуже, но единственного и самого правильного решения не бывает. Такова жизнь.
Насколько нечетко поставленная задача может активизировать нашу способность к творческому мышлению, хорошо демонстрирует пример с черным цилиндром. Английский психолог и консультант по вопросам менеджмента Эдвард де Боно придумал эту задачу более тридцати лет назад и получил с тех пор несколько тысяч ответов, но ни одного правильного. Дело в том, что здесь и нет правильных ответов. Они могут быть только лучше или хуже.
Этот эксперимент де Боно проводил более чем с тысячей людей. На белом столе стоит высокий черный цилиндр (имеется в виду не шляпа, а геометрическое тело). Примерно через 20 минут он внезапно падает. К цилиндру за это время никто не приближался, перед падением не было никаких звуков, в цилиндр не кидали никаких предметов и не толкали стол. Землетрясения тоже не было. К цилиндру не прикреплены никакие нити. Вы должны подумать и дать ответ, почему он упал. Для этого у вас есть 10 минут.
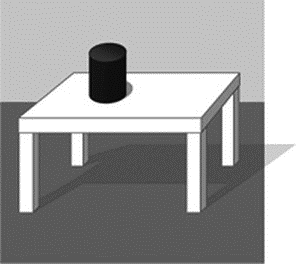
Рис. 17. Черный цилиндр
Попробуйте решить эту задачу прямо сейчас. Отложите книгу в сторону и подумайте. Можете взять лист бумаги и карандаш, потому что вам может понадобиться нарисовать схему. Посвятите этому заданию 10 минут, а потом продолжайте читать дальше.
Вы плодотворно провели это время? Пришли к какому-нибудь удовлетворительному решению? Каким бы оно ни было, вам пришлось сражаться с теми же трудностями, что и другим читателям. У вас было слишком мало информации. Какова величина цилиндра? Из какого материала он сделан? Какова температура в комнате? Вам некого об этом спросить, а значит, данные, с которыми приходится работать, создаются у вас в голове. Вы мысленно воссоздаете и стол, и сам цилиндр, и механизм, который заставляет его опрокинуться. Вот это и есть творческое мышление.
Эдвард де Боно уже много десятилетий назад предостерегал, что не стоит отводить слишком значимое место логическому мышлению, как это традиционно принято на Западе. По его мнению, в том, что совершенство логических построений вызывает у человека ложное чувство превосходства и собственной правоты, кроется большая опасность. Логическое обоснование признается единственно правильным, поэтому люди на Западе с недоверием относятся к новым и поражающим воображение решениям. Они подавляют в себе легкость и свободу мышления, хотя известно, что самые крупные открытия являются результатом проявления интуиции, спонтанности, а также хаоса и сомнений в аксиомах. Здесь требуется сочетание игры мыслей и логического контроля над ними.
Для того чтобы прийти к удовлетворительному решению расплывчатой задачи (имеется в виду не нечеткость поставленного вопроса, а недостаток имеющейся в распоряжении информации), необходимо прибегнуть к приемам, которые практически не используются в решении технических проблем, – латеральному мышлению, фантазии и юмору. Эта мысленная акробатика должна восприниматься как тренировка. Вы должны мыслить свободно и необычно. Допускайте любую, даже самую абсурдную возможность, а затем контролируйте полученные выводы с помощью строгой и беспощадной логики. Не довольствуйтесь единственным решением. Всегда ищите второе или альтернативное. Обсуждайте их с друзьями и коллегами.
Кто бреет цирюльника, если он не бреется сам?
Этот парадокс был сформулирован математиком Бертраном Расселом: «Севильский цирюльник бреет всех мужчин в Севилье, за исключением тех, кто бреется сам. Но если так, то бреет ли себя севильский цирюльник?» Мы исходим из того, что он не отпускает бороду, так как предлагаемая задача не относится к категории шуточных.
Из условия следует, что если он не бреет себя сам, то бреется сам (такого, естественно, быть не может). Если он бреется сам, то, значит, не может себя брить (это тоже невозможно). Одно сплошное противоречие. Таким образом, следует признать невозможным само условие задачи. На первый взгляд оно сформулировано разумно и логично, но при ближайшем рассмотрении оказывается парадоксом.
Проблема данного парадокса заключается в том, что он начинается с ложной посылки. Само допущение, что такой цирюльник может существовать, уже ложно. Это все равно что утверждать: «Цирюльник одновременно жив и мертв». В математике это называется доказательством от обратного. Мы делаем некое предположение и приходим к выводу о его противоречивости. Это доказывает ложность предположения, что существование такого цирюльника возможно.
Отсюда вытекает первое правило решения логических задач: «Для начала проанализируй постановку вопроса!»
● Достаточно ли подробно он сформулирован?
● Содержит ли он полную информацию?
● Нет ли в нем скрытых противоречий?
● Выполнимы ли в принципе условия, изложенные в вопросе?
В повседневной жизни это означает, что прежде, чем приступить к решению проблемы, необходимо тщательно проверить условие. Это позволяет избежать ненужной работы, а также оградить себя от всяких бездельников и шарлатанов, которые крадут у вас драгоценное время или пытаются всучить что-то бесполезное.
Веселые парадоксы
Парадоксы могут заставить смеяться, и лучше всего это доказывают ученые, не относящиеся к числу обладающих развитым чувством юмора, – статистики. Так называемый феномен Уилла Роджерса является следствием формирования усредненных данных по тем или иным группам: при перемещении элементов из одной группы в другую средние значения могут повышаться в обеих группах, даже если индивидуальные показатели при этом ухудшаются (или наоборот). Если вам все еще не смешно, значит, вы пока не осознали всех последствий этого приема, который статистики называют «злонамеренным манипулированием данными». Человек, чьим именем назван этот феномен, был не статистиком, а комиком. Ему принадлежит фраза «При переселении жителей Оклахомы в Калифорнию повышается средний уровень интеллекта в обоих штатах».
Парадоксальные вопросы: с какого момента кучу можно называть кучей?
На вопрос «Когда мужчина становится мужчиной?» ответить ничуть не легче, чем на вопрос, начиная с какого объема куча может именоваться кучей. Хотя сам по себе вопрос кажется простым, при ближайшем рассмотрении этот парадокс кучи, приписываемый Зенону Элейскому, заставляет задуматься.
«Пятьдесят зерен пшеницы составляют кучку. Если убрать одно зерно, остается 49, которые по-прежнему являются кучкой. Продолжая убирать зерно за зерном, мы доходим до двух зерен, которые также составляют кучку». Такое положение можно по праву считать парадоксальным. Образует ли одно зерно кучку? Если нет, значит, граница между кучкой и некучкой проходит между одним зерном и двумя. Но любители логики строят на этом допущении элегантный вывод, который, в частности, утверждает, что куча существовать вообще не может.
Они доказывают это с помощью так называемой полной индукции, соединяя между собой две аксиомы:
● Одно зерно – не кучка.
● Добавляя второе зерно, которое также кучкой не является, невозможно создать кучку.
Отсюда следует, что существование кучи вообще невозможно, сколько бы зерен ни добавлялось. Но парадокс в том, что мы прекрасно знаем: кучи существуют.
Конечно, такие мнимые парадоксы легко разрешаются, потому что в их основе лежит смешение математических и общеупотребительных формулировок. Если бы математику нужно было иметь дело с понятием «куча», он предварительно дал бы ей определение, например: «Кучей является количество однородных предметов х, равное или превышающее 44х». Таким образом, перед ним даже не стоял бы вопрос, являются ли 43 зерна кучей. С математической точки зрения, безусловно, нет. Но если подходить к вопросу с позиций общеупотребительного значения слова «куча», то 30 тысяч зерен, аккуратно разложенных в один слой, для нас кучей не являются, а для математика – вполне.
Но самое забавное начинается, когда мы пытаемся развить эту мысль. Когда лес становится лесом? Когда овечье стадо становится стадом? Когда дом становится домом? Хотя дом представляет собой некоторое количество уложенных соответствующим образом кирпичей, два кирпича – это еще не дом. И три тоже нет. Тогда попробуем подойти с другой стороны. Когда дом перестает быть домом? Ведь на пути от дома к одному кирпичу есть определенные стадии: подведенная под крышу коробка, стена и т. д.
Размышления о том, что целое больше, чем сумма составляющих его частей, вновь возвращают нас к мозгу. Ведь мозг не перестает быть мозгом, если удалить из него несколько нейронов. Он не является суммой составляющих его элементов, а представляет собой сложное образование, в котором организация играет более важную роль, чем количество и свойства компонентов.
Из этих парадоксов можно извлечь важные уроки для повседневной профессиональной и личной жизни. Например, неразрешимые проблемы часто возникают из-за того, что люди говорят на разных языках. Нет, речь идет не об иностранных языках, а о разных социальных коммуникационных системах. Если муж улаживает разногласия со своей женой в том же духе, в котором решает проблемы у себя в офисе, может возникнуть парадокс. «Ты постоянно всюду опаздываешь. Научись, наконец, распоряжаться своим временем, иначе в наших отношениях может наступить разлад». И дело здесь не в том, что претензия изложена канцелярским языком, а в том, что муж рассматривает семью как некую фирму, которая должна работать по установленным правилам.
Парадоксальное и латеральное мышление
Дилеммы и парадоксы – отличная пища для мозга. Неразрешимые на первый взгляд проблемы и нелогичные взаимосвязи (которые мы тем не менее воспринимаем как реальность) стимулируют свободное латеральное мышление. Понятие латерального (или бокового) мышления было введено в обиход уже известным нам Эдвардом де Боно в 1967 году. В научной среде такой тип мышления предпочитают называть дивергентным или нелинейным. Кроме того, де Боно принадлежит также понятие «параллельное мышление», которое отражает способность систематически использовать различные подходы и точки зрения при рассмотрении любой темы.
В отличие от вертикального мышления, которое предполагает последовательное обдумывание вопроса шаг за шагом на основании привычных моделей, латеральному мышлению присущи следующие признаки:
● вся поступающая информация оценивается субъективно и используется избирательно;
● детали воспринимаются не аналитически, а интуитивно;
● ассоциации и отвлечение на смежные темы не только допускаются, но и приветствуются;
● не каждый промежуточный результат является правильным;
● решения могут быть размытыми, то есть не носящими категоричного характера (или – или, да – нет);
● даже решения, которые невозможно реализовать, считаются шагом к лучшему пониманию проблемы;
● традиционные модели решения подвергаются сомнению и предпочтение отдается необычным подходам;
● исходная ситуация и рамочные условия не считаются чем-то раз и навсегда определенным.
Тому, кому присуще латеральное мышление, решить приведенную ниже задачу будет легче, чем приверженцу строгой логики. Сколько матчей надо провести, чтобы определить победителя в турнире на выбывание, в котором участвуют 128 игроков? Логик рассуждает так: в первом круге проводится 64 игры, во втором – 32 игры, в третьем – 16, в четвертом – 8, в пятом – 4, затем еще 2 игры и финал. В сумме получается 127 игр.
Латеральное мышление предполагает совершенно иной подход без лишних подсчетов. Если в турнире участвует 128 человек, а побеждает только один, значит, должно быть 127 проигравших. Каждый из них проигрывает только один раз. Следовательно, столько же должно быть и матчей.
Оба метода приводят к одному и тому же результату, но разными путями. Латеральное мышление позволяет прийти к цели значительно быстрее и изящнее.
Любимые задачи на латеральное мышление
● Две обезьяны смотрят в трубу, лежащую на земле. Труба прямая, не очень длинная и ничем не забитая. Тем не менее обезьяны не видят друг друга. Почему?
● У господина Майера, живущего в многоквартирном доме, вечером вдруг выключается свет. Он спускается в подвал, чтобы осмотреть предохранитель, но подвальная дверь внезапно защелкивается. Открыть ее изнутри невозможно. Дверь слишком толстая, поэтому стучать и кричать бесполезно. Тем не менее ему удается позвать на помощь. Каким образом?
● Посетитель ресторана обнаруживает в своей чашке кофе муху и зовет официанта. Тот забирает чашку и через некоторое время приносит новую. Но клиент недоволен и обвиняет официанта в том, что тот просто выбросил муху вместо того, чтобы налить свежий кофе. Как он это определил?
● Два шахматиста сыграли пять партий. Количество выигрышей и проигрышей у обоих оказалось одинаковым, хотя ни в одной из партий не была зафиксирована ничья. Как такое возможно?
● Два человека побывали на экскурсии в угольной шахте. Когда они оттуда вышли, у одного было чистое лицо, а у другого – грязное. Человек с чистым лицом сразу пошел умываться, а с грязным – нет. Почему?
● Пятерых человек по пути застал дождь. Четверо ускорили шаг, а пятый не обратил на дождь никакого внимания. Тем не менее все прибыли к месту назначения одновременно, причем четверо промокли, а пятый остался сухим. Каким образом?
Кроме задач на латеральное мышление, которые можно решить, только отвлекшись от привычной логической модели мышления, существуют еще латеральные загадки (или загадки-расследования), в которых даются лишь фрагменты информации, складывающиеся, казалось бы, в абсурдную ситуацию. Разгадывающему предстоит обнаружить в ней смысл. Ведущий, которому известна суть истории, рассказывает загадку, а игроки задают уточняющие вопросы, на которые можно ответить только «да» или «нет». Чтобы вы могли получить представление о том, как выглядят такие загадки, мы приводим здесь несколько наиболее известных. С их помощью вы можете развлечь членов семьи или друзей на вечеринке.
Итак, у вас имеется следующая информация: мертвые Ромео и Джульетта лежат на полу у открытого окна. На мокром полу повсюду разбросаны осколки стекла. Что произошло?
Ответ таков: Ромео и Джульетта – это имена аквариумных рыбок. Из-за сквозняка распахнулось окно, столкнувшее аквариум на пол. Аквариум разбился, и рыбки задохнулись.
А теперь испытайте свои силы на следующих загадках:
● На снегу лежит труп голого человека. В руке у него зажата спичка. Поблизости не видно никаких следов. Что произошло?
● Мертвый человек сидит в помещении на стуле перед шахматной доской, на которой расставлена проигранная им партия. В руке у него пистолет. Что произошло?
● Грабитель оказался в здании. Хотя оно хорошо охраняется, ему удалось попасть туда без всяких проблем. Он находился в этом здании долгое время, а затем вышел, вновь не вызвав никакой тревоги. Но если бы он попытался выйти раньше, то был бы схвачен. Где он находился?
● Слон стоит на поле. В этот момент к нему подходит конь, после чего слон бесследно исчезает. Как такое может быть?
● Мужчина смотрит в окно и видит красивую женщину, проходящую возле его дома. Вскоре после этого он умирает. Если бы он не увидел эту женщину, то был бы жив. Из окна он не выпадал. Что произошло?
● Более двадцати музыкантов симфонического оркестра играют для публики, но их никто не слушает. Почему?
● Фриц купил себе диск с записью нового фильма. Придя домой, он решил сразу же посмотреть диск вместе с Францем. Но Франц уже через несколько секунд сказал, что конец фильма им посмотреть не удастся, так как запись повреждена. Каким образом Франц выяснил это так быстро?
● Господин Майер ехал на автомобиле по дороге с односторонним движением и внезапно столкнулся со встречной машиной. Во время аварии он получил лишь легкие повреждения. Водитель, нарушивший правила движения, оказался зажат в своей машине, и его удалось высвободить только через несколько часов. Тем не менее он выжил. Хотя в столкновении участвовало только два автомобиля и ни в одном из них не было пассажиров, один человек во время аварии все же погиб. Кто он?
Назад: Ошибки мышления
Дальше: Логическое мышление

