Здравый смысл – трудно определимое понятие. И к тому же опасное. Так, например, человек, озабоченный глобальным потеплением, приходит к выводу, что необходимо что-то предпринять. Он продает свой автомобиль, но при этом продолжает летать в отпуск из Европы в Австралию. И это отнюдь не противоречит его здравому смыслу: самолет ведь все равно полетит туда даже без него. С точки зрения экологического баланса это катастрофа, но здравый рассудок отказывается это понимать. Он вообще легко впадает в заблуждение, и применение к нему прилагательного «здравый» вызывает большие сомнения. Опаснее его может быть только «здоровое национальное сознание». Но давайте все же разберемся, как функционирует этот здравый смысл и почему он так часто ошибается.

Представьте себе, что президент некой страны, начитавшийся в молодости Маркса, решает по справедливости перераспределить богатство среди своего народа. Он не хочет ни революций, ни налоговых реформ, поэтому придумывает нечто совершенно новое. Он делит все население на пять классов: бедные, нуждающиеся, средний класс, зажиточные и богатые. Затем между двумя соседними классами поочередно уравниваются доходы. План предусматривает, что сначала усредняются доходы бедных и нуждающихся (их доходы складываются, а затем делятся поровну). Затем то же самое происходит между нуждающимися и средним классом, между средним классом и зажиточными и, наконец, между зажиточными и богатыми. Но богачи считают, что они при этом будут ущемлены, и предлагают начать перераспределение сверху, то есть сначала усредняются доходы между богатыми и зажиточными, потом между зажиточными и средним классом и так далее вплоть до бедняков. Как ни странно, это предложение находит всеобщую поддержку. А что вам подсказывает здравый рассудок? Как вы отнеслись бы к этому плану с обеих позиций, то есть с точки зрениях бедных и богатых?

Здравый смысл вмешивается даже в те области, где ему совершенно нечего делать, например в математику. Давайте предположим, что Земля – идеальный шар с гладкой поверхностью без возвышенностей и впадин и протяженность ее экватора составляет ровно 40 тысяч километров. Мы натягиваем шнур по экватору вокруг всего земного шара. Его длина должна тоже составлять 40 тысяч километров, но, к сожалению, он оказывается на 1 метр длиннее – 40 000,001 километра. Возможно, тот, кто отмерял этот шнур, решил, что один лишний метр по сравнению с длиной экватора абсолютно ничего не значит, так как эти величины несопоставимы. Теперь представьте себе, что этот шнур висит над экватором, образуя по всей длине равномерный зазор (он ведь длиннее, чем надо). Каким будет этот зазор? Несколько микронов? Миллиметр? Пара сантиметров? Прикиньте сами. А теперь представьте себе, что вы натянули шнур вокруг шара для боулинга, а потом удлинили его на 1 метр. Каким теперь будет зазор между шнуром и шаром? Ну, это-то вы можете себе представить!

И тут для здравого смысла наступает шок. Оказывается, если удлинить шнур на 1 метр, зазор будет всегда одинаковым независимо от того, идет ли речь о земном шаре или шаре для боулинга, а именно около 16 сантиметров.

Таким образом, на здравый смысл надо полагаться с большой осторожностью. С его помощью можно решать лишь несложные вопросы, но, когда мы сталкиваемся со сложными или хитро сформулированными задачами, здравый смысл является слишком грубым инструментом. Для того чтобы наглядно и объемно представить себе сложный и постоянно меняющийся процесс, а также его возможный результат, требуется значительное интеллектуальное усилие, но подобные упражнения прекрасно тренируют мозг. Проверьте себя, решив следующую задачу.

Самолет летит из Берлина в Рим, а затем возвращается обратно. Все это время довольно сильный ветер дует прямо в направлении Рим – Берлин. Совершенно очевидно, что попутный ветер ускоряет полет, а встречный замедляет. А теперь сравните эту ситуацию с той, когда на протяжении всего маршрута туда и обратно царит полное безветрие. Будет ли суммарное время полета в обоих случаях одинаковым? Если да, то почему?

Видите, какую осторожность надо соблюдать в подобных вопросах? Первый спонтанный ответ кажется вполне «логичным», но он необязательно верен. А вот вам еще один вопрос, на который каждый готов дать ответ, не задумываясь. Но насколько он правилен?

В семье двое детей, один из которых мальчик. Какова вероятность того, что другой ребенок тоже мальчик?

Наш мозг отказывается верить, потому что у него слабо развита способность к абстрактным представлениям. Порой такое трудно представить себе даже математикам, но они знают, что это так и есть, поскольку расчеты не врут. Математики знают, что существует бесконечное количество целых чисел. Но им также известно, что существует такое же количество четных чисел, хотя здравый смысл подсказывает, что их должно быть вдвое меньше. А есть еще так называемые простые числа, которые делятся только на единицу и сами на себя. Они пока найдены не все. Наибольшее из известных нам на сегодняшний день простых чисел – это 2^32582657 – 1. Суперкомпьютеры работают день и ночь, чтобы найти следующее, потому что мы знаем, что таких чисел тоже должно быть бесконечное количество. Может ли осознать это «здравый смысл»? Едва ли. В это надо просто верить. Математика может с легкостью ввести в заблуждение наш слишком конкретно мыслящий мозг. Но хуже всего то, что, даже когда математика нам все объяснила и доказала, мы все равно продолжаем верить своим органам чувств.

Возьмем для примера обычную полоску бумаги. У нее есть верхняя и нижняя поверхность, а также два края по бокам. Напишите на ней сверху А, а снизу Б. Вы ничуть не сомневаетесь, что буквы находятся на разных сторонах полоски. Вы можете в этом поклясться и даже поспорить на крупную сумму. Но вот этого лучше не делать. Любой математик с легкостью докажет вам, что обе буквы находятся на одной стороне и что у этой полосы бумаги вообще только одна поверхность. Это делается так: один конец полоски поворачивается на 180 градусов и склеивается со вторым. У вас получился невозможный объект. Если вы из любой точки полоски проведете карандашом линию параллельно краю, то вернетесь к той же самой точке, не переворачивая полоску на другую сторону, причем карандашный след останется с обеих сторон ленты. Все потому, что у этой ленты на самом деле только одна сторона.

Рис. 10. Лента Мёбиуса

Лента Мёбиуса (названная так по имени математика Августа Фердинанда Мёбиуса, открывшего этот феномен в 1858 году) представляет собой «объект, замыкающийся сам на себя». Это значит, что вы держите в руке то, чего, вообще-то, не может существовать: двухмерный объект в трехмерном пространстве. Разумеется, математики давно описали и классифицировали этот феномен. Они называют его неориентируемой поверхностью, хотя неспециалисту это ни о чем не говорит и ничего не объясняет. Тем не менее это ничуть не умаляет чуда, сотворенного из обычной бумажной полоски. Особенно интересно, как наш мозг реагирует на «то, чего не может быть». Ведь в школе нас учили, что мы существуем в четырехмерном пространственно-временном континууме, в котором не может быть ничего двухмерного. Таким образом, существуют границы, за которыми наше мышление просто отказывает. Навигатор в мозге теряет связь со спутником, и мысли разбредаются в разных направлениях по неизведанной местности. Похоже, что в мозге предусмотрена некая аварийная программа для явлений, которые мы наблюдаем, но не можем осознать и объяснить. Это можно сказать, в частности, об оптических иллюзиях, которые нас одновременно завораживают и сбивают с толку, поскольку в них что-то «не сходится». Оптические иллюзии – это изображения, которые глаз способен воспринять, но мозг не в состоянии понять и объяснить. Такой обман восприятия основывается на самых разных эффектах: на остаточном изображении на сетчатке глаза, на отвлечении внимания, на контрасте и цвете, на свете и тени, на наших устоявшихся приемах получения зрительной информации. Во всех случаях зрение нас обманывает, что можно легко доказать, прибегнув к помощи других органов чувств. Взгляните на рисунок 11. Вам потребуется некоторое время, чтобы расшифровать текст. И дело тут не только в том, что он написан по-английски.

Рис. 11. Загадочная надпись

На рисунке 12, представляющем собой одновременно и оптическую иллюзию, и задачу по комбинаторике, мы имеем дело совершенно с другим явлением. Изображенные здесь знаки не являются буквами какого-то языка. Они понятны всем в мире, и вы их, конечно, тоже знаете. Вы видите их каждый день, пишете их, думаете о них, а время от времени и проклинаете. Но если так, вам не составит никакого труда дописать пятый знак из этого ряда.

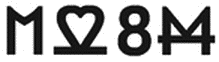
Рис. 12. Странные знаки

Оптических иллюзий всякого рода очень много, потому что нет ничего легче, чем обмануть зрение. Но особый шик заключается в том, чтобы обмануть мозг. Взгляните на рисунок 13. Обе фигуры состоят из одних и тех же частей, но нижняя почему-то оказывается на целый квадратик больше. Как такое может быть? Мы не хотим, чтобы вы сломали себе мозг, поэтому сразу раскроем секрет. Несмотря на кажущуюся тождественность, острые углы треугольников, из которых состоит фигура, не одинаковы. Поэтому ее верхняя сторона в одном случае едва заметно изогнута вниз, а в другом – вверх. Образующаяся за счет этого разница площади и составляет тот самый квадратик.

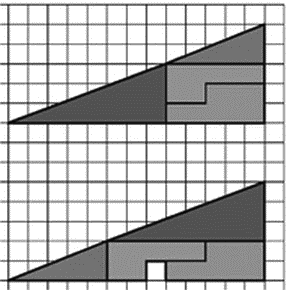
Рис. 13. Задача с треугольниками

Голландский художник и график М. К. Эшер вдохновенно изображал миры, которых не может существовать. Он занимался не столько иллюзиями, сколько геометрической фантастикой. Он создал знаменитую бесконечную лестницу, рептилий, словно выползающих из плоскости рисунка и вновь скрывающихся в ней. Для его картин характерны невероятные метаморфозы и перспективы. В отличие от обычных оптических иллюзий, обманывающих систему зрительного восприятия, он с помощью своих картин обращался непосредственно к мозгу. Разумеется, в трехмерном пространстве невозможно построить лестницу, которая начинается там же, где и заканчивается. Но на двухмерном изображении это вполне возможно. Если же в качестве инструмента воспользоваться своими особенностями зрительного восприятия, мы будем, словно малые дети, неотрывно следить глазами за монахами, спускающимися и поднимающимися по этой лестнице.

Рис. 14. «Вверх и вниз по лестнице». М. К. Эшер. Литография. 1960 год

Вы можете своими руками создать подобную иллюзию для мозга и тем самым активизировать нейроны участников нудного совещания или вечеринки. Сложите квадратный лист бумаги пополам и сделайте на нем три прямых надреза ножницами, чтобы получить изображенную на рисунке фигуру, которая на первый взгляд кажется невозможной. Как это сделать? Учтите, что полностью разрезать, а потом склеивать бумагу нельзя.

Рис. 15. Невозможная фигура

Когда мы что-то прикидываем на глазок, порой можно услышать такое выражение: «Пи, умноженное на длину большого пальца». Если число π мы еще худо-бедно знаем вплоть до четвертого-пятого знака после запятой, то большой палец у всех разный. И все же люди с учетом их ограниченных возможностей на удивление хорошо способны на глазок оценивать различные параметры. Если перед взрослым человеком положить деревянную рейку длиной с руку и попросить отметить середину, он в 90 процентах случаев сделает это с точностью до 2 сантиметров. Если дать ему пакет сахара, он почти всегда точно скажет, весит ли он больше или меньше 500 граммов. Мы достаточно хорошо определяем на глаз расстояния до 30 метров, можем примерно сказать, который сейчас час, и варим макароны, не глядя на секундомер. Эти способности можно развить с помощью тренировки. Опытный архитектор способен достаточно точно определить высоту здания, маляр навскидку скажет вам площадь стен в квартире, а лесник – объем сваленного дерева в кубометрах. Но речь здесь идет лишь о развитии функций выживания древнего человека на основании опыта. Во всех остальных случаях умножение π на большой палец приведет к неудаче.

Вам нужен пример? Пожалуйста. 28 августа 888 года в летописях было впервые упомянуто селение Нойндорф в горах Айфель, основанное еще римлянами. Самое замечательное в этой дате то, что она состоит только из четных цифр: 28.8.888. А теперь прикиньте (но только на глаз, без подсчетов!), сколько дней, месяцев или лет прошло до следующей даты, состоящей только из четных цифр?

Все, что можно взять в руку, мы оцениваем достаточно безошибочно. Но что можно сказать о таком объекте, как, например, Эйфелева башня? Попробуйте примерно сказать, сколько она весит: 8, 80, 800 или 8000 тонн? Ну хорошо, с этим вы справились. Высота Эйфелевой башни – 300 метров, а вес действительно 8000 тонн. А теперь представьте себе, что из того же материала изготовлена точная копия, уменьшенная в тысячу раз. Ее высота – 30 сантиметров. А сколько она весит? 8 граммов, 80 граммов, 800 граммов, 8 килограммов или 80 килограммов?

Потренировав свой здравый смысл, вы сможете с большей точностью оценивать вес. Попробуйте сделать это, выслушав современную сказку. Бедный подмастерье мельника, закончив учебу, получил в качестве оплаты только гуся. Он пожаловался:

– Раньше подмастерья получали более ценные вещи вроде волшебного горшочка, скатерти-самобранки или шапки-невидимки. А что сегодня? Какой-то несчастный гусь!

– Он как-никак 6 кило весит, – невозмутимо ответил мельник. – Если тебе не нравится, сходи в лес к фее, пусть она сделает этого гуся золотым.

Подмастерье так и сделал. Он пошел к фее, и та исполнила его желание. Перед ним вдруг оказался слиток золота размером с гуся. «Я миллионер!» – радостно воскликнул подмастерье, схватил гуся под мышку и помчался домой. Как вы считаете, что в этой сказке не соответствует действительности (естественно, за исключением того, что феи в наши дни не водятся)?

Еще одна тема, где люди часто допускают промашку, – это деньги. Нормальный человеческий рассудок не справляется с большинством денежных операций, и именно за счет этого живут банки, страховые и лизинговые компании. Банкиры знают, какой разрушительный эффект могут оказать проценты по кредиту, но им также хорошо известно, какие доходы приносят сложные проценты по вкладу. Если вы положили на счет 100 евро под 3 процента годовых, то через год у вас будет 103 евро. Вы оставляете эти деньги на счете, и в следующем году у вас уже 106,09 евро. Казалось бы, мелочь, но со временем доходы начинают прирастать с головокружительной скоростью.

Что такое экспоненциальный рост, можно наглядно продемонстрировать на примере, который также превосходит возможности здравого рассудка. Предположим, в 7 году нашей эры уже работал банк, в который наш далекий предок положил золотой шарик диаметром 1 миллиметр под вполне реальные 3,5 процента годовых. Никто из его потомков не добавлял туда больше ни копейки. Весь прирост осуществлялся только за счет процентов. Поскольку нам трудно судить о том, как на протяжении веков менялись цены на золото, предположим для простоты, что шарик просто рос в объеме в соответствии с оговоренными процентами. В результате этот шарик, имевший первоначально диаметр 1 миллиметр, вырос бы к сегодняшнему дню до 12 600 километров. Это значит, что мы стали бы обладателями золотого шара размером почти с Землю. Из этого примера можно сделать два вывода: во-первых, таких длительных вкладов не существует, а во-вторых, наш здравый смысл имеет мало общего с денежными операциями.

Что вы скажете о следующей финансовой операции: вы берете у друга взаймы 1000 евро и договариваетесь, что будете возвращать долг частями каждый месяц. В первый месяц 500 евро, во второй – 250 и так далее, каждый раз уменьшая сумму вдвое. Когда вы полностью выплатите долг? Разумеется, никогда, потому что всегда будет какой-то остаток. Впору вспомнить о беге наперегонки Ахилла и черепахи.

Как видите, здравый смысл частенько нас подводит. Прочитайте, пожалуйста, следующие двенадцать утверждений и быстро оцените, какие из них соответствуют действительности, а какие – нет.

● Стандартный мяч для гольфа имеет на поверхности 336 углублений.

● Жираф может обходиться без воды дольше, чем верблюд.

● Организм взрослого человека, занимающегося тяжелым физическим трудом, выделяет за день с потом до 15 литров воды.

● Большой реактивный авиалайнер расходует при взлете свыше 15 тысяч литров топлива.

● Акула может учуять запах крови при ее концентрации в воде 1:100 000 000.

● В соответствии с английским законом от 1845 года попытка самоубийства считалась тяжким преступлением и каралась смертной казнью через повешение.

● Нюх у собаки в 20 раз чувствительнее, чем у человека.

● На Земле живет примерно столько же кур, сколько и людей.

● Если куклу Барби увеличить до нормального человеческого роста, обхват ее бюста, талии и бедер составит 100-59-84.

● Луна имеет такой же объем, как Тихий океан.

● Глаз страуса по размеру больше, чем его мозг.

● У тигров полосатую окраску имеет не только шерсть, но и кожа под ней.

Как известно, в зеркальном отражении меняются местами правая и левая стороны. Но если так, то зеркало должно менять не только левую сторону с правой, но и верх с низом. Однако этого не происходит. Почему?

На самом деле мы сильно заблуждаемся, когда считаем, что левая и правая стороны в отражении меняются. В действительности зеркало меняет местами не правую и левую стороны, а переднюю и заднюю. То, что находится слева от зеркала, мы и видим слева, а то, что находится справа, отражается тоже справа, вот только нам кажется, что предметы находятся не перед зеркалом, а за ним. Когда мы смотрим на отражение предмета в зеркале, нам кажется, что наш взгляд направлен в сторону зеркала. На самом же деле мы видим этот предмет с противоположного направления, то есть со стороны зеркала.

Тот же самый эффект создается, когда мы пишем какой-то текст на прозрачной пленке, а затем смотрим на него с обратной стороны. Мы видим как бы зеркальное отражение текста, но ведь в данном случае мы меняли местами не левую и правую стороны, а переднюю и заднюю. Кстати, зеркало может менять местами и верх с низом. Для этого его надо положить на пол. В этом случае передняя и задняя стороны будут соответствовать верху и низу. Глядя вниз, мы увидим потолок.

Но сейчас мы хотим поговорить о зеркальном отражении мышления. Мы смотрим на какую-то задачу, которая на первый взгляд сформулирована ясно и просто, и не замечаем, что нас пытаются одурачить, подсовывая зеркальное отражение логики и затемняя ясность мышления, например:

Человек стоит перед портретом. Его спрашивают: «Кто изображен на портрете, который вы так внимательно рассматриваете?» Он отвечает: «У меня нет братьев и сестер, но отец изображенного человека – это сын моего отца». На чей портрет он смотрит?

Как ни странно, большинство людей отвечают неправильно, считая, что он смотрит на свой собственный портрет. Они ставят себя на его место и приводят следующие аргументы: «Поскольку у меня нет братьев и сестер, значит, сын моего отца – это я сам. Поэтому я смотрю на свой портрет».

Первая часть этого аргумента абсолютно верна. Если у человека нет братьев и сестер, значит, он и в самом деле сын своего отца. Однако из этого вовсе не следует, что именно он изображен на портрете. Если бы вторая часть фразы звучала так: «Изображенный человек – сын моего отца», то ответ был бы правильным. Но условие изложено иначе: «Отец изображенного человека – это сын моего отца». Из этого следует, что «я сам» относится к отцу изображенного человека, то есть тот, кто смотрит на портрет, видит своего сына.

Если кое-кто из скептически настроенных читателей все еще не убедился в этом (а таких окажется немало), мы постараемся ему помочь, решая задачу шаг за шагом: 1. Отец изображенного человека – сын моего отца. Давайте теперь заменим «сын моего отца» на «я сам». 2. Отец изображенного человека – это я сам. Теперь убедились?

Вопросы, сформулированные подобным образом, затемняют смысл, словно солнечные очки. Кстати, на этот счет тоже есть задача, которая простотой своей формулировки сбивает слушателя с толку. Вы покупаете солнечные очки с затемненными стеклами, но не обладающие защитой от ультрафиолетовых лучей. Как это скажется на ваших глазах?

●  В прошлый раз, когда у этого известного нейрофизиолога был день рождения, ему исполнилось 56 лет. – Значит, следующий день рождения он будет праздновать, когда ему будет 57 лет? – Нет. – Он что, умер? – Нет. Как такое может быть?

● Книжный червь добрался до своего любимого деликатеса – многотомного толкового словаря. Тома стоят на книжной полке в алфавитном порядке слева направо. Книжный червь прогрызает книги в строго горизонтальном направлении. Утром он начинает с первой страницы первого тома, а вечером заканчивает на последней странице второго тома. Сколько сантиметров он прогрыз? Толщина всех страниц одного тома составляет 6 сантиметров, а толщина обложки – 1 сантиметр.

● Каждый час из аэропорта Франкфурта отправляется самолет в Нью-Йорк. Точно так же каждый час из Нью-Йорка вылетает самолет в направлении Франкфурта. Полет длится десять часов. Сколько встречных самолетов вы увидите за это время?

Теперь, когда вы уже знаете, что здравый рассудок имеет мало общего с логикой, мы хотим показать вам, в каких еще лабиринтах можно запутаться. Ведь если кто-то говорит: «Логично, не правда ли?» – это отражает лишь его собственную логику, его индивидуальную систему мышления. Можно только представить себе, в какой растерянности оказывается мозг среднестатистического человека, сталкиваясь с теорией игр, представляющей собой сочетание логики, азартной игры, экономики и высшей математики. С помощью этой «логики безумия» можно предсказывать биржевые тенденции и разрабатывать лучшие покерные стратегии. На базе порой абсолютно «нелогичных» закономерностей этой теории можно создавать увлекательные игры, которые дадут возможность не только повеселиться, но и вытянуть деньги из чужих карманов. Вы считаете, что это лишь теория? Ничего подобного.

Людям, которые хотят прослыть душой компании и вдобавок кое-что подзаработать, мы можем дать совет: выставьте на аукцион банкноту в 10 евро! Вы считаете, что это идиотская затея и никто не будет покупать деньги на аукционе? Ошибаетесь. Правила просты: начальная ставка составляет 50 евроцентов, добавлять к предыдущей ставке можно не менее 50 евроцентов. Лучше всего, если в игре участвует не менее шести человек. Чем больше, тем лучше. Перед тем как начать принимать ставки, объявите об одном особенном дополнении к правилам (которое, собственно говоря, и является демонстрацией коварной природы теории игр): платить должен не только тот, кто победил в аукционе, но и тот, кто сделал предпоследнюю ставку. Конечно, теоретически можно выиграть 10 евро, уплатив всего 1. Но только теоретически, потому что при достаточном количестве участников всегда найдутся желающие поторговаться, которые не согласны сдаваться просто так. Особенно это касается предпоследнего участника, которому придется платить ни за что. Он, скорее всего, будет наращивать ставки.

1. Завязка. Задача устроителя аукциона заключается в том, чтобы разжечь в людях жадность и желание приобрести что-то задешево. «Кто хочет за 1 евро приобрести 10 евро? Начальная цена – 50 центов. Кто добавит еще 50? Выигрыш – девять к одному!» Стоит только паре человек повысить цену, дальше все пойдет как по маслу – вплоть до следующей критической фазы.

2. Середина игры. Когда ставки дойдут до 5 евро, кое-кто из участников начинает понимать, что при следующем повышении до 5,5 евро устроитель аукциона уже окажется в выигрыше. Но здесь срабатывает эгоизм. Ведь следующий участник так или иначе обеспечивает себе выгодную сделку. Плохо только тому, кто окажется предпоследним, потому что ему придется платить ни за что. Приближается решающий рубеж, который обычно преодолевается без особого труда.

3. Иррациональность. Когда пройдена критическая точка 10 евро, абсолютно всем становится понятно, что любой, кто продолжит делать ставки, окажется в проигрыше. Тот, кто сделал наивысшую ставку, заплатит за банкноту сумму, превышающую ее номинал, а предпоследний участник отдаст 10 евро просто так. Но теперь в участниках просыпается пещерный человек. Про стратегию, математику, расчеты и все трезвые мысли можно забыть. Люди отчаянно пытаются свести свой проигрыш к минимуму, думая: «Если сейчас я остановлюсь, то проиграю 10 евро, а если продолжу, то, возможно, обойдусь всего одним». Но эта тактика порочна. Единственно правильное решение – вообще не участвовать в таких играх.

Экономист Мартин Шубик, придумавший эту игру, часто разыгрывал на вечеринках в Нью-Йорке долларовую банкноту с начальной ставкой 1 цент. В среднем последняя ставка составляла 3,4 доллара, а поскольку деньги платил еще и предпоследний участник, за 1 доллар Шубик получал в среднем целых 7 долларов. Трудно поверить? Но это действительно так.

Ведь, кроме логики, здесь еще присутствуют жадность и «здравый смысл». А он чертовски нелогичен, как и биржевые тренды.

К таким играм можно отнести, например, войну во Вьетнаме (да, пожалуй, и любую другую войну). Игра Шубика появилась как раз в разгар американской военной катастрофы. Математики и экономисты моментально поняли, что «долларовый аукцион» представляет собой модель бессмысленной эскалации войны, в которой невозможно одержать победу, и демонстрирует иррациональное поведение вроде бы разумных, но одержимых неким желанием людей. Американский журналист Аллан Тигер написал по этому поводу книгу с разоблачительным названием «Останавливаться уже поздно». Вьетнамская война не сулила победы, поэтому она и продолжалась так долго, хотя профессиональные военные поняли это уже давным-давно.

Как могло случиться, что гигантский штаб, не испытывающий недостатка в профессионалах и высокообразованных людях, раз за разом принимал пагубные решения? Похоже, существует какой-то закон природы, который и лег в основу современной теории игр, разработанной Джоном фон Нейманом. Этот феномен иногда называют «западней „Конкорда“» (западней канала Рейн-Майн-Дунай или западней «Трансрапида»), так как расходы на разработку и производство совместного англо-французского сверхзвукового пассажирского самолета были настолько огромны, что любой экономист сразу понял бы: этот проект никогда не окупится. И действительно, «Конкорд» вплоть до самого конца приносил одни убытки. Можно было бы сэкономить намного больше, если бы сразу после завершения конструкторских работ этот проект был списан, а изготовленные опытные образцы переданы техническим музеям. Но этому не суждено было случиться, поскольку речь шла о престиже, а там, где экономика сталкивается с политическими амбициями, наступает катастрофа. Подтверждением этому могут служить войны, банкротства компаний и даже забастовки. Зачастую потери, причиненные забастовкой, настолько велики, что руководству фирмы дешевле было бы сразу согласиться на максимальные требования сотрудников. В свою очередь, участники забастовки теряют из-за отсутствия зарплаты намного больше, чем получат впоследствии, когда их требования будут удовлетворены. Что это? Сумасшествие? Нет, теория Неймана на практике.

Если вам все это кажется сложным, сделаем более простое предложение: выиграйте миллион! Нет, не в передаче «Кто хочет стать миллионером?» (для этого надо самому быть всезнайкой и вдобавок еще иметь такого же друга, которому можно позвонить). Мы не говорим ни о лотерее, ни о тотализаторе. Просто пришлите нам открытку и получите миллион евро. Но, как вы уже наверняка догадываетесь, здесь вновь вступает в игру правило Неймана. Приз достанется только одному человеку, но его размер зависит от количества претендентов. Если бы вы были единственным, кто пришлет открытку, то получили бы миллион. Но вероятность этого крайне низка. Скорее всего, таких наберется много, и миллион будет разделен на количество претендентов. Вскоре от него почти ничего не останется. Если бы редакция газеты Bild задумала разыграть миллион по таким правилам и в этой акции приняла участие всего половина ее читателей, на долю победителя досталось бы целых 30 евроцентов… Конечно, почта неплохо нажилась бы на этом, но кто-то же должен быть в выигрыше.

Какова же оптимальная тактика в подобных играх? В них надо учитывать новый и совершенно неожиданный фактор – мораль. Цель претендентов состоит в том, чтобы получить как можно больше (в идеальном случае – миллион). Цель устроителей акции – заплатить как можно меньше. И эта вторая цель выглядит куда реалистичнее, так как можно смело рассчитывать на людскую жадность. В данном случае жадность пагубна не только с моральной, но и с математической точки зрения. Самым лучшим было бы заранее разыграть среди претендентов право на участие в игре. Например, можно создать игральную кость с количеством граней, равным числу претендентов. Все они будут бросать ее по очереди, и тот, у кого выпадет единица, получит право послать открытку, а все остальные откажутся. Это, конечно, фантазия, поскольку желающих будет настолько много, что количество граней будет стремиться к бесконечности, но замысел вам понятен.

На практике же из теории игр Неймана можно сделать интересные выводы об оптимальном поведении в экономике. Здесь жадность вредна, а мораль приносит выгоду. И не потому, что конкуренты чтят моральные заповеди, а потому, что кооперация себя оправдывает, а конфронтация чаще всего вредит. Главная стратегия теории игр стара как мир, и ее уже не раз формулировали в самых разных выражениях, смысл которых сводится к одному: «Итак во всем, как хотите, чтобы с вами поступали люди, так поступайте и вы с ними» (От Матфея 7:12). Примерно о том же рассуждают Конфуций, Платон, Аристотель и Сенека. «Поступай так, чтобы максима твоего поступка посредством твоей воли должна была стать всеобщим законом природы», – гласит категорический императив Канта. Первоклассную стратегию выигрыша мы можем прочитать на стенах многих туалетов: «Покидая это место, оставьте его, пожалуйста, в том виде, в каком хотели бы его видеть при следующем посещении!»

Следует ли из этого, что добро всегда побеждает? Должен ли экономический выигрыш базироваться на морали? Пожалуй, это будет слишком смелым выводом из теории Неймана. Его необходимо проверить экспериментальным путем.

В 1950 году два математика, Меррил Флуд и Мелвин Дрешер, впервые предложили логическую дилемму, которая читается как детективный роман. Полиции удается поймать двух гангстеров (назовем их Антоном и Бруно). За ними давно идет охота, но в прошлом они постоянно ускользали от правосудия из-за недостатка улик. Их и в этот раз поймали только на мелком хулиганстве. Они сидят в разных камерах и не имеют возможности общаться. Прокурор делает одному из них предложение: «Если ты сознаешься в преступлениях, которые мы пока не можем доказать, то я тебя отпущу и даже закрою глаза на хулиганство, а твой сообщник получит пять лет тюрьмы. Но это только в том случае, если он не сознается. Если же он тоже напишет явку с повинной, в твоем признании будет мало толку и вы оба сядете на четыре года. Если ты будешь молчать, а твой подельник сознается, мы посадим на пять лет тебя. Но если вы оба будете запираться, то мы отправим обоих за решетку на два года за хулиганство. Твоему сообщнику я предложил то же самое. У вас обоих есть час, чтобы подумать. Решай сам. Через час ты в принципе можешь оказаться на свободе!»

Оба бандита не испытывают теплых чувств друг к другу и хотят отделаться наименьшим наказанием. Какое логическое решение будет для них правильным? Сознаваться или нет?

Таблица 1. Дилемма арестантов

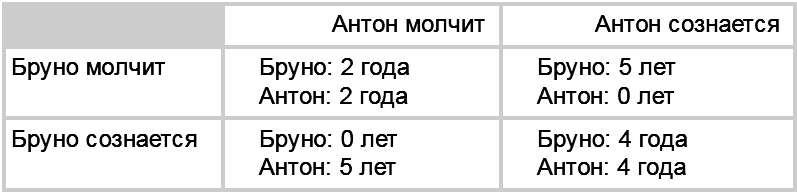
Поразмыслите над этой проблемой. Мы только хотим напомнить еще об одном моменте: если бы речь шла об известной гангстерской парочке Бонни и Клайде, их решение было бы простым и однозначным, а потому правильным. Но там в игру вмешивались чувства…

Вы полагаете, что подобные теоретические дилеммы не имеют отношения к реальной жизни? Не заблуждайтесь, это и есть реальность! Представьте себе, например, владельцев двух соседних автозаправочных станций. В начале каждого месяца им необходимо принимать решение, по какой цене продавать бензин в течение четырех последующих недель. Конечно, хорошо бы знать, что у конкурента на уме, но подобные вопросы удовлетворительно решаются только в рамках теории игр. Если один из них решит немного снизить цену в расчете на то, что ему удастся продать больше бензина и получить больше выручки, то второму нежелательно идти на поводу, так как в этом случае оба продадут меньше, да к тому же еще и по более низким ценам, чем в предыдущем месяце. Обоим лучше было бы равномерно и понемногу повышать цену и за счет этого увеличивать прибыль. Так почему бы им предварительно не договориться о более высокой цене? Потому, что подобные договоренности запрещены и называются преступным ценовым сговором. Для противодействия таким «оптимальным» решениям и создан специальный антимонопольный орган. Так что если у вас нет шпиона в стане конкурента, осваивайте теорию игр.

Совершенно очевидно, что теория игр имеет большое значение для проведения международных переговоров и конференций по разоружению. Но нужна ли она нам в повседневной жизни? Есть много ситуаций, в которых приходится принимать непростые решения: сделать предложение самому или ждать предложения от партнера? Идти ли на максимальный риск или избрать более осторожную тактику? Надо ли строго придерживаться ранее достигнутых договоренностей? Как предотвратить нарушение соглашений со стороны конкурентов? Как лучше всего провести переговоры? Какие действия необходимо предпринять? Все эти вопросы встают перед нами ежедневно, и зачастую мы принимаем решения без всякого логического анализа. Взять хотя бы так называемую проблему дележа без зависти. Она встречается и во внешней политике, и в семейных делах. Приведем классический пример: подчиненный идет пообедать в ресторан вместе с начальником. Тот предлагает взять общую порцию рыбы на двоих. Блюдо подается на стол, а на нем две рыбы: одна побольше, а вторая поменьше. Подчиненный берет себе большую рыбу, и начальник с недовольным видом говорит:

– Так не делается. Я взял бы себе рыбу поменьше.

– На что же вы жалуетесь? – отвечает подчиненный. – Ведь вам именно она и досталась.

Казалось бы, незатейливый анекдот, но за этой проблемой стоит высшая математика. Чтобы успешно что-то разделить, не вызывая зависти у соперника, необходимо делить, исходя не из своих интересов, а из его. Например, в ходе переговоров по разрешению пограничных споров представитель страны А должен прокладывать линию границы, руководствуясь не только своими интересами, но и требованиями страны Б. Умение поставить себя на место партнера приводит к компромиссам быстрее, чем классические переговоры с позиций соперничества. Кроме того, эти компромиссы эмоционально воспринимаются обеими сторонами как более приемлемые. В последнее время подобные сценарии все чаще используются в решении международных проблем и в ходе выработки тарифных соглашений.

Чтобы лучше понять принцип дележа без зависти, мы предлагаем вам решить следующую задачу. Два руководителя отделов претендуют на пост в правлении компании. Председатель правления сообщает, что, поскольку оба обладают одинаковой квалификацией, он хочет дать им особое поручение: «В ваших отделах равное количество сотрудников, имеющих одинаковую подготовку. Вы должны разработать план реформирования правления. Чей отдел представит худший план, тот и получит эту должность».

Оба начальника отделов некоторое время смотрят друг на друга с недоумением, но затем им приходит в голову, как в таких условиях организовать честное соревнование.

Принцип пирамиды известен с древних времен. Тем не менее по-прежнему находятся люди с криминальными наклонностями, успешно зарабатывающие деньги на использовании свойств этого простого экспоненциального математического ряда. Безобидной формой пирамиды в прошлом были письма, которые молодые люди отправляли своим сверстникам с просьбой посылать им открытки из мест проведения отпусков. Эта традиция родилась в те времена, когда люди еще коллекционировали почтовые марки, но теперь ее сменила массовая рассылка СМС и сообщений по электронной почте. Принцип, правда, остался прежним. Один человек становится инициатором пирамиды и шлет послание десяти другим (количество может меняться, но обычно составляет от восьми до двенадцати адресатов). Те переправляют его десяти другим людям из числа своих знакомых и так далее. Через пять циклов количество охваченных людей составляет уже 100 тысяч. На практике обычно не бывает так гладко, как в теории. Цепочка может оборваться (как правило, в самом начале), или адресаты по каким-либо причинам (страх подхватить компьютерный вирус или просто нежелание попусту тратить время) отказываются принимать участие в подобных играх. До тех пор пока в этой пирамиде не участвуют деньги, она не заслуживает особого внимания. Разумеется, кто-то все же немного зарабатывает на этом (телефонные сети, провайдеры мобильной связи), но настоящая денежная пирамида – это нечто совершенно иное. В самой простой форме она выглядит так: вы посылаете инициатору определенную сумму. За это он включает вас в свой список, который вы рассылаете другим людям в надежде получить от них во много раз больше денег. Но эта надежда оправдывается лишь в том случае, если вы входите в «первую волну» участников (то есть в число правонарушителей), которая скатывает снежный ком вниз по склону. Хотя в последнее время приходится встречаться с самыми разными красивыми названиями таких инициатив, речь идет лишь о новых наименованиях старой мошеннической схемы, к которой в немецком законодательстве сложилось совершенно однозначное отношение: игры, специально организованные таким образом, что лишь первые участники получают денежную прибыль, а основная масса теряет вложенные суммы, противоречат принципам ведения бизнеса и подлежат запрету (статья 138, часть 1 уголовного кодекса).

Пирамида развивается следующим образом: некто просит вас выслать тысячу евро на верхний уровень (одному из инициаторов). Получив, к примеру, 8 тысяч евро от восьми участников, он забирает всю сумму и выходит из игры, а вы и другие участники, выславшие ему деньги, поднимаетесь на его уровень и теперь должны сами находить новых участников, которые будут высылать деньги вам. Если вы вступили в уже действующую пирамиду, то можете только проиграть и к тому же обзаведетесь целой кучей недругов. Даже если каждый новый участник должен найти всего пять новых игроков, то после десятого цикла в игре должно чисто теоретически участвовать все население Германии. Как видите, незнание такого математического действия, как возведение в степень, может быстро привести к краху.

В 2004 году один немец и два австрийца, запустив в интернете такую пирамиду, пообещали участникам, что через четыре месяца вложенный капитал увеличится в восемь раз. В результате около 4 тысяч игроков потеряли в общей сложности более 8 миллионов евро. Минимальный взнос составлял 400 евро, а обещанный прирост – 1 процент в день. В день! Это 365 процентов годовых. Похоже, что жадность полностью лишила людей способности соображать. Некоторые особо жадные игроки вкладывали до 100 тысяч евро.

Почему наше логическое мышление отказывает с такой легкостью? Почему жадность затмевает разум? Возможно, к этому имеет отношение имеющийся в мозге «центр поощрений» – так называемое прилежащее ядро лимбической системы. Данная область мозга вызывает чувство удовольствия, когда мы добиваемся успеха. Однако она, как ни странно, активизируется и в том случае, когда кто-то из наших недругов терпит неудачу. Видимо, в этом злорадстве и кроется разгадка секрета. Если мы заведомо знаем, что каждый успех в такой пирамиде покупается ценой неудачи сотен других людей, то у нас не остается другой возможности, кроме веры в то, что мы и все прочие выигравшие относимся к числу «хороших», а все проигравшие – к числу «плохих». Разумеется, в них нет ничего «плохого», но они не принадлежат к нашему ближайшему окружению. В конце концов, это всего лишь знакомые знакомых знакомых. В том отделе мозга, который отвечает за этику и мораль, часто происходит смешение таких понятий, как знания и надежды, что мы уже видели, рассматривая дилемму арестантов. Именно поэтому мы предпочитаем забывать о своей вине.

Для пирамиды, основанной на эффекте снежного кома, характерны следующие признаки:

● Первое послание поступает к вам от человека, который имеет, по крайней мере, косвенное отношение к кругу ваших знакомых.

● Вас поздравляют с необычайно счастливой возможностью поучаствовать в этой игре.

● Чтобы в нее включиться, вы должны вложить какие-то средства, а также найти и завербовать новых участников.

Привлекая новых игроков, вы получаете вознаграждение, но главная цель – это большой выигрыш. В разных пирамидах условия его получения могут иметь отличия.

В некоторых пирамидах производится распространение каких-то товаров – чаще всего абсолютно бесполезных и по завышенным ценам. Их продажа служит своего рода алиби. С ее помощью попросту маскируется вознаграждение за привлечение новых членов.

Особую роль играют так называемые семинары участников, на которых царит атмосфера усиленной манипуляции сознанием. Людей, которые скептически реагируют на «правила игры» и задают критические вопросы, как правило, быстро изгоняют. При этом в их адрес звучат высказывания типа «Если вы не хотите стать миллионером – скатертью дорога». Давление со стороны целой группы выдерживают далеко не все.

Неизбежный крах любой пирамиды можно доказать чисто математически. В выигрыше оказываются лишь инициаторы. Доля проигравших составляет минимум 87,5 процента. Но к финансовым потерям надо добавить еще эмоциональные и социальные. Ведь вы, как правило, вовлекаете в эту деятельность своих друзей и родных. Когда они тоже оказываются в проигрыше, это влечет за собой утрату доверия к вам.