Классические античные представления о мышлении

Уже 3 тысячи лет назад (в этом мы полностью уверены) люди упражнялись в развитии своего логического аппарата и обучали учеников, разгадывая загадки и решая задачи в игровой форме. Загадкой называется интеллектуальное задание, которое можно выполнить только за счет работы мысли. В античные времена было широко распространено мнение, что подобные игровые действия тренируют мозг точно так же, как спорт укрепляет мышцы. Старейшим документом такого рода является задача Ахмеса, написанная на папирусе, который датируется примерно 1650 годом до нашей эры:

«Есть семь домов. В каждом доме живет по семь кошек. Каждая кошка съела по семь мышей, каждая из которых, в свою очередь, съела семь колосьев, в которых было по семь семян. Сколько всего предметов – начиная от зерна и заканчивая домом – описывается в этой истории?»

Если вы уже знакомы с этой задачей, то вряд ли удивляетесь тому, что египтяне были помешаны на пирамидах. Эта геометрическая фигура, как никакая другая, символизирует действие возведения в степень и придает ему не только математическое, но также иерархическое и Божественное значение. Можно только представить себе, с каким изумлением первые математики с берегов Нила наблюдали стремительное увеличение чисел в геометрической прогрессии.

Однако подобные числовые чудеса были знакомы также арабским, индийским и центрально-американским математикам. Мы можем привести вам одну из самых красивых классических задач, хотя она является лишь легендой. Говорят, что примерно за 300 лет до Рождества Христова некто Сисса ибн Дахир из Индии изобрел шахматы. Когда он продемонстрировал новую игру радже, тот был настолько восхищен, что предложил создателю исполнить любое его пожелание. В качестве награды скромный Сисса ибн Дахир попросил дать ему столько рисовых зерен, сколько окажется на шахматной доске, если на первую клетку положить одно зерно, на вторую – два зерна, на третью – четыре и так далее, последовательно удваивая количество зерен вплоть до 64-й клетки. Согласно легенде, раджа посмеялся над глупым Сиссой, но тот, помимо изобретения шахмат, успел до этого открыть для себя чудо экспоненциальной функции: 1 + 2 + 4 + 8 + … = 2⁰ + + 2¹ + 2² + 2³ + … + 2⁶³. Произведя подсчеты, мы обнаружим, что на 64-й клетке доски окажется девять квинтиллионов двести двадцать три квадриллиона триста семьдесят два триллиона тридцать шесть миллиардов восемьсот пятьдесят четыре миллиона семьсот семьдесят пять тысяч восемьсот восемь зерен (или в числовом выражении 9 223 372 036 854 775 808).

Существует немало изящных способов выразить всю масштабность данного числа. Например, если погрузить весь этот рис в грузовики, то получится колонна, которая 200 тысяч раз обогнет весь земной шар. Всего годового урожая риса в мире не хватило бы, чтобы расплатиться с хитрым Сиссой ибн Дахиром. Для этого понадобилось бы выращивать рис в течение тысячи лет. И все же раджа придумал ответный ход. Он обещал расплатиться с изобретателем в соответствии с его пожеланием, но с условием, что тот будет сам считать зерна. Гениальный шахматный ход.

Как уже сказано, это всего лишь легенда. Но лучше хорошая легенда, подсказывающая нам логические взаимосвязи, чем сухая формула, которая быстро забывается.

О всевозможных загадках и логических задачах рассказывается и в Ветхом Завете (их загадывала Соломону царица Савская), и в индогерманской мифологии, и в античных памятниках письменности. Примером последнего может служить легенда об Эдипе и содержащаяся в ней загадка Сфинкса, согласно которой городу Фивы угрожал ужасный Сфинкс (демон разрушения, изображавшийся в виде крылатого льва с головой женщины и хвостом змеи). Он загадывал каждому проходящему загадку. Если человек не мог ее разгадать, Сфинкс убивал несчастного. Только Эдип смог первым найти правильный ответ. Загадка звучала так:

«Кто ходит утром на четырех ногах,

днем на двух, а вечером на трех?

Ни у одного из других существ, живущих на земле,

количество ног не меняется.

Чем больше у него ног, тем меньше сил

и тем медленнее он передвигается».

Когда Эдип дал правильный ответ, Сфинкс умер от стыда.

Сегодня разгадывание загадок не связано с таким драматизмом. В наши дни они предназначены больше для детей. Многие математические правила и принципы в литературной обработке находят место в сборниках логических задач наряду с кроссвордами и судоку. Но дело не в том, в какой форме выступают эти вербальные возбудители нейронов. Они по-прежнему чрезвычайно эффективны и побуждают нас к творческому, разностороннему и целенаправленному мышлению.

Давайте пройдемся вместе с вами по истории загадок. Древние греки были буквально помешаны на переводе математических, логических и физических знаний в форму различных историй и загадок. Известен классический парадокс о том, как Ахилл и черепаха бегали наперегонки и наш быстроногий герой одержал победу. Но черепаха попросила еще об одной попытке, в которой у нее будет небольшая фора. Ахилл согласился, и в этом была его ошибка. Древнегреческий философ Зенон построил на этом свой тезис, в соответствии с которым Ахилл никогда не догонит черепаху. Пока он добежит до той точки, с которой стартовала черепаха, она немного продвинется вперед, и у нее снова возникнет фора, пусть даже и меньше той, которая была первоначально. Когда Ахилл сократит и это отставание, она снова немного уйдет вперед, и так далее. Мы, конечно, понимаем, что это ложное заключение, но данный парадокс до сих пор дает нам пищу для размышления. Как же доказать, что Ахилл все-таки перегонит черепаху?

Бег наперегонки – это вообще излюбленная тема логических задач. Вот еще один вопрос, который не является парадоксом, а имеет логически обоснованное решение. Ахилл и его друг Патрокл решили устроить соревнования по бегу на 100 метров (хотя в античные времена такая мера длины не использовалась). Когда Ахилл пересекает финишную черту, Патрокл находится в 5 метрах позади него. Ахилл дает своему другу право на реванш, но на этот раз решает уравнять шансы. Он стартует в 5 метрах позади Патрокла. Кто победит на этот раз?

Загадка или ритуал посвящения: легенды и сказки

Магические загадки из мифов превратились в народные загадки, которые, подобно народным песням и стихам, передавались из уст в уста. Они стали частью рассказов и сказок, которые дошли до наших дней из Китая, Индии, Персии, арабского и европейского мира. С появлением письменности загадки начали записывать наряду с религиозными текстами, но зачастую они носили характер ритуалов посвящения или облекались в форму мудрых заповедей. Из письменных источников VII века до нас дошли вопросы, с помощью которых выяснялось, насколько хорошо читатели знают Библию. Например: «Qui est mortus et non est natus?», что в переводе с латыни означает: «Кто умер, не будучи рожденным?» А как у вас обстоят дела со знанием Библии?

При изучении каталогов европейских рукописных источников VIII–XIX веков было обнаружено около 7750 текстов, содержащих загадки. После изобретения книгопечатания начала издаваться общеполезная литература, в том числе и всевозможные головоломки. В 1505 году появилась первая подобная книга на немецком языке – «Страсбургская книга загадок». Загадки содержались также в легендах и сказках, которые передавались из поколения в поколение на протяжении многих веков. Среди прочих к этому приложили руку братья Якоб и Вильгельм Гримм. В сказке об умной крестьянской дочери показано превосходство девушки, умеющей разгадывать загадки, над могущественным, но недалеким королем.

Умная дочь крестьянская

Жил когда-то на свете бедный крестьянин; земли у него вовсе не было, и была у него всего лишь одна небольшая избушка да единственная дочка. Вот и говорит раз дочка отцу:

– Надо бы нам выпросить у короля хоть какой-нибудь кусок пустоши.

Услыхал король про их бедность и подарил им клочок луга. Перепахала она его вместе с отцом, и собрались они посеять на нем рожь да еще что-нибудь. Вспахали они уже почти все поле и вдруг нашли в земле ступку, а была она из чистого золота.

– Знаешь что, – сказал отец дочке, – господин король был так милостив, что подарил нам эту землю. Давай отдадим мы ему за это золотую ступку.

Но дочь на это не согласилась и говорит:

– Батюшка, если есть у нас одна только ступка, а пестика нету, то с нас ведь потребуют еще и пестик. Лучше уж вы помолчите.

Но отец ее не послушался, взял ступку, отнес ее королю и сказал, что нашел ее на лугу, и спросил, не примет ли он ее от него в дар. Взял король ступку и спрашивает:

– А не находил ли ты еще чего?

– Нет, – ответил крестьянин.

И сказал король, чтоб доставил он ему и пестик. Крестьянин сказал, что такого они, мол, не находили, но этот ответ помог ему мало – все равно что говорить на ветер. И посадили его в темницу, чтобы сидел он там, пока не достанет пестик. Тюремщики приносили ему каждый день хлеб да воду – то, что в тюрьме полагается; и услыхали тюремщики, как он все повторял про себя: «Ах, если б я послушался своей дочери!», «Ах, если б я послушался своей дочери!» Тогда пошли тюремщики к королю и доложили, что узник все кричит и повторяет: «Ах, если б я послушался своей дочери!» – а от пищи и питья отказывается. Тогда король приказал тюремщикам привести к нему узника и спросил его, отчего это он все кричит: «Ах, если б я послушался своей дочери!»

– Что же такое сказала твоя дочь?

– Да она сказала, чтоб я не относил вам ступки, а то потребуют с меня еще и пестик.

– Если у тебя такая разумная дочь, то пускай она явится ко мне.

И вот пришлось ей идти к королю, и стал он спрашивать, так ли она уж умна и вправду; и сказал, что хочет задать ей одну задачу; если она ее решит, то он женится на ней. Она тотчас сказала «хорошо» и согласилась ее решить. Тогда король и говорит:

– Приходи ко мне не одетая и не голая, не верхом и не в повозке, не путем, а все же дорогою. Если ты сможешь это выполнить, то я на тебе женюсь.

Вот пошла она, разделась совсем догола – и стала она неодетая; взяла большую рыбачью сеть, стала в нее и укуталась ею – вот и не была она голая; наняла она себе за деньги осла и привязала ту сеть к ослиному хвосту, чтоб тащил он ее, – вот и не ехала она ни верхом, ни в повозке; а осел должен был тащить ее по колее, и касалась она земли одним только большим пальцем ноги – и вот шла она ни путем, ни без дороги. Вот явилась она, и король сказал, что задачу она решила и все выполнила как следует. Велел он тогда выпустить ее отца из темницы, взял ее себе в жены и отдал в ее распоряжение всю королевскую казну.

И вот вам для разнообразия эпизод еще из одной народной сказки. Злая колдунья превратила трех женщин в алые розы. Одна из роз получила разрешение навестить своего мужа в женском обличье и провести с ним целую ночь, а на рассвете вернуться обратно. «Если ты завтра утром придешь на волшебный луг и сорвешь меня, – сказала она мужу, – то избавишь меня от злых чар. Но сорвать ты должен только меня, а не другой цветок, иначе все мы пропадем навек. Тебе нельзя следить за мной, когда я буду уходить, поэтому придумай сам, как ты отличишь меня от других цветов». По какому же признаку муж узнал свою жену в облике розы?

Однако большинство загадок в период между античными временами и эпохой Просвещения были, скорее, богословскими или моральными заповедями, которые указывали на величайшую и неразрешимую загадку – на Бога. Во все времена встречались люди, которые были ближе к Богу, чем другие. Коран пишет о Мухаммеде, Ветхий Завет – о Моисее, Новый Завет – об апостоле Петре, но самая главная тайна оставалась скрытой и для них. Существуют неразгадываемые загадки. В самой их формулировке содержится указание на Сущность, которая одна знает ответы на все вопросы. Сегодня мы сказали бы, что они носят философский характер, но в те времена за ними стояло богословие. Неразрешимая загадка – это тайна, которую невозможно понять, даже если все называли «учеными» людей, которые занимались этой темой.

Что выше Бога

и порочнее дьявола?

Им обладают бедняки,

в нем нуждаются счастливые,

а если ты будешь им питаться, то умрешь!

Головоломки в литературе

Классики – от Гомера до Сервантеса и Гриммельсгаузена, Шиллера и Гёте – использовали в своих романах загадки и логические задачи. Чаще всего они должны были доказать мудрость главных героев. Так, например, в романе Сервантеса «Дон Кихот» верный оруженосец Санчо Панса должен дать ответ на вопрос, который подтвердит его пригодность к должности губернатора острова. К нему подходят два старика и просят по справедливости разрешить их тяжбу. Один из них дал взаймы другому десять золотых. Прождав долгое время, он обратился к должнику за деньгами, но тот ответил, что уже вернул их. Кредитор же настаивал на том, что никаких денег не получал. Свидетелей займа и отдачи не было. Тогда Санчо Панса спросил, поверит ли кредитор должнику, что деньги уже возвращены, если тот поклянется в этом на Библии. Кредитор выразил свое согласие с таким решением. Перед тем как возложить руку на Библию, должник попросил своего соперника в этом споре подержать его посох и поклялся, что отдал деньги. После этого он забрал свой посох и собирался уже уйти, но Санчо Панса, выглядевший простаком, доказал свою крестьянскую сметку. Он сделал совершенно однозначный вывод о том, что человек, приносящий клятву на Библии, солгать не может (во всяком случае, в Испании XVI века!), но ему показалось странным, что на время клятвы он отдал свой посох в руки жалобщика. Следовательно, деньги находились в посохе. Так оно и оказалось. Красивая история и прекрасный пример логических умозаключений.

Вся история культуры и литературы полна не только загадок, но и весьма загадочных персонажей. Как вы думаете, что могло бы произойти, если бы они вдруг встретились? Правильно, между ними началась бы загадочная беседа. Персонаж многих немецких басен Бальдандерс изложил ее в форме загадки:

Из этой беседы ты узнаешь, кто владеет абсолютной истиной. Нострадамус заявил: «Обладателями абсолютной истины являются либо Гермес Трисмегист, либо скоморох Леффельштиль». Ему возразил святой Франциск: «Нет, Гермес Трисмегист этой истины не знает». Гермест Трисмегист в свою очередь сказал: «Ее знает Б. Травен». Но Б. Травен опроверг это: «Нет, я ее не знаю». Под конец Леффельштиль сказал: «Двое из нас сказали неправду». Из этого ты сможешь сделать вывод, кто владеет абсолютной истиной.

Вам предстоит разобраться, кто же на самом деле обладатель абсолютной истины. Не сдавайтесь слишком быстро. Ведь не может же быть, чтобы вас заткнул за пояс какой-то персонаж басен! Если два человека солгали, следовательно, остальные сказали правду. Это поможет вам в поисках. Подумайте, чьи высказывания были правдивы, и не позволяйте сбить себя с толку.

В персидском сборнике рассказов «Тысяча и один день» (не путать с известными сказками «Тысяча и одна ночь») мы знакомимся с жестокой принцессой Турандот, которая загадывает своим женихам загадки и лишает их головы, если они не находят ответа. В конце концов появляется некий принц, которому удается разгадать все три загадки: «Что рождается каждую ночь и умирает на рассвете?» (Надежда.) «Что пылает подобно пламени, но не пламя?» (Кровь.) «Что похоже на лед, но обжигает?» (Турандот.) Казалось бы, можно играть свадьбу, но принц понимает, что так он никогда не завоюет ее любовь. Поэтому в свою очередь предлагает принцессе загадку: она должна угадать его имя. Если ей это удастся, она может распорядиться его жизнью, как ей будет угодно. Поскольку принц находится вдали от родины, он уверен, что никто его здесь не знает, но одна из рабынь Турандот (когда-то похищенная принцесса, которая любила принца) узнает его и предлагает бежать вместе с ней. Принц отвергает ее предложение, и она, пылая чувством мести, выдает Турандот его имя. Но все кончается благополучно: Турандот признается принцу в любви, и они вместе восходят на трон. Мы так подробно пишем обо всем этом, чтобы продемонстрировать, какое место занимают загадки, пророчества и хитрые логические задачи в истории литературы. Загадки всегда были не просто упражнением для мозга, а некими моральными вехами, Божественными откровениями, выражением древней мудрости.

В завершение нашего литературного экскурса предлагаем вам загадку от нашего старого доброго знакомого тайного советника Гёте:

Он брат среди многих братьев и ничем не отличается от них. Он столь же дорог и ценен, как и все остальные, но появляется в семье лишь изредка и к нему относятся, словно к приемному ребенку.

Загадки как урок естествознания

В большинстве логических задач находят отражение наши познания в математике и физике. Такие задачи позволяют не только детям, но и взрослым людям понять, какое значение имеет математика в повседневной жизни, даже если все выученные в школе формулы давно забыты. В качестве примера приведем классическую историю. На берегу реки стоит крестьянин с волком, козой и капустой. Он хочет перевезти их на другой берег, но его лодка настолько мала, что он может взять с собой только что-то одно: либо волка, либо козу, либо капусту. И вот тут возникает проблема: если оставить вдвоем волка и козу, волк съест козу. Если оставить козу и капусту, коза съест капусту. Как же переправить всех троих? Такие взаимоисключающие комбинации постоянно встречаются в прикладной математике. Это хорошо известно кибернетикам и программистам.

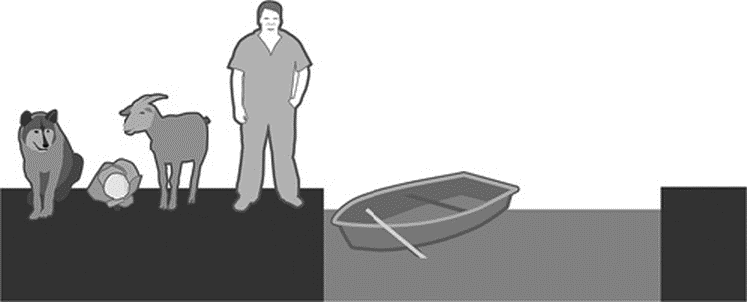
Рис. 8. Капуста, коза, волк и крестьянин создают при разбивке по парам опасные сочетания

Еще одна классическая задача математика Жозефа Бертрана, составленная в 1888 году, посвящена теории вероятности. У нас есть три комода, и в каждом из них по два ящика. В первом комоде в обоих ящиках лежит по золотой монете, во втором комоде в каждом ящике лежит по серебряной монете, а в третьем комоде в одном ящике лежит золотая, а во втором – серебряная монета. Нам надо наугад открыть любой ящик в одном из комодов. Какова вероятность того, что там лежит золотая или серебряная монета? Совершенно очевидно, что она составляет один к трем. Итак, мы открываем ящик и находим там золотую монету. Какова теперь вероятность, что во втором ящике того же комода лежит серебряная монета? Вероятно, ваш ответ будет 50:50, но мы предлагаем вам спокойно подумать еще раз.

В 1920-е годы в Америке была очень популярна одна задача. Она настолько завоевала умы, что вместо приветствия люди зачастую спрашивали друг друга: «Так сколько же лет Анне?» Условие задачи звучит так: «Мэри 24 года. Сейчас ей вдвое больше лет, чем было Анне, когда Мэри было столько же лет, сколько Анне сейчас. Сколько сейчас лет Анне?»

Но и в наши дни хитроумные математические задачи (с которыми порой не справляются даже профессионалы) занимают умы людей. Это доказала задача с тремя дверями, предложенная на телешоу «Давайте заключим сделку». Десятки американских профессоров математики дружно высмеяли писательницу Мэрилин вос Савант, которая заявила, что участвующий в шоу кандидат может существенно повысить свои шансы на выигрыш, если поменяет свое же первоначальное решение. Представьте себе, что вы участвуете в этом шоу и стоите перед тремя дверями. За двумя из них ничего нет, а за третьей находится главный приз. Ведущий просит вас выбрать одну дверь, но пока не открывать ее. Совершенно очевидно, что вероятность успеха составляет один к трем. После этого ведущий (который, естественно, знает, где находится приз) открывает одну из двух оставшихся дверей и показывает, что там ничего нет. А теперь он предоставляет вам право выбора. Вы можете остаться при своем прежнем решении или открыть другую оставшуюся дверь. На первый взгляд кажется, что никакой разницы нет. Здравый смысл подсказывает, что вероятность в любом случае будет 50:50. Какой же смысл менять свое решение? Именно такой вывод был сделан большинством математиков.

Но они ошибались. Мэрилин вос Савант (чей IQ, кстати, составляет 228) путем расчетов убедила специалистов, что если кандидат останется при прежнем решении, то его шансы по-прежнему будут составлять 1:3, а вот если он выберет другую дверь, то они возрастут до 2:3. Это значит, что, поменяв решение, кандидат может выиграть (чисто статистически, разумеется) в двух случаях из трех.

К повседневным проблемам следует подходить точно так же, как к логическим задачам. Допустим, лучший сотрудник отдела одновременно обладает несносным характером, и с ним никто не хочет работать; браузер постоянно зависает на одном и том же сайте; банк согласен выдать вам кредит для открытия собственного бизнеса только после того, как вы откроете этот бизнес… Ведь все это, собственно говоря, и есть логические задачи, решение которых лишь в редких случаях лежит на поверхности. Следовательно, к решению этих производственных и личных проблем следует применять те же принципы, что и к головоломкам.

Стратегия решений

1. Изучение проблемы. Тщательно проанализируйте все детали и их взаимосвязи.

2. Созревание. Если проблема не решается быстро (и полностью), запомните информацию и носите ее в голове. Не думайте о ней постоянно, позвольте работать подсознанию.

3. Озарение. В какой-то момент вы почувствуете, что проскочила искра. Перед вами откроются новые взаимосвязи, и направление решения станет очевидным.

4. Проверка. Теперь вы можете сознательно работать над проблемой. Если решение найдено, не доверяйте ему слишком быстро. Тщательно перепроверьте его со всех точек зрения.

Но, как и в жизни, логические задачи подразделяются на несколько типов, и их необходимо распознавать. Бывают задачи простые, из области комбинаторики, бывают такие, в которых скрыт парадокс, а бывает всего лишь игра слов и смыслов, какой-то математический фокус или элементарный подвох.

Последние встречаются очень часто. Вот вам простой пример: самолет разбивается точно на границе Франции и Германии. Где будут хоронить выживших? Ага, сумели заметить подвох! Очевидно, мы недооценили ваш IQ. Ну, тогда для вас не составит большого труда решить и следующую задачку. Отец и сын возвращаются с горного курорта. На заснеженной автостраде автомобиль заносит, и он врезается в грузовик. Отец погибает на месте, а сына с тяжелейшими травмами головы доставляют на вертолете в ближайшую клинику. Ему срочно требуется операция на мозге, поэтому уже через час из столицы прилетает светило нейрохирургии. Однако при обследовании хирург внезапно заявляет: «Я не могу его оперировать. Это мой сын!»

Чтобы быть готовым к подобным подвохам в повседневной жизни, надо усвоить основные правила решения логических задач:

● Тщательно изучите вопрос. Рассмотрите его со всех сторон и убедитесь, что речь идет не о риторическом вопросе, который не требует ответа.

● Подходите к делу с уверенностью в себе. Если вопрос задан всерьез, на него можно найти ответ. Пусть не сразу, может быть, даже не в этом месяце, но для вас нет ничего невозможного. Если вы не разбираетесь в какой-то области, обратитесь к специалисту.

● Проанализируйте все взаимосвязи. Какие-то проблемы можно обобщать, но ваша особенная. Не думайте, что она сформулирована именно так по чистой случайности!

● Не уходите с головой в решение. Логические задачи далеко не всегда решаются целенаправленно. Дайте волю интуиции и фантазии. Правильный путь – это чаще всего свободный полет мысли, выходящий за привычные рамки.

● Не устанавливайте для себя ограничений. Зачастую задача кажется сложной лишь потому, что вы сами придумали себе слишком узкие рамки решения, которых в действительности не существует.

● Реальные проблемы и логические задачи зачастую похожи друг на друга. Если понятен их принцип, они решаются мгновенно. Если в логической задаче вы имеете дело, к примеру, с двумя племенами индейцев, одно из которых постоянно лжет, а другое всегда говорит правду, то в реальности вы можете столкнуться с начальниками, которые ведут себя подобным образом. Предупрежден – значит вооружен!

● Переверните проблему с ног на голову! Попробуйте вместо поиска возможного решения выяснить, каким это решение не может быть в принципе! Зачастую подход с противоположной стороны быстрее ведет к решению.

Классические задачи для разминки

Улитка упала в колодец. Хорошо еще, что в нем не было воды, иначе она утонула бы. Но теперь перед ней стоит задача подняться наверх. Высота колодца 18 метров. При всем старании улитка может подняться за день только на 7 метров, а ночью опять сползает на 4 метра. На какой день она выберется из колодца?

В пруду растет одна кувшинка. Разрастаясь, она за день удваивает покрываемую площадь пруда. Через 30 дней весь пруд полностью покрыт кувшинками. Сколько дней понадобится, чтобы полностью покрыть весь пруд, если бы вначале была не одна кувшинка, а четыре?

Даже цветы могут символизировать числа. На лугу растет 35 цветов: красных, розовых и белых, – причем розовых в два раза больше, чем белых. Если сорвать четыре цветка, то по крайней мере один из них обязательно будет красным. Сколько цветов каждого цвета растет на лугу?

Два маляра красят дом. Оба работают с одинаковой скоростью. Вдвоем они покрасили бы этот дом за три дня, но после первого дня работы один из маляров заболел, и его коллега вынужден заканчивать работу в одиночку. Через сколько дней дом будет полностью покрашен?

У нас есть две литровые бутылки, одна из которых наполовину наполнена вином, а вторая – наполовину водой. Мы переливаем стакан вина (четверть литра) в бутылку с водой, хорошо перемешиваем и вновь переливаем стакан полученной смеси (также четверть литра) в бутылку с вином. В какой бутылке содержание вина будет больше?

Все это классические математические задачи, но умело обработанные и преподнесенные в занимательной форме, в отличие от тех примеров, которые вам приходилось решать в школе. Разница в том, что здесь, конечно, можно применять математические формулы (если вы вспомните подходящие), но больше требуются логика и воображение. Яркий пример отличия логики от математики демонстрирует следующая задача.

Два пешехода, расстояние между которыми составляет 12 километров, одновременно начинают двигаться навстречу друг другу со скоростью 4 километра в час. В момент начала движения птица, сидящая на плече первого пешехода, взлетает и мчится ко второму. Поравнявшись с ним, она разворачивается и снова летит к первому. Так продолжается до тех пор, пока пешеходы не встретятся. Скорость птицы – 30 километров в час. Сколько километров в общей сложности она пролетит до момента встречи?

Эта задача решается, как правило, с помощью геометрических рядов. Опытные математики находят ответ, не задумываясь, но им и в голову не приходит, что это можно сделать по-другому и намного проще. А вы додумались?

Элегантные упрощения свидетельствуют о творческом складе ума. Разумеется, это не значит, что все математики (включая учителей) полностью лишены этого качества. Один из самых известных математиков Карл Фридрих Гаусс, родившийся в Брауншвейге в 1777 году, на собственном опыте познал, что творческое мышление одновременно несет и радость, и муки. Когда ему было десять лет, учитель математики дал классу задание сложить все числа от 1 до 100. Маленький Гаусс справился за одну минуту, и ответ оказался верным. Но учителя это не обрадовало, так как он заподозрил ученика в обмане. Разве он мог подумать, что этот малолетний гений по ходу дела самостоятельно дошел до открытия бинома Ньютона. Он просто внимательно изучил задачу и заметил, что каждая последовательная пара чисел, взятых с начала и конца этого ряда, всегда дает в сумме 101 (1 + 100, 2 + 99, 3 + 98, 4 + 97 …) и таких пар насчитывается 50. В результате он просто умножил 50 на 101 и получил ответ: 5050.

Это поразительно красивое решение. А ведь красота, эстетика и ясность почти всегда являются признаками успешного решения задачи. Если доказательство изящно, оно должно быть верным. Точно так же химик, видя перед собой эстетичную модель молекулы, сразу приходит к выводу, что она «правильная». То же самое можно сказать и о физике, рассматривающем простую и изящную формулу. Если мысль красива, то и полученные в результате доказательства будут простыми и ясными, пути решения – элегантными, а выводы – убедительными. Даже если вы знаете, как обычно решается тот или иной тип задач или проблем, попробуйте сделать это иначе. Отвлекитесь от формул и диаграмм, доверьтесь интуиции, сознательно сделайте абсурдное допущение. Зачастую это ведет к решению. Вы уже знаете, что мозг – очень гибкий самоорганизующийся орган. Старайтесь руководствоваться этим в своих размышлениях. Большинство открытий и изобретений появились именно таким образом.

Эврика! Прикладные логические задачи

Найдя решение заковыристой задачи, можете смело кричать «Эврика!». Согласно легенде, именно так воскликнул Архимед, найдя в своей ванне ответ на мучивший его вопрос. Сиракузский царь Гиерон очень ценил самого знаменитого математика античности, поэтому поручил ему крайне щекотливое задание – узнать, из чистого ли золота сделана его новая царская корона. Архимед, естественно, не имел возможности расплавить корону. Кроме того, в то время еще не существовало химических методов анализа для определения содержания золота в сплаве. Задача оказалась трудной. Тут было над чем поломать голову. А теперь давайте прочертим линию между двумя, казалось бы, не связанными между собой вопросами, которая привела к искомому результату. Первый вопрос был уже поставлен: «Сделана ли корона из чистого золота?» Второй вопрос пришел Архимеду в голову, когда он улегся в наполненную доверху ванну и вода перелилась при этом через края. «Почему вылилось именно столько воды?» – заинтересовался он. Ответ на второй вопрос был ему понятен: тело, помещенное в жидкую или газообразную среду, вытесняет часть вещества, соответствующую его объему. Но это был одновременно и ответ на задачу, поставленную Гиероном. Архимед погрузил корону в наполненный до краев сосуд и посмотрел, сколько воды она вытеснила. Затем он поместил туда же золотой слиток, равный по весу короне. Корона вытеснила больше воды, чем слиток. Значит, она была сделана из более легкого металла. Следствием этого события стал знаменитый закон Архимеда, который определяет величину выталкивающей силы. Поскольку плотность золота выше, чем плотность воды, оно тонет и при этом вытесняет жидкость в количестве, равном его собственному объему. Более дешевый металл, правда, тоже тонет, но его плотность меньше, чем у золота, поэтому он вытесняет больший объем воды. Если же плотность предмета меньше, чем плотность воды, он плавает по поверхности.

Рис. 9. Архимед открывает выталкивающую силу. Гравюра на дереве из труда Витрувия «Десять книг об архитектуре», Венеция, 1511 год

Архимеду не были знакомы ледяные кубики для охлаждения вина, поэтому попробуйте дать за него ответ на следующий вопрос: в кружке, наполненной до краев водой, плавает кубик льда. Что будет, когда он растает?

Все мы постоянно проделываем эксперименты, но чаще всего даже не осознаем этого. Мы наблюдаем за окружающим миром, а когда он ставит перед нами очередную проблему, подсознательно начинаем обращать больше внимания на те наблюдения, которые так или иначе с ней связаны. Вот вам еще одна проблема. В банковском сейфе имеется 30 ячеек, в каждой из которых хранится по 30 золотых монет. Поступила информация, что в одной из ячеек монеты фальшивые. Настоящая золотая монета весит 10 граммов, а фальшивая – только 9 граммов. Директору банка необходимо узнать, в какой именно ячейке находятся фальшивые деньги, но у него очень мало времени, так как ревизия уже на пороге. У него есть электронные весы, позволяющие взвешивать с точностью до 1 грамма, но времени хватает только на одно взвешивание. Каким же образом можно определить, в какой ячейке фальшивые монеты?

Процедуры взвешивания и измерения постоянно встречаются в задачах, потому что чисто математические действия в этом случае легче трансформировать в форму занимательной истории. Итак, еще одна классическая задача. Перед вами лежат двенадцать металлических шариков, которые на вид не отличаются друг от друга, но один из шариков тяжелее остальных. У вас есть обычные рычажные весы, и вы можете произвести только три взвешивания. Как найти более тяжелый шарик? Ладно, с этой задачей вы, вероятно, справились быстро. А теперь немного усложним условие. Перед вами все те же двенадцать шариков, но один из них либо легче, либо тяжелее других. У вас по-прежнему только три попытки.

Хуже, когда на весы нельзя полностью положиться. Допустим, вы хотите отмерить 2 килограмма сахара. У вас есть рычажные весы, но с разной длиной плеч, килограммовая гиря, несколько бумажных пакетов и большой мешок сахара. Как вы поступите?

Одна упаковка чая весит 75 граммов, но покупателю нужно только 55 граммов. У продавщицы есть рычажные весы, но нет необходимых мелких гирек. Единственное, чем она располагает, – это пакетик шафрана, весящий 25 граммов, и пакетик с сахаром весом 40 граммов. Есть ли у нее возможность взвесить 55 граммов чая?

Крестьяне в Тироле до сих взвешивают яблоки с помощью четырех камней различного веса и рычажных весов. Если разбить 40-килограммовый мельничный жернов на четыре части, с их помощью можно взвешивать любой предмет весом от 1 до 40 килограммов. Вопрос лишь в том, какого веса должны быть эти части жернова.

Раз уж вы так увлеклись взвешиванием, предложим вам последнюю задачу с рычажными весами. На обеих чашах весов стоят наполненные одинаковым количеством воды банки. В одну банку поставим розу. Вторую розу такого же веса положим поверх второй банки, чтобы она не касалась воды. Весы пока находятся в равновесии. Что с ними произойдет, когда вторая роза засохнет?

Вообще-то весы – символ уравнения. Все, что находится на их чашах, можно представить в виде чисел. Но символизировать различные числа могут также песочные часы или ведра с водой. Вот несколько примеров.

У вас есть двое песочных часов. В одних песок полностью пересыпается из верхней емкости в нижнюю за 7 минут, а в других – за 4 минуты. Можно ли с их помощью отмерить ровно девять минут?

У вас есть два ведра. Одно вмещает ровно 3 литра воды, а второе – 5 литров. Никаких отметок на них не имеется. Вы стоите у колонки с водой, и вам нужно отмерить ровно 4 литра. Как это сделать?

Необходимо заполнить водой цистерну. У вас есть четыре насоса различной мощности. Самый мощный может заполнить цистерну за 1 час, второй – за 2 часа, третий – за 3 часа, а четвертому для этого понадобится 6 часов. Поскольку работа срочная, вы одновременно включаете все насосы. Через какое время цистерна будет заполнена?

Возможно, нашей часто критикуемой школьной системе пошло бы на пользу, если бы она подключила к изучению математических формул логику и воображение учащихся. Подумайте сами, какая формула поможет нам решить следующую задачу: осенняя буря повредила флагшток высотой 9 метров. Он сломался в 4 метрах от земли. На каком расстоянии от основания касается земли кончик сломанного флагштока?

С помощью подобных задач можно залезть в дебри математики. Например, если в помещении было три гнома, но четверо из них вышли, то должен зайти еще один, чтобы там никого не осталось. Но это уже не классика. Этот пример подводит нас к следующей главе о том, можно ли доверять здравому смыслу.

Назад: Мышление

Дальше: Ошибки мышления