Книга: Универсум. Общая теория управления
Назад: 4.3. ПФУ и причинно-следственные связи
Дальше: 4.5. Полное и сокращённое представление УФУ
4.4. ПФУ и динамическое программирование
Метод динамического программирования, является достаточно точным и подробным описанием действий по ПФУ, представленным в виде графа переходов (рис. 4.11). Основные положения метода, изложенные кратко, определяются следующим образом:
1) В задаче требуется найти последовательность шаговых управлений и траекторию, которой соответствует максимальный из возможных полных выигрышей. По своему существу полный “выигрыш” – это мера качества управления процессом в целом.2) Начальное состояние системы – «0» и множества её возможных последующих состояний – «1», «2», «3», а также возможные переходы из каждого возможного состояния в другие возможные состояния. Каждому переходу-шагу соответствует свой шаговый выигрыш, а в завершающем процесс третьем множестве – каждому из состояний системы придана его оценка, помещенная в прямоугольнике.3) В результате последовательного перебора множеств, при прохождении всего их набора, определяется оптимальная последовательность преемственных шаговых управлений, максимально возможный полный выигрыш и соответствующая им траектория, выделенная утолщённой линией. Критерий оптимальности – сумма шаговых выигрышей.4) Важно подчеркнуть, что метод динамического программирования работоспособен только, если определён вектор целей управления, т. е. если определено завершающее процесс состояние.«Каково бы ни было состояние системы перед очередным шагом, надо выбирать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным» [13, 109].
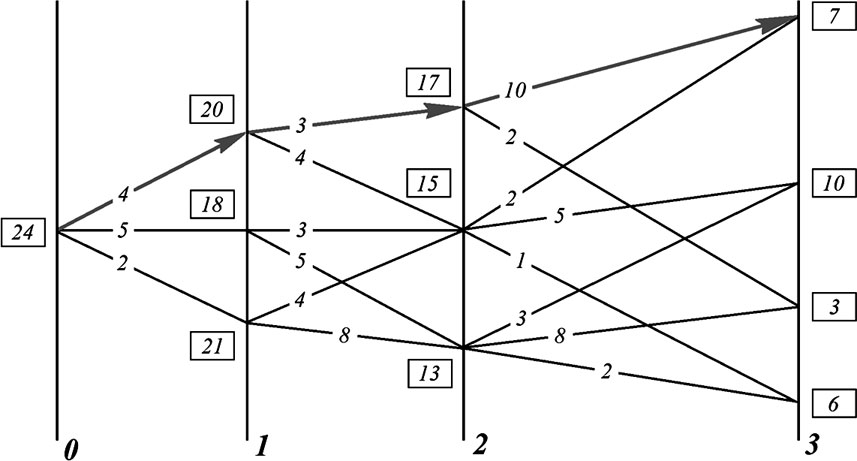
Рис. 4.11. Матрица возможностей метода динамического программирования.
В самом очевидном варианте интерпретации соответствие ПФУ методу динамического программирования выглядит просто (рис. 4.12).
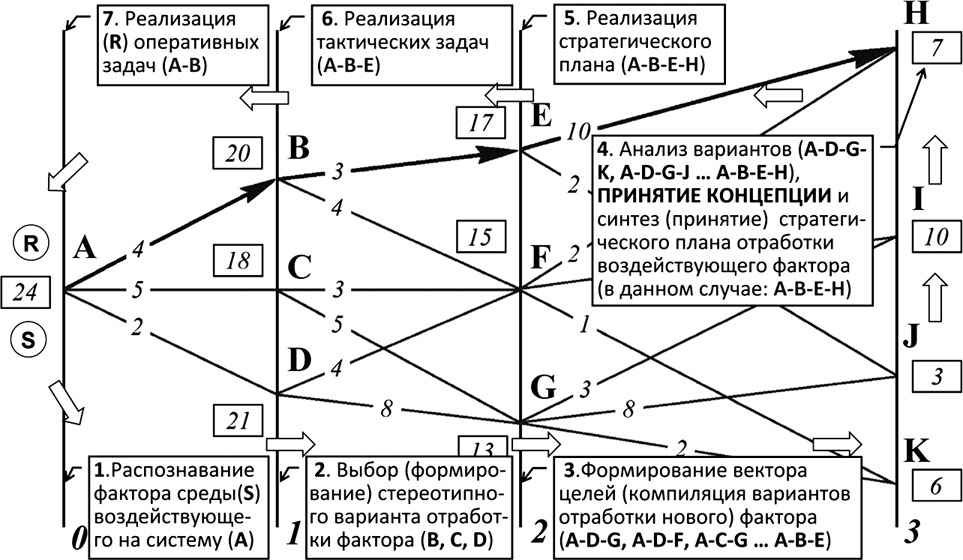
Рис. 4.12. Этапы ПФУ как варианты реализации матрицы возможностей
Определим фактор S, воздействующий на узел матрицы динамического программирования A матрицы переходов, или этап 1 ПФУ; варианты возможных стереотипных отработок фактора узлами, помеченными буквами B, С, D как шаг 1 или этап 2 ПФУ; варианты компилятивных решений (узлов комбинированных вариантов путей) буквами E, F, G как шаг 2 или этап 3 ПФУ и, наконец, конечные узлы состояний системы для всех возможных вариантов отработки фактора буквами H, I, J и К как шаг 3 или этап 4 ПФУ.
1-й этап ПФУ (Шаг 0): Для носящего однозначный (программный, конкретно распознанный в вершине А, характер воздействующего стимула S или отрабатывается сразу как реакция R (траектория S-1-А-7-R), или далее представляется как вариант выбора одного из готовых, стереотипных путей B, С, D отработки фактора на следующем шаге.
2-й этап ПФУ (Шаг 1): Если описываемая система обладает глубиной отслеживания ПСС в один шаг, то ей необходимо выбрать для отработки стимула S в виде реакции R один из возможных путей – B, C, D и затем возвратиться в точку А (траектория S-1–2-BCD-6–7-R). Для максимальной глубины прогностики в один шаг система выберет максимальный выигрыш 5, т. е. траекторию A-С.
Если система рассчитана на глубину отслеживания ПСС больше одного шага, то она перейдёт на следующий шаг расчётов.
3-й этап ПФУ (Шаг 2): Система начинает производить вариабельный расчёт различных путей попадания в узлы E, F, G. Здесь для определения максимального выигрыша необходимо просчитать все возможные сочетания путей А-В-Е, A-B-F, A-C-F … A-D-G. Это предикционный расчёт, в результате которого возникнет два варианта решения – пути A-C-G и A-D-G с выигрышем в 10 единиц. При максимальной глубине прогностики в два шага система выберет один из этих вариантов и вернётся в вершину А (траектория S-1–2-3-EFG-5–6-7-R) для отработки воздействующего фактора.
Если система рассчитана на глубину прогностики больше двух шагов, то она перейдёт на следующий шаг расчётов.
4-й этап ПФУ (Шаг 3): При максимальной глубине прогностики в три шага осуществится выработка единственной и окончательной траектории отработки фактора A-B-E-H с выигрышем 24 единицы. Это для описываемого смыслового поля – принятие максимально выигрышной стратегии решения проблемы, созданной воздействующим фактором, или, другими словами, принятие концепции отработки воздействующего на систему внешнего фактора (траектория S-1–2–3–4-H-5–6-7-R). Затем необходимо осуществить реализацию концептуального решения, которое «начинают с конца». Восходящий (здесь направленный вправо по шагам 0–1–2–3) U-поток закономерно переходит в нисходящий (т. е.направленный влево по шагам 3–2–1–0). Для представленных на схеме данных полученный в вершине H выигрыш составит 7 единиц.
5-й этап ПФУ (Шаг 2): Концепция реализуется в стратегическом плане действий, выраженном в выборе траектории A-B-E-H. Делается первый шаг реализации концепции по траектории Н-Е, на которой выигрыш составит 10 единиц. Общий выигрыш системы 7+10=17 единиц.
6-й этап ПФУ (Шаг 1): Продолжается реализация концепции, предусматривающей решение тактической задачи – движение по траектории E-B. Полученный выигрыш 17+3=20 единиц.
7-й этап ПФУ (Шаг 0): Решение оперативной задачи отработки фактора S в виде реакции R приносит системе выигрыш 20+4=24 единицы. ПФУ завершается выдачей в узле A выходного воздействия (реакции R), соответствующего входному стимулу S.
Этапы 5,6,7 ПФУ организуют стратегию, тактику и практическую реализацию принятой концепции управления, но, кроме этого, метод динамического программирования наглядно и просто поясняет, почему действия, реализующие стратегические планы, ограниченным частным сознанием иногда воспринимаются как неадекватные. Ведь с частнособственнической, имеющей ограниченный кругозор точки зрения такие действия не имеют нужного выигрыша в обозримом узком локальном пространстве шагов. Локальный кругозор не учитывает тот факт, что стратегические действия основаны на более приоритетном концептуальном уровне понимания процессов. Кроме того, очевиден и следующий вывод: выход систем на более высокий уровень прогностики требует не столько количественного, многократного, сколько качественного увеличения комбинаторной «расчётной мощности».
Для специалистов, привыкших использовать механические аналогии, рассмотренную схему динамического программирования можно также уподобить ручному манипулятору, имеющему в точке А рабочий SR-узел и состоящему из объединённых трёмя «соединениями» (¤) четырёх «плеч» (вершин A¤B¤E¤H), каждое из которых обеспечивает дополнительную степень свободы.
В таком представлении также будет вполне понятно, почему расчёт самого выигрышного пути следует вести последовательно, «начиная с конца», от общей концепции установки координат, т. е. от суммы координат всех плеч: ведь в общем случае неизвестно, какое из плеч окажет максимальное влияние на достижение цели, поставленной перед манипулятором. Максимально адекватная информированность о диапазонах перемещения манипулятора и ограничениях степеней свободы на каждом из шагов увеличивает точность расчёта выигрышной ситуации. Какая-то «незначительная», «невесомая» на первый взгляд, ограниченная степень свободы может определить вообще единственно возможную комбинацию координат рабочего узла манипулятора (точку А).
Здесь налицо явные параллели с сетевым планированием, выстраивающим график выполнения каких-то работ. Сетевой график, как инструмент планирования по ПФУ, это:
1. Определение тех элементов, которые должны входить в состав универсума;
2. Определение стандартных конструкций из элементов и порядка их сборки;
3. Проведение вариабельного (предикционного, оптимизационного) расчёта нестандартных элементов и конструкций;
4. Принятие максимально удовлетворяющей заданным критериям (сроки, стоимость и т. п.) концепции исполнения графика (утверждение плана);
5. Исполнение стратегического плана работ, долгосрочные поручения вовлечённым и подчинённым структурам;
6. Исполнение заданных стратегией тактических заданий;
7. Выполнение конкретных, оперативных задач в рамках тактического задания каждой из структур.
Описание той же алгоритмики выработки оптимального (специального) решения R для любой частной (специальной) задачи в привязке к этапам модели динамического программирования в виде импликативного описания ПФУ (рис. 4.13) позволяют определить алгоритмику выработки U-стратификационных качественных изменений и ответить на вопрос, почему переход к новому качеству имеет скачкообразный, многоступенчатый характер.
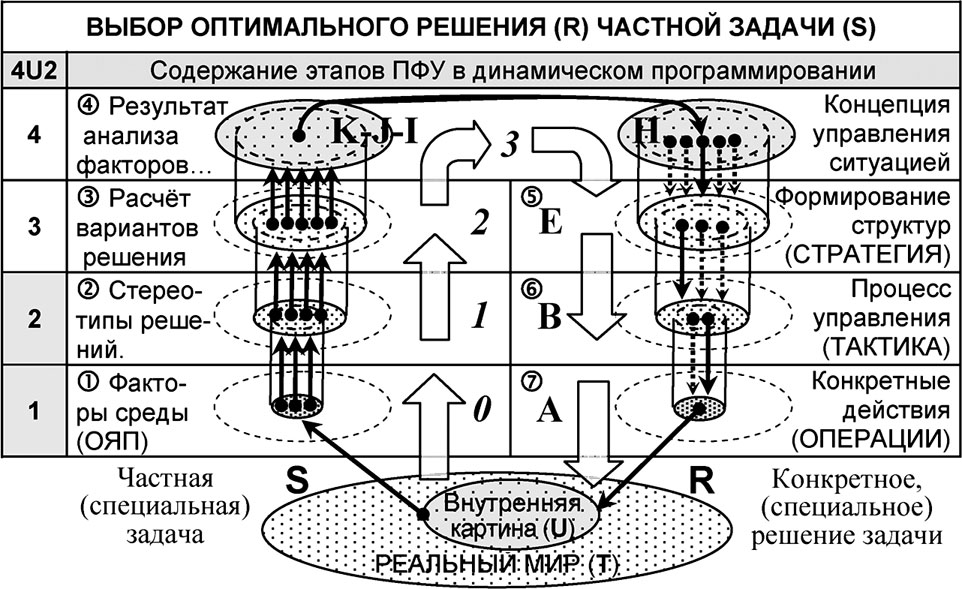
Рис. 4.13. Этапы ПФУ как объёмы логических множеств альтернатив в процессе решении частной задачи
Схема также позволяет пояснить некоторые философские открытия, причём сделать это не столько на основании интуитивных прозрений и многосложной гуманитарной цепи рассуждений, сколько на базе формальных логических операций.
Так, этапы отсчёта состояния системы в процессе динамического программирования (0–3), соответствуя U-стратам (1–4), можно представить плоскостями логических множеств, связанными для восходящего и нисходящего U-потока цепочкой импликативных отношений двух типов: «причина – возможные следствия» и «причина – выбранное следствие». Здесь из всего множества поступивших на вход S универсума комбинаций внешних факторов (этап 1 ПФУ) импликативно отбираются возможные стереотипные варианты решений (этап 2). Процесс импликации – ещё большего комбинаторного расширения вариантов решений (этап 3) развивается до максимального качественного «расширения» поля множеств (этап 4), на котором из всех возможных вариантов принимается «сужающее» – единственное, согласованное со всей предыдущей комбинаторикой, концептуальное (оптимальное для данного состояния U) решение. Затем процесс импликации развёртывает отработку стимула S в обратной последовательности (этапы 5, 6, 7), сужая множество возможных вариантов достижения концептуального решения до ограниченного спектра конкретных, последовательно исполняемых реакций R. В классической философской терминологии это описание соответствует понятиям «причинность» как порождение причиной S следствия R и «взаимодействие», как процесс порождения реакций R с учётом влияния на S цепей обратных связей [32, 58] универсумной модели.
Конечно же, логика выполнения этапов ПФУ и прохождения U-потока, представленного в виде имплицируемых множеств познания-практики, не ограничивается функциями импликации, дизъюнкции или конъюнкции, она гораздо богаче по содержанию и включает известные операции сравнения, селекции, анализа, синтеза и другие [41, 123].
Что же касается более общей алгоритмики работы познания, то в результате многолетней спонтанной работы философы пришли к достаточно определённым, хотя, опять же, «тройственным» выводам.
В философии Нового времени сложилась оппозиция сенсуализма и рационализма. Сенсуализм (от лат. sensus – чувство) решающую роль в познании отводил чувственному познанию. Рационализм (от лат. ratio – разум) решающую роль в познании отводил разуму…Оппозиция сенсуализма и рационализма ошибочна… Чувственное и логическое познание – самостоятельные способы познания и в то же время они взаимосвязаны, друг без друга не существуют. Хотя в деталях «механизмы» взаимосвязи чувственного и логического познания еще не изучены… [32,129].Представляется перспективным объяснение появления новых чувственных образов и понятий на основе взаимодействия чувственности и мышления. Новые чувственные образы возникают на основе опосредования имеющихся чувственных образов понятиями (так называемая эйдетическая интуиция); новые понятия возникают на основе опосредования имеющихся понятий чувственными образами (так называемая концептуальная интуиция). Эти опосредования тонки, трудно уловимы, происходят в сфере подсознания, вследствие чего и складывается мнение, что новые чувственные образы рождаются из имеющихся, новые понятия – тоже из имеющихся «само собой», спонтанно [32,131].
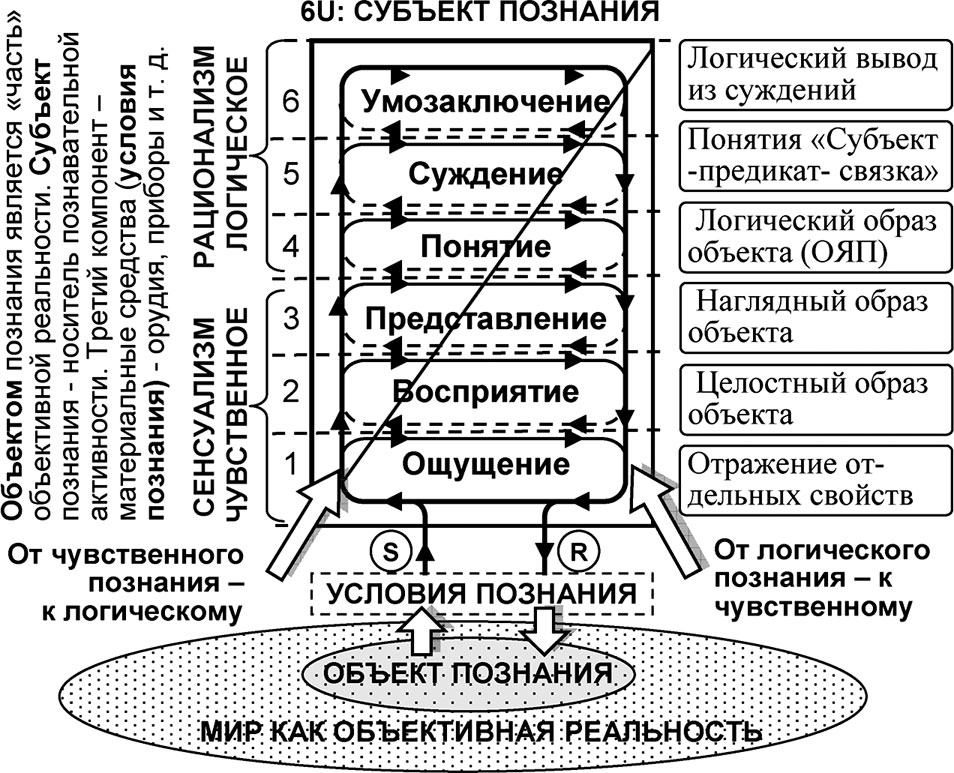
Рис. 4.14. Универсумное представление философских категорий познания
Выработанные гносеологией многочисленные и разрозненные конструкты можно представить единой схемой, например, класса 6U (рис. 4.14). Здесь простой U-схемой представлен весь комплекс классических субъектно-объектных взаимосвязей и взаимозависимостей между сенсуализмом, рационализмом и рядом конструктов познания, поддающихся не только чувственному, но уже и логическому анализу.
В результате процесса познания человек вырабатывает новые теории, которые в соответствии с принципом простоты также удобно представить в универсумном виде (рис. 4.15).
Теория как система знаний характеризуется рядом признаков.Предметность. Вся совокупность понятий и суждений конкретной теории должна относиться к определенной предметной области…Адекватность и полнота описания. Предложения теории могут описывать все существующие ситуации в предметной области теории.Интерпретируемость. Все понятия теории должны быть интерпретируемы, выявлено их объективное содержание.Проверяемость. Должна быть возможность установления соответствия теории свойствам и отношениям объектов ее предметной области.Иногда предлагают признак простоты: как отсутствие излишних искусственных построений в теории.
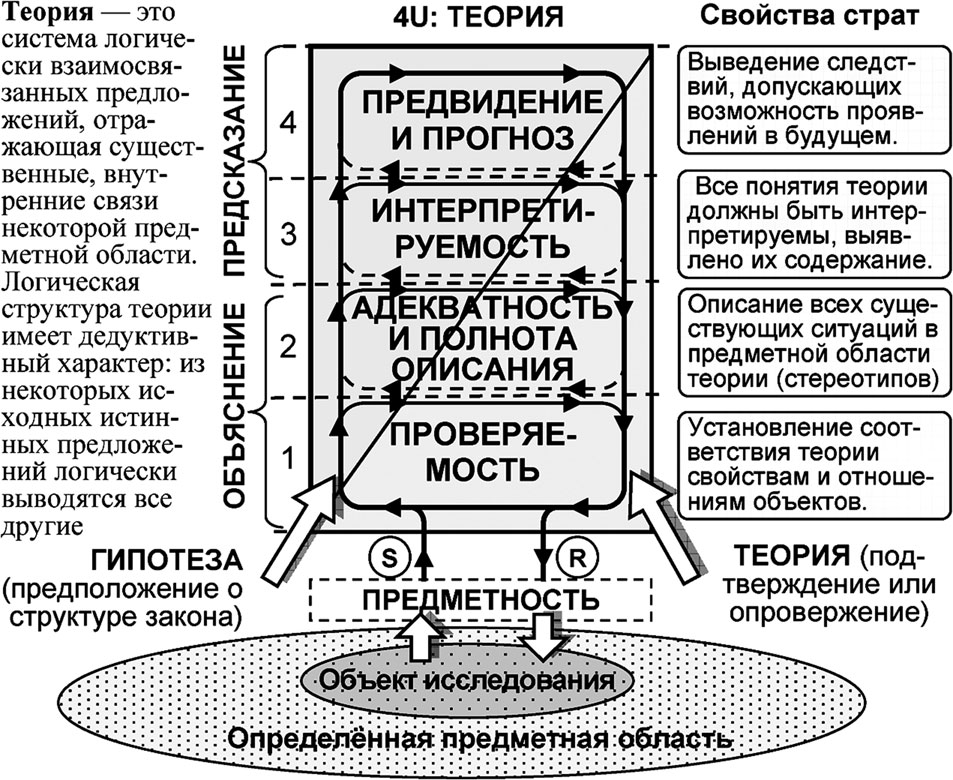
Рис. 4.15. Универсумное представление философской категории «теория»
Теория выполняет две основные функции: объяснения и предсказания. Предсказание заключается в выведении из теории следствий, допускающих возможность таких фактов и законов, которые существуют, но неизвестны, или таких событий, которые могут произойти в будущем [32, 155].
Универсумное представление позволяет не только видеть целостную картину реализации процесса «от гипотезы – к теории» как целостный комплекс сложных взаимосвязей философских категорий познания, но и дополнить классический философский подход новыми и даже полезными выводами и открытиями.

