Книга: Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.
Назад: Глава 20. Риманов оператор и другие подходы
Дальше: Глава 22. Она или верна, или нет
Глава 21. Остаточный член
I.
В главе 19 мы определили ступенчатую функцию J, выразив ее через функцию π, которая подсчитывает для нас простые числа, а потом использовали мебиусово обращение, чтобы выразить π через J. Повернув затем Золотой Ключ, мы шаг за шагом прошли по тем вычислениям, с помощью которых Риман выразил дзета-функцию ζ через функцию J. А другое обращение, как я сказал, позволит выразить J через ζ. Сухой остаток всего этого таков.
• Функцию π, которая пересчитывает простые числа, можно выразить через другую ступенчатую функцию J.
• Функцию J оказывается возможным выразить через дзета-функцию Римана ζ.
Отсюда получается, что все свойства функции распределения простых чисел π некоторым образом закодированы в функции ζ. Достаточно тщательное исследование свойств функции ζ подскажет нам все, что мы хотим узнать про функцию π, другими словами, про распределение простых чисел.
Как же все это на самом деле работает? Какова программа действий? Где в ней найдется место тем самым нетривиальным нулям? И как выглядит этот «посредник» — функция J — когда он переписан через функцию ζ? Ответ на последний вопрос я замял в конце главы 19.
II.
Я замял ответ на этот вопрос по вполне уважительной причине, которая сейчас станет ясной. Выражение (21.1) содержит результат этого второго обращения, окончательное и точное выражение функции J(x) через дзета-функцию:
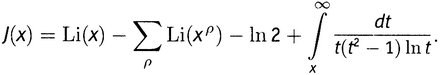
Вот с чем предстоит иметь дело. Если вы не математик, то перед вами — страшный монстрик (и где, кстати, в нем сидит дзета-функция?). Я собираюсь разобрать эту штуку на кусочки, один за другим, и показать, что творится у нее внутри. Но прежде всего сообщу, что это равенство и составляет основной результат статьи Римана 1859 года. Если вы сможете его одолеть, то поймете суть того, что сделал Риман в этой области, и получите ясное представление обо всем, что было после.
Первое, что надлежит заметить, — это что правая часть выражения состоит из четырех частей, или членов. Первый член, Li(x), носит общее название главного члена. Про второй член, имеющий вид ∑ρLi(xρ), Риман говорил во множественном числе как о «периодических членах» (periodischer Gleider) — по причинам, которые вскоре выяснятся; мы будем говорить о нем в единственном числе как о «вторичном члене». Третий член в нашей формуле — дело нехитрое. Это просто число, ln 2, равное 0,69314718055994…
С четвертым членом, несмотря на страх, который он наводит на нематематиков, разобраться на самом деле несложно. Он представляет собой интеграл, т.е. площадь под кривой, описывающей некоторую функцию, причем площадь вычисляется от аргумента x и аж до самой бесконечности. Функция здесь — это, разумеется, 1/(t(t2 − 1)ln t). Нарисовав ее график (рис. 21.1), мы убеждаемся, что она очень даже отзывчива в отношении того, чего мы от нее хотим. Надо только помнить, что нас совершенно не волнуют значения аргументах, меньшие 2, поскольку J(x) равна нулю, когда x меньше двойки. Поэтому при x = 2 показанная на рисунке затемненная область — это максимальное значение, которого вообще может достигать этот интеграл (т.е. четвертый член в формуле). Площадь затемненной области, т.е. максимальное значение четвертого члена при любых x, которые вообще могут нас интересовать, составляет в действительности 0,1400101011432869….

Рисунок 21.1. Четвертый член в выражении Римана для J(x).
Таким образом, взятые вместе (с учетом знаков) третий и четвертый члены ограничены интервалом от −0,6931… до −0,5531…. Поскольку изучаемая нами функция π(x) по-настоящему интересна только для миллионов и триллионов, эффект от этих двух членов невелик, так что мы практически ничего не будем о них говорить, а сконцентрируемся на двух первых членах.
Главный член тоже не представляет особой проблемы. В главе 7.viii мы уже определили функцию Li(x) как площадь под кривой 1/ln t, измеряемую от нуля до x; мы также привели Теорему о распределении простых чисел (ТРПЧ) в виде π(N) ~ Li(N). В нашем главном члене x — вещественное число, а потому значение Li(x) можно взять из математических таблиц или же вычислить с помощью любой нормальной математической программы, типа Maple или Mathematica.
Разобравшись таким образом с первым, третьим и четвертым членами в выражении , мы сфокусируемся на втором, имеющем вид ∑ρLi(xρ). В нем — корень происходящего, и дело тут нешуточное. Сначала я в общих чертах расскажу, что он означает и как он попал в выражение . А потом разберу его на части и покажу, почему он играет ключевую роль для понимания распределения простых чисел.
III.
Знак ∑ — это приглашение к тому, чтобы суммировать, т.е. складывать многое в одно. На множество, по которому производится суммирование, указывает маленькая буква ρ под знаком ∑. Эта буква — не латинская p, а ро — семнадцатая буква греческого алфавита, причем в данном случае она фигурирует в значении «корень». Для вычисления этого вторичного члена надо сложить друг с другом Li(xρ) для всех корней, по очереди придавая букве ρ значение, равное каждому из корней. Что это, кстати говоря, за корни? Ясное дело, ведь это нетривиальные нули дзета-функции Римана!
Как же все эти нули попали в выражение для J(x)? Объяснить это я могу лишь в общих чертах. Вспомним выражение, которое мы, повернув Золотой Ключ, получили в главе 19:

Мы говорили, что у математиков есть способ обратить это выражение — вывернуть его наизнанку, т.е. выразить J(x) через дзета-функцию. Процедура обращения в действительности и длинна, и сложна; в большинстве из составляющих ее шагов задействована математика, выходящая за рамки того, что приводится в этой книге. Поэтому-то я и перескочил прямо к окончательному результату — выражению . Тем не менее, как мне кажется, я в состоянии объяснить одну часть этой процедуры. Дело в том, что один шаг в этом обращении заключается как раз в выражении дзета-функции через ее нули.
Сама по себе идея выражения функций через их нули не несет в себе особой новизны для тех, кто изучал алгебру в старших классах. Рассмотрим старые добрые квадратные уравнения, выбрав в качестве примера то, которое мы использовали в главе 17.iv, а именно z2 − 11z + 28 = 0 (однако будем писать букву z вместо x, поскольку сейчас мы находимся в царстве комплексных чисел). Левая часть этого уравнения, разумеется, представляет собой функцию, причем полиномиальную функцию (т.е. многочлен). Если мы подставим в нее любое значение аргумента z, то после выполнения определенных арифметических действий получим значение функции. А если, скажем, мы подставим аргумент 10, то значением функции будет 100 − 110 + 28, что дает 18. Если подставим аргумент i, то значением функции будет 27 − 11i.
А каковы решения уравнения z2 − 11z + 28 = 0? Как мы видели в главе 17, это 4 и 7. При подстановке любого из этих чисел в левую часть уравнение превращается в верное равенство, поскольку левая часть оказывается равной нулю. Другой способ выразить то же самое — это сказать, что 4 и 7 являются нулями функции z2 − 11z + 28.
Теперь, зная нули, мы можем разложить эту функцию на множители. Она разлагается на множители как (z − 4)(z − 7). По правилу знаков это можно записать и как (4 − z)(7 − z). Еще один способ записи — это 28(1 − z/4)(1 − z/7). Смотрите: так или иначе, мы выразили функцию z2 − 11z + 28 через ее нули! Разумеется, такое можно делать не только для квадратичных функций. Многочлен пятой степени z5 − 27z4 + 255z3 − 1045z2 + 1824z − 1008 тоже можно записать через его нули (каковыми являются числа 1, 3, 4, 7, 12). Вот как: −1008(1 − z/1)(1 − z/3)(1 − z/4)(1 − z/7)(1 − z/12). Любую полиномиальную функцию можно переписать через значения ее нулей.
Полиномиальные функции обладают интересным свойством с точки зрения теории функций комплексной переменной. Область определения полиномиальной функции составляют все комплексные числа. Полиномиальная функция никогда не «обращается в бесконечность». Нет такого значения аргумента z, при котором оказалось бы невозможным вычислить ее значение. При вычислении значения полиномиальной функции для любого заданного значения аргумента используются только возведение аргумента в положительные целые степени, умножение этих степеней на числа и сложение полученных результатов друг с другом. Такое можно проделать со всяким числом.
Функции, область определения которых составляют все комплексные числа и которые ведут себя достаточно симпатичным образом (для чего имеется точное математическое определение!), называются целыми функциями. Все полиномиальные функции — целые. Показательная функция — тоже целая. Однако рациональные функции, которые мы рассматривали в главе 17.ii, не целые, потому что знаменатели в них могут обращаться в нуль. Функция ln также не является целой: у нее нет значения при нулевом аргументе. Подобным же образом у дзета-функции Римана нет значения при аргументе, равном единице, а потому она не является целой функцией.
Целая функция может не иметь нулей вовсе (как, например, показательная функция: равенство ez = 0 никогда не выполняется), может иметь их несколько (как, например, полиномиальные функции: числа 4 и 7 — нули функции z2 − 11z + 28), а может — бесконечно много (как, например, синус, который обращается в нуль при всех целых кратных числа π). Ну и раз полиномиальные функции выражаются через свои нули, интересно, можно ли все целые функции выразить подобным же образом? Пусть у нас есть какая-нибудь целая функция — назовем ее F, — определяемая бесконечной суммой вида F(z) = a + bz + cz2 + dz3 + …, и пусть еще нам удалось узнать, что у этой функции бесконечно много нулей; назовем их ρ, σ, τ, …. Можно ли выразить данную функцию через ее нули, в виде бесконечного произведения F(z) = а(1 − z/ρ)(1 − z/σ)(1 − z/τ)… — как если бы бесконечная сумма была чем-то вроде «сверхмногочлена»?
Ответ таков: да, при определенных условиях можно. И когда такое удается сделать, получается, как правило, чрезвычайно полезная штука. Например, именно таким способом — применив подобное рассуждение к синусу — Эйлер и решил базельскую задачу.
Но какая нам польза от всего этого для дзета-функции, которая, увы, не является целой функцией? Дело в том, что в ходе упомянутой выше сложной процедуры обращения Риман преобразовал дзета-функцию в нечто слегка от нее отличающееся — в целую функцию, нули которой суть в точности нетривиальные нули дзета-функции. И эту-то слегка измененную функцию можно выразить через данные нули. (Тривиальные нули спокойно исчезли в ходе преобразования.)
Таким вот образом, после некоторой дополнительной обработки, в конце концов и получается выражение ∑ρLi(xρ), в котором сумму надо брать по всем нетривиальным нулям дзета-функции.
И теперь, чтобы продемонстрировать важность вторичного члена в выражении , а также связанные с ним проблемы, мы разберем его на части. Для этого начнем с его сердцевины и будем двигаться изнутри наружу, т.е. сначала рассмотрим xρ, затем функцию Li, а потом уже — вопрос о суммировании по всем возможным значениям буквы ρ.
IV.
Вот, стало быть, перед нами число x, являющееся вещественным. (Окончательная цель всего упражнения состоит в том, чтобы получить формулу для функции π(x), а она осмысленна только для вещественных чисел и даже, честно говоря, для натуральных; правда, мы изменили обозначения от N к x, чтобы использовать средства математического анализа.) С этим x мы делаем такое: возводим его в степень ρ, представляющую собой комплексное число, причем если Гипотеза Римана верна, то комплексное число вида 1/2 + ti (где t — некоторое вещественное число). Это действие само по себе заслуживает обсуждения.
При возведении вещественного числа x в комплексную степень а + bi правила комплексной арифметики предписывают следующее. Модуль результата — т.е. расстояние до нуля, измеряемое по прямой, — есть xa. Буква b на модуль никак не влияет. Зато фаза результата — насколько он повернут и в каком секторе комплексной плоскости лежит — зависит от x и b, но a на фазу не влияет.
При возведении вещественного числа x в степень 1/2 + ti, таким образом, модуль результата есть x в степени 1/2, т.е. √x. Фаза при этом может оказаться какой угодно — результат может угодить в любой сектор комплексной плоскости, при условии только, что расстояние от нуля равно √x. Иными словами, если при заданном x вычислять значения выражения xρ для множества различных нулей ρ дзета-функции, то получаемые числа будут разбросаны по окружности радиуса √x в комплексной плоскости с центром в нуле (при условии, что ГР верна!).
На рисунке 21.2 отмечены точки, представляющие собой результат возведения числа 20 в степень, определяемую первым, вторым, третьим, …, двадцатым нулем дзета-функции. Видно, что результаты разбросаны по окружности радиуса √20 (что равно 4,47213…) в комплексной плоскости, причем без особого порядка. Это происходит потому, что функция 20s отображает критическую прямую в окружность радиуса √20 таким образом, что критическая прямая (вместе со всеми нанесенными на нее нулями дзета-функции) наматывается и наматывается на эту окружность, делая это бесконечное число раз. На математическом языке данная окружность в плоскости значений задается как 20критическая прямая.

Рисунок 21.2. Плоскость значений для функции w = 20z. Показаны значения w для первых двадцати нетривиальных нулей дзета-функции.
Представим себе, что наш приятель муравей Арг топает на север по критической прямой в плоскости аргумента, а на его приборчике выставлена функция 20s; тогда его брат-близнец, муравей Знач, отслеживая соответствующие значения в плоскости значений, нарезает круги по нашей окружности. Он продвигается против часовой стрелки, и к тому моменту, как муравей Арг доберется до первого нуля дзета-функции, муравей Знач одолеет уже почти три четверти своего седьмого круга.
V.
А теперь мы найдем, одно за одним, значения функции Li во всех этих точках — во всем бесконечном числе этих точек. К сожалению, это комплексные числа, а мы определили функцию Li только для вещественных чисел — как площадь под кривой. Имеется ли способ определить Li также и для комплексных чисел? Что из себя представляют интегралы для комплексных чисел? Да, способ определить эту функцию есть; и, кроме того, да, существует способ интегрировать, когда в этом деле участвуют комплексные числа. Интегрирование на самом деле представляет собой один из важнейших элементов комплексного анализа, объект самых прекрасных и мощных теорем во всем этом разделе. Не вдаваясь в подробности, я скажу только, что, да, функция Li(z) определена для комплексных чисел z.
На рисунке 21.3 показано, куда функция Li отображает первые 10 точек, изображенных на рисунке . Другими словами, (точнее, ее отрезок от 1/2 + 14i до 1/2 + 50i). Как видно, эта функция отображает критическую прямую в спираль, идущую против часовой стрелки и приближающуюся к числу πi по мере того, как аргумент взбирается вверх по критической прямой. Там, где функция 20z бесконечно много раз наматывала и наматывала критическую прямую на окружность радиуса √20, применение функции Li разматывает ее в изящную спираль; на ней по-прежнему нарисованы точки, изображающие нули.
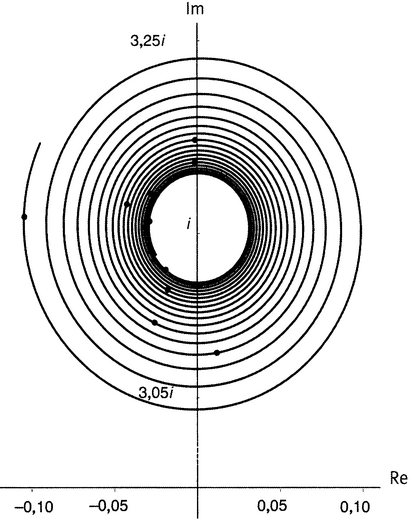
Рисунок 21.3. Функция Li(20z) для отрезка критической прямой.
VI.
Теперь примемся за знак сигмы, где надо суммировать эти точки (каждая из которых — просто комплексное число) по всем возможным нетривиальным нулям дзета-функции. Для этого сначала вспомним один момент, который мы до сих пор практически игнорировали. Для каждого нетривиального нуля, расположенного на северной половине критической прямой, имеется соответствующий нуль на ее южной части. Если, например, 1/2 + 14,134725i — нуль дзета-функции, то нулем должно быть и число 1/2 − 14,134725i. На чисто математическом языке можно сказать, что если z — нуль, то и его комплексное сопряжение z' также есть нуль. (Мы помним, что z' произносится как «зет-с-чертой». Сейчас может оказаться нелишним взглянуть на рисунок и освежить в памяти основные факты о комплексных числах.)
При выполнении суммирования южная часть критической полосы играет ключевую роль. На рисунках и были показаны лишь первые несколько нулей вдоль северной половины критической прямой. Для создания более полной картины, включающей и южную половину этой прямой, в самой левой части рисунка 21.4 показана плоскость комплексных чисел с отмеченной критической полосой от 1/2 − 15i до 1/2 + 15i. Этого достаточно, чтобы был виден первый нуль при 1/2 + 14,134725i, а также его комплексное сопряжение 1/2 − 14,134725i. Они отмечены буквами ρ и ρ'.
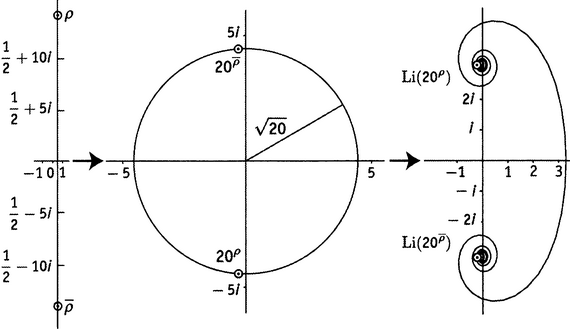
Рисунок 21.4. Критическая прямая, продолженная до первой пары нетривиальных нулей, и ее отображение сначала с помощью функции 20z, а затем с помощью функции Li(20z).
Рассматривая эту плоскость как плоскость аргумента для функции 20z, мы получаем на средней части рисунка картинку типа «сюда» в плоскости значений — окружность радиуса √20, где, как и на рисунке , отмечено 20ρ, а наряду с этим отмечено еще и 20ρ'. Заметим, что, когда аргументы комплексно сопряжены друг другу, сопряжены и значения функции. Такое происходит не со всеми функциями, но, по счастью, происходит с функцией 20z. Если мы применим функцию Li, на этот раз используя в качестве ее плоскости аргумента среднюю часть рисунка , то мы увидим, что критическая прямая, которая намоталась на эту окружность бесконечное число раз под действием функции 20z, теперь разматывается в симпатичную двойную спираль в правой части рисунка. (Рисунок представлял собой «наезд камеры» на верхнюю часть этой спирали.) И по-прежнему, когда аргументы комплексно сопряжены друг другу, сопряжены и значения.
Осталось заметить еще только одну вещь перед тем, как мы приступим к сумме ∑ρLi(20ρ). Показанная спираль — что лучше всего видно из рисунка — стремится к точке своего назначения не слишком быстро. Скорость, с которой она сходится, по сути дела гармоническая: если представить себе, что муравей Арг шагает на север по критической прямой, а на его приборчике выставлена функция Li(20ρ), то муравей Знач будет двигаться по спирали, постепенно приближаясь к точке πi — приближаясь на расстояние, обратно пропорциональное высоте, на которую забрался муравей Арг. Если последний вскарабкался на высоту T, то муравей Знач будет находиться от точки πi примерно на расстоянии, пропорциональном 1/T.
Имея это в виду, мы теперь готовы взяться за сумму ∑ρLi(20ρ). Сложению подлежат комплексные числа, соответствующие всем нашим точкам на спирали, изображенной на рисунке , а также их комплексно сопряженным точкам на соответствующей южной части спирали. Поскольку для каждой точки северной спирали имеется ее зеркальное отображение на южной, все мнимые части сократят друг друга: для каждого a + bi найдется соответствующее a − bi, так что при их сложении получится просто 2a. Ну и отлично, потому что J(x) — вещественное число, и решительно не годится иметь мнимые слагаемые в правой части выражения ! Это и вправду хорошая новость, потому что она означает, что складывать надо только вещественные (т.е. западно-восточные) части точек на рисунке . Вклад южного полушария сводится просто к тому, что ответ удваивается, т.е. (a + bi) + (a − bi) = 2а.
Остальные новости похуже. Точки, раскиданные по спирали на рисунке , как уже было замечено, сходятся к числу πi — а их вещественные части, стало быть, сходятся к нулю — с гармонической скоростью. Сложение вещественных частей всех этих точек, следовательно, чревато опасностью, что мы будем складывать нечто вроде гармонического ряда, который, как мы помним из главы 1, расходится. Откуда нам знать, что сумма ∑ρLi(20ρ) сходится?
Делу помогает тот факт, что вещественные части этих точек то положительны, то отрицательны. На самом деле наша сумма похожа не на гармоническую сумму, а на ее близкого родственника, с которым мы бегло встречались в главе 9.vii:
1 − 1/2 + 1/3 − 1/4 + 1/5 − 1/6 + 1/7 − …
Слагаемые здесь приближаются к нулю гармонически: 1, 1/2, 1/3, 1/4, 1/5, …, но чередующиеся знаки плюс и минус означают, что каждый следующий член до некоторой степени сокращает предыдущий, что и приводит к сходимости. Но эта сходимость, если использовать введенную в главе 9.vii терминологию, лишь условна. Она зависит от суммирования всех членов в правильном порядке.
Так же обстоит дело и с рядом ∑ρLi(20ρ). Если мы желаем обеспечить сходимость к правильному числу, то нам следует проявлять осторожность относительно порядка суммирования. Так каков же правильный порядок? Он ровно такой, как вы и подумали. Берем нули один за другим, двигаясь вверх по критической прямой, и прибавляем к каждому его комплексно-сопряженный нуль из южной части.
VII.
Итак, для вычисления суммы ∑ρLi(20ρ) мы сначала складываем каждый нуль дзета-функции с его зеркальным образом (т.е. с комплексным сопряжением) из южной половины плоскости аргумента. Далее эти пары надо сложить в порядке возрастания положительных мнимых частей. Таким образом, мы складываем нули в следующем порядке:
1/2 + 14,134725i и 1/2 − 14,134725i; затем
1/2 + 21,022040i и 1/2 − 21,022040i; затем
1/2 + 25,010858i и 1/2 − 25,010858i; затем ….
Чтобы посмотреть, что же получается в результате этого процесса, и разобраться в том, почему Риман назвал этот вторичный член «периодическими членами», поупражняемся немного в арифметике, используя конкретные значения буквы x. Как и раньше, возьмем x = 20; тем самым мы вычисляем величину J(20) — что, как несложно проверить из исходного определения функции J, равно 97/12 т.е. 9,5833333…. Вот как это получается.
Сначала возводим 20 в степень 1/2 + 14,134725i. В результате получаем точку, которая на рисунке помечена как 1 и численно выражается как −0,302303 − 4,46191i. Интегральный логарифм от этого — т.е. функция Li — дает самую западную точку на рисунке , выражаемую числом −0,105384 + 3,14749i. Теперь разберемся с сопряженным членом из этой пары нулей. Возводим 20 в степень 1/2 − 14,134725i. Результат равен −0,302303 + 4,46191i. Он показан на средней картинке на рисунке . Это зеркальный образ точки, помеченной на рисунке как 1, относительно вещественной оси. Берем интегральный логарифм и получаем ответ −0,105384 − 3,14749i — точку, лежащую глубоко на юге в правой части рисунка . Складывая два ответа, получаем −0,210768. Мнимые части, разумеется, сократились. Вот и все с первой парой сопряженных нулей.
Повторим все это для второй пары, 1/2 + 21,022040i и 1/2 − 21,022040i. На этот раз окончательный ответ будет равен 0,0215632. Для третьей пары он равен −0,0535991. С тремя парами мы разобрались, но впереди бесконечность!
После 50 таких вычислений получаем (таблицу следует читать по колонкам):
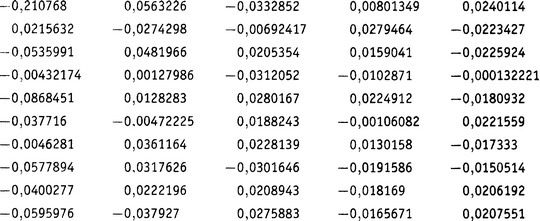
Первое значение представляет собой некоторую аномалию, поскольку самая западная точка на рисунке отстоит от вертикальной оси более чем в два раза дальше, чем остальные. Однако затем числа в таблице уменьшаются по мере того, как значения, соответствующие северной половине критической прямой, по спирали приближаются к πi. И взгляните на их знаки — имеется примерно равное число положительных и отрицательных. Это хорошая новость, потому что, хотя ответы и становятся меньше, они делают это не очень быстро, и нам потребуется вся возможная помощь, которую могут нам оказать сокращения между положительными и отрицательными значениями. Не будем забывать, что все это происходит под знаком суммы — эти 50 чисел предстоит еще сложить друг с другом. (Сумма равна −0,343864, что, кстати, составляет не более 8 процентов от полной бесконечной суммы. Не так плохо для всего лишь 50 слагаемых.)
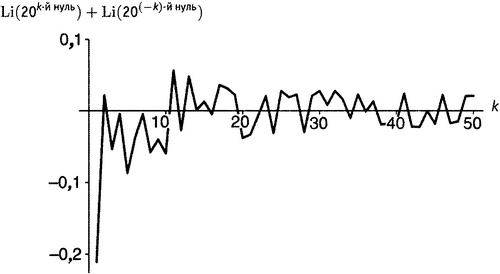
Рисунок 21.5. Первые 50 значений, полученных путем взятия нетривиального нуля и его комплексно сопряженного, вычисления значений функции Li(20z)и их последующего суммирования.
Из рисунка 21.5 видно, почему Риман назвал эти компоненты вторичного члена «периодическими». Они изменяются нерегулярным образом (что означает, если уж быть совсем скрупулезным, что они не строго «периодические», а только «колебательные») вверх и вниз от положительных к отрицательным значениям и обратно. Причина этого совершенно ясна из рисунка . Колебательная природа вторичных членов связана с тем, что, как видно из рисунка , функция Li(xρ) скручивает критическую прямую во все более и более плотную спираль. Значения функции, соответствующие нулям дзета-функции, могут при этом оказаться где угодно на этой спирали; определяющая причина состоит в том, что для больших x критическая прямая чрезвычайно сильно растягивается перед закручиванием. Закручивание настолько плотное, что высоко расположенный отрезок критической прямой отображается в нечто очень близкое по форме к окружности. В силу этого получается, что значения функции Li(xρ) в нулях дзета-функции выглядят примерно как точки, раскиданные по окружности. Если вы немного знакомы с тригонометрией, то вам известно, что это приводит нас в мир синусов и косинусов, волновых функций, колебаний, вибраций… музыки. Именно отсюда и взялось введенное сэром Майклом Берри понятие «музыка простых чисел».
По мере прибавления новых членов сами они убывают, а положительные и отрицательные до некоторой степени сокращают друг друга при суммировании, так что мы зарабатываем сходимость. Эта сходимость, правда, страшно медленная. Для получения результата с точностью в три значащие цифры приходится складывать более 7000 членов; в четыре цифры — более 86 000. На графике на рисунке 21.6 показаны первые 1000 результатов (хотя некоторые из самых левых при выбранном масштабе оказались за пределами рисунка); на этот раз не делается никаких попыток соединить точки между собой. Видно, что члены под знаком суммы действительно уменьшаются, хотя и делают это с достаточной ленцой.
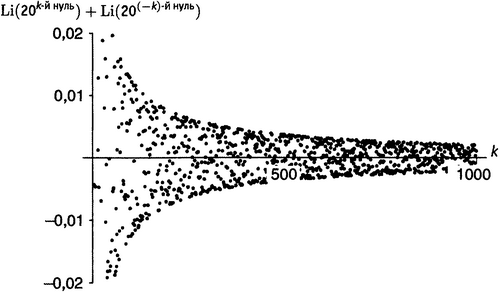
Рисунок 21.6. То же, что на рисунке , но показана 1000 значений (точки не соединены между собой).
Окончательный результат равен −0,370816425…. Это, как мы помним, второй член в выражении . Первый же член — это в нашем случае Li(20), равный 9,90529997763…. Третий равен ln 2, что составляет 0,69314718055994…. И четвертый член, тот самый надоедливый интеграл, добавляет пустячный результат 0,000364111…. Подставим все это в выражение и — хлоп! — J(20) = 9,58333333… (что мы, конечно, и так знали).
VIII.
Закончим тем, что с использованием формулы Римана проведем полное вычисление π(1000 000) — т.е. числа простых чисел в пределах одного миллиона — не ради веселья, хотя веселье и немалое, а для того, чтобы сделать несколько важных замечаний по поводу остаточного члена.
Как мы помним из главы 19.iv,
π(1000 000) = J(1000 000) − 1/2J(√1000 000) − 1/3J(3√1000 000) − ….
Сколько же членов в правой части надо вычислять? До тех пор пока числа в скобках не станут меньше 2, потому что J(x) равна нулю, когда x меньше 2. Корень девятнадцатой степени из 1000 000 равен 2,069138…, а корень двадцатой степени 1,995262… Следовательно, можно остановиться на 19. Поскольку число 19 свободно от квадратов и имеет только один простой делитель — самого себя, — функция Мебиуса μ(19) имеет значение −1. Таким образом, последний член в правой части равен −1/19J(19√1000 000). Всего в правой части будет 13 слагаемых, поскольку между 1 и 19 функция Мебиуса принимает ненулевые значения 13 раз — при аргументах 1, 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19. Напомним, что функция Мебиуса равна нулю всякий раз, когда аргумент делится на точный квадрат (например, 4 или 9).
Каждое из этих 13 слагаемых состоит из четырех членов: главный член, вторичный член (куда и входят нули дзета-функции), член с ln 2 и интегральный член. Если сложить все эти 52 куска, получится π(1000 000) — число, про которое мы заранее знаем из главы 3.iii, что оно равно 78 498.
Вся эта арифметика расписана в таблице 21.1 (там опущены строки с N, для которых J(N) равно нулю). Двигаясь вдоль строки N и используя y для обозначения N-го корня из одного миллиона, имеем главный член 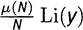 , вторичный член
, вторичный член  , член с ln 2, равный
, член с ln 2, равный  , и интегральный член
, и интегральный член 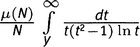 . Суммы по строкам должны быть равны — и в самом деле равны — выражению (μ(N)/N)J(y).
. Суммы по строкам должны быть равны — и в самом деле равны — выражению (μ(N)/N)J(y).
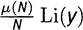 , вторичный член
, вторичный член  , член с ln 2, равный
, член с ln 2, равный  , и интегральный член
, и интегральный член 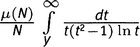 . Суммы по строкам должны быть равны — и в самом деле равны — выражению (μ(N)/N)J(y).
. Суммы по строкам должны быть равны — и в самом деле равны — выражению (μ(N)/N)J(y).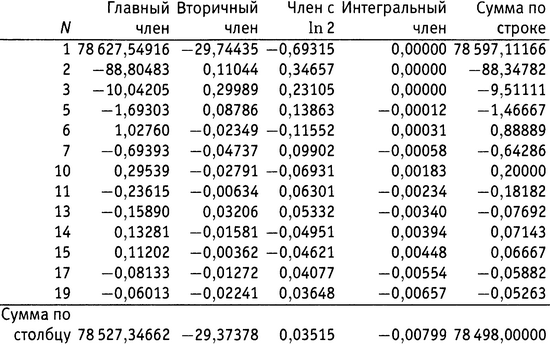
Таблица 21.1. Вычисление π(1000 000).
В качестве простой проверки возьмем строку с N = 6. Поскольку миллион — это 106, корень шестой степени из миллиона — это просто 10. Значение J(10) легко посчитать — оно оказывается равным 16/3. Поскольку число 10 свободно от квадратов и представляет собой произведение двух простых чисел, функция Мебиуса μ(10) имеет значение +1. Итак, в строке с N = 6 последний столбец должен быть равен (+1)×(1/6)×(16/3). Это составляет 8/9, что и говорится в суммарной колонке для строки с N = 6.
При N = 1 главный член, равен просто Li(1000 000); именно такое приближение к точному ответу дает нам ТРПЧ. Какова же разница между этим приближением и π(1000 000)? Ответ получается мгновенно путем простого вычитания: разность, вычисленная как π(1000 000) минус Li(1000 000) (чтобы сохранить знаки в нашей таблице), равна −129,54916. Из чего эта разница слагается?
Вот из чего:
| из главных членов | −100,20254 |
| из вторичных членов | −29,37378 |
| из членов с ln 2 | 0,03515 |
| из интегральных членов | −0,00799 |
Наибольший вклад в разницу дают главные члены. Однако эти члены вполне предсказуемы — они убывают быстро и неуклонно.
Разница, возникающая из вторичных членов, имеет тот же порядок величины, однако составляющие ее компоненты — те самые вторичные члены — вызывают куда больше беспокойства. Первый вторичный член достаточно велик и отрицателен; правда, нет никаких очевидных причин, почему он должен оказаться именно таким. Но и другие не очень помогают. Если просто двигаться вниз вдоль колонки с вторичными членами, не обращая внимания на знаки минус, а следя только за тем, будет ли каждый следующий член больше или меньше предыдущего по величине, то мы увидим такое: меньше, больше, меньше, меньше, больше, меньше, меньше, больше, меньше, меньше, больше, больше. Вторичный член при N = 19 оказывается почти таким же, как и при N = 6. Все эти вторичные члены — члены, которые выражаются через нули дзета-функции, — джокеры в нашем вычислении. А члены с ln 2, как и было обещано, несущественны.
Вспомним о статье Литлвуда 1914 года (см. главу 14.vii), где он доказал, что неверно утверждение, что Li(x) всегда превосходит π(x). Это означает, что разность рано или поздно станет положительной. Поскольку главные члены очень быстро убывают по величине, а функция Мебиуса делает несколько первых из них отрицательными, включая и по-настоящему большие (при N = 2, N = 3 и N = 5), нелегко представить себе, как же эти главные члены вообще могут внести в разность какой-нибудь иной вклад, кроме как большое отрицательное число. Если в итоге разность должна оказаться положительной (а Литлвуд доказал, что такое рано или поздно случится), то это отрицательное число должно поглотиться большими, положительными, вторичными членами. Чтобы такое произошло, вторичные члены — нули дзета-функции — должны серьезным образом выйти из-под контроля. Судя по всему, так они и делают.
IX.
Чтобы еще глубже разобраться в смысле остаточного члена, снова взглянем на двойную спираль в правой части рисунка . Она представляет нам функцию Li(xкритическая прямая) при x = 20. Критическая прямая — испещренная, если ГР верна, всеми нетривиальными нулями дзета-функции — отображается под действием функции Li(20z) в спираль. Что будет, если вместо 20 мы возьмем какое-нибудь большее значение х? Какой вид примут соответствующие спирали?
Общее представление о том, что при этом происходит, дается на рисунке 21.7. Там представлены три функции: Li(10крит. прямая), Li(100крит. прямая) и Li(1000крит. прямая). Во всех трех случаях показано, как отображается один и тот же отрезок критической прямой — отрезок от 1/2 − 5i до 1/2 + 5i.
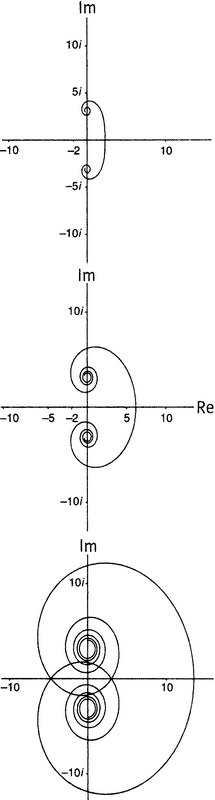
Рисунок 21.7. Li(xкритическая прямая) при x = 10, 100 и 1000. Отображаемая часть критической прямой представляет собой отрезок от 1/2 − 5i до 1/2 + 5i.
Как видно, при увеличении x от 10 до 100 и далее до 1000 происходят следующие явления.
• Спирали растут в размере, но при этом по-прежнему сходятся к тем же двум точкам −πi и πi.
• Отрезок критической прямой, который мы отображаем (длина его равна 10 единицам), все сильнее и сильнее растягивается, накручиваясь все большее и большее число раз вокруг точек −πi и πi.
• Верхняя и нижняя спирали приближаются друг к другу, «целуются» при каком-то значении x между 100 и 1000, а после этого пересекаются (спирали в действительности «целуются», когда x = 399,6202933538…).
Выбранный нами отрезок критической прямой слишком короткий для того, чтобы достичь первой пары нулей при 1/2 ± 14,134725i. Поскольку сама прямая растягивается, а спирали при этом, наматываясь все более и более вокруг точек −πi и πi, растут в размере, возникает интересный вопрос. Не случится ли так, что растяжение прямой и намотка спиралей удержат нули дзета-функции на небольшом удалении от точек −πi и πi независимо от того, сколь сильно увеличились спирали? Ответ — нет; по мере роста x нули дзета-функции отображаются в точки, расположенные сколь угодно далеко. Когда ρ равняется первому нулю дзета-функции (это нуль при 1/2 + 14,134725i), а аргумент x достигает скромного триллиона, функция Li(xρ) добирается до вещественных частей, превышающих 2200.
В главе 14.vii упоминался недавний результат, полученный Бейсом и Хадсоном, — первое литлвудово нарушение (когда π(x) впервые оказывается больше чем Li(x)) происходит до, а весьма вероятно, что и при x = 1,39822×10316. Представим себе, что нам надо повторить весь процесс, с помощью которого мы вычислили π(1000 000), но для указанного числа (назовем его числом Бейса-Хадсона) вместо 1000 000. Какая арифметика была бы тут задействована?
Ясно, что пришлось бы взять не 13, а большее число значений функции J. Корень 1050-й степени из числа Бейса-Хадсона равен 2,0028106…, а корень 1051-й степени равен 1,99896202…, так что надо будет взять корни первой, второй, …, 1050-й степени из этого числа и вычислить функцию J при всех этих аргументах. Это не так уж страшно, потому что многие числа между 1 и 1050 делятся на точные квадраты, а потому функция Мебиуса для них равна нулю. Сколь многие? На самом деле таких чисел 411, так что остается посчитать 639 значений функции J.
Изображенные на рисунке двойные спирали пересекают положительную часть вещественной оси последовательно все далее на восток — в точках 2,3078382, 6,1655995 и 13,4960622. Если бы мы проводили вычисления для числа Бейса-Хадсона, то двойная спираль пересекла бы вещественную ось при гораздо большем значении, определяемом числом, которое начинается как 325 771 513 660 и далее содержит еще 144 цифры до запятой. Спирали при этом невообразимо широкие, но, несмотря на это, все равно сходятся к πi и −πi. Это означает, что верхняя и нижняя спирали в сильной степени накладываются друг на друга — настолько сильно, что на рисунке их невозможно было бы различить. А критическая прямая, испещренная сидящими на ней нулями (если ГР верна!), колоссально растянута. Тогда на рисунке, аналогичном рисунку , в центре была бы значительно большая дыра — хотя все равно с центром в πi, — а спираль триллионы раз наматывалась бы между двумя последовательными нулями с малыми номерами, весьма эффективно разбрасывая их координаты по комплексной плоскости, так что вещественные части колебались бы между чудовищно большими отрицательными и чудовищно большими положительными числами. И все это относится только к первым из 639 строк в таблице для вычисления π(число Бейса-Хадсона). Вторичные члены и правда разошлись не на шутку.
Во всех вычислениях, проводившихся в данной главе, предполагалось (о чем мы время от времени напоминали), что ГР верна. Если она не верна, то наши изящные окружности и спирали представляют собой не более чем приближение, а где-то на большой высоте вдоль критической прямой — для значений ρ где-то далеко-далеко в той бесконечной сумме по вторичным членам — логика нашего рассмотрения рассыпается. В теории, касающейся остаточного члена, ГР занимает центральное место.
X.
Мы достигли главной цели, поставленной перед математической частью этой книги, — показать глубокую связь между распределением простых чисел, воплощенным в функции π(x), и нетривиальными нулями дзета-функции, которые дают значительный (а по теореме Литлвуда — временами и доминантный) вклад в разность между π(x) и Li(x), т.е., другими словами, в остаточный член в ТРПЧ.
Все это открылось нам в блестящей работе Бернхарда Римана 1859 года. Сегодня, конечно, мы знаем намного больше, чем было известно в 1859 году. Однако великая головоломка, впервые сформулированная в той работе, по-прежнему остается нерешенной — она противостоит атакам лучших умов планеты так же твердо, как когда Риман писал о своих «недолгих бесплодных попытках» доказать ее в далекие времена, когда аналитическая теория чисел только-только родилась. Каковы же перспективы на сегодняшний день, когда усилия расколоть орешек ГР прилагаются уже пятнадцатое десятилетие?

