Закон Монтгомери-Одлыжко утверждает, что нетривиальные нули дзета-функции Римана выглядят — имеется в виду статистически — как собственные значения некоторой случайной эрмитовой матрицы. Операторы, представляемые такими матрицами, можно использовать для моделирования определенных динамических систем в квантовой физике. А имеется ли при этом оператор Римана — оператор, собственные значения которого в точности совпадают с нулями дзета-функции? Если да, то какую динамическую систему он представляет? Удастся ли создать такую систему в физической лаборатории? И если удастся, то поможет ли это в доказательстве Гипотезы?

Эти вопросы активно изучались еще до выхода статьи Одлыжко 1987 года. За год до того Майкл Берри опубликовал статью под заглавием «Дзета-функция Римана: Модель квантового хаоса?». Используя ряд хорошо известных и широко обсуждавшихся в то время результатов (и среди них некоторые результаты Одлыжко), Берри обратился к следующему вопросу. Предположим, что риманов оператор существует; тогда динамическую систему какого типа он бы моделировал? Ответ, который он предложил, — хаотическую систему. Чтобы объяснить это, нам надо ненадолго переключиться на знакомство с теорией хаоса.

Тот факт, что чистая теория чисел — наука о натуральных числах и их взаимоотношениях — может соотноситься с субатомной физикой, вовсе не удивителен. В квантовой физике арифметическая составляющая выражена намного сильнее, чем в классической физике, поскольку основополагающая идея состоит в том, что материю и энергию нельзя делить до бесконечности. Энергия передается только в виде 1, 2, 3 или 4 квантов, но никак не 1¹/₂, 2¹⁷/₅₂, √2 или π квантов. Это, конечно, далеко не все, что есть в квантовой механике; ее саму невозможно было бы разработать без наиболее мощных средств самого современного анализа. Например, знаменитое волновое уравнение Шредингера записывается на традиционном языке дифференциального исчисления. Тем не менее арифметическая составляющая в квантовой механике несомненно присутствует, тогда как в классической механике ее практически вовсе нет.

Основания классической физики — физики Ньютона и Эйнштейна — по сути своей аналитические, в математическом смысле. Они опираются на математический анализ, на понятия бесконечной делимости, гладкости и непрерывности, предела и производной, а также вещественных чисел. Не будем забывать, что, именно развивая и доводя понятие «предела» до логического конца, Ньютон и изобрел дифференциальное и интегральное исчисление, в конце концов ставшее содержанием большей части анализа.

Рассмотрим классическую задачу о движении одного тела вокруг другого по эллиптической орбите под действием силы их взаимного гравитационного притяжения. На некотором расстоянии (измеряемом вещественным числом r) от основного тела другое тело (спутник) имеет некоторую строго определенную скорость (выражаемую другим вещественным числом v). Связь между v и r дается точным математическим выражением; v есть в действительности функция от r, выражаемая так называемым уравнением vis viva, знакомым всем, кто изучал элементарную небесную механику:

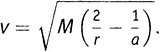
где M и a — некоторые заданные числа, определяемые параметрами системы и начальными условиями — в частности, массами тел и т.п.

На практике, конечно, нельзя достичь бесконечной точности, требуемой для того, чтобы присвоить определенные вещественные значения величинам r и v. Пусть даже мы измеряем r с точностью до 10 или даже 20 знаков после запятой; но ведь для точного выражения вещественного числа требуется бесконечно много десятичных разрядов, а добиться такого мы не можем. Следовательно, для любой реальной орбиты имеется некоторая, пусть очень малая, ошибка при определении вещественных значений буквы r, а также соответствующая ошибка в вычисленных значениях буквы v. Это не играет большой роли: законы Кеплера уверяют нас, что все равно получится правильный эллипс, а математика уравнения vis viva говорит, что ошибка в 1 процент при определении r, как правило, приведет лишь к 0,5-процентной ошибке при вычислении значений v. Таким образом, ситуация управляема и предсказуема. Как говорят математики, «задача интегрируема».

Но это была очень простая задача. Почти все реальные физические проблемы сложнее, чем эта. Рассмотрим, например, случай трех тел, испытывающих взаимное гравитационное притяжение, — знаменитую «задачу трех тел». Можно ли найти ее решение в замкнутом виде, как для уравнения vis viva? Интегрируема ли она?

К концу XIX столетия стало ясно, что ответы таковы: «нет, не можем» и «нет, задача неинтегрируема». Единственный способ получить решение — использовать численные расчеты на компьютере, которые неизбежно носят приближенный характер.

На самом деле в 1890 году Анри Пуанкаре опубликовал статью, внесшую ясность в задачу трех тел: он четко показал, что эта задача не только не допускает решения в замкнутом виде, но и обладает куда более тревожным свойством — ее решения временами приобретают хаотический характер. Это значит, что даже малейшие изменения начальных условий в задаче — аналогов величин M и a в рассмотренном примере задачи двух тел — могут привести к изменению вычисленных орбит до неузнаваемости. Сам Пуанкаре заметил, что один набор условий дает «орбиты столь запутанные, что я даже и не пытался их изобразить».

Согласно распространенному мнению, работа Пуанкаре знаменует собой рождение современной теории хаоса. В течение нескольких десятилетий в теории хаоса не происходило ничего особенного, главным образом потому, что у математиков просто не было средств для обращения с числами — средств для перемалывания чисел в масштабах, требуемых при анализе хаоса. Ситуация изменилась, когда стали доступными компьютеры, и теория хаоса пережила второе рождение в 1960-х годах в трудах метеоролога Эда Лоренца, работавшего в Массачусетсом технологическом институте. Теория хаоса в настоящее время представляет собой обширный предмет, охватывающий много различных более частных дисциплин из физики, чистой математики и вычислительной математики.

Важно осознать, что такая хаотическая система, как решение задачи трех тел, не обязана состоять из случайных движений (и, как правило, из них и не состоит). Прелесть теории хаоса заключается в том, что в хаотических системах присутствуют определенные структуры. В общем случае хаотическая система никогда не проходит снова по раз пройденным положениям, однако она повторяющимся образом воспроизводит указанные структуры; в их основе лежат некоторые правильные, но неустойчивые периодические орбиты, по которым система теоретически могла бы двигаться, если бы нам была доступна бесконечная точность, требуемая для запуска системы именно и абсолютно точно по такой орбите.

При первом появлении современной теории хаоса физики восприняли ее как чисто классический предмет, не имеющий никакого отношения к квантовой теории. Хаос возникает из явлений, подобных тем, какие происходят в задаче трех тел, вследствие того, что начальные условия задаются вещественными числами, числами для измерения, которые можно дробить до бесконечности; их можно изменить на 1 процент, или на 0,1 процента, или на 0,001 процента… Поскольку условия можно варьировать бесконечно, возникает бесконечно много возможных вариантов движения системы. В квантовой же теории, наоборот, начальные условия можно варьировать на 1, 2 или 3 единицы, но не на 1¹/₂ или 2,749. Получается так, что в квантовой теории для хаоса «не должно быть места». Верно, что в квантовой механике имеется некоторая степень неопределенности, но управляющие всем уравнения тем не менее линейны. Малые возмущения приводят к малым последствиям, как это имеет место и для классического уравнения vis viva в задаче двух тел.

И все же в динамических системах квантового масштаба можно наблюдать некоторую степень хаоса. Упорядоченную структуру уровней энергии для электронов на орбите вокруг атомного ядра, например, можно «взболтать», приведя в нерегулярное состояние путем наложения достаточно сильного магнитного поля. (Это, кстати, одна из динамических систем, моделируемых операторами ГУА.) После этого поведение атома становится хаотичным — оно будет радикально другим уже при самом легком изменении начальных условий.

Однако даже если такие системы с квантовым хаосом и сохраняют свое существование в течение некоторого времени, то законы квантовой механики в конце концов приводят их к порядку, отфильтровывая весь хаос. Число разрешенных состояний уменьшается; число запрещенных растет. Чем больше и сложнее система, тем большее время занимает восстановление порядка за счет квантовых законов и тем больше число разрешенных состояний… пока, уже на масштабе нашего обычного мира, утверждение квантового порядка не станет занимать триллионы лет, а число разрешенных состояний не достигнет столь большой величины, что его спокойно можно будет считать бесконечным. Поэтому в классической физике и имеется хаос.

Еще в 1971 году физик Мартин Гутцвиллер нашел способ связать хаотические системы в классическом масштабе с подобными системами в квантовом мире путем взятия предела в уравнениях квантовой механики, когда квантовый множитель — постоянная Планка — стремится к нулю. Таким образом получается «квазиклассическая» система, а периодические орбиты, лежащие в основе классических хаотических систем, отвечают собственным значениям оператора, задающего эту систему.

Майкл Берри показал, что если риманов оператор существует, то он моделирует одну из этих квазиклассических хаотических систем, причем его собственные значения — мнимые части нулей дзета-функции — являются уровнями энергии этой системы. Периодические орбиты в аналогичной классической хаотической системе отвечали бы… — простым числам! (Строго говоря, их логарифмам). Кроме того, он показал, что у этой квазиклассической системы не было бы свойства «симметрии относительно обращения времени» — другими словами, если представить себе, что все скорости всех частиц в системе мгновенно и одновременно заменяются на противоположные, то система не вернется к своему начальному состоянию. (Хаотические системы могут допускать, а могут и не допускать обращение времени. Те, которые его допускают, моделируются не операторами типа операторов ГУА, а операторами другого вида, принадлежащими другому ансамблю — ГОА, т.е. гауссову ортогональному ансамблю.) Работа Берри (в значительной ее части — в сотрудничестве с его коллегой из Бристоля Джонатаном Китингом) представляет собой тонкое и глубокое исследование. Например, он очень детально проанализировал формулу Римана-Зигеля с целью глубоко проникнуть в природу нулей и их влияния друг на друга на различных отрезках их существования. На момент написания книги он пока не отождествил динамическую систему, отвечающую оператору Римана, но если такой оператор существует, то благодаря его работе мы распознаем его немедленно, как только он попадется нам на глаза.

Альтернативный подход развил другой исследователь — Ален Конн, профессор математики из парижского Коллеж де Франс. Вместо того чтобы выискивать, оператор какого типа мог бы иметь своими собственными значениями нули дзета-функции, он просто взял и построил такой оператор.

Это потребовало немалой ловкости. Оператор необходимо снабдить чем-то, на что он может действовать. Операторы того типа, о которых говорилось выше, действуют на пространствах. Плоское двумерное пространство может послужить иллюстрацией общего принципа, если в качестве наглядного пособия взять лист миллиметровки, хотя при этом и придется представлять себе, что он продолжается по всем направлениям до бесконечности. Предположим, что мы повернули это пространство на 30 градусов против часовой стрелки, так что каждая точка в нем тем самым переместилась в некоторую другую точку (за единственным исключением точки, вокруг которой происходит вращение, — она-то остается на месте). Это вращение дает пример оператора. Характеристический многочлен этого конкретного оператора имеет вид x² − √3x + 1, а собственные значения равны ¹/₂√3 + ¹/₂i и ¹/₂√3 − ¹/₂i.

При желании для описания каждой точки в нашем пространстве можно ввести систему координат: для этого надо провести горизонтальную ось x и вертикальную ось y, пересекающиеся в точке вращения, и, как обычно, отложить расстояния в дюймах или сантиметрах вдоль этих осей. Тогда можно заметить, что наш оператор вращения отправляет точку (x, y) в новую точку с другими координатами — которые в действительности равны (¹/₂√3x + ¹/₂y, ¹/₂√3x − ¹/₂y). Для оператора самого по себе это, впрочем, большого значения не имеет — оператор существует и отправляет точки на плоскости в новые точки независимо от какой бы то ни было системы координат. Вращение остается вращением, даже если мы забыли нарисовать пару осей.

Операторы, применяемые в математической физике, разумеется, действуют на значительно более сложных пространствах, чем в нашем примере. Эти пространства не двумерны и даже не трехмерны (подобно обычному пространству, которое окружает нас в быту), и даже не четырехмерны (как пространство-время, возникающее в теории относительности). Они представляют собой абстрактные математические пространства с бесконечным числом измерений. Каждая точка в таком пространстве является функцией. Операторы преобразуют функции в другие функции, а на языке пространств и точек это выражается как отображение одной точки в другую.

Чтобы получить первое представление о том, каким образом функцию можно отождествить с точкой в пространстве, рассмотрим один простой класс функций — квадратичные многочлены p + qx + rx². Семейство всех таких многочленов можно представить в трехмерном пространстве, если многочлену p + qx + rx² поставить в соответствие точку с координатами (p, q, r). В том же духе, четырехмерное пространство будет моделировать кубические многочлены; пятимерное пространство — многочлены четвертой степени и т.п. Далее, поскольку некоторые функции можно записать в виде рядов, а ряд выглядит как бесконечный многочлен (например, e^x записывается в виде 1 + x + ¹/₂x² + ¹/₆x³ + ¹/₂₄х⁴ + …), становится понятно, как бесконечное число измерений может пригодиться при описании функций. На этом языке e^x станет точкой в пространстве, заданной бесконечным набором координат (1, 1, ¹/₂, ¹/₆, ¹/₂₄, …).

Функции, с которыми имеет дело квантовая механика, — это волновые функции, которые определяют вероятность того, что частицы, составляющие описываемую систему, занимают определенные положения и имеют определенные скорости в данный момент времени. Другими словами, каждая точка в пространстве функций представляет некоторое состояние системы. Используемые в квантовой механике операторы кодируют наблюдаемые свойства системы; наибольшую известность имеет оператор Гамильтона, который кодирует энергию системы. Собственные значения оператора Гамильтона представляют собой уровни энергии в системе. Далее, каждое собственное значение определенным образом связывается с вполне определенной точкой (т.е. функцией) в бесконечномерном пространстве, называемой собственной функцией; она служит для представления состояния системы при заданном уровне энергии. Эти собственные функции играют ключевую роль при описании состояний системы. Всякое возможное состояние системы, любое ее физическое проявление дается некоторой линейной комбинацией собственных функций, в точности так же, как всякую точку в трехмерном пространстве можно записать в виде (x, y, z), т.е. в виде линейной комбинации точек (1, 0, 0), (0, 1, 0) и (0, 0, 1).

Ален Конн построил довольно своеобразное пространство, на котором предстояло действовать его риманову оператору. Простые числа встроены в это пространство некоторым способом, заимствованным из понятий алгебраической теории чисел. Дадим краткий обзор работы Конна.

B основе построения всей классической физики лежат вещественные числа, такие как 22,45915771836…; поскольку такие числа не имеют замкнутого вида, требуется бесконечная последовательность десятичных разрядов, чтобы теоретически достичь полной точности. Реальные физические измерения, однако, носят приближенный характер, давая что-то вроде 22,459. Это рациональное число, равное ^22 459/₁₀₀₀. Все, что есть в физическом эксперименте, можно, таким образом, выразить с помощью рациональных чисел — элементов из Q. Чтобы перейти от мира эксперимента к миру теории, надо пополнить поле Q (см. главу 11.v). Другими словами, требуется его расширить таким образом, чтобы для всякой имеющей предел бесконечной последовательности чисел из Q этот предел лежал бы или в самом Q, или в поле-расширении. Обычный и естественный способ такого пополнения приводит к вещественным числам R и комплексным числам С.

Однако в алгебраической теории чисел имеются и другие возможности для пополнения Q. В 1897 году прусский математик Курт Хензель, работая над определенной задачей в теории алгебраических полей, ввел целое новое семейство объектов, подобных полю чисел вида а + b√2, которое мы рассматривали в главе 17.ii. Эти объекты называются p-адическими числами. Для каждого простого числа p имеется по одному из этих экзотических созданий, содержащих бесконечно много элементов. Кирпичики, из которых строится такое поле, — это обсуждавшиеся в главе 17.ii «циферблатные» кольца размера p, p², p³, p⁴ и т.д. В моих обозначениях это кольца CLOCK_p, CLOCK_p2, CLOCK_p3, …. Например, поле 7-адических чисел построено из CLOCK₇, CLOCK₄₉, CLOCK₃₄₃, CLOCK₂₄₀₁, …. Помните приводившуюся ранее иллюстрацию того, как конечное поле можно использовать для построения бесконечного поля? Так вот, здесь используется бесконечное число конечных колец для построения нового бесконечного поля!

Поле p-адических чисел обозначается символом Q_p. Таким образом, имеются поле Q₂, поле Q₃, поле Q₅, поле Q₇, поле Q₁₁ и т.д. Каждое из них — полное поле: Q₂ есть поле 2-адических чисел, Q₃ есть поле 3-адических чисел и т.д.

Как можно догадаться уже из обозначений, p-адические числа чем-то похожи на обычные рациональные числа. Однако поле Q_p богаче и устроено более сложно, чем поле Q, и в некоторых отношениях скорее напоминает поле вещественных чисел R. Как и R, поле Q_p можно использовать для пополнения поля Q.

Здесь вы можете высказать определенное недоумение: «Все отлично, но ведь было сказано, что поле Q_p этих странных новых объектов — р-адических чисел — существует для всякого простого числа p и что любое Q_p позволяет пополнить поле Q; так какое же из них надо предпочесть? Q₂? Q₃? Q₁₁? Q₄₅₈₂₇? Какое простое число должен выбрать профессор Конн, чтобы устроить свой фокус — перекинуть мост между простыми числами и физикой динамических систем?»

Ответ таков: их все! Дело в том, что имеется алгебраическое понятие, называемое аделем, которое охватывает в свои широкие объятия все Q_p для всех простых чисел 2, 3, 5, 7, 11, …. И там же оказываются и вещественные числа! Адели построены из Q₂, Q₃, Q₅, Q_7, … и R способом, напоминающим тот, каким p-адические числа построены из CLOCK_p, CLOCK_p2, CLOCK_p3, …. Если угодно, адели находятся на один уровень абстракции выше p-адических чисел, которые сами располагаются на один уровень абстракции выше, чем рациональные числа.

Если от всего этого у вас кружится голова, то достаточно сказать, что имеется класс суперчисел, являющихся одновременно 2- адическими, 3-адическиими, 5-адическими, … и при этом еще и вещественными. В каждое из этих суперчисел вложены все простые числа.

Без сомнения, адель — довольно заумное понятие. Однако нет на свете ничего настолько заумного, чтобы оно рано или поздно не пробило себе дорогу в физику. В 1990-х годах математические физики взялись за создание адельной квантовой механики, где реальные измерения в эксперименте, приводящие к рациональным числам, воспринимаются как проявление этих причудливых созданий, вытащенных из темных глубин математической бездны.

Пространство такого типа — адельное пространство — и построил Ален Конн в качестве площадки, где может резвиться его риманов оператор. Из-за того что оно адельное, в него, так сказать, встроены все простые числа. Действующие на этом пространстве операторы по необходимости основаны на простых числах. Теперь, я надеюсь, стало немного понятнее, как же можно построить риманов оператор, собственные значения которого являются в точности нетривиальными нулями дзета-функции, а в пространство, на котором он действует, простые числа встроены тем способом, который я пытался описать, но которое при этом имеет отношение к реальным физическим системам — реальным наборам субатомных частиц.

Доказательство Гипотезы Римана (ГР) в этом случае сводится к доказательству определенной следовой формулы — т.е. формулы типа формулы Гутцвиллера, которая связывает собственные значения оператора, действующего на конновском адельном пространстве, с периодическими орбитами в некоторой аналоговой классической системе. Поскольку простые числа уже встроены в одну часть формулы, все должно получиться без труда. Некоторым образом так и происходит, и конструкция Конна элегантна до блеска — уровни энергии в ней суть в точности нули дзета-функции на критической прямой. К сожалению, из нее до сих пор не последовало даже намеков на то, почему же нули дзета-функции не могут оказаться вне критической прямой!

Спектр мнений о ценности построения Конна довольно широк. Вовсе не будучи уверенным, что я сам ее понимаю, я опросил нескольких настоящих математиков, работающих в этой области. Сейчас мне надо продвигаться вперед с крайней осторожностью. Насколько мне известно, Ален Конн, возможно, заявит о доказательстве Гипотезы Римана в тот день, когда эта книга выйдет из печати, и мне не хотелось бы никого вводить в заблуждение. Приведу две цитаты из того, что мне сказали профессионалы:

У меня недостаточно подготовки, чтобы выбрать, какая из точек зрения правильна. Но с учетом высокого положения и способностей математиков X и Y я сильно подозреваю, что одна из них наверняка верна…

Разумеется, активно развиваются и другие подходы к ГР. Алгебраический подход с помощью конечных полей, упомянутый в главе 17, никуда не делся. И, как мы мельком видели в разделе V, этот подход демонстрирует интересные связи с физическим направлением исследований ГР. Аналитическая теория чисел также остается активной областью, способной выдавать сильные результаты.

Имеются два непрямых подхода. Например, есть наша теорема о функции M, получаемой накапливанием значений мебиусовой функции μ. Эта теорема, как было сказано, в точности эквивалентна Гипотезе. Специалист по аналитической теории чисел Деннис Хеджхал из университета Миннесоты использует этот подход, чтобы познакомить с Гипотезой Римана нематематическую аудиторию и при этом избежать введения комплексных чисел. Вот как, по его словам (я пересказываю, а не цитирую), выражается ГР.

Выпишем все натуральные числа, начиная с 2. Под каждым числом запишем его простые делители. Затем, игнорируя всякое число, среди делителей которого есть квадрат (или любая более высокая степень, которая по необходимости содержит в себе и квадрат), будем двигаться вдоль чисел, отмечая как «орел» каждое число с четным числом простых делителей и как «решку» — с нечетным. Получаем бесконечную строку из орлов и решек — нечто вроде того, что возникает в опыте по подбрасыванию монеты:

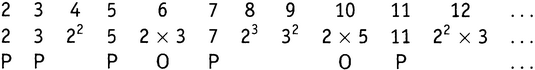
Далее, из классической теории вероятностей хорошо известно, чего ожидать от подбрасывания монеты большое число раз N. В среднем будет ¹/₂N орлов и ¹/₂N решек. Но, разумеется, далеко не всегда будут получаться в точности эти значения. Предположим, мы вычли число орлов из числа решек (или наоборот, в зависимости оттого, какое из них больше). Что мы ожидаем по поводу величины этого избытка? В среднем это будет √N, т.е. N^1/2. Это было известно уже 300 лет назад, во времена Якоба Бернулли. Если подбрасывать «честную» монету миллион раз, то в среднем получится избыток в тысячу орлов (или решек). Может выйти больше или меньше — но в среднем, коль скоро вы продолжаете подбрасывать монету, т.е. при стремлении N к бесконечности, — величина избытка растет в определенном темпе: не быстрее, чем N^1/2+ε для любого сколь угодно малого числа ε. Прямо как у нас в теореме !

На самом деле теорема , которая эквивалентна ГР, утверждает, что функция M растет точно так же, как избыток в опыте по подбрасыванию монеты. По-другому утверждение теоремы можно выразить так: свободное от квадратов число является орлом или решкой — т.е. имеет четное или нечетное число простых делителей — с вероятностью 50:50. Такое положение дел выглядит довольно правдоподобным и может на самом деле оказаться верным. Если вы сможете доказать, что это утверждение действительно верно, то вы тем самым докажете и ГР.

Менее прямой вероятностный подход касается так называемой «модели Крамера». Харальд Крамер (Cramér), несмотря на букву «é» в своей фамилии, был шведом, причем еще одним служащим страховой компании — актуарием в Svenska Livförsöakringsbolaget, но одновременно и талантливым лектором, выступавшим с популярными рассказами о математике и статистике. В 1934 году он опубликовал статью, озаглавленную «О простых числах и вероятности», в которой выдвинул идею, что простые числа распределены настолько случайным образом, насколько это вообще возможно.

Одно из следствий, вытекающее из Теоремы о распределении простых чисел (ТРПЧ), которое было продемонстрировано в главе 3.ix, состоит в том, что в окрестности некоторого большого числа N доля простых чисел составляет ~1/ln N. Например, логарифм триллиона равен 27,6310211…, так что в окрестности триллиона примерно одно из каждых 28 чисел простое. Модель Крамера утверждает, что помимо этого ограничения на среднюю частоту их появления простые числа распределены полностью случайно.

Один из способов понять, что это означает, состоит вот в чем. Представим себе длинный ряд горшков из обожженной глины, на которых написаны натуральные числа: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, … до бесконечности (или до какого-нибудь очень большого числа). В каждый горшок положим некоторое количество деревянных шаров. Число шаров в горшке с номером N должно быть равно ln N (или ближайшему целому числу). Таким образом, первые несколько горшков содержат 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, … этих шаров. Более того, в каждом горшке должен быть по крайней мере один черный шар; все остальные шары в каждом горшке белые. Следовательно, в горшках с написанными на них числами 2, 3 и 4 имеется только черный шар; в горшках с числами от 5 до 12 лежит один черный и один белый; в горшках с 13 по 33 — один черный и два белых и т.д.

Теперь возьмем планшет и большой (желательно бесконечный) лист бумаги и отправимся на прогулку вдоль ряда из горшков. Случайным образом вытащим по шару из каждого горшка. Если это черный шар, запишем номер данного горшка. В конце такой прогулки у нас получится длинный список, начинающийся как 2, 3, 4, …. Шансы, что в списке окажется число 5, распределены как 50:50, поскольку в горшке 5 имеется один белый шар и один черный. Шанс, что там будет число 1 000 000 000 000, — один из 28.

Что же можно сказать о таком списке? Это, конечно, не список простых чисел. Например, в него входит много четных чисел, но лишь одно простое число, 2, является четным. Так вот, если модель Крамера верна, то список будет статистически неотличим от списка простых чисел. Любое общее статистическое свойство, которым обладают простые числа, — скажем, сколь много их мы ожидаем найти в интервале определенной длины или степень их кластеризации (о которой Гильберт в формулировке восьмой проблемы говорил как о «конденсации») — будет присуще и полученному случайному списку.

Чтобы развить некоторую аналогию, рассмотрим десятичные разряды числа π. Насколько вообще известно, их последовательность совершенно случайна. Они никогда не повторяются. И цифры, и пары цифр, и тройки цифр, и четверки цифр появляются с точно такой же частотой, которую даст чистый случай. Никому никогда не удавалось обнаружить какой-нибудь закон в миллиардах десятичных знаков числа π, которые в настоящее время доступны изучению. Десятичные знаки числа π — это случайная последовательность цифр… за тем единственным исключением, что они представляют именно число π! Так же обстоит дело и с простыми числами в модели Крамера. Они неотличимы от любой другой последовательности с частотой появления 1/ln N, и в этом смысле они полностью случайны… за исключением, конечно, того обстоятельства, что они простые!

В 1985 году Хельмут Майер доказал, что модель Крамера в том простом виде, как я ее обрисовал, не дает полной картины распределения простых чисел. Но некоторый модифицированный вариант модели приводит к правильным предсказаниям распределения простых чисел и при этом связан с Гипотезой Римана довольно хитрым и непрямым образом. Имеется скромная надежда, что дальнейшие исследования этого вопроса приведут к прогрессу в понимании ГР.

И наконец, я не могу не упомянуть самый непрямой подход — подход в рамках недедуктивной логики. Строго говоря, это не математическая тема. Математика требует строгих логических доказательств для обоснования своих результатов. Однако большая часть мира устроена иначе. В обычной жизни мы действуем, исходя главным образом из вероятностей. В суде, на приеме у врача, при оформлении страховых полисов мы учитываем именно баланс вероятностей, а вовсе не исходим из железной определенности. Временами, конечно, для количественного выражения подобных вопросов мы пользуемся настоящей математической теорией вероятностей — именно по этой причине страховые компании берут на работу актуариев. Но гораздо чаще мы ее не используем, да и не можем использовать — представим себе хотя бы судебное разбирательство.

Математики порой бросали заинтересованный взгляд на эту сторону жизни. Джордж Пойа даже написал по этому поводу двухтомник, в котором он делает довольно неожиданное заявление, что недедуктивная логика больше ценится в математике, чем в естественных науках. Эту линию рассуждений совсем недавно продолжил австралийский математик Джеймс Фрэнклин. Его статья 1987 года «Недедуктивная логика и математика», опубликованная в British Journal for the Philosophy of Science, содержит раздел, озаглавленный «Свидетельства в пользу Гипотезы Римана и других гипотез».

Фрэнклин подходит к ГР так, как если бы она представляла собой дело, рассматривающееся в суде. Он приводит свидетельства в пользу справедливости Гипотезы Римана.

• Результат Харди 1914 года о том, что на критической прямой лежит бесконечно много нулей.

• Из ГР следует ТРПЧ, о которой известно, что она верна.

• «Вероятностная интерпретация Данжуа» — другими словами, рассмотренное выше рассуждение, основанное на подбрасывании монеты.

• Еще одна теорема 1914 года, которую доказали Ландау и Харальд Бор, согласно которой большинство нулей — все, кроме бесконечно малой доли, — очень близки к критической прямой. Стоит заметить, что коль скоро число нулей бесконечно, один триллион считается бесконечно малой долей.

• Алгебраические результаты Артина, А. Вейля и Делиня, упомянутые в главе 17.iii.

А теперь свидетельства со стороны обвинения.

• У самого Римана не было внятных причин для подкрепления своего утверждения в статье 1859 года о том, что ГР «очень правдоподобна», а полупричины, которые могли бы послужить мотивировкой его утверждения, с тех пор были опровергнуты.

• В 1970-х годах компьютерные расчеты показали, что на большой высоте вдоль критической прямой дзета-функция демонстрирует весьма своеобразное поведение (по-видимому, Фрэнклин не знает о работе Одлыжко).

• Результат Литлвуда 1914 года об остаточном члене Li(x) − π(x). Фрэнклин пишет: «Значимость открытия Литлвуда для Гипотезы Римана далеко не очевидна. Но оно в самом деле дает некоторые основания подозревать, что к Гипотезе Римана могут найтись очень крупные контрпримеры, хотя малые контрпримеры и отсутствуют». Насколько я понимаю, Фрэнклин рассуждает здесь по аналогии. «Для некоторых исключительно больших чисел остаточный член ведет себя плохо. Но он связан с нулями дзета-функции [см. главу 21 в этой книге]. Так что, вероятно, для очень больших T дзета-функция ведет себя плохо и имеет нули вне критической прямой».

Конечно, все это косвенные свидетельства. Однако их не следует сбрасывать со счетов просто как псевдофилософскую игру слов. Выводы, основанные на свидетельствах, могут способствовать получению весьма убедительных результатов, порой вопреки строго аргументированным математическим непреложностям. Рассмотрим, например, очень нематематическую ситуацию, когда гипотезу можно значительно ослабить с помощью подтверждающих ее свидетельств. Гипотеза: ни одно человеческое существо не может быть ростом выше девяти футов. Подтверждающее свидетельство: человек, рост которого 8 футов и 11³/₄ дюйма. Обнаружение такого индивида подтверждает гипотезу… и, однако, в то же время бросает на нее серьезную тень сомнения!