Глава 18. Теория чисел встречается с квантовой механикой

Книга: Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.

Дальше: Глава 19. Поворот Золотого Ключа

I.

В предыдущей главе мы рассмотрели математические предпосылки и некоторые исторические обстоятельства, которые привели к гипотезе Гильберта-Пойа. Эта гипотеза значительно опередила свое время и с полвека пролежала на полке невостребованной.

Эти полвека, однако, оказались очень насыщенными событиями в области физики — вообще самыми насыщенными за всю ее историю. В 1917 году, как раз примерно в то время, когда была выдвинута эта гипотеза, Эрнест Резерфорд открыл делимость атома; 15 лет спустя Кокрофт и Уолтон провели первый в мире эксперимент по искусственному делению атома. Это, в свою очередь, явилось шагом к работам Энрико Ферми и к первой управляемой цепной ядерной реакции, осуществленной в 1942 году, а затем к первому ядерному взрыву 16 июля 1945 года.

«Деление атома», как сообщают своим ученикам все без исключения преподаватели физики в старших классах, — название неправильное. Мы делим атомы всякий раз, как зажигаем спичку. То, о чем идет сейчас речь на самом деле, — это деление атомного ядра, т.е. сердца атома. Чтобы запустить ядерную реакцию — управляемую или уж как получится, — надо выстрелить субатомной частицей в атомные ядра какого-нибудь очень тяжелого элемента. Если сделать это некоторым определенным способом, то ядро расщепится, в свою очередь выстреливая при этом новые субатомные частицы. Эти частицы проникнут в ядра соседних атомов… и т.д., что и приведет к цепной реакции.

А ядра тяжелых элементов — весьма специфические создания. Их можно представлять себе как постоянно бурлящий и колышущийся сгусток из протонов и нейтронов, слипшихся вместе таким образом, что нелегко сказать, где кончается одна частица и где начинается другая. У по-настоящему тяжелых элементов, таких как уран, весь этот сгусток пульсирует на грани неустойчивости. Он может и в самом деле оказаться неустойчивым — это определяется точным соотношением между числом протонов и числом нейтронов — и в этом случае вполне способен разлететься на части по своему собственному усмотрению.

За несколько десятилетий развития ядерной физики в середине XX века возникла потребность хорошо понимать поведение этих странных созданий и, в частности, понимать, что произойдет, если попасть в них другой частицей. Дело в том, что ядро — этот колышущийся сгусток — может существовать в некотором числе состояний, одни из которых обладают большей энергией (здесь надо представлять себе по-настоящему энергичные пульсации), а другие — меньшей (вялые, ленивые пульсации). Если выстрелить частицей в ядро таким образом, чтобы ядро ее поглотило, но само не распалось на куски, то (поскольку энергия частицы не может никуда исчезнуть и поглощается ядром) ядро перейдет из состояния с меньшей энергией в состояние с более высокой энергией. Через некоторое время, утомившись своим пребыванием в возбужденном состоянии, ядро может испустить такую же частицу или, возможно, частицу совсем другого типа и снова оказаться в состоянии с меньшей энергией.

Как много существует энергетических уровней? Когда ядро переходит с уровня a на уровень b? Насколько энергетические уровни отстоят друг от друга и почему именно настолько? Подобная постановка вопроса по сути вводит задачу об исследовании атомного ядра в контекст более широкого круга задач — задач о динамических системах, т.е. о наборах частиц, каждая из которых во всякий момент времени занимает определенное положение в пространстве и имеет определенную скорость. По мере развития исследований в 1950-х годах стало ясно, что некоторые из наиболее интересных динамических систем, включая тяжелые ядра, слишком сложны и не поддаются точному математическому анализу в квантовой области. Число энергетических уровней оказалось слишком большим, а возможные конфигурации слишком многочисленны. Такая картина представляет собой самый устрашающий вариант «задачи многих тел» из классической (т.е. доквантовой) механики, где несколько объектов (например, планеты Солнечной системы) действуют друг на друга посредством гравитации.

Когда приходится иметь дело с таким уровнем сложности, точная математика сталкивается с целым рядом проблем, и поэтому исследования в этой области стали опираться на статистику. Если мы не можем определить, что произойдет точно, то, возможно, нам удастся выяснить, что скорее всего произойдет в среднем. Подобные статистические подходы широко развивались в классической механике начиная примерно с 1850 года, т.е. задолго до появления квантовой теории. В квантовом мире все устроено слегка по-другому, но там, по крайней мере, можно использовать значительный объем результатов, накопленных в классической теории. В конце 1950-х и начале 1960-х годов был создан основной аппарат и были разработаны статистические средства для анализа сложных квантовых динамических систем, подобных ядрам тяжелых элементов. Главными действующими лицами здесь были ядерные физики Юджин Вигнер и Фримен Дайсон. Главным же понятием оказались случайные матрицы.

II.

Случайная матрица — это именно то, что следует из ее названия: матрица, составленная из чисел, выбранных случайным образом. На самом деле не совсем случайным. Позвольте привести пример. Вот случайная (4×4)-матрица достаточно специального типа, важность которого я объясню чуть позже. Для экономии места будем все округлять до четырех знаков после запятой:

Первое, что можно заметить по поводу этой хитроумной штуковины, — данная матрица является эрмитовой: она обладает той самой как бы симметрией относительно главной диагонали, которая упоминалась в главе 17.v. Вспомним еще несколько фактов из той главы.

• С каждой (N×N)-матрицей связан многочлен степени N, называемый характеристическим многочленом.

• Нули характеристического многочлена называются собственными значениями матрицы.

• Сумма собственных значений называется следом матрицы (и равна сумме элементов, занимающих главную диагональ).

• В частном случае эрмитовых матриц все собственные значения вещественны и, следовательно, вещественны и коэффициенты характеристического многочлена, а также след.

Для матрицы из приведенного примера характеристический многочлен имеет вид

x⁴− 1,1836x³− 15,3446x² + 26,0868x − 2,0484,

а собственные значения равны −3,8729, 0,0826, 1,5675 и 4,0864. След равен 1,8636.

Посмотрим теперь повнимательнее на те числа, из которых состоит приведенная выше матрица. Числа, которые мы видим, — вещественные числа на главной диагонали и также вещественные и мнимые части комплексных чисел, занимающих места недиагональных элементов, — случайны в некотором специальном смысле (диагональные случайны с небольшим уточнением, которое будет объяснено ниже). Они выбраны случайным образом из нормального гауссова распределения — знаменитой «колоколообразной кривой», которая повсеместно возникает в статистике.

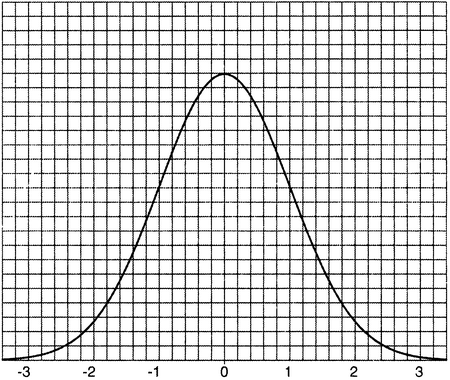
Рисунок 18.1. Нормальное гауссово распределение.

Представим себе стандартную колоколообразную кривую, нарисованную на разлинованном листе бумаги с очень мелкими делениями, так что под кривой расположены сотни квадратиков, образованных разметкой листа (рис. 18.1). Случайным образом выберем один из этих квадратиков; расстояние по горизонтали от него до вертикальной линии, проходящей через середину пика, представляет собой случайное число с нормальным гауссовым распределением. Вблизи самого пика скопилось намного больше этих квадратиков, чем под хвостами кривой, так что с гораздо более высокой вероятностью мы выберем число между +1 и −1, нежели число справа от +2 или слева от −2. Это же видно и из приведенной выше матрицы. (Впрочем, по некоторым техническим причинам элементы на ее главной диагонали в действительности представляют собой случайные гауссовские числа, умноженные на √2, а потому их значения — несколько большие, чем того следовало ожидать.)

Оказалось, что случайные гауссовы эрмитовы матрицы — только гораздо, гораздо большего размера — позволяют моделировать поведение определенных квантовых динамических систем. В частности, их собственные значения, как выяснилось, прекрасно соответствуют энергетическим уровням, которые наблюдаются в экспериментах. По этой причине в 1960-х годах эти собственные значения — собственные значения случайных эрмитовых матриц — стали объектом пристального изучения. В частности, очень интересными оказались интервалы между собственными значениями. Эти интервалы не распределены случайным образом. Например, два уровня оказываются близко друг к другу с гораздо меньшей вероятностью, чем можно было бы ожидать, исходя из случайного распределения. Это явление получило название «отталкивания» — энергетические уровни стараются разойтись по возможности дальше друг от друга, как длинная очередь из малосимпатичных друг другу людей.

Чтобы сделать некое наглядное пособие по этой теме, я попросил математическую программу Mathematica 4, которой я пользуюсь, создать случайную эрмитову матрицу размером 269×269 и вычислить ее собственные значения (рис. ). Причина, по которой выбрано число 269, станет ясной очень скоро. Mathematica, которая не перестает меня удивлять, справилась с задачей в мгновение ока. Все 269 собственных значений попали в интервал от −46,207887 до 46,3253478. Моя идея заключалась в том, чтобы нанизать их, как бусинки, на прямую, тянущуюся от −50 до +50, чтобы они висели там, как дождевые капли на проволочной ограде, а мы, глядя на них, смогли увидеть, имеется ли какой-нибудь порядок в распределении интервалов между ними. Однако это оказалось неосуществимым в пределах книжной страницы, поэтому пришлось порезать прямую на десять отрезков (от −50 до −40, от −40 до −30 и т.д.) и поместить эти отрезки один над другим. В результате получился рисунок 18.2.

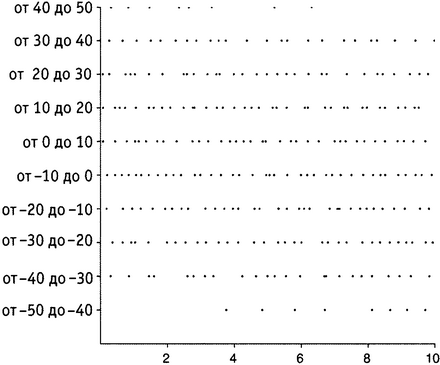
Рисунок 18.2. Собственные значения случайной эрмитовой матрицы размера 269×269.

Никакого явного закона в распределении интервалов не просматривается. Хочется сказать, что они случайны. Но нет! На рисунке показаны 269 чисел, выбранных совершенно случайно в интервале от 0 до 10 и изображенных тем же образом. Сравнение рисунков и позволяет увидеть, что собственные значения случайной матрицы раскиданы по прямой не случайным образом. На рисунке заметен эффект отталкивания, тогда как для случайного разброса на рисунке мы видим, что имеется большее по сравнению с распределением собственных значений число пар, расположенных достаточно близко друг к другу (а потому, неизбежно, и большее количество тех, что сидят дальше друг от друга). Хотя собственные значения на рисунке и отказываются следовать какому-нибудь заметному глазу порядку (в конце концов, они же возникли из случайной матрицы!), они все же изо всех сил стараются сохранять дистанцию между собой. Напротив, чисто случайная точка, судя по всему, совсем не возражает, если ее прижмут к другой случайной точке.

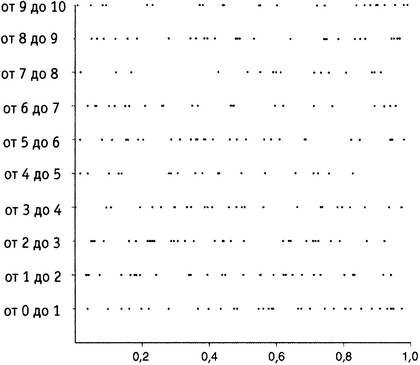
Рисунок 18.3. Случайные интервалы между числами: 269 случайных чисел в интервале от 0 до 10.

Позвольте ввести три профессиональных термина, имеющие прямое отношение к обсуждаемому вопросу. Множество случайных (т.е. гауссовых случайных) эрмитовых матриц описанного типа называется во всей своей совокупности «гауссовым унитарным ансамблем» (ГУА). Точные статистические свойства интервалов в длинных неоднородных строках из чисел типа тех, что фигурируют в приведенных примерах, выражаются так называемой парной корреляционной функцией. А некоторое отношение, связанное с этой функцией и достаточно точно эту функцию характеризующее, называется формфактором.

Теперь я готов рассказать о знаменательной встрече, которая привела к постановке весьма странных и загадочных вопросов о Гипотезе Римана и впоследствии послужила «виновницей» тысяч исследовательских проектов.

III.

Эта встреча произошла в 1972 году, когда в Институте высших исследований в Принстоне случайно столкнулись специалист по теории чисел и физик. Специалистом по теории чисел был Хью Монтгомери — молодой американец, который тогда состоял в аспирантуре в кембриджском Тринити-колледже — колледже Г.X. Харди. Физиком же был Фримен Дайсон, который в то время являлся профессором в принстонском Институте высших исследований. Дайсон, которого мы уже упоминали, был известным физиком. В тот момент он еще не освоил параллельную профессию автора наводящих на размышления бестселлеров о происхождении и будущем человеческого рода.

Как раз незадолго до этого Хью Монтгомери исследовал интервалы между нетривиальными нулями дзета-функции. Это исследование не было частью программы по возможному доказательству Гипотезы Римана. Просто так случилось, что определенный результат о природе этих интервалов имел приложения в области теории чисел, для полей, несколько напоминающих поле а + b√2, с которым мы познакомились в главе 17.ii. Этим и занимался Монтгомери. Вот как звучит эта история в его собственном изложении:

Я сделал эту работу еще будучи аспирантом. Я уже подготовил текст диссертации, но еще не защитился. В начале работы я не понимал, что все это означает. У меня было такое чувство, что здесь нечто скрывается, но я не знал, что именно, и это меня сильно тревожило.

Той весной 1972 года Хэролд Даймонд организовал конференцию по аналитической теории чисел в Сент-Луисе. Я поехал на эту конференцию и сделал там доклад, а потом полетел в Энн-Арбор. К тому моменту я принял приглашение на работу в Энн-Арбор и собирался купить там дом. И действительно купил. Затем, на обратном пути в Англию, я остановился в Принстоне с целью поговорить с Атле [Сельбергом] о своей работе. Я побаивался, что, показав ему свои результаты, услышу в ответ: «Неплохо, Хью, но я доказал все это много лет назад». С моей души упал камень, когда он ничего такого не сказал. Он выказал некоторый интерес, но в целом достаточно поверхностный.

В тот же день вечером мы вместе с Чоула отправились на чай в Фалд-Холл. Посреди комнаты я увидел Фримена Дайсона. Предыдущий год я провел в Институте и прекрасно знал Дайсона в лицо, однако никогда с ним не разговаривал. Чоула спросил: «Вы знакомы с Дайсоном?» Я ответил, что не знаком. Он сказал: «Давайте я вас представлю». Я сказал, что не надо, я как-то не настроен знакомиться с Дайсоном. Но Чоула не отставал и в конце концов поволок меня через всю комнату, чтобы представить Дайсону. Дайсон был очень вежлив и спросил меня, чем я занимаюсь. Я ответил, что изучаю разности между нетривиальными нулями дзета-функции Римана и что у меня есть гипотеза, что в выражении для функции распределения этих разностей под интегралом стоит 1 − (^{sin πu}/_πu)². Он очень оживился и сказал: «Это же формфактор для парных корреляций собственных значений случайных эрмитовых матриц!»

До этого я и не слышал о «парных корреляциях». Оказалось, что именно они являются недостающим связующим звеном. На следующий день Атле передал мне записку Дайсона со ссылкой на книгу Мехты и с указанием на то, какие именно места мне надо посмотреть, и т.д. Этот разговор с Дайсоном остался нашим единственным разговором, и его письмо ко мне также было ровно одно. Но и этого оказалось немало. Я полагаю, что к сегодняшнему дню эту связь все равно удалось бы как-нибудь найти, но, без сомнения, было крупным везением, что она нашлась так быстро, потому что, когда я писал статью в выпускаемый по итогам конференции сборник, я уже был в состоянии использовать соответствующую терминологию, привести ссылки и дать интерпретацию. Забавно, что несколько лет спустя Дайсон опубликовал статью под заглавием «Упущенные возможности». Наверняка имеется масса упущенных возможностей, но моя история представляет собой контрпример. Поистине потрясающее стечение обстоятельств привело к нашей встрече в самый решительный момент.

Нетрудно понять, почему Фримен Дайсон так оживился. Выражение, упомянутое Хью Монтгомери, — выражение, которое возникло из исследований нетривиальных нулей дзета-функции Римана, — оказалось в точности формфактором, связанным с эрмитовыми матрицами, т.е. с объектом, которым Дайсон занимался в течение нескольких лет до этого в ходе исследования квантовых динамических систем. (И Монтгомери даже преуменьшил степень чудесного везения, благодаря которому произошла их встреча. Хотя Дайсон приобрел известность как физик, свою первую ученую степень он получил по математике, причем первой областью его интересов была теория чисел. Если бы не эта его предыстория, то он не смог бы оценить сообщение Монтгомери.)

Чтобы проиллюстрировать сказанное, возьмем все нетривиальные нули дзета-функции Римана до высоты 500i — т.е. на критической прямой от ¹/₂ до ¹/₂ + 500i (на этих небольших высотах мы точно знаем, что Гипотеза Римана верна). В этом интервале имеется 269 нулей (именно поэтому на рисунках и выбрано число 269). Они показаны на рисунке 18.4: интервал, на котором они живут, разбит на 10 отрезков, которые расположены друг над другом аналогично тому, как мы это делали раньше. Сравнивая рисунок 18.4 с рисунками и , можно заметить, что он похож на рисунок , но не на рисунок .

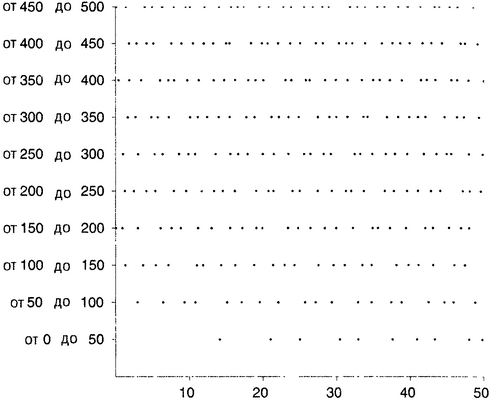
Рисунок 18.4. Первые 269 значений t, где ¹/₂ + ti — нетривиальные нули дзета-функции.

При сравнении этих рисунков надо кое-что принять во внимание. Нулям дзета-функции на рисунке 18.4 требуется некоторое время для «разгона», и в соответствии с принципом, описанным в главе 13.viii, они группируются плотнее в более высоких областях вдоль критической прямой. Кроме того, собственные значения на рисунке расположены несколько более свободно в начале и, соответственно, несколько более тесно в середине. Оба эффекта можно уменьшить, если взять большее количество нулей для большей матрицы, а также использовать нормировку (см. ниже). Даже с учетом этих искажений на основе приведенных рисунков довольно правдоподобными представляются следующие выводы.

• Ни нули дзета-функции, ни собственные значения не похожи на случайным образом разбросанные точки.

• Нули дзета-функции и собственные значения ведут себя похожим образом.

• В частности, и для нулей дзета-функции, и для собственных значений наблюдается эффект отталкивания.

IV.

Статья Монтгомери об интервалах между нулями дзета-функции была опубликована в журнале Американского математического общества в 1973 году. Она начинается словами «На протяжении данной статьи мы принимаем справедливость Гипотезы Римана (ГР)…». В этом нет ничего особенного. К 1973 году множество математических статей состояли из теорем, в которых предполагалась справедливость Гипотезы. На сегодняшний день число их выросло еще больше, и если ГР (как отныне я буду ее именовать, следуя Монтгомери и всем другим современным исследователям) окажется неверной, то вся эта структура обвалится. Правда если контрпримеров окажется немного, значительную часть удастся спасти.

В работе Монтгомери 1973 года содержатся два результата. Первый — это теорема об общих статистических свойствах интервалов между нулями дзета-функции. В этой теореме предполагается справедливость ГР. Второй результат — гипотеза. Она утверждает, что парная корреляционная функция для этих интервалов именно такова, как Монтгомери описал ее в разговоре с Дайсоном. Важно понимать, что это гипотеза. Монтгомери не смог ее доказать даже в предположении о справедливости ГР. И никому другому тоже не удалось этого доказать.

Большая часть свойств нулей дзета-функции Римана, о которых пишут или рассказывают, как и большая часть идей, возникших за последние 30 лет, подобным же образом носят гипотетический характер. В этой области науки наблюдается явный дефицит твердых доказательств. Отчасти это вызвано тем, что после того, как Монтгомери выявил связь между нулями дзета-функции и собственными значениями, исследованиями ГР занялось много физиков и прикладных математиков. Сэр Майкл Берри любит по этому поводу цитировать лауреата Нобелевской премии по физике Ричарда Фейнмана: «Известного куда больше, чем удается доказать». Отчасти же это происходит потому, что ГР представляет собой очень, очень упрямую проблему. ГР посвящено такое грандиозное количество литературы, что приходится все время напоминать себе, что на самом деле о нулях дзета-функции лишь очень мало известно наверняка и даже при всем всплеске интереса в течение нескольких последних лет математически неопровержимые результаты по-прежнему появляются лишь изредка, через длительные интервалы времени.

V.

Институт высших исследований в Принстоне, Нью-Джерси, находится всего в 32 милях от исследовательского центра Белловских лабораторий компании AT&T в Мюррей-Хилл. В 1978 году Хью Монтгомери читал в Принстоне лекции по теме, которая в то время называлась «гипотеза Монтгомери о парных корреляциях». Среди присутствовавших был молодой исследователь Эндрю Одлыжко, работавший в одном из отделов AT&T. Как раз в тот момент они приобрели суперкомпьютер Cray-1. Исследователи с воодушевлением строили планы запуска на нем своих программ и готовились к знакомству с теми алгоритмами, которые отвечали его архитектуре.

Размышляя по поводу лекции Монтгомери, Одлыжко рассуждал следующим образом. Гипотеза Монтгомери утверждает, что интервалы между нулями дзета-функции подчиняются некоторому статистическому закону. Этот закон возникает также при исследовании определенного семейства квантовых динамических систем, которые отвечают модели ГУА. Статистические свойства этого семейства были предметом интенсивного изучения в течение ряда лет. Однако статистические свойства нулей дзета-функции исследовались совсем мало. Пользу могло бы принести восстановление баланса — т.е. исследование статистических свойств нулей дзета-функции.

К этому Эндрю Одлыжко и приступил. Используя в качестве платформы для вычислений свободные процессорные мощности суперкомпьютера Cray в Белловских лабораториях (ограниченные, однако, пятичасовым интервалом для каждого этапа вычислений), он с высокой точностью (около 8 десятичных знаков) получил первые 100 000 нетривиальных нулей дзета-функции Римана, исходя из формулы Римана-Зигеля. Далее, чтобы составить какое-то представление о происходящем много выше по критической прямой, он получил еще 100 000 нулей, начиная с 1000 000 000 001-го. Затем он прогнал эти два множества нулей через разнообразные статистические тесты, чтобы сравнить их с собственными значениями матриц, представляющих ГУА-операторы. Результаты этой работы были опубликованы в 1987 году в знаменитой статье, озаглавленной «О распределении интервалов между нулями дзета-функции».

Результаты оказались не полностью убедительными. Как сам Одлыжко весьма деликатно выразился в своей статье, «все полученные к настоящему моменту данные довольно неплохо согласуются с предсказаниями модели ГУА». Получилось несколько больше малых интервалов, чем это предсказывала модель ГУА. Тем не менее результаты Одлыжко произвели достаточное впечатление, чтобы привлечь внимание исследователей из нескольких различных областей. Дальнейшая работа позволила прояснить ситуацию с несоответствиями, отмеченными в статье 1987 года, и «гипотеза Монтгомери о парных корреляциях» стала законом Монтгомери-Одлыжко.

Закон Монтгомери-Одлыжко

Распределение интервалов между последовательными нетривиальными нулями дзета-функции Римана (в правильной нормировке) статистически тождественно распределению собственных значений ГУА-оператора.

О природе полученных Одлыжко результатов я могу рассказать лишь вкратце. С этой целью я воспроизвел их на своем персональном компьютере, используя список нулей, который Одлыжко любезно разместил на своем веб-сайте. Чтобы избежать всяких аномалий, связанных с малыми значениями, я взял нули от 90 001-го до 100 000-го, если считать вверх по критической прямой от z = ¹/₂. Это составляет 10 000 нулей — вполне достаточно, чтобы извлечь из них некоторый статистический смысл. Нуль с номером 90 001 расположен в точке ¹/₂ + 68 194,3528i, а 100 000-й нуль — в точке ¹/₂ + 74 920,8275i (если округлять до 4 знаков после запятой). Итак, изучим статистические свойства последовательности из 10 000 вещественных чисел, которая начинается числом 68 194,3528, а заканчивается числом 74 920,8275.

Мы говорили в главе 13.viii, что по мере движения вверх по критической прямой нули делаются в среднем ближе друг к другу и поэтому необходимо внести поправку — растянуть верхнюю часть выбранного интервала. Это совсем не сложно сделать, умножив каждое число на его логарифм. У бóльших чисел бóльшие логарифмы, а это как раз и требуется для того, чтобы выровнять среднее расстояние между нулями. В этом и состоит смысл слова «нормировка» в приведенной выше формулировке закона Монтгомери-Одлыжко. Теперь наша последовательность начинается числом 759 011,1279 и заканчивается числом 840 925,3931.

Далее, нас интересуют относительные интервалы между нулями, поэтому можно вычесть 759 011,1279 из каждого числа в последовательности — это не повлияет на результат. Последовательность теперь идет от нуля до числа 81 914,2653. И наконец, просто для того, чтобы сделать числа покрасивее, перейдем к другому масштабу, поделив каждое число на 8,19142653. Это также не повлияет на относительные интервалы, ведь все, что мы сделали, — это сменили масштаб. В этом окончательном виде наша последовательность начинается такими числами: 0, 1,2473, 2,5840 и т.д., а заканчивается числами 9 997,3850, 9 999,1528, 10 000.

Если включить значения на концах, то перед нами будет 10 000 приготовленных для исследования чисел, простирающихся от 0 до 10 000. Поскольку имеется 9999 интервалов между последовательными числами, средний интервал равен 10 000 : 9999, что лишь совсем чуть-чуть больше единицы.

Теперь можно задавать статистические вопросы. Например: как именно интервалы отклоняются от среднего? Сколь многие из них имеют длину меньше единицы? Ответ: 5 349. У скольких из них длина больше 3? Ни у одного. Этот результат радикально отличается оттого, что получается из идеально случайного разброса, где эти числа соответственно равны 6 321 и 489. Это подтверждает те выводы, которые можно извлечь из рисунков и . Наши нули не разбросаны случайным образом. Они более многочисленны вблизи среднего интервала (который слегка превышает 1), и при этом имеется острая недостача интервалов малой или большой величины.

Подсчитав число интервалов величиной от 0 до 0,1, от 0,1 до 0,2 и т.д. и нанеся полученные результаты на гистограмму, масштаб которой выбран так, что полная площадь равна 9999, получаем рисунок 18.5.

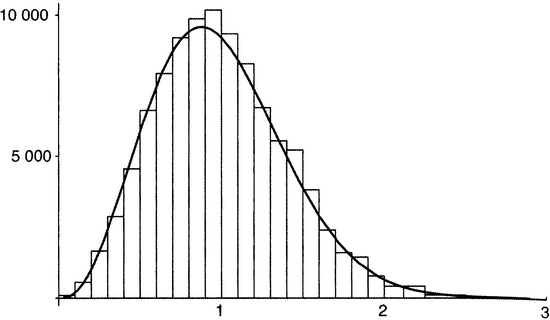
Рисунок 18.5. Закон Монтгомери-Одлыжко (распределение расстояний между нулями дзета-функции от 90 001-го до 100 000-го).

Там показано распределение интервалов между выбранными корнями и для сравнения — кривая, предсказываемая теорией ГУА. Совпадение не слишком хорошее, но и наша выборка не так уж велика или находится недостаточно высоко на критической прямой. Тем не менее соответствие достаточно хорошее, вполне в пределах отклонений, допускаемых случайностью; разумеется, совпадения в статье Одлыжко намного лучше.

VII.

Итак: да, судя по всему, нетривиальные нули дзета-функции и собственные значения случайных эрмитовых матриц некоторым образом связаны друг с другом. Это ставит нас перед довольно серьезным вопросом, который все время висел в воздухе с момента встречи Хью Монтгомери и Фримена Дайсона в Фалд-Холл в 1972 году.

Нетривиальные нули дзета-функции Римана появились при исследовании распределения простых чисел. Собственные значения случайных эрмитовых матриц появились при исследовании поведения систем субатомных частиц, подчиняющихся законам квантовой механики. Скажите, пожалуйста, что вообще может быть общего между простыми числами и поведением субатомных частиц?

Назад: Глава 17. Немного алгебры

Дальше: Глава 19. Поворот Золотого Ключа