Книга: Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.
Назад: Глава 16. Вверх по критической прямой
Дальше: Глава 18. Теория чисел встречается с квантовой механикой
Глава 17. Немного алгебры
I.
Этой книге следовало бы содержать куда больше алгебры, чем в конце концов в ней оказалось. Мы уделяли основное внимание Бернхарду Риману и его работе о простых числах и дзета-функции. Эта работа относится к теории чисел и анализу, и поэтому в нашем рассказе преобладали именно эти темы. Однако современная математика, как уже отмечалось, стала довольно алгебраической. В данной главе читателю предлагаются алгебраические сведения, которые могут потребоваться для понимания двух важных подходов к Гипотезе Римана.
Как и главы 7 и 15, эта глава состоит из двух частей. В разделах II и III обсуждаются основы теории полей, а оставшаяся часть главы посвящена теории операторов. Теория полей важна потому, что она уже позволила доказать нечто, сильно напоминающее Гипотезу Римана. Многие исследователи полагают, что теория полей предлагает наиболее многообещающее направление исследования исходной, классической Гипотезы Римана. Теория операторов приобрела важность после знаменательных и даже романтических событий, о которых будет рассказано в следующей главе. Но сначала о теории полей.
II.
B математике слово «поле» имеет весьма конкретный смысл. Множество элементов образует поле, если эти элементы можно складывать, вычитать, перемножать и делить в согласии с обычными правилами арифметики — например, с правилом a×(b + c) = ab + ac. Результаты всех этих действий должны оставаться в поле.
Например, N не является полем. Если попробовать из 7 вычесть 12, то получится результат, не лежащий в N. Аналогично обстоит дело и с Z — если поделить 12 на 7, то ответ не будет лежать в Z. Это не поля.
Но Q, R и C — поля. Если складывать, вычитать, перемножать или делить друг на друга два рациональных числа, то получится другое рациональное число. То же самое с вещественными и комплексными числами. Они дают нам три примера поля. Ясно, что каждое из этих полей содержит бесконечное число элементов.
Несложно построить и другие бесконечные поля. Рассмотрим семейство всех чисел вида а + b√2, где a и b — рациональные числа. Здесь b или равно нулю, или нет. Если b не равно нулю, то, поскольку число √2 не является рациональным, число а + b√2 также не рациональное. Следовательно, это семейство содержит все рациональные числа (при нулевом b) и тучу весьма специальных иррациональных. Такие числа образуют поле. Сложение числа а + b√2 с числом c + d√2 дает (a + c) + (b + d)√2, их вычитание дает (a − c) + (b − d)√2, результат умножения есть (ac + 2bd) + (ad + bc)√2, а деление с использованием приема, подобного тому, который применяется при делении комплексных чисел, приводит к (ac − 2bd)/(c2 − 2d2) + ((bc − ad)/(c2 − 2d2))√2. Поскольку a и b могут быть вообще любыми рациональными числами, в этом поле бесконечно много элементов.
Поля не обязательно бесконечны. Простейшее из всех полей содержит всего два элемента, 0 и 1. Таблица сложения имеет вид 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 0. Таблица вычитания такова: 0 − 0 = 0, 0 − 1 = 1, 1 − 0 = 1, 1 − 1 = 0. (Можно заметить, что получающиеся результаты таковы же, как для сложения. В данном поле любой знак минус можно спокойно заменить знаком плюс!) Таблица умножения: 0×0 = 0, 0×1 = 0, 1×0 = 0, 1×1 = 1. Таблица деления: 0:1 = 0, 1:1 = 1, а деление на нуль запрещено. (Делить на нуль нельзя никогда.) Это абсолютно нормальное, а вовсе не тривиальное поле, и мы очень скоро не преминем им как следует воспользоваться. Математики называют его полем F2.
На самом деле конечное поле можно построить для любого простого числа р и даже для любой степени любого простого числа. Если p — простое число, то имеется конечное поле из p элементов, поле из p2 элементов, поле из p3 элементов и т.д. Более того, мы только что перечислили все возможные конечные поля. Их можно организовать в список: F2, F4, F8, …, F3, F9, F27, …, F5, F25, F125, …; выписав их все, мы тем самым перечислим все возможности построения конечных полей.
Ошибкой было бы считать (как это порой делают начинающие), что конечные поля представляют собой просто переформулировку арифметики циферблата, описанной в главе 6.viii. Это верно только для полей, содержащих простое число элементов. А вот арифметика других конечных полей устроена более тонко. На рисунке 17.1, например, представлена арифметика циферблата — сложение и умножение — для циферблата с четырьмя отметками (т.е. 0, 1, 2 и 3). Эта система чисел и правил интересна и полезна, но она не является полем, поскольку нельзя разделить 1 ни на 3, ни на 2. (Если бы можно было разделить 1 на 2, то уравнение 1 = 2×x имело бы решение. А у него решения нет.) Математики называют это кольцом, что не лишено основания, коль скоро речь идет о циферблате. В кольце можно складывать, вычитать и умножать, но не всегда можно делить.
| + | 0 | 1 | 2 | 3 | × | 0 | 1 | 2 | 3 | |
| 0 | 0 | 1 | 2 | 3 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 2 | 3 | 0 | 1 | 0 | 1 | 2 | 3 | |
| 2 | 2 | 3 | 0 | 1 | 2 | 0 | 2 | 0 | 2 | |
| 3 | 3 | 0 | 1 | 2 | 3 | 0 | 3 | 2 | 1 |
Рисунок 17.1. Сложение и умножение на циферблате с четырьмя отметками (другими словами, сложение и умножение выполняются по обычным правилам, после чего берутся остатки по модулю 4).
Конкретное кольцо, показанное на рисунке 17.1, имеет официальное обозначение Z/4Z. Должен сознаться, что мне такое обозначение никогда не нравилось, так что на правах автора я изобрету для него свое собственное обозначение: CLOCK4. Ясно, что можно построить такое кольцо для любого натурального числа N. В моих обозначениях оно будет называться CLOCKN.
Но поле FN можно построить не для любого числа N, а только для простых чисел и их степеней. Для простого числа p самого по себе поле Fp выглядит в точности как CLOCKp — та же таблица сложения, та же таблица умножения. Однако для степени простого числа ситуация усложняется. На рисунке 17.2 показаны сложение и умножение (откуда, конечно, извлекаются вычитание и деление) в поле F4. Видно, что F4 отличается от CLOCK4.
| + | 0 | 1 | 2 | 3 | × | 0 | 1 | 2 | 3 | |
| 0 | 0 | 1 | 2 | 3 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 3 | 2 | 1 | 0 | 1 | 2 | 3 | |
| 2 | 2 | 3 | 0 | 1 | 2 | 0 | 2 | 3 | 1 | |
| 3 | 3 | 2 | 1 | 0 | 3 | 0 | 3 | 1 | 2 |
Рисунок 17.2. Сложение и умножение в конечном поле F4.
Всякое поле, конечное или бесконечное, имеет важный параметр — число, называемое характеристикой. Характеристика поля говорит о том, сколько раз надо прибавить единицу к самой себе, чтобы получить нуль. Если 1 + 1 + 1 + … = 0 (где берется N слагаемых), то характеристика равна N. Понятно, что характеристика поля F2 равна 2. Чуть менее очевидно, хотя и без труда проверяется с помощью таблицы сложения на рисунке , то, что характеристика поля F4 тоже равна 2. Такие поля, как Q, R, С, в которых никакое прибавление единицы к самой себе какое угодно количество раз никогда не даст в результате нуль, по определению имеют характеристику «нуль». (Вы могли бы подумать, что более логичной будет характеристика «бесконечность», и вы, возможно, правы, но имеются веские причины и для того, чтобы объявить характеристику нулевой.) Можно проверить, что характеристика любого поля есть или нуль, или некоторое простое число.
Поскольку мы имеем дело с алгеброй, элементы полей не обязаны быть числами. Алгебра позволяет работать с математическими объектами любого типа. Рассмотрим все многочлены (полиномиальные функции) любой заданной степени, т.е. все выражения вида axn + bxn−1 + cxn−2 + …, где a, b, c и т.д. — целые числа. Теперь образуем множество всех рациональных функций, другими словами, функций, являющихся отношением (ratio) двух многочленов. Получим поле. Приведем пример сложения в этом поле:
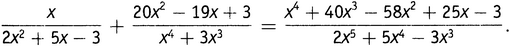
(Примерно этим и занимаются на уроках алгебры в старших классах.)
Коэффициенты многочленов не обязаны быть целыми. На самом деле можно позабавиться, сделав их элементами из конечного поля, такого как рассмотренное выше поле F2. В качестве примера сложения, которое при этом получается, имеем
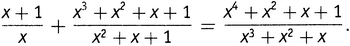
(При проверке этого равенства надо помнить, что в поле F2 выполнено 1 + 1 = 0, а потому x + x = 0, x2 − x2 = 0 и т.д.) Это поле будет называться полем рациональных функций над F2. В нем, разумеется, бесконечно много элементов; лишь коэффициенты ограничены своей принадлежностью к конечному полю. Таким образом, можно использовать конечное поле для построения бесконечного. Заметим еще, что, поскольку 1 + 1 = 0, это поле имеет характеристику 2. Следовательно, и бесконечные поля могут иметь конечную характеристику.
Не имеет особого смысла спрашивать, что собой представляет x в последних двух примерах. Это символ, для манипуляций с которым у нас имеются строго определенные правила. С алгебраической точки зрения главное в этом и состоит. На самом деле почти наверняка ответ на данный вопрос звучит как «x представляет собой число». Однако алгебраисты куда больше интересуются тем, какого типа это число — каким семействам, каким группам, каким полям оно принадлежит и какие правила манипуляций с ним выполнены. Для аналитика же наше число а + b√2 не слишком интересно. «Это просто вещественное число», — скажет аналитик. — «Ладно, алгебраическое число» (см. главу 11.ii), — если на него надавить. Но для алгебраиста, однако, оно представляет особый интерес постольку, поскольку относится к некоторому полю. Вообще алгебраисты и аналитики рассматривают не столько разные вещи, сколько аспекты одной и той же вещи.
III.
Краткий взгляд на размах, мощь и красоту теории алгебраических полей — это все, на что нам здесь хватает места, хотя мы и вернемся ненадолго к полям, рассмотрев их под другим углом зрения в главе 20.v. Я привел здесь этот краткий обзор алгебраических сведений, потому что в 1921 году Артин в своей диссертации, которую он защищал в Лейпцигском университете, применил теорию полей для развития нового подхода к Гипотезе Римана. Соответствующий математический аппарат достаточно серьезен, и я расскажу о нем лишь очень бегло.
Как уже упоминалось в предыдущем разделе, для всякой степени pN простого числа имеется конечное поле. Мы также видели, как конечное поле можно использовать в качестве основы для построения других полей, в том числе бесконечных. Оказывается, что если начать с конечного поля, то имеется способ таким образом построить эти поля-«расширения», что с ними будет связана некоторая дзета-функция. Под «некоторой дзета-функцией» здесь понимается функция комплексного аргумента, определенная над полем комплексных чисел и по целому ряду своих свойств необъяснимым образом напоминающая дзета-функцию Римана. Например, эти аналоги римановой дзета-функции снабжены своим собственным Золотым Ключом — своей собственной эйлеровой формулой произведения, а также своей собственной Гипотезой Римана.
В 1933 году работавшему в Магдебургском университете в Германии Хельмуту Хассе удалось для определенной категории полей доказать результат, аналогичный Гипотезе Римана. В 1942 году Андре Вейль распространил это доказательство на гораздо более широкий класс объектов, а затем предположил — в знаменитых трех «гипотезах Вейля», — что подобные результаты должны иметь место для еще более широкого класса. В 1973 году бельгийский математик Пьер Делинь получил сенсационное достижение, принесшее ему Филдсовскую премию, — он доказал гипотезы Вейля, тем самым, по существу, завершив программу исследований, начало которой положил Артин.
Неизвестно, в какой степени методы, развитые для доказательства аналогов Гипотезы Римана, относящихся к столь замысловатым полям, пригодны для доказательства классической Гипотезы Римана. Но очень многие считают, что вполне пригодны, и данная область остается очень активным направлением в исследовании Гипотезы Римана.
Ведут ли эти исследования куда-нибудь? Это не ясно — по крайней мере, мне не ясно. По поводу существа дела обратимся снова ко второму абзацу в этом разделе, где говорилось, что с полями определенного вида связаны аналоги дзета-функции. Для классической дзета-функции — той, о которой говорится в исходной Гипотезе Римана и которой главным образом и посвящена данная книга, — полем такого вида будет Q, поле обычных рациональных чисел. По мере развития исследований в последние десятилетия выяснилось, что элементарное поле рациональных чисел Q в некотором смысле глубже и более своенравно, нежели «искусственно выведенные» поля, к которым применимы результаты Артина, Вейля и Делиня. Но с другой стороны, методы, развитые для обращения с этими «искусственными» полями, оказались достаточно мощными — Эндрю Уайлс использовал их для доказательства Последней теоремы Ферма!
IV.
Для понимания физической линии в исследовании Гипотезы Римана, генезис которой будет описан в разделе VI и которая открыла исследователям новые обширные территории, следует обратиться к другой алгебраической теме — теории операторов. Поэтому данный раздел, как и следующий, посвящен рассказу об операторах, рассматриваемых с точки зрения связанной с ними теории матриц.
В современной математике и физике матрицы вездесущи, и способность управляться с ними относится к числу основных математических навыков. Из-за ограничений в объеме мне придется спрямить историю, приведя лишь самое необходимое. В частности, я вообще обойду стороной вопрос о вырожденных матрицах, как если бы таких в природе не было. Это, должно быть, самое возмутительное упрощение во всей книге, и я приношу свои извинения математически подкованным читателям.
Матрица — это квадратная таблица из чисел, например 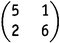 . Целые числа выбраны здесь исключительно для простоты. Числа, входящие в матрицу, могут быть рациональными, вещественными или даже комплексными. Данная конкретная матрица — это матрица 2×2. Матрицы могут быть любого размера, скажем, 3×3, 4×4, 120×120 и т.д. Они могут иметь даже бесконечный размер, хотя для бесконечных матриц правила и подвергаются некоторой модификации. Важная часть во всякой матрице — это ее главная диагональ, т.е. диагональ, ведущая из левого верхнего угла в правый нижний. В нашем примере на главной диагонали стоят элементы 5 и 6.
. Целые числа выбраны здесь исключительно для простоты. Числа, входящие в матрицу, могут быть рациональными, вещественными или даже комплексными. Данная конкретная матрица — это матрица 2×2. Матрицы могут быть любого размера, скажем, 3×3, 4×4, 120×120 и т.д. Они могут иметь даже бесконечный размер, хотя для бесконечных матриц правила и подвергаются некоторой модификации. Важная часть во всякой матрице — это ее главная диагональ, т.е. диагональ, ведущая из левого верхнего угла в правый нижний. В нашем примере на главной диагонали стоят элементы 5 и 6.
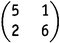 . Целые числа выбраны здесь исключительно для простоты. Числа, входящие в матрицу, могут быть рациональными, вещественными или даже комплексными. Данная конкретная матрица — это матрица 2×2. Матрицы могут быть любого размера, скажем, 3×3, 4×4, 120×120 и т.д. Они могут иметь даже бесконечный размер, хотя для бесконечных матриц правила и подвергаются некоторой модификации. Важная часть во всякой матрице — это ее главная диагональ, т.е. диагональ, ведущая из левого верхнего угла в правый нижний. В нашем примере на главной диагонали стоят элементы 5 и 6.
. Целые числа выбраны здесь исключительно для простоты. Числа, входящие в матрицу, могут быть рациональными, вещественными или даже комплексными. Данная конкретная матрица — это матрица 2×2. Матрицы могут быть любого размера, скажем, 3×3, 4×4, 120×120 и т.д. Они могут иметь даже бесконечный размер, хотя для бесконечных матриц правила и подвергаются некоторой модификации. Важная часть во всякой матрице — это ее главная диагональ, т.е. диагональ, ведущая из левого верхнего угла в правый нижний. В нашем примере на главной диагонали стоят элементы 5 и 6.Если даны две матрицы одного и того же размера, то их можно складывать, вычитать, умножать и делить. Правила, по которым выполняются эти действия, не сразу очевидны. Например, если A и B — две матрицы одного и того же размера, то, вообще говоря, не верно, что А×В = В×А. Правила обращения с матрицами несложно найти в любом обычном учебнике по алгебре, и нам нет нужды вдаваться в них. Достаточно сказать, что такие правила существуют и что имеется арифметика матриц, в целом напоминающая арифметику обычных чисел, только похитрее.
Нам же важно знать про матрицы следующее. Из всякой матрицы (N×N) можно извлечь многочлен N-й степени — полиномиальную функцию, составленную из различных степеней буквы x, вплоть до N-й степени. Боюсь, я не могу объяснить, как же найти этот многочлен для данной матрицы. Придется поверить мне, что он действительно существует и что имеется способ его построить. Этот многочлен называется характеристическим многочленом матрицы.
Характеристический многочлен для приведенной выше матрицы 2×2 равен x2 − 11x + 28. При каких значениях x этот многочлен равен нулю? Это все равно что спросить, каковы решения квадратного уравнения x2 − 11x + 28. По хорошо известной формуле (или, как оптимистически говаривал мой школьный учитель, «путем усмотрения») находим, что решения — это 4 и 7. Ну и правда, если подставить 4 вместо x, то значением многочлена будет 16 − 44 + 28, что в самом деле равно нулю. То же самое и с подстановкой числа 7: 49 − 77 + 28 тоже равно нулю.
Эти факты служат иллюстрацией ситуации, которая верна в общем случае. Всякая (N×N)-матрица имеет характеристический многочлен степени N, и этот многочлен имеет N нулей. Нули характеристического многочлена матрицы невероятно важны. Они называются собственными значениями матрицы. Заметим еще одно. Если сложить числа на главной диагонали нашей (2×2)-матрицы, то получится 11 (поскольку 5 + 6 = 11). Такова же и сумма собственных значений (7 + 4 = 11); и это число противоположно первому из чисел, которые встречаются в характеристическом многочлене (−11 и 11 противоположны). Это очень важное число, называемое следом матрицы.
Характеристический многочлен, собственные значения, след — для чего все это? Видите ли, важность матриц не в них самих, а в том, что они представляют. Матричная арифметика, коль скоро вы ею овладели, — это просто набор технических навыков, как и в обычной арифметике. Но подобно тому, как обычные числа можно использовать для выражения гораздо более глубоких, более фундаментальных вещей, так же используются и матрицы. Прогулка от моего дома до Хантингтон-Вилидж занимает у меня 12 минут; расстояние составляет приблизительно 0,8 мили. Если начиная с завтрашнего утра Соединенные Штаты перейдут на метрическую систему, мне придется говорить «приблизительно 1,3 километра», а не «приблизительно 0,8 мили». Расстояние, однако, от этого не изменится; только числа, используемые для его выражения, пришлось бы изменить. Я по-прежнему проходил бы это расстояние за 12 минут (если только не состоится еще и переход к метрическим единицам времени).
Вот еще один пример: календарь, висящий у меня на стене, представляет собой численное выражение движений Солнца и Луны. Главным образом Солнца, поскольку у нас в Америке принят солнечный календарь, месяцы в котором рассинхронизированы с движением Луны. Однако этот календарь нам дали в соседнем китайском ресторане. Если присмотреться, то можно заметить, что там указаны месяцы и дни традиционного китайского лунного календаря, причем каждый месяц начинается в новолуние. Все числа отличаются от «солнечных» чисел, но они выражают те же небесные явления, то же течение времени, те же фактические моменты времени.
Точно так же обстоит дело и с матрицами. Великое значение матриц в том, что их можно использовать для представления и численного выражения некоторых более глубоких и более фундаментальных вещей. Что же это за вещи? Это операторы. Понятие оператора — одно из самых важных как в математике, так и в физике XX столетия. Я не собираюсь вдаваться в подробности насчет того, что же такое операторы, по крайней мере, до главы 20 точно не собираюсь. Важный момент, который надо осознать, — что это именно они притаились за всей этой суетой с матрицами и что именно их свойства мы и можем численно изучать, используя матрицы.
Теперь понятно, почему характеристический многочлен, собственные значения и след — понятия фундаментальные. Они суть свойства скрывающегося за матрицей оператора, а не матрицы самой по себе. На самом деле данный оператор можно представить многими матрицами, но это обязаны быть матрицы с одними и теми же собственными значениями. Приведенная выше (2×2)-матрица представляет некоторый оператор. Один и тот же оператор представляется и матрицей  и матрицей
и матрицей 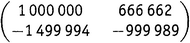 .
.
 и матрицей
и матрицей 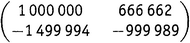 .
.У всех этих матриц — и, конечно, еще у бесконечного числа матриц — один и тот же характеристический многочлен x2 − 11x + 28, одни и те же собственные значения 4 и 7 и один и тот же след 11. Это происходит просто потому, что такими свойствами обладает оператор.
Все это применимо к матрицам любого размера. Возьмем (4×4)-матрицу:

Ее характеристический многочлен равен x4 − 11x3 + 40x2 − 97x + 83. (Можно заметить, что след этой матрицы, как и след приведенной выше, равен 11. Это чистое совпадение, и эти матрицы больше никак не связаны.) Этот многочлен имеет полный набор из четырех нулей. С точностью до пяти знаков после запятой они равны 1,38087, 7,03608, 1,29152 − 2,62195i и 1,29152 + 2,62195i. Это, конечно, собственные значения матрицы. Два из них, как мы видим, являются комплексными числами (причем комплексно сопряженными друг другу, что всегда верно для многочлена с вещественными коэффициентами). Это вполне нормально, даже когда, как в данном случае, все числа в исходной матрице вещественные. Сумма четырех собственных значений равна 11 — мнимые компоненты сокращаются при сложении.
V.
После нескольких десятилетий исследований матриц математики расклассифицировали их на несколько различных типов. Они развили, так сказать, таксономию матриц, в которой полное семейство (N×N)-матриц — называемое математиками общей линейной группой порядка N и обозначаемое как GLN — было разбито на виды и рода.
Выберем всего один из видов в этом большом зверинце — эрмитовы матрицы, названные по имени великого французского математика Шарля Эрмита, с которым мы мельком встречались в главе 10.v. Числа, входящие в эрмитову матрицу, являются комплексными и организованы таким образом, что если число, стоящее в m-й строке и n-м столбце, есть a + bi, то число, стоящее в n-й строке и m-м столбце, есть a − bi. Другими словами, каждый элемент матрицы равен комплексному сопряжению (см. главу 11.v) своего отражения относительно главной диагонали. Попытаюсь прояснить это на примере эрмитовой (4×4)-матрицы:
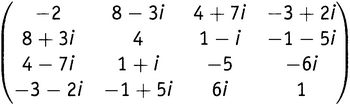
Как видно, элемент в третьей строке и первом столбце равен комплексному сопряжению элемента в первой строке и третьем столбце. Это эрмитова матрица. Заметим, что из определения следует, что все числа на главной диагонали должны быть вещественными, поскольку определение требует, чтобы каждое число на диагонали было комплексно сопряжено самому себе, а этим свойством обладают только вещественные числа: a + bi = a − bi, если и только если b = 0.
Насчет эрмитовых матриц имеется знаменитая теорема, гласящая, что все собственные значения эрмитовой матрицы вещественны. Если немного подумать, то это выглядит несколько неожиданным. Даже когда все элементы какой-либо матрицы вещественны, ее собственные значения могут оказаться комплексными, как мы видели на примере первой из наших (4×4)-матриц. Если же некоторая матрица с комплексными элементами имеет вещественные собственные значения, то это поистине замечательно. Именно так и происходит, если матрица эрмитова. Собственные значения приведенной выше эрмитовой матрицы (приближенно) равны 4,8573, 12,9535, −16,553, −3,2578. Все они вещественны (и в сумме дают −2, т.е. след матрицы).
Из этой теоремы между прочим следует, что все коэффициенты характеристического многочлена эрмитовой матрицы вещественны. Это получается потому, что собственные значения любой матрицы по определению являются нулями характеристического многочлена. Если нули многочлена — это a, b, с, …, то его можно разложить на множители как (x − а)(x − b)(x − c)…. Если здесь просто раскрыть скобки, то получится многочлен в обычном виде. Но раз все числа a, b, с, … вещественные, то раскрытие скобок приводит к выражению, в котором все коэффициенты — вещественные числа. Используя приведенные выше собственные значения нашей эрмитовой (4×4)-матрицы, получаем, что характеристический многочлен равен (x − 4,8573)(x − 12,9535)(x + 16,553)(x + 3,2578). Раскрытие скобок дает характеристический многочлен в виде x4 + 2x3 − 236x2 + 286x + 3393.
VI.
Все это было известно 100 лет назад… Другими словами, в то время, когда Давид Гильберт только приступал к изучению интегральных уравнений, причем исследование операторов играло там ключевую роль. В начале XX века другие математики — одни независимо, другие — вдохновившись работой Гильберта, — также были поглощены исследованием операторов. Операторы просто носились в воздухе. Гипотеза Римана в тот момент тоже висела в воздухе, но не до такой степени, хотя после доклада Гильберта в 1900 году и публикации книги Ландау в 1909-м всерьез задумываться о ней начали многие лучшие умы.
Поэтому не должно показаться слишком неожиданным, что два наиболее блестящих и широко мыслящих интеллекта своего времени смогли соединить эти две вещи. Один из этих интеллектов принадлежал Гильберту, а другой — Джорджу Пойа. И тот и другой, судя по всему, пришли к одному и тому же пониманию независимо друг от друга. Их мыслительные процессы, наверное, развивались примерно таким образом:
Имеется математический объект — эрмитова матрица, которая построена из комплексных чисел, но самая сокровенная и важная характеристика которой — набор собственных значений — неожиданным образом выражается одними лишь вещественными числами. А вот имеется функция — дзета-функция Римана, которая построена из комплексных чисел; и ее наиболее сокровенная и важная характеристика — набор ее нетривиальных нулей. (Для целей данного рассуждения забудем пока о других нулях.) Каждый из этих нулей лежит в критической полосе. Они симметричны относительно критической прямой с вещественной частью 1/2. Скажем, что типичный нуль имеет вид 1/2 + zi с некоторым числом z. Тогда Гипотеза Римана утверждает, что все z — вещественные числа.
Математики 1910-х годов на самом деле сказали бы «оператор», а не «матрица». Хотя матрицы и были разбросаны повсюду после их изобретения Артуром Кэли в 1856 году, они все же не стали всеобщим достоянием, пока около 1925 года на сцене не появилась квантовая механика. И все же здесь можно увидеть грубую аналогию. И набор собственных значений эрмитовой матрицы, и набор нетривиальных нулей дзета-функции представляют собой наборы чисел, возникающих из ключевого свойства существенно комплексных объектов и неожиданным образом оказывающихся вещественными. Отсюда возникает следующая
Гипотеза Гильберта-Пойа
Нетривиальные нули дзета-функции Римана соответствуют собственным значениям некоторого эрмитова оператора.
Происхождение этой гипотезы несколько туманно. И Гильберт, и Пойа должны были бы упоминать возможность некоторой подобной эквивалентности в лекциях или в разговорах в те годы (1910–1920). Но насколько мне удалось установить, ни один из них не воплотил эту мысль в опубликованной статье. Насколько я знаю — и, как сообщает Питер Сарнак, насколько он знает, — единственным письменным свидетельством того факта, что гипотеза Гильберта-Пойа вообще была высказана, остается письмо, которое 20 лет тому назад Пойа написал Эндрю Одлыжко и фрагмент которого приведен на рисунке 17.3. В нем Пойа сообщает, что Эдмунд Ландау задал ему следующий вопрос: «Можете ли вы придумать какую-нибудь физическую причину, в силу которой Гипотеза Римана была бы справедлива?» О том, какие именно предположения делал сам Гильберт, нет вообще никаких известных мне материальных свидетельств.

Рисунок 17.3. Фрагмент письма Джорджа Пойа к Эндрю Одлыжко.
Не следует, однако, забывать, что в математике начала XX века Гильберт был фигурой незаурядного масштаба, а также о том, что он жил и работал в немецкой академической среде, где на университетских профессоров их студенты и подчиненные взирали как на недоступных и всеведущих божеств, приближаться к которым следовало не иначе как с величайшим почтением. Не только к профессору нельзя было и помыслить себе обратиться как-нибудь иначе, нежели «господин профессор», но и жена его становилась «госпожа профессор». Однако для величайших из этих олимпийцев даже такого обращения оказывалось недостаточно. Наиболее выдающимся личностям немецкое правительство присваивало титул Geheimrat, «тайный советник», — примерный эквивалент посвящения в рыцари в Британии. Так что правильное обращение должно было звучать как «господин тайный советник», хотя сам Гильберт и не утруждал себя подобными формальностями.
В силу всего этого неудивительно, что если по удачному стечению обстоятельств вам случалось оказаться в достаточной близости от одного из этих небожителей, чтобы слышать его речь, то вам не скоро удавалось забыть его слова. Конечно, подобные гиганты вызывали к жизни определенное количество не подлежащих проверке апокрифов. И тем не менее, подсчитав все за и против, я склонен думать, что Гильберт в самом деле в какой-то момент высказал гипотезу Гильберта-Пойа или нечто ей эквивалентное. (Между прочим, если бы мы для краткости говорили просто «гипотеза Пойа», это привело бы к недоразумениям, поскольку имеется совершенно другая гипотеза, известная под таким названием.)
Назад: Глава 16. Вверх по критической прямой
Дальше: Глава 18. Теория чисел встречается с квантовой механикой

