Глава 12. Восьмая проблема Гильберта

Книга: Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.

Дальше: Глава 13. Муравей Арг и муравей Знач

I.

Давиду Гильберту было 38 лет, когда утром в среду 8 августа 1900 года он выходил к трибуне 2-го международного конгресса математиков. Сын судьи из столицы Восточной Пруссии Кенигсберга, он прославился как математик за 12 лет до того, решив проблему Гордана в теории алгебраических инвариантов.

То был не просто succès d'estime, но до некоторой степени и succès de scandale. Гильберт смог доказать существование объектов, но при этом не сконструировал их, не предложил даже метода для их построения. Математики говорят о таком как о «доказательстве существования». В своих лекциях Гильберт использовал следующий бытовой пример: «Среди вас имеется по крайней мере один студент — назовем его X, — в отношении которого верно следующее утверждение: ни у одного другого студента в аудитории нет на голове большего числа волос, чем у X. Кто этот студент? Этого мы никогда не узнаем; но в его существовании мы можем быть абсолютно уверены». Доказательства существования довольно распространены в современной математике и в наше время не вызывают особых возражений. Другое дело — Германия 1888 года. Лишь за год до того Леопольд Кронеккер, уважаемый член Берлинской академии наук, выступил с манифестом «О концепции числа», в котором сделал попытку изгнать из математики то, что он считал ненужным уровнем абстракции — все, по его мнению, что нельзя вывести из целых чисел за конечное число шагов. Гордан сам отозвался о гильбертовом доказательстве существования фразой, ставшей знаменитой: «Это не математика. Это теология».

Однако в целом математики признали обоснованность предложенного Гильбертом доказательства. Гильберт вслед за тем продолжил важную работу по алгебраической теории чисел и основаниям геометрии. Он дал новые блестящие доказательства — оба помещающиеся на трех с половиной страницах — трансцендентности чисел π и e. (Когда в 1882 году фон Линдеманн впервые доказал трансцендентность числа π, вышеупомянутый Кронеккер похвалил его за элегантность доказательства, но добавил, что оно ничего не доказывает, ибо трансцендентные числа не существуют!) В 1895 году Гильберт получил место профессора в Геттингене, где и оставался до своего ухода на пенсию в 1930 году.

Слова «Гильберт» и «Геттинген» связаны друг с другом в головах современных математиков столь же тесно, как в других сферах связаны «Джойс» и «Дублин», «Джонсон» и «Лондон». Гильберт и Геттинген играли ведущую роль в математике в течение первой трети XX века — не просто в немецкой математике, а в математике как таковой. Швейцарский физик Пауль Шеррер, студентом приехав в Геттинген в 1913 году, сообщал об обнаружении там «интеллектуальной жизни непревзойденной интенсивности». Необычайно большая доля видных математиков и физиков первой половины столетия училась или в Геттингене, или под руководством кого-то, кто сам там учился.

Относительно личности Гильберта до нас доходят несколько разнородные впечатления. Будучи вполне светским человеком, он был увлеченным танцором и пользовался популярностью как преподаватель. Не чуждался он и погони за юбками — в той весьма ограниченной степени, какая вообще была возможна в провинциальной Германии времен Вильгельма. (Впрочем, нельзя сказать, чтобы эта погоня заводила его достаточно далеко.) В нем была бунтарская жилка: похоже, он тяготился жесткой расписанностью университетской жизни, обычаями, правилами и общественными установлениями. Одна профессорская жена пришла в ужас, узнав, что Гильберта видели в дальней комнате одного из городских ресторанов, играющим в бильярд с младшими преподавателями. Когда во время Первой мировой войны университет отказался предоставить Эмми Нетер постоянную преподавательскую позицию на том основании, что она женщина, Гильберт просто-напросто объявил, что прочитает курс лекций, а затем предоставил Нетер их чтение. Он, по-видимому, был мягким экзаменатором, всегда готовым истолковать сомнение в пользу экзаменуемого.

И все же трудно избавиться от впечатления, что Гильберт был человеком, которому нелегко давалась терпимость к глупцам — категории, к которой он относил весьма значительную часть человечества. Для Гильберта это было тем более печально, что его единственный ребенок, Франц, страдал от серьезного умственного расстройства. Не в состоянии ни изучить как следует какой бы то ни было предмет, ни постоянно работать на одной и той же работе, Франц страдал еще и периодическими приступами паранойи, после которых в течение некоторого времени его приходилось содержать в лечебнице для душевнобольных. Зафиксировано высказывание Гильберта во время первого из этих заточений: «С этого момента мне придется считать, что у меня нет сына».

Как бы то ни было, Гильберт пользовался уважением своих студентов и коллег-математиков. Про него имеется обширное собрание анекдотов, по большей части незлых. Вот только три. Первый касается Гипотезы Римана и взят из англоязычной биографии, написанной Констанс Рид:

У Гильберта был студент, который однажды показал ему работу, претендующую на доказательство Гипотезы Римана. Гильберт тщательно изучил работу; на него произвела большое впечатление глубина аргументации. Но, увы, он обнаружил там ошибку, которую даже он сам не смог устранить. На следующий год студент умер. Гильберт попросил у охваченных горем родителей разрешения выступить с речью на похоронах. Родственники и друзья студента рыдают под дождем возле могилы; Гильберт выходит вперед. Он начинает со слов о том, какая это большая трагедия, что такой одаренный молодой человек умер прежде, чем ему представилась возможность продемонстрировать, чего он в состоянии достичь. Но, продолжает Гильберт, несмотря на то что предложенное этим молодым человеком доказательство Гипотезы Римана содержало ошибку, возможно тем не менее, что однажды доказательство этой знаменитой проблемы будет получено именно на том пути, который наметил покойный. «И в самом деле, — с энтузиазмом продолжал Гильберт, стоя под дождем возле могилы студента, — рассмотрим функцию одной комплексной переменной…»

Второй анекдот я позаимствовал из книги «Универсальный компьютер» Мартина Дэвиса.

Гильберт каждый день появлялся в порванных брюках, что многих смущало. Задачу тактично сообщить Гильберту об этом возложили на его ассистента Рихарда Куранта. Зная о том, какое удовольствие Гильберту приносят длинные прогулки по пересеченной местности, сопровождаемые разговорами о математике, Курант пригласил его пройтись. Устроив при этом так, что им пришлось продираться через заросли колючих кустов, Курант тогда и сказал Гильберту, что тот, похоже, порвал свои брюки об один из таких кустов. «Да нет же, — ответил Гильберт, — они такие уже не одну неделю, хотя никто этого и не замечает».

Третий анекдот апокрифичен, хотя, весьма вероятно, правдив.

Один из студентов Гильберта перестал появляться на занятиях. Поинтересовавшись причиной этого, Гильберт получил ответ, что студент ушел из университета, решив стать поэтом. «Не могу сказать, что я удивлен. Мне всегда казалось, что у него недостаточно воображения, чтобы стать математиком».

Гильберт, между прочим, не был евреем, хотя имя, которым он был наречен, необычное среди немецких христиан, навлекло на него подозрения при Гитлере. Предки Гильберта по отцовской линии относились к фундаменталистской протестантской секте, называемой пиетистами, которые питали пристрастие к Ветхому Завету и к именам-наставлениям. Деда Гильберта звали ни много ни мало Давид Фюрхтеготт Леберехт (т.е. Бойся Бога Живи Праведно) Гильберт.

II.

Констанс Рид так описывает Гильберта во время его выступления на конгрессе 1900 года:

Человеку, который вышел в то утро к трибуне, не было еще сорока; среднего роста и сложения, жилистый, быстрый в движениях, с выступающим высоким лбом, лысый, с отдельными клоками все еще рыжеватых волос. Очки твердо сидели на крупном носу. У него была небольшая борода, растущие в легком беспорядке усы, а под ними рот, неожиданно широко очерченный для столь аккуратного подбородка. Яркие глаза глядели невинно, но твердо из-под сверкающих линз очков.

Гильберт выступил со своим докладом, сделанным по-немецки, в душном актовом зале Сорбонны. Всего на конгрессе было 250 участников, но вряд ли все они присутствовали на выступлении Гильберта утром 8 августа.

Его доклад был озаглавлен «Математические проблемы». Слова, которыми он открывался, стали так же близки математикам XX столетия, как Геттисбергская речь — американским школьникам. «Кто из нас не хотел бы приоткрыть завесу, за которой скрыто наше будущее, чтобы хоть одним взглядом проникнуть в предстоящие успехи нашего знания и тайны его развития в ближайшие столетия?» Гильберт продолжал говорить о том, как важны трудные проблемы, которые концентрируют внимание математиков, способствуя созданию новых направлений развития и новых знаковых систем, и которые также ведут математиков ко все более и более высоким уровням обобщения. Он закончил выступление списком из 23 проблем, «исследование которых может значительно стимулировать дальнейшее развитие науки».

Мне хотелось бы отправиться с вами в обзорное путешествие по 23 проблемам Гильберта. Но тогда эта книга станет недопустимо длинной. А кроме того, имеется обширная, приспособленная к различным уровням понимания литература, с помощью которой такое путешествие осуществимо. Я лишь замечу попутно, что самая первая из проблем Гильберта относилась к упоминавшейся в предыдущей главе континуум-гипотезе, которая посвящена самой сути запутанного вопроса о природе вещественных чисел и возражениям, выдвигавшимся против них Кронеккером. О континуум- гипотезе также имеется обширная литература. Хорошая библиотека или хороший интернет-поисковик вполне удовлетворят любопытство любого, кто захочет обратиться к этой завораживающей задаче.

Только одна из проблем Гильберта — восьмая — имеет прямое отношение к теме нашей книги. Вот она — в переводе Мэри Уинстон Ньюсон из Bulletin of the American Mathematical Society:

8. Проблемы простых чисел

В теории распределения простых чисел в последнее время сделаны существенные сдвиги Адамаром, Валле Пуссеном, Мангольдтом и другими. Для полного решения проблемы, поставленной в исследовании Римана «О числе простых чисел, не превышающих данной величины», необходимо прежде всего доказать справедливость исключительно важного утверждения Римана: все нули функции ζ(s), определяемой рядом

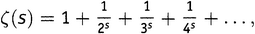
имеют вещественную часть, равную ¹/₂, если не считать известных отрицательных целочисленных нулей. Как только это доказательство будет получено, то дальнейшая задача будет заключаться в том, чтобы использовать бесконечный ряд Римана для более точного определения числа простых чисел и в особенности выяснить, будет ли разность между числом простых чисел, меньших данного числа x, и интегральным логарифмом от x действительно не выше половинного порядка при неограниченно возрастающем x. Далее, действительно ли те члены формулы Римана, которые зависят от первых комплексных нулей функции ζ(s), обусловливают сгущение простых чисел, которое обнаружено при подсчете числа простых чисел.

Тем читателям, которые до сих пор не потеряли нить, этот пассаж должен быть понятен хотя бы отчасти. Я надеюсь, что все целиком приобретет смысл, когда мы доберемся до конца книги. Сейчас главное для нас — тот факт, что Гипотеза Римана рассматривалась как один из 23 больших и сложных вопросов, стоящих перед математиками в XX столетии, и именно так ее рассматривал Давид Гильберт— вероятно, величайший среди математиков, активно работавших в 1900 году.

III.

В главе 10.iii мы кратко упомянули причину, определявшую важность Гипотезы Римана на рубеже столетия. Основным фактором было то, что Теорема о распределении простых чисел была к этому моменту доказана. С 1896 года с математической точностью было известно, что π(N) ~ Li(N), и всеобщее внимание было приковано к этому значку «волны» посередине. Да, по мере того как N неограниченно растет, делаясь все больше и больше, π(N) пропорциональным образом становится все ближе и ближе к Li(N). Но какова природа этой близости? Нельзя ли указать лучшее приближение? И вообще, насколько приближенно это приближение? Каков «остаточный член»?

Когда вопрос с ТРПЧ решился и математики смогли свободно предаваться мыслям об этих «второстепенных» вещах, они обнаружили, что их взор прикован к Гипотезе Римана. В работе Бернхарда Римана 1859 года ТРПЧ не была, конечно, доказана, но та работа явственно подсказывала, что теорема эта верна, и, более того, там предлагалось выражение для остаточного члена. В это выражение входили все нетривиальные нули дзета-функции. Точное знание о том, где, собственно, находятся эти нули, стало делом неотложной важности.

Математическая суть дела будет проясняться по мере нашего продвижения вперед, но, думается, вы вовсе не удивитесь, узнав, что все эти нули — комплексные числа. В 1900 году о расположении этих нетривиальных нулей (имеется в виду расположение на комплексной плоскости) с математической точностью было известно следующее.

• Существует бесконечно много нулей дзета-функции, причем все они имеют вещественную часть, заключенную в пределах от 0 до 1 (не включая границы). Чтобы наглядно это представить, математики используют комплексную плоскость (рис. 12.1) и говорят, что все нетривиальные нули лежат в критической полосе. В Гипотезе Римана делается более сильное утверждение: что все они лежат на линии, вещественная часть которой равна одной второй — т.е. на критической прямой. «Критическая полоса» и «критическая прямая» — распространенные термины при обсуждении Гипотезы Римана, и мы отныне будем свободно ими пользоваться.

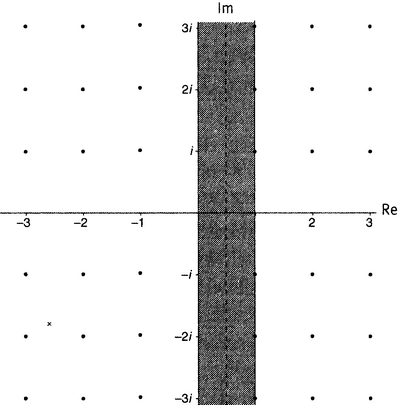
Рисунок 12.1. Критическая полоса (затемнена) и критическая прямая (показана штрихами).

Гипотеза Римана (в геометрической формулировке)

Все нетривиальные нули дзета-функции лежат на критической прямой.

• Нули появляются сопряженными парами. Другими словами, если a + bi — один из нулей, то нулем является и a − bi. Или еще по-другому, если z — один из нулей, то нулем будет и результат его комплексного сопряжения z'. Мы определили «комплексное сопряжение» и обозначения «зет-с-чертой» в главе 11.v. И еще одним способом скажем так: если имеется нуль сверху от вещественной прямой, то его зеркальное отображение снизу от вещественной прямой также будет нулем (верно, разумеется, и обратное).

• Вещественные части нулей симметричны относительно критической прямой, т.е. нуль или имеет вещественную часть, равную ¹/₂ (в духе Гипотезы Римана), или же представляет собой один из элементов пары с вещественными частями ¹/₂ + α и ¹/₂ − α для некоторого вещественного числа α, заключенного между 0 и ¹/₂, и с одинаковыми мнимыми частями. Примерами могли бы служить вещественные части 0,43 и 0,57 или же вещественные части 0,2 и 0,8. Другой способ сказать то же самое таков: если предположить, что имеется нетривиальный нуль не на критической прямой, то его зеркальный образ при отражении относительно критической прямой также должен быть нулем. Это следует из той формулы в главе 9.vi. Если одна сторона формулы равна нулю, то другая также должна равняться нулю. Не будем рассматривать целые значения буквы s (при которых другие члены в той формуле или ведут себя плохо, или обращаются в нуль); тогда эта формула сообщает, что если ζ(s) равна нулю, то ζ(1 − s) также равна нулю. Тем самым, если (¹/₂ + α) + it представляет собой нуль дзета-функции, то нулем является и (¹/₂ − α) − it, а значит, в соответствии с предыдущим пунктом и результат его сопряжения (¹/₂ − α) + it.

Когда Гильберт выступал со своим докладом, сверх этого было известно немного. Риман предложил еще другую формулу с волной для приближенного числа нулей с мнимой частью между нулем и неким большим числом T (см. главу 16.iv). Однако эту формулу доказали лишь в 1905 году (сделал это фон Мангольдт). Но Гипотезу Римана не забыли совсем. Она мелькает как тема для обсуждения в математической литературе 1890-х годов, например, во французском журнале задач L'lntermédiaire des Mathématiciens. Но по сути дела математики XIX века оставили задачу разбираться с великой и ужасной Гипотезой Бернхарда Римана математикам XX столетия.

IV.

XX столетие было довольно… довольно деятельным столетием. Много чего произошло во всех сферах человеческой жизни. Поэтому в ретроспективе век кажется ужасно долгим, намного дольше, чем просто полторы стандартные протяженности человеческой жизни, в общем-то и составляющие век. Но математика выступает величавой неспешной поступью, и глубокие проблемы, исследуемые современными математиками, выдают свои тайны очень медленно и неохотно. Внутри каждой конкретной математической дисциплины мир также довольно тесен, со своими героями, фольклором и устными традициями, связывающими сообщество воедино как в пространстве, так и во времени. Когда я собирал материал для этой книги, то из разговоров с ныне здравствующими математиками сделал вывод, что XX столетие не так уж далеко простерлось во времени — великие имена, связанные с его началом, находятся от нас все еще «в пределах слышимости».

Например, я пишу эти строки всего неделю спустя после разговоров с Хью Монтгомери, ключевым персонажем в достижениях (о которых будет рассказано в подходящий момент) 70-х и 80-х годов XX века. Хью закончил аспирантуру в Тринити-колледже в Кембридже в конце 1960-х. Среди сотрудников колледжа, которых он знал лично, был Джон Идензор Литлвуд (1885-1977), который в 1914 году получил один из первых значительных результатов, продвигающих вперед наше понимание Гипотезы Римана. «Он пытался убедить меня понюхать пороху с этой задачей», — рассказывает Хью, у которого до сих пор сохранились рукописные записки Литлвуда. Литлвуд теоретически мог бы встретиться и говорить о математике с другом Римана Рихардом Дедекиндом, который дожил до 1916 года, продолжая заниматься математикой практически до самого конца жизни, и который учился у Гаусса! (Мне не удалось выяснить, имела ли такая встреча место в действительности. В реальности она не очень вероятна. Дедекинд ушел на пенсию с поста профессора в Брауншвейгской политехнической школе в 1894 году, после чего, согласно Джорджу Пойа, «жил тихой жизнью, встречаясь лишь с очень небольшим числом людей»).

Описываемый период развития математики вызывает сильное ощущение непрерывности, из-за которого меня так и подмывает отбросить строго хронологический подход при рассказе о XX столетии. Это искушение усиливается ввиду характера достижений совершенных в течение этого столетия. История о Гипотезе Римана в XX веке состоит не из одной линии рассказа, а из нескольких нитей, иногда пересекающихся, иногда переплетающихся друг с другом. Здесь требуется маленькое предварительное объяснение; а объяснение само по себе требует предисловия — замечания о том, как математика развивалась в период с 1900 по 2000 год.

V.

Если не считать парижского доклада Гильберта, то 1900 год, конечно, представляет собой произвольную отметку во времени. Математика развивалась равномерно и непрерывно на протяжении всего современного периода. Математики не отправлялись домой с новогодних вечеринок в первые часы 1 января 1900 года (или, если вам больше нравится, 1901 — см. главу 6.ii) с мыслями: «Ага! Уже XX столетие! Нам надо переходить на более высокий уровень абстракции!» — по крайней мере, не в большей степени, чем европейцы, проснувшиеся утром 30 мая 1453 года, думали: «Средние века закончились! Надо бы заняться книгопечатанием, усомниться в авторитете Папы и отправиться открывать Новый Свет!» Мне бы очень не хотелось оказаться в ситуации, когда перед судом моих коллег мне пришлось бы обосновывать термин «математика XX века».

Но при этом все же верно, что математика последних нескольких десятилетий приобрела характерный оттенок, ясно отличающий ее от той математики, которой занимались Гаусс, Дирихле, Риман, Эрмит и Адамар. Насколько его можно передать в одном слове, этот оттенок — алгебраический. Вот начало первого утверждения в книге «Некоммутативная геометрия» Алена Конна, вышедшей в 1990 году и представляющей собой довольно-таки типичный для конца XX века текст по высшей математике:

Классы ограниченных случайных операторов (q_/)_/єx, рассматриваемых по модулю равенства почти всюду, образуют алгебру фон Неймана W(V,F) относительно следующих алгебраических правил…

Алгебраический… алгебра… И это в книге о геометрии! (Кстати, одиннадцатое слово в формулировке последней теоремы — слово и «риманово».)

Происходило же в эти последние десятилетия в общих чертах такое. По ходу большей части своего развития математика твердо опиралась на число. Большая часть математики XIX столетия имела дело с числами: целые числа, рациональные числа, вещественные числа, комплексные числа. В процессе этого развития возникали новые математические объекты, а также раздвигались границы существующих объектов — функций, пространств, матриц — и изобретались новые мощные средства для работы с ними. Но все это так или иначе имело отношение к числам. Функция отображает одно множество чисел в другое множество чисел. Например, функция возведения в квадрат отображает 3, 4 и 5 в 9, 16 и 25; дзета-функция Римана отображает 0, 1 + i и 2 + 2i в −¹/₂, 0,58216 − 0,92685i и 0,86735 − 0,27513i. Аналогично, пространство — это множество точек, задаваемых своими координатами, которые также суть числа. Матрица — это таблица из чисел. И так далее. (Мы будем рассматривать матрицы в главе 17.iv.)

В математике же XX столетия объекты, введенные ранее для выражения важных фактов о числах, сами сделались объектами исследования, и к ним стали применять развитые к тому времени методы изучения чисел и множеств чисел. Математика как бы сорвалась с якоря, привязывающего ее к числу, и воспарила к новым уровням абстракции.

Классический анализ, скажем, имеет своим предметом предел бесконечной последовательности чисел или точек (причем «точка» определяется своими координатами, каковые суть числа). Типичный же продукт XX века — «функциональный анализ», в котором фундаментальный объект исследования — последовательности функций, которые могут сходиться или расходиться и в которых сами функции предлагается рассматривать как «точки» в пространстве бесконечного числа измерений.

Математика уже обратилась сама на себя до такой степени, что даже сами методы исследования и доказательства превратились в объекты изучения. Ряд самых важных теорем в математике XX века касается полноты математических систем (Курт Гедель, 1931) и разрешимости математических пропозиций (Алонсо Черч, 1936).

Но эти основополагающие изменения пока еще, даже в начале XXI века, не нашли своего отражения в математическом образовании (по крайней мере на уровне знаний, необходимых для поступления в университет). Не исключено, что это вообще невозможно. Математика — предмет, где знания накапливаются. Каждое новое открытие что-то добавляет к общему знанию, но ничто никогда оттуда не изымается. Один раз установленная математическая истина навечно остается истиной, и каждое следующее поколение обучающихся должно ее усвоить. Такая истина никогда (ну, практически никогда) не становится неверной или несущественной — хотя и может выйти из моды или же оказаться частным случаем некоторой более общей теории. (Заметьте при этом, что в математике «более общая» не обязательно означает «более сложная». В проективной геометрии имеется теорема Дезарга, которую легче доказать в трех измерениях, чем в двух. Теорема, которую легче доказать в размерности четыре, чем в размерности три, содержится в главе 7 книги Г.С.М. Кокстера «Правильные политопы».)

Молодые и толковые американцы, приступающие к изучению математики в качестве предмета основной специализации на первом курсе в колледже, будут изучать математику, по существу, в том же виде, в каком она была известна молодому Гауссу — возможно, с короткими экскурсами в некоторые области, развитые в более позднее время. Поскольку моя книга нацелена примерно на такой уровень читателей, та математика, о которой здесь рассказывается, в сильной степени пропитана духом XIX века. В повествовательных главах я собираюсь рассмотреть все достижения вплоть до сегодняшнего дня, предлагая для них лучшие объяснения, которые я только смогу придумать, но математические главы этой книги нечасто будут переходить рубеж 1900 года.

VI.

История Гипотезы Римана в XX веке — это история навязчивой идеи, хватку которой рано или поздно почувствовало большинство великих математиков этой эпохи. Примеры одержимости этой идеей имеются в изобилии, как будет видно из нескольких последующих глав. Сначала обратимся к отдельному примеру. Давид Гильберт, как уже рассказывалось, поместил Гипотезу Римана восьмой в списке из 23 проблем, на которых математикам XX столетия предстояло сконцентрировать свои усилия. Это было в 1900 году, до того как навязчивая идея взяла свое. Его умонастроение несколько лет спустя видно из следующей истории, рассказанной его младшим коллегой Джорджем Пойа:

Про германского императора XIII века Фридриха Барбароссу, умершего во время Крестового похода, немцы в массе своей полагали, что он по-прежнему жив, погруженный в сон в пещере глубоко в горах Кифхойзер, готовый к тому, чтобы пробудиться и восстать когда он понадобится Германии. Кто-то спросил Гильберта, что бы он сделал, если бы, подобно Барбароссе, восстал к жизни после сна длиною в несколько столетий. Гильберт ответил: «Я бы спросил, доказал ли кто-нибудь Гипотезу Римана».

А ведь речь идет не о периоде, скудном на мощные проблемы, бросающие вызов ученым. Последняя теорема Ферма (гласящая, что не существует целочисленных решений уравнения xⁿ + yⁿ = zⁿ при n > 2, и доказанная в 1994 году) еще оставалась открытой, как и Проблема четырех красок (о том, что четырех красок достаточно для раскрашивания любой карты на плоскости таким образом, что никакие две соседние области не будут выкрашены одним и тем же цветом, — доказана в 1976 году) и гипотеза Гольдбаха (согласно которой любое четное число, большее двойки, представимо в виде суммы двух простых чисел и которая все еще не доказана), а также множество менее значимых, но давно ждущих своего решения задач, гипотез и головоломок. Гипотеза Римана возвышалась над ними всеми.

Навязчивая идея захватывала различных математиков различными способами, сообразно их математическим наклонностям. Поэтому в течение столетия развивалось несколько направлений — различных подходов к исследованию Гипотезы, у истоков каждого из которых стояла какая-то одна личность, затем передававшая эстафету другим, причем пути этих исследований порой пересекались и перепутывались друг с другом. Например, в рамках вычислительного направления усилия математиков были направлены на явное вычисление все большего и большего количества нулей и на усовершенствованию методов для таких вычислений. Было и алгебраическое направление, инициированное Эмилем Артином в 1921 году в попытке доказать Гипотезу Римана фланговым маневром через раздел алгебры, называемый теорией полей; позднее в том же столетии замечательная встреча двух людей, о которой я расскажу в свое время, привела к возникновению физического направления, соотносящего Гипотезу с математикой, управляющей физикой элементарных частиц. И пока все это продолжалось, специалисты по аналитической теории чисел не прекращали своих усилий, продолжая заложенную самим Риманом традицию по изучению Гипотезы средствами теории функций комплексной переменной.

Исследование простых чисел самих по себе тем временем шло своим чередом, без особенных приложений к Гипотезе, но все же с часто выражаемой надеждой, что новые результаты о распределении простых чисел прольют свет на причину, по которой Гипотеза на самом деле верна — или, если уж так случится, неверна. Ключевыми продвижениями здесь явились развитие в 1930-х годах вероятностной модели для распределения простых чисел и данное в 1949 году Сельбергом «элементарное» доказательство Теоремы о распределении простых чисел, рассмотренной в главе 8.iii.

Рассказывая об этих достижениях, я буду стараться, чтобы в каждый данный момент было ясно, какое из направлений рассматривается, хотя временами ради поддержания общей хронологии рассказа придется перескакивать с одного на другое. Начнем с небольшого вступительного замечания о «вычислительном» направлении, ибо оно проще всего для понимания нематематиками. Каковы в реальности значения — числовые значения — нетривиальных нулей дзета-функции? Как их можно вычислить? И если взять их все вместе, то каковы будут их статистические свойства?

VIII.

Первые конкретные сведения о нулях были получены датским математиком Йоргеном Грамом, вскользь упоминавшимся в главе 10. Будучи математиком-любителем, не работавшим ни в каком университете (а работавшим, подобно поэту Уоллесу Стивенсу, управляющим страховой компанией), Грам, похоже, в течение нескольких лет забавлялся с методами, позволяющими реально вычислять положения нетривиальных нулей (происходило это, понятно, задолго до эры компьютеров). В 1903 году, остановившись на достаточно эффективном методе, он опубликовал список 15 «первых» нулей — тех, которые расположены выше вещественной оси и лежат ближе всего к ней. На рисунке 12.2 грамовские нули показаны жирными точками на критической прямой. Его список, содержавший кое-какие неточности в последних из приведенных знаков после запятой, начинался как

¹/₂ + 14,134725i, ¹/₂ + 21,022040i, ¹/₂ + 25,010856i, ….

Рисунок 12.2. Грамовские нули.

Каждый из выписанных нулей, как видно, имеет вещественную часть, равную одной второй. (А кроме того, существование каждого из корней предполагает и существование сопряженного, расположенного под вещественной осью: ¹/₂ − 14,134725i и т.д. Я буду считать этот факт само собой разумеющимся и не буду упоминать его специально до главы 21, когда он снова станет важным.) Поэтому в тех пределах, докуда они простираются, эти нули подтверждают справедливость Гипотезы Римана. Однако простираются они не слишком далеко. Известным фактом про число нулей — неявно содержавшимся в работе Римана 1859 года — было то, что число их бесконечно. Все ли они имеют вещественную часть, равную одной второй? Риман полагал, что дело так и обстоит — в этом-то и состояла его мощная Гипотеза. Но в тот момент никто не знал, как к этому подступиться.

После появления списка Грама математики, должно быть, взирали на него со священным ужасом. Тайна распределения простых чисел, которая удерживала на себе внимание математиков со времен легендарного Гаусса, оказалась каким-то образом заключенной в перечне чисел: ¹/₂ + 14,134725i, ¹/₂ + 21,022040i, ¹/₂ + 25,010856i, …. Но как?! Их вещественные части, без сомнения, равняются одной второй, как и предполагал Риман; однако мнимые части не проявляют никакого очевидного порядка или системы.

Я только что сказал: «Математики, должно быть…» Мне надо было бы сказать: «Несколько математиков в континентальной Европе, должно быть…» Одержимость Гипотезой Римана, захватившая математиков в течение XX столетия, в 1905 году только набирала силу. Во многих частях света о ней толком и не знали. В следующей исторической части нашего повествования мы с читателем отправимся в Англию, в период эдвардианского расцвета ее имперской славы. Но сначала позвольте показать вам, как же на самом деле выглядит дзета-функция.

Назад: Глава 11. Обитатели матрешек

Дальше: Глава 13. Муравей Арг и муравей Знач