Книга: Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.
Назад: Глава 8. Не лишено некоторого интереса
Дальше: Глава 10. Доказательство и поворотная точка
Глава 9. Расширение области определения
I.
Итак, мы начинаем приближаться к Гипотезе Римана. Просто чтобы освежить память, сформулируем ее еще раз:
Гипотеза Римана
Все нетривиальные нули дзета-функции имеют вещественную часть, равную одной второй.
И мы уже знаем, что такое дзета-функция! Если s — некоторое число, большее единицы, то дзета-функция определяется таким выражением (9.1):
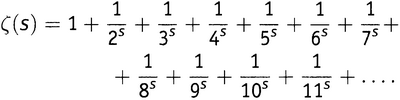
или же, несколько более изысканным образом,
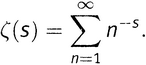
где слагаемые бесконечного ряда отвечают всем положительным целым числам. Мы видели, что если к этой сумме применить процедуру, напоминающую решето Эратосфена, то ее можно переписать как
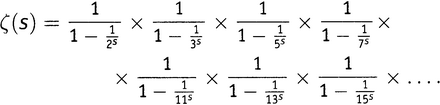
то есть

где множители в бесконечном произведении отвечают всем простым числам.
Таким образом, получаем
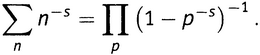
что я и назвал Золотым Ключом.
Пока все прекрасно, но что это там говорилось насчет нетривиальных нулей? Что такое нуль функции? Что представляют собой нули дзета-функции? И когда они нетривиальны? Не переживайте, сейчас все будет!
II.
Позабудем на время о дзета-функции. Рассмотрим бесконечную сумму совсем другого типа:
S(x) = 1 + x + x2 + x3 + x4 + x5 + x6 + ….
Сходится ли она вообще когда-нибудь? Без сомнения. Если x равно 1/2,то сумма представляет собой просто-напросто выражение из главы 1.iv, поскольку (1/2)2 = 1/4, (1/2)3 = 1/8 и т.д. Следовательно, S(1/2) = 2, потому что именно к этому значению ряд и сходится. Более того, если вспомнить правило знаков, то (−1/2)2 = 1/4, (−1/2)3 = −1/8 и т.д., а следовательно, S(−1/2) = 2/3 согласно выражению из главы 1.v. Аналогичным образом выражение говорит нам, что S(1/3) = 11/2 выражение — что S(−1/3) = 13/4. Легко получить и еще одно значение для этой функции: S(0) = 1, поскольку нуль в квадрате, кубе и т.д. все равно равен нулю, и остается только единица, с которой ряд начинается.
Однако если x равен 1, то S(1) есть 1 + 1 + 1 + 1 + …, а этот ряд расходится. При x равном 2 расходимость еще более явная: 1 + 2 + 4 + 8 + 16 + …. Когда x равен −1, происходит странная вещь: по правилу знаков сумма принимает вид 1 − 1 + 1 − 1 + 1 − 1 + …. Такая сумма равна нулю, если взять четное число членов, и единице, если нечетное. Данное выражение определенно не убегает на бесконечность, но оно и не сходится. Математики рассматривают такое поведение как некоторый вид расходимости. Ситуация с x = −2 еще хуже: сумма 1 − 2 + 4 − 8 + 16 − … ведет себя так, словно убегает на бесконечность сразу по двум направлениям. Такая ситуация определенно далека от сходимости, и если вы скажете, что здесь налицо расходимость, то никто с вами спорить не будет.
Короче говоря, функция S(x) имеет значения, только когда x лежит в границах между −1 и 1, не включая сами границы. В других случаях у нее значений нет. В таблице 9.1 приведены значения функции S(x) для аргументов x между −1 и 1.
| −1 или меньше | (нет значений) |
| −0,5 | 0,6666… |
| −0,333… | 0,75 |
| 0 | 1 |
| 0,333… | 1,5 |
| 0,5 | 2 |
| 1 или больше | (нет значений) |
Таблица 9.1. Значения функции S(x) = 1 + x + x2 + x3 + ….
Вот и все, что можно извлечь из бесконечной суммы. График этой функции показан на рисунке 9.1; на этом графике у функции нет вообще никаких значений к западу от −1 и к востоку от 1. Используя профессиональную терминологию, можно сказать, что область определения этой функции заключена строго между −1 и 1.
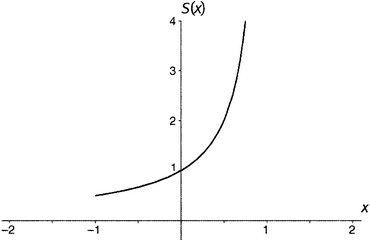
Рисунок 9.1. Функция S(x) = 1 + x + x2 + x3 + ….
III.
Но смотрите, нашу сумму
S(x) = 1 + x + x2 + x3 + x4 + x5 + …
можно переписать в таком виде:
S(x) = 1 + x(1 + x + x2 + x3 + x4 + …).
Ряд в скобках здесь равен просто S(x): каждый член, встречающийся в одном, встречается также и в другом из двух выписанных выше рядов, а это и означает, что они совпадают.
Другими словами, S(x) = 1 + xS(x). Перенося самый правый член в левую часть, получаем равенство S(x) − xS(x) = 1, или, другими словами, (1 − x)S(x) = 1. Следовательно, S(x) = 1/(1 − x). Возможно ли, чтобы за нашей бесконечной суммой скрывалась столь простая функция, как 1/(1 − x)? Может ли равенство
1/(1 − x) = 1 + x + x2 + x3 + x4 + x5 + x6 + … (9.2)
оказаться верным?
Без сомнения, может. Если, например, x = 1/2, то 1/(1 − x) равняется 1/(1 − 1/2), что есть 2. Если x = 0, то 1/(1 − x) равно 1/(1 − 0), что есть 1. Если x = −1/2, то 1/(1 − x) равняется 1/(1 − (−1/2)), т.е. 1:11/2 что есть 2/3. Если x = 1/3, то 1/(1 − x) равняется 1/(1 − 1/3) т.е. 1:2/3, что есть 11/2. Если x = −1/3, то 1/(1 − x) равняется 1/(1 − (−1/3)), т.е. 1:11/3, что есть 3/4. Все сходится. Для аргументов −1/2, −1/3, 0, 1/3, 1/2, при которых мы знаем значения функции, значения бесконечного ряда S(x) такие же, как и значения функции 1/(1 − x). Похоже, что этот ряд и эта функция — одно и то же.
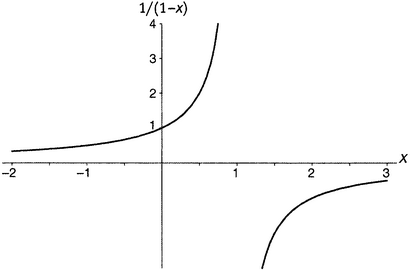
Рисунок 9.2. Функция 1/(1 − x).
Но они не одно и то же, поскольку у них различные области определения, как это видно из рисунков и . S(x) имеет значения только между −1 и 1, не включая границы; функция же 1/(1 − x) имеет значения везде, за исключением точки x = 1. Если x = 2, то ее значение равно 1/(1 − 2), то есть −1. Если x = 10, то значение равно 1/(1 − 10), то есть −1/9. Если x = −2, то значение равно 1/(1 − (−2)), то есть 1/3. Можно нарисовать график функции 1/(1 − x). Как видно, он совпадает с предыдущим графиком в промежутке между −1 и 1, но имеет еще и значения к западу от −1 (включая саму −1) и к востоку от 1.
Мораль здесь в том, что бесконечный ряд может определять только часть функции; или, используя подобающие математические термины, бесконечный ряд может определять функцию только на части ее области определения. Остальная часть функции может где-то прятаться, ожидая, пока ее не вытащат на свет с помощью фокуса типа того, что мы применили к S(x).
IV.
Это приводит к очевидному вопросу: а не обстоит ли дело подобным же образом и с дзета-функцией? Не случилось ли так, что бесконечная сумма, которую мы использовали для дзета-функции, — выражение — описывает только часть этой функции? И у этой функции есть что-то еще, что нам только предстоит открыть? Может ли область определения дзета-функции
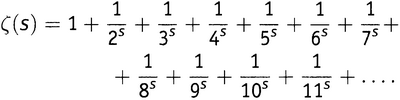
оказаться больше, чем просто «все числа, большие 1»?
Конечно может. Иначе зачем бы мы тут стали влезать во все эти подробности? Да, дзета-функция имеет значения при аргументах, меньших 1. На самом деле, как и функция 1/(1 − x), она имеет значения при всех числах за единственным исключением x = 1.
Сейчас подходящий момент, чтобы привести график дзета-функции, который продемонстрировал бы все ее свойства в широком интервале значений. К сожалению, это невозможно. Как уже упоминалось, кроме как для простейших функций, обычно нет хорошего и надежного способа показать функцию во всем ее великолепии. Близкое знакомство с функцией требует времени, терпения и тщательного изучения. Можно, однако, изобразить дзета-функцию по кускам. На рисунках с 9.3 по 9.10 показаны значения ζ(s) для некоторых аргументов, находящихся слева от s = 1, хотя для этого потребовалось выбрать свой собственный масштаб на каждом графике. Понять, где мы находимся, можно, руководствуясь подписанными аргументами (на горизонтальной оси) и значениями (на вертикальной оси). При обозначении масштаба m указывает на миллион, tr на триллион, mtr обозначает миллион триллионов, a btr — миллиард триллионов.
Коротко говоря, когда s лишь немного меньше единицы (рисунок ), значения функции очень большие по величине и отрицательные — как если бы при движении на запад при пересечении линии s = 1 значения внезапно переметнулись из бесконечности в минус бесконечность. Если продолжить путешествие по рисунку — т.е. устремлять s ближе и ближе к нулю, — то подъем вверх радикально замедляется. Когда s равно нулю, ζ(s) равна −1/2. При s = −2 кривая пересекает ось s, т.е. ζ(s) равна нулю.
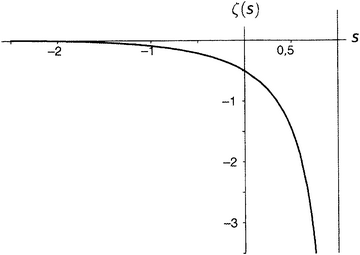
Рисунок 9.3.
Затем (мы по-прежнему двигаемся на запад, добравшись теперь до рисунка 9.4) график взбирается на относительно скромную высоту (в действительности до 0,009159890…), а после этого поворачивает вниз и снова пересекает ось при s = −4. График попадает в неглубокую впадину (−0,003986441…), а после нее снова взбирается вверх и пересекает ось при s = −6. Еще один невысокий пик (0,004194…), спуск до пересечения с осью при s = −8 и далее в несколько более глубокую впадину (−0,007850880…), затем пересечение с осью в точке −10, после чего уже довольно заметный пик (0,022730748…), пересечение с осью при s = −12, впадина поглубже (−0,093717308…), пересечение с осью при s = −14 и т.д.
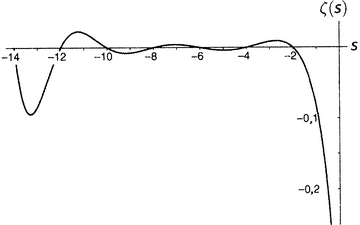
Рисунок 9.4.
Дзета-функция равна нулю при каждом отрицательном четном числе, а по мере продвижения на восток (рисунки от 9.5 до 9.10) последовательные пики и впадины быстро делаются все более и более значительными. Последняя показанная впадина расположена при s = −49.587622654…, а глубина ее составляет около 305 507 128 402 512 980 000 000. Сами видите, как нелегко изобразить дзета-функцию на одном графике.
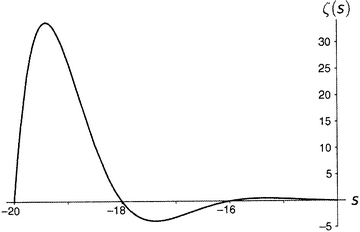
Рисунок 9.5.
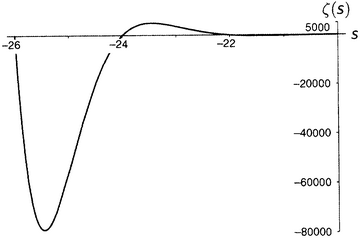
Рисунок 9.6.
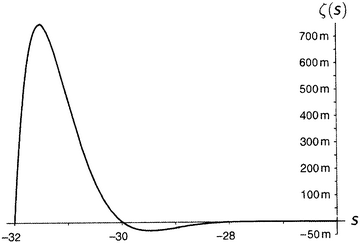
Рисунок 9.7.
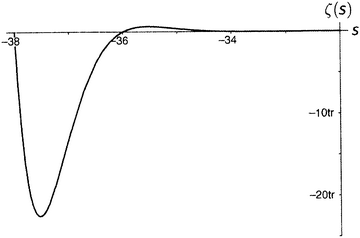
Рисунок 9.8.
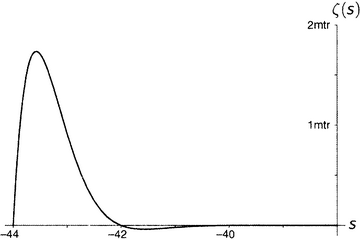
Рисунок 9.9.
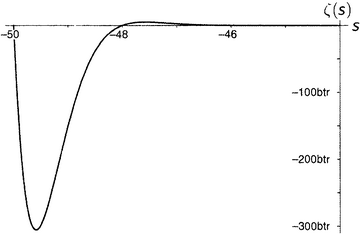
Рисунок 9.10.
V.
Ho как я получил все эти значения ζ(s) для s, меньших 1? Мы уже видели, что бесконечный ряд из выражения для этого непригоден. А что пригодно? Если бы ради спасения своей жизни мне пришлось вычислить значение ζ(−7,5), как бы я к этому подступился?
Я не могу объяснить этого в полной мере, потому что такое объяснение требует слишком значительного погружения в математический анализ. Но я попробую передать общую идею. Сначала определим некоторую новую функцию, используя бесконечный ряд, слегка отличный от ряда в выражении . Это η-функция; η (читается «эта») — седьмая буква греческого алфавита. Определим η-функцию как
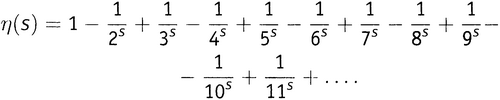
Грубая прикидка подсказывает, что у этой функции перспективы сходимости лучше, чем у выражения . Вместо непрестанного прибавления чисел здесь мы по очереди то прибавляем, то вычитаем, так что каждое следующее число до некоторой степени сокращает вклад предыдущего. Так оно и выходит. Математики в состоянии доказать — хотя здесь мы этим заниматься не будем, — что этот новый бесконечный ряд сходится всегда, когда s больше нуля. Это существенное улучшение по сравнению с выражением , которое сходится, только когда s больше единицы.
Но какая нам от всего этого польза в отношении дзета-функции? Для начала заметим, что в силу элементарных алгебраических правил A − B + C − D + E − F + G − H + … равно (A + B + C + D + E + F + G + H + …) минус 2×(B + D + F + H + …). Поэтому функцию η(s) можно переписать как
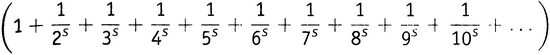
минус
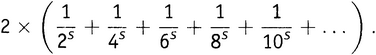
Первая скобка — это, конечно, ζ(s). Вторую скобку легко упростить, пользуясь 7-м правилом действий со степенями: (ab)n = anbn. Таким же образом каждое из этих четных чисел можно разбить в произведение вида 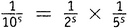 , после чего можно вынести
, после чего можно вынести 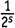 в качестве множителя перед всей скобкой. А что останется в скобке? Там останется ζ(s)! Коротко говоря,
в качестве множителя перед всей скобкой. А что останется в скобке? Там останется ζ(s)! Коротко говоря,
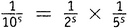 , после чего можно вынести
, после чего можно вынести 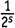 в качестве множителя перед всей скобкой. А что останется в скобке? Там останется ζ(s)! Коротко говоря,
в качестве множителя перед всей скобкой. А что останется в скобке? Там останется ζ(s)! Коротко говоря,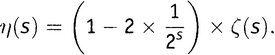
или, переписав это «наоборот» и слегка причесав, получаем
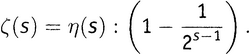
Вот. Это означает, что если нам удастся узнать какое-то значение η(s), то мы немедленно будем знать и значение ζ(s). А поскольку можно узнать значения η(s) между 0 и 1, можно получить и значение ζ(s) в этом промежутке, несмотря на то что «официальный» ряд для ζ(s) там не сходится.
Пусть, например, s равно 1/2. Если сложить 100 членов ряда для η(1/2), то получится 0,555023639…; если сложить 10 000 членов, получится 0,599898768…. В действительности значение η(1/2) составляет 0,604898643421630370…. (Существуют определенные приемы позволяющие вычислять такое без необходимости сложения мириад членов.) Вооруженные всем этим, мы можем вычислить значение ζ(1/2) оно оказывается равным −1,460354508…, что выглядит очень правдоподобно, если судить по первому графику из приведенного выше набора.
Но задержимся на мгновение. Не устроили ли мы тут игру в наперстки с двумя бесконечными рядами, один из которых сходится при аргументе s = 1/2, а другой — нет? Ну, строго говоря, мы действуем не совсем по правилам, и я обошелся довольно безответственно с той математикой, на которой здесь все основано. Однако же я получил правильный ответ, причем этот фокус можно повторить для любого числа между нулем и единицей (не включая ее) и получить правильное значение для ζ(s).
VI.
За исключением одного только s = 1, где ζ(s) не имеет значения, мы можем теперь предъявить значение дзета-функции для любого числа s, большего нуля. А как насчет аргументов равных нулю или меньших нуля? Вот здесь все по-настоящему круто. Один из результатов в работе Римана 1859 года состоит в доказательстве формулы, впервые предложенной Эйлером в 1749 году, которая выражает ζ(1 − s) через ζ(s). Таким образом, если мы желаем узнать, например, значение ζ(−15), то надо просто вычислить значение ζ(16) и подставить его в эту формулу. Это, правда, неслабая формула, и я привожу ее главным образом для полноты картин:
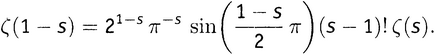
Всюду здесь π — это магическое число 3,14159265…, sin — добрая старая тригонометрическая функция синус (от аргумента, выраженного в радианах), а знак «!» обозначает факториальную функцию, упоминавшуюся уже в главе 8.iii. В математике, изучаемой в старших классах, вы встречались только с факториальной функцией, аргументами которой являются положительные целые числа: 2! = 1×2, 3! = 1×2×3, 4! = 1×2×3×4 и т.д. В высшей математике, однако, есть способ определить факториальную функцию для всех чисел, кроме отрицательных целых, для чего применяется прием расширения области определения вполне в духе того, которым мы только что пользовались. Например, (1/2)! оказывается равным 0,8862269254… (на самом деле — половине квадратного корня из π), (−1/4)! = 1,2254167024… и т.д. Отрицательные целые создают проблемы в этой формуле, но это не критические проблемы, и я ничего о них говорить не буду. На рисунке 9.11 изображена полная факториальная функция для аргументов от −4 до 4.
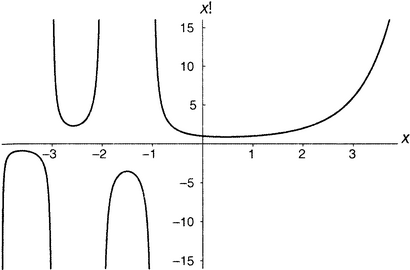
Рисунок 9.11. Полная факториальная функция x!.
Если вам кажется, что все это немного чересчур, то просто примите на веру, что имеется способ получить значение функции ζ(s) для любого числа s за единственным исключением s = 1. Даже если ваш взгляд никак не сфокусируется на приведенной выше формуле, то заметьте по крайней мере вот что: она выражает ζ(1 − s) через ζ(s); если вы знаете, как посчитать ζ(16), то вы можете тогда вычислить ζ(−15); если вам известна ζ(4), то вы можете вычислить ζ(−3); если вам известна ζ(1,2), то вы можете выделить ζ(−0,2); если вам известна ζ(0,6), то вы можете вычислить ζ(0,4); если вам известна ζ(0,50001), то вы можете вычислить ζ(0,49999), и т.д. Вопрос, к которому я подбираюсь, — это что аргумент «одна вторая» имеет особый статус в приведенном соотношении между ζ(1 − s) и ζ(s), потому что если s = 1/2, то 1 − s = s. Очевидно — я хочу сказать, очевидно из рисунка и рисунков с по 9.10, — что дзета-функция не симметрична относительно аргумента 1/2. И тем не менее ее значения при аргументах слева от 1/2 связаны с их зеркальными образами справа весьма тесным, хотя и не самым простым образом.
Снова посмотрев на набор графиков, можно заметить кое-что еще: ζ(s) равна нулю всегда, когда s — отрицательное четное число. А если при каком-то аргументе значение функции равно нулю, то этот аргумент называется нулем данной функции. Итак, верно следующее:
−2, −4, −6 и все остальные отрицательные четные целые числа являются нулями дзета-функции.
А взглянув на утверждение Гипотезы Римана, мы увидим, что в ней говорится про «все нетривиальные нули дзета-функции». Неужели мы у цели? Увы, нет: отрицательные четные числа и в самом деле нули дзета-функции, но все они до единого — тривиальные нули. Чтобы добраться до нетривиальных нулей, нам надо нырнуть поглубже.
VII.
В качестве добавления к этой главе еще чуть разовьем наш анализ, применив к выражению два результата из тех, что были сформулированы в главе 7. Выпишем это выражение снова:
1/(1 − x) = 1 + x + x2 + x3 + x4 + x5 + x6 + …
Все, что я собираюсь сделать, — это проинтегрировать обе части. Поскольку интеграл от 1/x равен ln x, я надеюсь, что не слишком злоупотреблю вашим доверием, если скажу (не останавливаясь на доказательстве), что интеграл от 1/(1 − x) равен −ln(1 − x). С правой частью равенства все еще проще. Можно просто интегрировать один член за другим, используя правила интегрирования степеней, сформулированные в таблице . Результат (впервые полученный сэром Исааком Ньютоном) имеет вид:
−ln(1 − x) = x + x2/2 + x3/3 + x4/4 + x5/5 + x6/6 + ….
Будет чуть удобнее, если обе части умножить на −1:
ln(1 − x) = −x − x2/2 − x3/3 − x4/4 − x5/5 − x6/6 − … (9.3)
Несколько странно, хотя для наших целей и несущественно, что выражение верно при x = −1, тогда как выражение , с которого мы начали, при этом неверно. Действительно, при x = −1 выражение дает следующий результат:
ln 2 = 1 − 1/2 + 1/3 − 1/4 + 1/5 − 1/6 + 1/7 − … (9.4)
Отметим сходство с гармоническим рядом. Гармонический ряд… простые числа… дзета-функция…. Во всей этой области господствует логарифмическая функция.
Правая часть выражения несколько своеобразна, хотя этого и не заметить невооруженным взглядом. Она в действительности является стандартной (из учебников) иллюстрацией того, насколько хитрой вещью являются бесконечные ряды. Этот ряд сходится к ln 2, что составляет 0,6931471805599453…, но только если складывать члены именно в этом порядке. Если складывать в другом порядке, ряд может сойтись к чему-нибудь другому — или может даже вообще не сойтись!
Рассмотрим, например, такую перестановку членов ряда: 1 − 1/2 − 1/4 + 1/3 − 1/6 − 1/8 + 1/5 − 1/10 − …. То же самое, но с расставленными скобками: (1 − 1/2) − 1/4 + (1/3 − 1/6) − 1/8 + (1/5 − 1/10) − …, т.е. 1/2(1 − 1/2 + 1/3 − 1/4 + 1/5 − …). Сумма ряда с переставленными членами равна половине сумм исходного ряда!
Ряд из выражения — не единственный, обладающий таким настораживающим свойством. Сходящиеся ряды разбиваются на две категории: те, у которых есть такое свойство, и те, у которых его нет. Ряды, подобные рассмотренному, сумма которых зависит от порядка суммирования, называются «условно сходящимися». Ряды, ведущие себя получше и сходящиеся к одному и тому же пределу независимо от того, как переставлены слагаемые, называются «абсолютно сходящимися». Большая часть важных в анализе рядов сходятся абсолютно. Тем не менее для нас первоочередной интерес будет представлять еще один ряд, сходящийся лишь условно, подобно ряду из выражения . Мы встретимся с ним в главе 21.

