Найденное пифагорейцами доказательство иррациональности квадратного корня из двух опирается на аргумент, называемый rеductio ad absurdum — приведение к абсурду: мы принимаем за истину некоторое утверждение, выводим следствия из него, наталкиваемся на противоречие и тем самым устанавливаем ложность посылки. В качестве современного примера рассмотрим афоризм великого физика ХХ столетия Нильса Бора: «Противоположность любой глубокой идеи является другой глубокой идеей». Если это утверждение истинно, у него могут найтись довольно опасные следствия. Представьте, например, отрицание золотого правила, заповеди, запрещающей лгать, или заповеди «Не убий». Поэтому давайте разберемся, является ли сам афоризм Бора глубокой идеей. Если это так, то противоположный ему тезис: «Противоположность любой глубокой идеи не является другой глубокой идеей» — тоже должен быть истинным. Тем самым мы достигли reductio ad absurdum. Поскольку обратное утверждение ложно, данный афоризм не должен нас сковывать, ибо в соответствии с ним же самим он не является глубокой идеей.

Мы приведем современную версию доказательства иррациональности квадратного корня из двух, опирающуюся на reductio ad absurdum и простые алгебраические выкладки, а не чисто геометрическое доказательство, открытое пифагорейцами. Стиль доказательства и способ размышления не менее интересны, чем получаемый результат.

Рассмотрим квадрат со стороной, равной единице (одному сантиметру, одному дюйму, одному световому году — не суть важно).

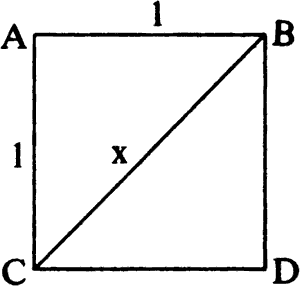
Диагональ ВС делит квадрат на два прямоугольных треугольника. В таких прямоугольных треугольниках, согласно теореме Пифагора, 1² + 1² = х². Поскольку 1² +1² = 1 + 1 = 2, то х² = 2, и мы можем записать, что х = √2, то есть корню квадратному из двух. Предположим, что √2 является рациональным числом, то есть √2 = p/q, где p и q — целые числа. Они могут быть любыми, сколь угодно большими, но обязательно целыми числами. Мы, конечно, потребуем, чтобы у них не было общих делителей. Если мы, например, заявляем, что √2 = 14/10, то, безусловно, можем сократить эту дробь на множитель 2 и записать: p = 7, q = 5 вместо p = 14, q = 10. Будем далее считать, что у числителя и знаменателя сокращены все общие множители. Для выбора значений p и q y нас остается бесконечное число вариантов. Возведя в квадрат равенство √2 = p/q, получим: 2 = р²/q², или после домножения обеих частей на q²:

p² = 2q² (1)

Таким образом, р² представляет собой некоторое число, умноженное на 2. Однако квадрат любого нечетного числа является нечетным числом (1² = 1,3² = 9,5² = 25,7² = 49 и т. д.). Получается, что само число ρ должно быть четным, то есть можно записать ρ = 2s, где s — некоторое целое число. Подставив его в уравнение (1), находим:

p² = (2s)² = 4s² = 2q².

Деление обеих частей последнего равенства на 2 дает: g 2 = 2s 2. То есть q 2 тоже является целым числом, и, опираясь на тот же аргумент, что был использован для р, мы заключаем, что q тоже является четным. Но если числа p и q оба делятся на два, значит, они содержат несокращенный общий делитель, что противоречит нашему предположению. Reductio ad absurdum. Но в чем состояло предположение? Доказательство не может запретить нам сократить общие множители, разрешив использовать 14/10, но запретив 7/5. Поэтому ошибочным должно быть начальное предположение: p и q не могут быть целыми числами, a √2 является иррациональным числом. В действительности √2 = 1,4142135…

Насколько ошеломляющее и неожиданное заключение! Какое элегантное доказательство! Но пифагорейцы считали необходимым скрывать это великое открытие.