Модель оценки капитальных активов (capm)

Нобелевские лауреаты в области экономики за 1990 г. Гарри Марковиц и Уильям Шарп разработали теории финансовых рынков, которые оказали сильное влияние на инвесторов. Работа Гарри Марковица ныне известна как современная портфельная теория. Задумавшись о составе активов, которые инвесторы должны включать в свои портфели, Марковиц обнаружил, что основные свойства актива, которые должны принимать во внимание инвесторы, – это риск и доходность. Выбирая для своего портфеля различные инструменты, инвесторы могут определить и контролировать общий риск портфеля с помощью вариационного анализа каждого из них. Говоря простым языком, инвесторы могут сформировать портфели рискованных акций, при этом общий риск портфеля будет ниже, чем риск любой отдельной акции в портфеле. Определив данную степень риска, инвесторы формируют портфель, который обеспечит самую высокую ожидаемую доходность.

Эту концепцию можно проиллюстрировать на простом примере. Предположим, вы имеете портфель, средства в котором равномерно распределены между акциями двух компаний: сектора компьютерных технологий и пищевого сектора. При благоприятной экономической ситуации, когда объем продаж компьютеров растет, цена акций технологической компании, как ожидается, вырастет более чем на 50 %, акции продовольственной компании принесут ожидаемую доходность в размере 6 % (включая дивиденды). В период экономического спада, когда продажа компьютеров идет очень вяло, ожидается, что цена акций технологических компаний упадет на 20 %. При этом акции продовольственной компании, относящейся к оборонной промышленности (и обеспечивающей стратегическую продовольственную безопасность), вырастут на 40 %. Таким образом, при благоприятной экономической ситуации инвесторы получат среднюю доходность в размере 28 % [(50 % + 6 %) / 2]. В период рецессии средняя доходность портфеля составит 10 % [(40 % – 20 %) / 2].

Несмотря на то что акции компаний технологического сектора являются более рискованными по сравнению с акциями компаний пищевого сектора, средняя доходность за счет диверсификации инвестиций будет выше, чем если бы все средства были инвестированы в 1 ценную бумагу. Помимо снижения риска за счет увеличения количества акций можно снизить риск, выбрав акции, которые по-разному реагируют на экономическую ситуацию.

Впоследствии Уильям Шарп и Джон Линтнер развили идею Марковица, разработав модель оценки капитальных активов – CAPM. Модель оценки капитальных активов определяет соотношение между риском и ожидаемой доходностью акции. Ожидаемая доходность акции – это ставка безрисковых инвестиций с учетом премии за риск, при этом за основу берется системный риск акции. В этой модели риск акции или портфеля делится на две составляющие: системную и несистемную. Риск, присущий ценной бумаге (например, деловой или финансовый риск), можно снизить и устранить путем диверсификации. Остается системный риск, который обретает значение в связи с риском и доходностью. Иными словами, комбинируя в портфеле различные акции, можно понизить несистемный, или диверсифицируемый, риск, а оставшийся риск – это системный риск. Системный, или рыночный, риск – это отношение стоимости ценной бумаги к изменениям цен на рынке в целом. Некоторые акции могут расти или падать в цене быстрее рынка, а другие отличаются меньшей волатильностью, чем рынок. Системный риск обозначается греческой буквой бета. Коэффициент бета (β), мера системного риска акции, определяет чувствительность доходности акции к доходности рынка и определяется следующим образом:

Коэффициент бета = (Стандартное отклонение доходности акции / Стандартное отклонение доходности рынка) ×

× Коэффициент корреляции между доходностью акции и рынка.

Чем выше стандартное отклонение доходности акции по отношению к доходности рынка, тем выше риск, связанный с данной акцией. Коэффициент корреляции показывает относительную значимость изменчивости. Коэффициент корреляции имеет значения в диапазоне от +1 до –1. Если коэффициент корреляции равен +1, то динамика доходности акции и рынка имеет сильную корреляцию. Таким образом, если стандартное отклонение акции равно 15 %, а рынка – 10 % при коэффициенте корреляции 1, то коэффициент бета составит 1,5.

Коэффициент бета = (Стандартное отклонение доходности акции / Стандартное отклонение доходности рынка) ×

Коэффициент корреляции между доходностью акции рынка =

(0,15 / 0,10) × 1 = 1,5.

Если коэффициент корреляции равен –1, а стандартное отклонение акции и рынка равны соответственно 8 и 10 %, то коэффициент бета равен –0,8:

Коэффициент бета = (0,08 / 0,10) × (–1) = –0,8.

Отрицательный коэффициент корреляции означает, что акция и рынок движутся в противоположных направлениях. Если не существует зависимости между доходностью акции и доходностью рынка, то коэффициент корреляции равен 0. При этом коэффициент бета также равен 0, что означает отсутствие рыночного риска.

Если коэффициент бета акции равен 1, а рынок растет на 20 %, то цена акции повышается на 20 %. Если рынок падает на 20 %, то цена акции также снижается на 20 %. Если рынок имеет коэффициент бета, равный 1, это означает, что данная акция полностью коррелирует с рынком.

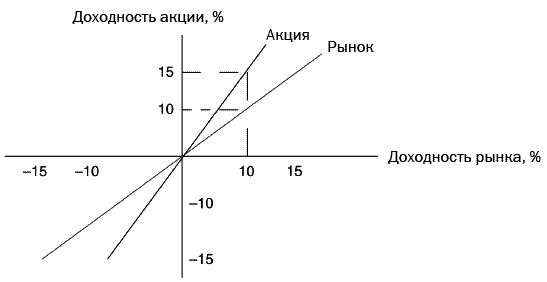
На рис. 12-3 проиллюстрирована связь между акцией с коэффициентом бета, равным 1,5, и рынком с коэффициентом бета, равным 1. Доходность акции составляет 15 %, если рынок растет на 10 %. Акция, имеющая доходность ниже рыночной, находится ниже линии рынка в положительном секторе, а имеющая доходность выше рыночной – в отрицательном секторе. Таким образом, акция, имеющая коэффициент бета выше 1, должна показывать доходность выше средней на растущем рынке и ниже средней – на падающем. Акция с коэффициентом бета ниже 1 менее чувствительна к рыночным колебаниям. Инвесторы, желающие получить повышенную доходность, должны быть готовы к повышенным рискам.

Даже если увеличить степень диверсификации портфеля и приобрести большее количество разнообразных акций, то это не устранит системный риск. Иными словами, акции не защищены от падения рынка. Тем не менее диверсификация не менее чем в 20 различных акций может устранить несистемный риск, т. е. риск, присущий определенной компании. Сюда входят финансовый, деловой риск и риск покупательной способности, влияющие на стоимость акций компании.

Рисунок 12-3

Акция, имеющая коэффициент бета, равный 1,5

Расчет коэффициента бета очень утомительный процесс. Коэффициенты бета отдельных акций можно получить из различных источников, например путем подписки на сервисы Value Line и Standard&Poor’s, а также через финансовые сайты, таких как www.yahoo.com. Не следует беспокоиться, если вы обнаружите, что значения коэффициента бета одной и той же акции на различных ресурсах различаются, поскольку они могут быть рассчитаны на основе различных мер оценки рынка, например индексов S&P 500 или Value Line. Аналогично: расхождения могут быть следствием использования различных временны́х периодов, лежащих в основе вычислений (например, если использовать данные о ценах за трехлетний и пятилетний периоды). Таким образом, не существует единственно верной величины коэффициента бета. В табл. 12-3 приведено сравнение коэффициентов бета акций различных компаний.

Таблица 12-3

Сравнение коэффициентов бета*

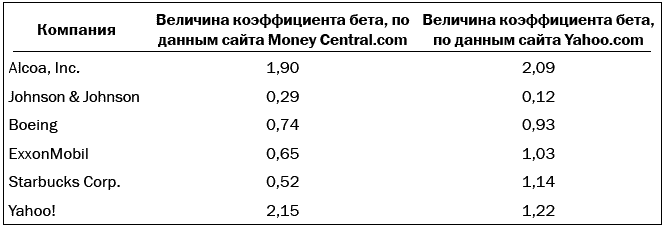
^{* По состоянию на 18 октября 2006 г.}