Покажем, как аукцион с удаленными ставками приводит к оптимальному распределению лотов согласно заявленным предпочтениям. Определим кооперативную игру (L, ν), где L - это множество игроков (7= 0 является закупщиком, а все остальные – участники торгов), а w(S) – это значение коалиции 5. Пусть χ выражает множество возможных распределений лотов (х])_1е1- Если 5 не включает закупщика, тогда w(S) = О/если 5включает закупщика, то

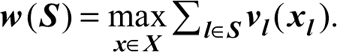
Ядро (L, ν) является множеством всех эффективных распределений π (выигрышей, начисляемых игрокам в зависимости от распределения лотов), которые доступны для большой коалиции и не могут быть блокированы коалицией 5; другими словами, для каждой коалиции 5

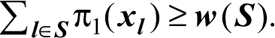
Теорема 1. [Ausubel, Milgrom, 2002; Parkes, Ungar, 2000]. Вектор выигрыша π, образованный в результате удаленного аукциона, является оптимальным эффективным распределением, связанным с заявленными предпочтениями: π є Ядро (L, w).

Оптимальные результаты обладают рядом привлекательных свойств, таких как: 1) эффективность, и 2) конкурентные закупочные затраты покупателя. Следовательно, теорема показывает, что удаленный аукцион не подвергается неэффективному воздействию снижения предложения: ни один участник не может снизить цену, которую он платит за выигранный пакет, удерживая часть проигравших ставок для других пакетов. Теорема также включает идею о конкурентности закупочных затрат покупателя: ни один участник или коалиция участников не желают понижать ставки для поставки лотов. В работе [Ausubel, Milgrom, 2002] (теоремы 2 и 14) определяется результат оптимального распределения, а в работе [Parkes, Ungar, 2000] (теорема 1) авторы независимо доказали эффективность результатов удаленного аукциона, не рассматривая проблему «ядра».

Вектор выигрыша в ядре называется оптимальным для участников, если не существует иного оптимального распределения, которое участники могли бы предпочесть. Если лоты являются субститутами, то итог удаленного аукциона совпадает с результатами аукциона Викри и с единственной оптимальной для участников точкой ядра. Если же лоты не являются субститутами, выигрыш Викри обычно не входит в ядро, а удаленный аукцион приводит результаты с более низкими издержками покупателя.

Теорема 2. [Ausubel, Milgrom, 2002]. Если π – оптимальная для участников точка ядра (L, w), то существует равновесие Нэша полной информации для удаленного аукциона с соответствующим вектором выигрыша π.

Это равновесие достигается с помощью стратегии формы игры: ставка должна равняться реальным затратам плюс неотрицательная константа на каждый пакет. Авторы подчеркивают, что этот вывод относится только к равновесию Нэша в игре полной информации; участникам может понадобиться знание π для расчета стратегии.