По иронии истории Гальтон начал с поисков причинности, а закончил открытием корреляции, отношения, лишенного причинности. Однако все равно признаки каузального мышления остаются в его публикациях. «Легко заметить, что корреляция [между размерами двух органов] должна быть следствием того, что изменчивость двух этих органов отчасти вызвана общими причинами», — пишет он в 1889 году. Первым жертвоприношением на алтарь корреляции стала сложная машина Гальтона для объяснения стабильности распределения генетических признаков в популяции. Доска Гальтона имитировала создание изменчивости по длине тела и ее передачу от поколения к поколению. Но ученому пришлось изобрести наклонные желоба в своей машине, ограничивающие постоянно возрастающее разнообразие в популяции. Не сумев обнаружить биологический механизм, удовлетворительно объясняющий эту силу, возвращающую к среднему, Гальтон просто прервал попытки после восьми лет бесплодных поисков и все внимание сосредоточил на корреляции, как моряк на песне сирены. Статистик Стивен Стиглер, много писавший о Гальтоне, заметил этот неожиданный сдвиг в целях и ожиданиях ученого: «Фигурой умолчания оказались Дарвин, желобки, все это „выживание наиболее приспособленных”. … По жестокой иронии, то, что начиналось как попытка подвести математическую основу под „Происхождение видов”, закончилось тем, что сама суть этой великой работы оказалась отброшена, как ненужная!»

Но для нас, живущих в современную эпоху причинного вывода, исходная проблема остается. Как мы объясним стабильность популяционного среднего, невзирая на дарвиновскую изменчивость, которой одно поколение наделяет последующее?

Возвращаясь к машине Гальтона в свете диаграмм причинности, первое, что я замечаю, — это то, что она была сконструирована неправильно. Постоянно растущей дисперсии, которая вынудила ученого создать ей противовес, вообще не должно было там быть. В самом деле, если мы проследим падение шарика в доске Гальтона с одного уровня на другой, мы увидим, что отклонение на следующем уровне наследует сумму всех отклонений, причиненных всеми булавками, с которыми он сталкивался на своем пути. Это откровенно противоречит уравнению Канемана:

Согласно этим уравнениям, успех в поколении 2 не наследует удачу из поколения 1. Удача по определению преходяща и случайна; она не может влиять на будущие поколения. Но подобное поведение признака несовместимо с устройством машины Гальтона. Чтобы сравнить эти две концепции рядом, нарисуем их ассоциированные диаграммы причинности. На рис. 10а (концепция Гальтона) успех передается через поколения и удача накапливается неограниченно. Это легко себе представить, если под успехом понимать богатство или знатность. Однако для описания наследования физических характеристик, таких как рост, нам придется заменить модель Гальтона той, что на рис. 10б. В ней только генетическая компонента, показанная здесь как талант, передается от одного поколения к другому. Удача действует на каждое поколение независимо, таким образом, что случайные факторы в одном поколении не могут влиять на последующие поколения ни прямо, ни косвенно.

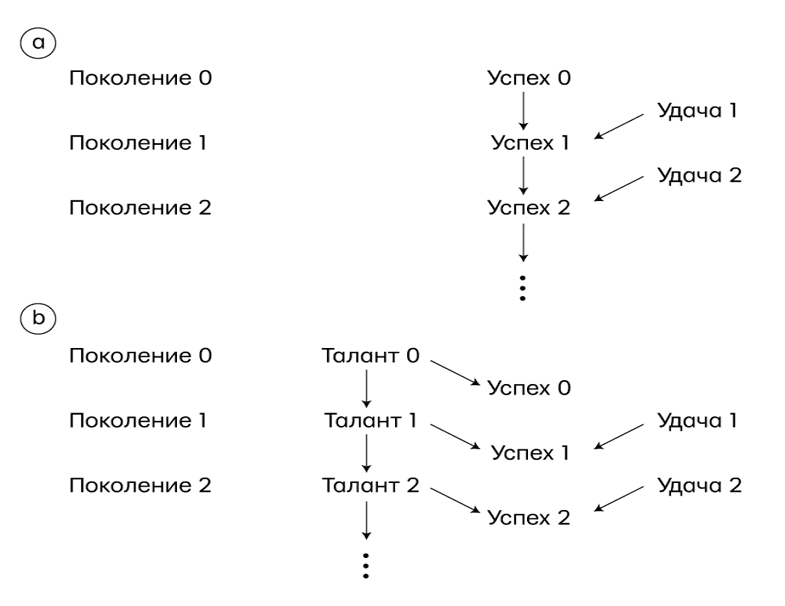
Рис. 10. Две модели наследуемости: а — модель, соответствующая машине Гальтона, в которой удача накапливается от поколения к поколению, приводя ко все возрастающей дисперсии успеха; б — генетическая модель, в которой удача не накапливается, приводит к постоянному разбросу успеха

Обе эти модели совместимы с колоколообразным распределением значений роста. Но первая модель не совместима со стабильностью разброса роста (или успеха). Вторая же модель показывает, что для объяснения стабильности разброса успеха от поколения к поколению нам достаточно объяснить только стабильность генетических факторов в популяции (таланта). Эта стабильность, теперь называемая равновесием Харди — Вайнберга, получила удовлетворительное математическое объяснение в работе Годфри Харолда Харди и Вильгельма Вайнберга 1908 года. И да, они основывались на еще одной каузальной модели — менделевской теории наследственности.

Ретроспективно рассуждая, Гальтон не мог предвидеть достижения Менделя, Харди и Вайнберга. В 1877 году, когда Гальтон прочитал свою лекцию, работа Грегора Менделя 1866 года была основательно забыта (ее вновь открыли только в 1900 году), а математические выкладки доказательства Харди и Вайнберга были бы для него, вероятно, слишком сложны. Однако интересно обратить внимание, как близок он был к верному подходу и как диаграммы причинности легко вскрывают ложность его допущения: передачу случайных факторов, удачи, от одного поколения к другому. К сожалению, его завела в тупик красивая, но неверная причинная модель, а позже, открыв красоту корреляции, он уже решил, что каузальность больше не нужна.

В качестве заключительного личного комментария к истории Гальтона я сознаюсь в смертном для историка грехе, одном из многих грехов, допущенных мной в этой книге. В 1960-х стало немодно писать историю науки с точки зрения современной науки, как я делал выше. Такой стиль исторических заметок, который фокусируется на удачных теориях и экспериментах и уделяет мало внимания неподтвержденным теориям и научным тупикам, теперь именуют издевательским термином «история в стиле вигов». Современный стиль истории науки более демократичен, в нем химики и алхимики пользуются равным уважением, а все теории рассматриваются в социальном контексте своего времени.

Однако, когда приходится объяснять, каким образом причинность была изгнана из статистики, я с гордостью надеваю парик историка-вига. Иначе как надев каузальные очки и пересказав историю Гальтона и Пирсона в свете современной науки о причинах и следствиях, просто невозможно понять, как же статистика стала нечувствительным к типу модели методом редукции данных. На самом деле, поступая так, я выпрямляю искажения, созданные современным большинством историков, которые, не владея каузальным словарем, восхищаются изобретением корреляции и не способны заметить огромную потерю — смерть причинности.