Когда вы впервые сталкиваетесь с контрфактивными величинами, вам может показаться странным, что для выражения непрямого воздействия требуется такой громоздкий математический аппарат. В самом деле, скажете вы, непрямое воздействие — это всего-навсего то, что остается, если вычесть прямое воздействие. Иначе мы могли бы написать:

Если отвечать на это коротко, то схема не работает в моделях, включающих взаимодействия переменных (иногда говорят «модерацию»). Представим, что некое лекарственное средство стимулирует организм выдел ять фермент, который действует как катализатор: он соединяется с этим лекарственным средством и лечит болезнь. Суммарный эффект этого препарата будет, конечно же, положительным. Однако прямой его эффект равен нулю, потому что, если мы заблокируем медиатор (например, не давая организму выделять фермент), препарат не подействует. Непрямой эффект также равен нулю, потому что, если пациент не будет получать препарат, а начнет принимать искусственно синтезированный фермент, болезнь тоже не пройдет. Сам по себе фермент не излечивает болезнь. Таким образом, уравнение (9.4) не выполняется: суммарное воздействие положительное, но и прямое, и непрямое воздействия равны нулю.

Тем не менее уравнение (9.4) выполняется автоматически в одной ситуации без необходимости ввода контрафактивных переменных. Это случай линейной каузальной модели, вроде той, которую мы рассматривали в главе 8. Как обсуждалось там, линейные модели не допускают взаимонаправленных взаимодействий между переменными, и это может быть как преимуществом, так и недостатком. Преимуществом в том смысле, что анализ опосредования становится намного проще, а недостатком — если мы захотим описать некий каузальный процесс в реальном мире, в котором такие взаимодействия все-таки присутствуют.

Поскольку анализ опосредования намного проще для линейных моделей, посмотрим, как он осуществляется, и с чем вероятны проблемы. Допустим, у нас есть каузальная диаграмма, выглядящая как рис. 59. Поскольку мы работаем с линейной моделью, мы можем представить силу каждого воздействия одним числом. Метки (путевые коэффициенты) показывают, что увеличение переменной экспериментальное воздействие на 1 единицу увеличит переменную медиатор на 2 единицы. Аналогично увеличение переменной медиатор на 1 единицу увеличит переменную итог на 3 единицы, а увеличение экспериментального воздействия на 1 единицу увеличит итог на 7 единиц. Все это прямые воздействия. Здесь мы подходим к первой причине того, почему линейные модели так просты: прямые воздействия не зависят от уровня опосредующей переменной, т. е. КПВ (m) одно и то же для всех значений m и мы можем говорить о единственном прямом воздействии.

Каково же будет суммарное воздействие интервенции, благодаря которой экспериментальное воздействие увеличится на 1 единицу? Во-первых, эта интервенция напрямую вынуждает итог увеличиться на 7 единиц (если мы удерживаем медиатор на постоянном уровне). Она также увеличивает медиатор на 2 единицы. Наконец, поскольку каждое увеличение медиатора на 1 единицу напрямую вызывает увеличение итога на 3 единицы, увеличение медиатора на 2 единицы приведет к дополнительному увеличению итога на 6 единиц. Поэтому суммарное увеличение итога по обоим каузальным путям будет составлять 13 единиц. Первые 7 единиц соответствуют прямому воздействию, а оставшиеся 6 — непрямому воздействию. Проще пареной репы!

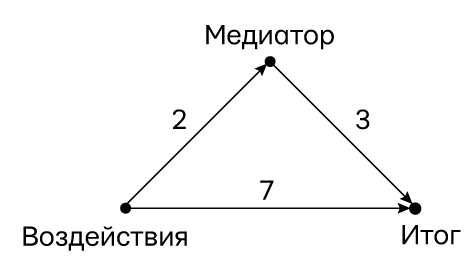
Рис. 59. Пример линейной модели (путевая диаграмма) с опосредующей переменной

Итак, если имеется более одного непрямого пути от X к Y, мы оцениваем непрямое воздействие по каждому пути как произведение всех путевых коэффициентов вдоль этого пути. Затем мы получаем суммарное непрямое воздействие, суммируя все непрямые каузальные пути. В итоге суммарное воздействие X на Y равняется сумме прямых и непрямых воздействий. Это правило суммы произведений используется с тех пор, как Сьюалл Райт изобрел путевой анализ, и, строго говоря, оно действительно следует из определения суммарного взаимодействия в терминах do-оператора.

В 1986 году Рубен Барон и Дэвид Кенни сформулировали набор принципов для обнаружения и оценки опосредования в системе уравнений. Основные принципы заключаются, во-первых, в том, что все переменные связаны линейными уравнениями, которые оцениваются путем подбора их в соответствии с данными. Во-вторых, прямые и непрямые воздействия исчисляются путем подбора двух уравнений, соответствующих данным: одного с опосредующей переменной и другого без нее. Значительное изменение коэффициентов в случае, когда вводится опосредующая переменная, считается доказательством наличия опосредования.

Простота и убедительность метода Барона — Кенни снискала ему заслуженные лавры в среде общественных наук. В 2014 году их статья занимала 33-е место сверху в списке самых цитируемых работ за всю историю. Их цитировали чаще, чем Альберта Эйнштейна, чаще, чем Зигмунда Фрейда, чаще почти любого другого ученого, которого только можно вспомнить. Их статья стоит на втором месте среди всех публикаций по психологии и психиатрии, хотя она совсем не о психологии. Она о некаузальном опосредовании.

Беспрецедентная популярность подхода Барона — Кенни, без сомнения, определяется двумя факторами. Во-первых, опосредование — очень востребованная концепция. Наше желание понять, «как действует природа» (т. е. найти M в X → M → Y), вероятно, даже сильнее, чем желание подсчитать его. Во-вторых, этот метод легко редуцируется до процедуры, по простоте подобной кулинарному рецепту, основанной на знакомых концепциях статистики, дисциплины, которая долгое время претендовала на исключительное право на объективность и эмпирическую правомерность. Поэтому почти никто не заметил случившийся при этом гигантский рывок вперед — тот факт, что каузальная величина (опосредование) была определена и оценена чисто статистическими методами.

Тем не менее первые трещины в этом возведенном из регрессий оборонительном сооружении начали появляться еще в начале 2000-х, когда практики попытались обобщить правило суммы произведений для нелинейных систем. Это правило включает два допущения: воздействия вдоль разных путей аддитивны, а путевые коэффициенты вдоль одного пути перемножаются, и оба они приводят к неверным ответам в нелинейных моделях, как мы увидим ниже.

Это заняло немало времени, но в конце концов практикующие анализ опосредования окончательно пришли в себя. В 2001 году мой покойный друг и коллега Род Макдональд писал: «Я полагаю, что лучший способ обсудить вопрос обнаружения или демонстрации модерации или медиации в регрессии — это отложить всю имеющуюся по этому поводу литературу в сторону и начать с нуля». Самые свежие публикации по опосредованию, похоже, последовали совету Макдональда: контрфактивные и графические методы в них используются более часто и последовательно, чем регрессионный подход. А в 2014 году основоположник метода Барона — Кенни Дэвид Кенни опубликовал новый раздел на своем веб-сайте под названием «Каузальный анализ опосредования». Хотя я бы пока поостерегся назвать его обращенным, Кенни явно осознает, что времена меняются и анализ опосредования вступает в новую эпоху.

Теперь давайте рассмотрим простой пример того, как наши ожидания оказываются неверными, стоит нам только выйти за границы Линейной Страны Чудес. Рассмотрим рис. 60, представляющий собой слегка измененный рис. 59, на котором кандидат на рабочее место решает принять предложение тогда и только тогда, когда обещанное жалование превосходит определенную пороговую сумму, в нашем случае 10 единиц. Предложение по зарплате определяется так, как показано на диаграмме: 7 × образование + 3 × навык. Обратите внимание, что функции, определяющие навык и зарплату, все еще предполагаются линейными, но отношение жалованья к итогу нелинейно, потому что у него есть пороговый эффект.

Давайте подсчитаем для этой модели суммарное, прямое и непрямое воздействия, ассоциированные с увеличением образования на 1 единицу. Суммарное воздействие определенно равно 1, поскольку когда образование меняется с 0 на 1, зарплата поднимается с 0 до (7 ∙ 1) + (3 ∙ 2) = 13, что больше порогового значения в 10, и таким образом итог меняется с 0 на 1.

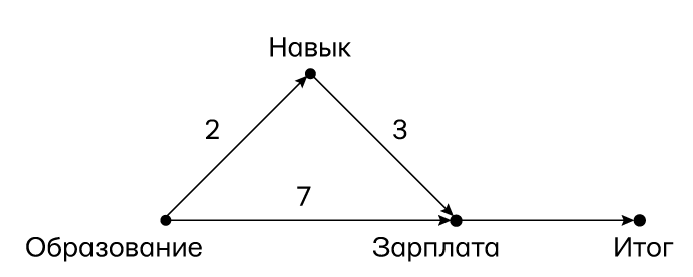
Рис. 60. Опосредование, совмещенное с пороговым эффектом

Вспомним, что натуральное непрямое воздействие — это ожидаемое изменение итога, при учете, что мы не меняем образование, но устанавливаем навык на тот уровень, который он бы принял, если мы увеличили бы образование на 1. Легко увидеть, что в этом случае зарплата увеличивается с 0 до 2 ∙ 3 = 6. Это ниже, чем пороговое значение 10, поэтому податель заявления откажется и ННВ = 0.

Что же насчет прямого воздействия? Как упоминалось выше, вопрос в том, на каком уровне нам следует удерживать опосредующую переменную. Если навык оставить на том уровне, который был до того, как мы изменили образование, тогда зарплата изменится с 0 до 7 и итог = 0. Таким образом, КПВ (0) = 0. Однако, если мы придадим навыку то значение, которое он получает после изменения образования (а именно 2), зарплата изменится с 6 до 13. Это меняет итог с 0 на 1, потому что 13 выше порогового значения для подателя заявления, и он согласится на работу. Итак, КПВ (2) = 1.

Следовательно, прямое воздействие равно 0 или 1 в зависимости от постоянного значения, которое мы придаем опосредующей переменной. В отличие от Линейной Страны Чудес выбор значения медиатора играет огромную роль, и у нас возникает дилемма. Если мы желаем сохранить аддитивный принцип, суммарное воздействие = прямое воздействие + непрямое воздействие, нам придется использовать КПВ (2) в качестве определения каузального воздействия. Но это выглядит слишком произвольно и в чем-то даже ненатурально. Если мы предполагаем изменить переменную образование и хотим узнать ее прямое воздействие, мы, скорее всего, оставим переменную навык на том уровне, который у нее был. Другими словами, интуитивно кажется более оправданным использовать в качестве прямого воздействия КПВ (0). Более того, это согласуется с натуральным прямым воздействием в этом примере. Однако тогда мы теряем аддитивность: суммарное воздействие не равно сумме прямого и непрямого воздействий.

Тем не менее — вопреки ожидаемому — несколько видоизмененная разновидность аддитивности сохраняется, не только здесь, но и вообще. Читателям, которые не испугаются небольших подсчетов, возможно, будет интересно сосчитать ННВ для возврата от X = 1 до X = 0. В этом случае зарплата падает с 13 до 7 и итог меняется с 1 на 0 (т. е. податель заявления отказывается от предложения). Подсчитанное в обратном направлении ННВ = –1.0 Восхищение вызывает тот факт, что суммарное воздействие (X = 0 → X = 1) = НПВ (X = 0 → X = 1) — ННВ (X = 1 → X = 0), или в этом случае 1 = 0 — (–1). Вы видите версию аддитивного принципа для натуральных воздействий, только в данном случае это оказывается субстрактивный (вычитательный) принцип! Я был невероятно счастлив, когда из анализа стал вырисовываться такой вариант аддитивности, несмотря на нелинейность уравнений.

Немало чернил ушло на споры о самом «правильном» способе обобщения прямых и непрямых воздействий при переходе от линейных к нелинейным моделям. К сожалению, большая часть статей подходит к проблеме с конца. Вместо того чтобы заново, с нуля решить, что мы имеем в виду под прямым и непрямым воздействиями, они начинают с предположения, что нам всего-то нужно немного подправить определения для линейных моделей. Например, в Линейной Стране Чудес мы видели, что непрямое воздействие подается как произведение двух путевых коэффициентов. Поэтому некоторые исследователи попытались определить непрямое воздействие как произведение двух численных выражений, из которых одно измеряет воздействие X на M, а второе — воздействие M на Y. Этот подход стал известен как метод произведения коэффициентов. Однако мы также видели, что в Линейной Стране Чудес непрямое воздействие задается разницей между суммарным воздействием и прямым воздействием. Поэтому другая, не менее самоотверженная группа исследователей определяла непрямое воздействие как разницу двух численных показателей, один из которых отражал суммарное воздействие, а другой — прямое воздействие. Этот метод стал называться методом разницы коэффициентов.

Какой же из них верен? Ни тот ни другой! Обе группы исследователей спутали процедуру и смысл. Процедура здесь математическая: смысл каузальный. На самом деле проблема еще глубже: исследователи, занимающиеся регрессионным анализом, никогда не рассматривали смысл непрямого воздействия за рамками пузыря линейных моделей. Единственным значением понятия непрямого воздействия был результат алгебраической процедуры (перемножить путевые коэффициенты). Когда эту процедуру у них отобрали, их стало носить ветром, как лодку без якоря.

Один из читателей моей книги «Причинность» в своем письме ко мне прекрасно описывает это чувство растерянности. Мелани Уолл (Колумбийский университет) в свое время преподавала курс математического моделирования биостатистикам и медикам. Однажды она, как обычно, объясняла студентам, как вычислять непрямое воздействие, перемножая прямые путевые коэффициенты. Некий студент спросил ее, что именно имеется в виду под непрямым воздействием. «Я ответила ему то, что отвечала всегда, что непрямое воздействие — это воздействие, которое изменение в X производит на Y через его взаимоотношения с опосредующей переменной Z», — написала мне Уолл. Однако студент оказался очень настойчивым. Он вспомнил, как преподаватель объяснял прямое воздействие как воздействие, которое остается, если мы будем поддерживать опосредующую переменную на постоянном уровне, и спросил: «Тогда что мы удерживаем на постоянном уровне, когда говорим о непрямом воздействии?»

Уолл не знала, что сказать. «Я не уверена, что у меня сейчас есть хороший ответ на этот вопрос, — ответила она. — Как насчет того, что я выясню, что смогу, и сообщу вам?»

Это было в октябре 2001 года, всего через четыре месяца после того, как я представил статью по каузальному опосредованию на конференции «Неопределенность в искусственном интеллекте» в Сиэтле. Стоит ли говорить, что мне очень хотелось поразить Мелани своим свежим решением ее задачи, и я написал ей то же, что пишу здесь сейчас для вас: «Непрямое воздействие X на Y — это изменение в Y, которое мы наблюдаем, если удерживаем X на постоянном уровне и в то же время изменяем M до такого уровня, который M приняло бы при изменении X на единицу».

Я не уверен, что Мелани впечатлилась моим ответом, но ее любознательный студент заставил меня серьезно задуматься о том, как прогрессирует наука в наши времена. Вот сейчас, думал я, прошло 40 лет с тех пор, как Блалок и Дункан ввели путевой анализ в общественные науки. Десятки учебников и сотни научных публикаций по прямым и непрямым воздействиям выходят из печати каждый год, некоторые из них — с заголовками-оксюморонами вроде «Регрессионный подход к опосредованию». Каждое поколение передает следующему из рук в руки мудрость о том, что непрямое воздействие — это всего лишь произведение двух других воздействий, или же разница между суммарным и прямым воздействиями. Никто не осмеливается задать простой вопрос: но что это самое непрямое воздействие означает? Чтобы задать его, вдребезги разбив нашу веру в пророческую роль научного консенсуса, понадобился невинный студент с беззастенчивым нахальством мальчишки из андерсеновского «Нового платья короля».