Несмотря на раннюю работу Бёркс, спустя полстолетия статистикам все еще было сложно даже выразить саму идею прямых и непрямых воздействий, не говоря уже о том, чтобы оценить их. Пример, которым я проиллюстрирую это, похож на парадокс Симпсона, но с хитрым вывертом.

В 1973 году Юджин Хаммель, заместитель декана в Калифорнийском университете, обнаружил тревожную тенденцию в соотношении мужчин и женщин среди поступающих в вуз. Согласно его данным, из подающих документы в высшую школу Беркли мужчин зачислили 44 %, в то время как из числа абитуриентов-женщин зачислили только 35 %. В то время дискриминация по полу начала привлекать широкое общественное внимание, и Хаммель не хотел сидеть сложа руки до тех пор, пока у кого-нибудь не появятся по этому поводу вопросы. Он решил исследовать причины такой диспропорции.

Решения по зачислению абитуриентов в Беркли, как и в других университетах, принимаются отдельными факультетами, а не университетом в целом. Поэтому показалось разумным рассмотреть данные по поступлениям по отдельным факультетам. Однако, сделав это, Хаммель обнаружил удивительный факт. Оказалось, что на каждом отдельном факультете решения приемной комиссии были в пользу женщин, а не мужчин. Как это вообще возможно?

На этом этапе Хаммель поступил разумно: он пригласил профессионала в статистике. Питер Бикель, которого попросили посмотреть на эти данные, немедленно понял, что перед ним разновидность парадокса Симпсона. Как мы видели в главе 6, это тенденция, которая направлена в одну сторону в каждой отдельной группе данной популяции (в приведенном случае каждый факультет предпочитает зачислять женщин), но в противоположную сторону, если рассматривать всю популяцию в целом (в целом по университету видимые предпочтения оказываются мужчинам). В главе 6 мы также видели, что правильное решение парадокса очень зависит от вопроса, которым мы задаемся. В этом случае вопрос ясен: виновен ли университет (или кто-то из сотрудников университета) в сознательной дискриминации женщин?

Когда я впервые рассказал своей жене об этом случае, первой ее реакцией было: «Этого не может быть. Если каждый отдельный факультет дискриминирует мужчин, университет в целом не может дискриминировать женщин». И она была права! Этот парадокс задевает наше понимание дискриминации, которое представляет собой каузальную концепцию, включающую преференции в связи с заявленным полом абитуриента. Если все участники предпочитают один пол другому, вся группа в целом должна демонстрировать те же предпочтения. Если кажется, что данные свидетельствуют об обратном, это означает, что мы обрабатываем данные неправильно, а не в соответствии с логикой причинности. Только с такой логикой и с внятной каузальной схемой мы определим, виновен университет или нет.

На самом деле Бикель и Хаммель сумели найти каузальную схему, которая их полностью удовлетворила. Они написали об этом статью, опубликованную в журнале «Сайенс» в 1975 году, предположив простое объяснение: абитуриентов-женщин отвергали чаще просто потому, что они подавали заявления на факультеты, на которые вообще сложнее поступить.

Если подробнее, то на факультеты гуманитарных и общественных наук пытаются поступить в основном абитуриенты женского пола. На этих факультетах они сталкиваются с двойной неприятностью: число подающих документы на них больше, а число мест — меньше. В свою очередь, женщины намного реже подавали документы на факультеты вроде инженерной механики, куда поступить было легче. У этих факультетов было больше денег и больше мест для студентов, короче говоря, больший процент подавших документы оказывался принят.

Почему женщины подавали документы на те факультеты, на которые сложнее поступить? Возможно, от поступления на технические факультеты их отпугивало то, что на них требуется лучше знать математику, или то, что они традиционно воспринимаются как «мужские». Вероятно, это результат дискриминации на более ранних стадиях обучения: общество имело тенденцию отталкивать женщин от технических дисциплин, пример Барбары Бёркс недвусмысленно это демонстрирует. Но указанные обстоятельства университет Беркли не мог изменить, поэтому дискриминации со стороны вуза не было. Бикель и Хаммель подвели итог: «Университет в целом не причастен к дискриминации против абитуриентов-женщин».

Я хочу хотя бы вкратце отметить точность языка, использованного Бикелем в этой статье. Он проводит тщательные различия между двумя терминами, которые в бытовом английском часто кажутся синонимами: bias («перекос») и discrimination («дискриминация»). Он определяет перекос как «характер ассоциации между конкретным решением и полом конкретного абитуриента». Обратите внимание на слова «характер ассоциации». Они говорят нам о том, что перекос — явление первой ступени Лестницы Причинности. В свою очередь, дискриминацию он характеризует как «принятие решения в зависимости от пола абитуриента тогда, когда это не имеет отношения к квалификационным требованиям для зачисления». Формулировки «принятие решения», «в зависимости от», «не имеет отношения» просто благоухают причинностью, несмотря на то что Бикель в 1975 году еще не мог решиться произнести это слово вслух. Дискриминация, в отличие от перекоса, находится на второй или третьей ступени Лестницы Причинности.

Анализируя данные, Бикель почувствовал, что они должны быть разделены на страты по факультетам, потому что именно отдельные факультеты были тем уровнем, на котором принимались решения. Было ли это правильно? Чтобы ответить на этот вопрос, начнем с того, что нарисуем каузальную диаграмму (рис. 56). Весьма полезно также посмотреть, как определяет дискриминацию американское прецедентное право. Оно использует контрфактивную терминологию, и это явный признак того, что мы поднялись на третью ступень Лестницы Причинности. В деле Карсона против Вифлеемской сталелитейной корпорации (1996) апелляционный суд седьмого округа писал: «Центральный вопрос в любом деле о дискриминации при приеме на работу заключается в том, предпринял бы наниматель такое же действие, если бы кандидат был человеком другой расы (возраста, пола, вероисповедания, этнического происхождения и т. д.), а все остальное было бы таким же». Это определение четко выражает идею, что мы должны заблокировать, или «заморозить», все каузальные пути, которые ведут от пола к зачислению через любые другие переменные (например, квалификация, предпочитаемые факультеты и т. д.). Другими словами, дискриминация равна прямому воздействию пола на исход решения о зачислении.

Ранее мы видели, что введение поправок по медиатору неправомерно, если мы хотим оценить общее воздействие одной переменной на другую. Но в случае дискриминации, согласно решению суда, имеет значение не общее, а прямое воздействие. Таким образом, решение Бикеля и Хаммеля оправдано: при допущениях, показанных на рис. 56 они совершенно верно разделили данные по отдельным факультетам, и их результаты представляют собой обоснованную оценку прямого воздействия пола на зачисление. Им удалось успешно справиться с задачей, несмотря на то что терминология прямых и непрямых воздействий не была доступна Бикелю в 1973 году.

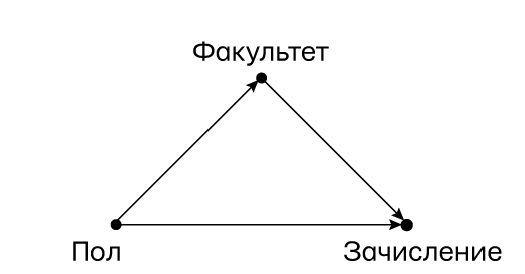
Рис. 56. Каузальная диаграмма для парадокса с зачислением в Калифорнийский университет в Беркли (простая версия)

Однако самое интересное в этой истории — не исходная статья, написанная Бикелем и Хаммелем, а дискуссия, которая последовала за ней. После публикации статьи Уильям Крускал из Университета Чикаго написал Бикелю письмо, утверждая, что их объяснение на самом деле не снимает обвинений с Беркли. На самом деле Крускал задался вопросом, насколько вообще любое исследование, основанное исключительно на наблюдениях (в противоположность РКИ) на это способно.

Для меня их переписка — просто невероятное явление. Не так часто нам удается увидеть, как два великих ума сражаются с концепцией (в данном случае с причинностью), для описания которой у них нет адекватного словаря. Позднее Бикель продолжит тему и выиграет «грант гения» от Фонда Макартуров в 1984 году. Но в 1975 году он был еще только в начале своей карьеры, и для него было одновременно честью и вызовом схлестнуться с Крускалом, настоящим великаном в американском статистическом сообществе.

В своем письме к Бикелю Крускал указал на то, что в отношениях между факультетом и результатом зачисления может быть неизмеримый осложнитель, такой как место проживания. Он предоставил численный пример, представляющий гипотетический университет с двумя факультетами, дискриминирующими по полу, в которых данные в результате полностью совпадают с данными в примере Бикеля. Он добился этого, предположив, что оба факультета принимают всех мужчин, живущих в том же штате, и всех женщин из других штатов, и отвергают всех мужчин из других штатов и женщин из того же штата, и это у них единственный критерий для принятия решения о зачислении. Разумеется, такая политика зачисления студентов будет грубым, азбучным примером дискриминации. Но поскольку общие числа принятых и отвергнутых абитуриентов каждого пола были точно такими же, как в примере Бикеля, то по логике последнего пришлось бы признать, что дискриминации нет. Согласно Крускалу, факультеты только кажутся невиновными, потому что Бикель вводил поправки лишь по одной переменной вместо двух.

Крускал указал пальцем на самое слабое место в статье Бикеля: отсутствие четко оправданного критерия, по каким переменным вводить поправки. Крускал не предложил никакого решения, и на самом деле в его письме чувствуется отчаяние от неверия, что оно в принципе реально.

В отличие от Крускала, мы можем нарисовать диаграмму и ясно увидеть, в чем заключается проблема. На рис. 57 представлена диаграмма, соответствующая контрпримеру Крускала. Не кажется ли она вам чем-то знакомой? Так и должно быть! Это совершенно та же диаграмма, что и нарисованная в 1926 году Барбарой Бёркс, только переменные в ней другие.

Тут просится на язык американская пословица «Великие умы мыслят схоже», но, возможно, вернее было бы сказать, что великие проблемы привлекают внимание великих умов.

Крускал утверждал, что при анализе в этой ситуации нужно вводить поправки как по переменной факультет, так и по штату проживания, и взгляд на рис. 57 объясняет, почему это так. Чтобы заблокировать все пути, кроме прямого, мы должны стратифицировать данные по факультетам. Таким образом мы закроем непрямые пути пол → факультет → результаты зачисления. Но, сделав это, мы открываем побочный путь пол → факультет ← штат проживания → результаты зачисления из-за переменной схождения факультет. Если мы также введем поправки по переменной штат проживания, то закроем этот путь, и поэтому все оставшиеся корреляции должны быть обусловлены прямым (дискриминационным) путем пол → результаты зачисления. За отсутствием диаграмм Крускалу пришлось убеждать Бикеля числами, и на самом деле его числа показали то же самое. Если мы вообще не вводим никаких поправок, то процент зачисляемых женщин ниже. Если мы вводим поправки по факультету, то у женщин процент зачисления кажется выше. Если мы вводим поправки и по факультету, и по штату проживания, числа снова покажут более низкий процент зачисления для женщин.

Рис. 57. Каузальная диаграмцма для парадокса зачислений в Калифорнийский университет в Беркли (версия Крускала)

Подобные аргументы показывают нам, почему концепция опосредования вызывала ранее (и до сих пор вызывает) такие подозрения. Она выглядит нестабильной и неуловимой. Результаты зачисления оказываются настроены против женщин, потом против мужчин, потом снова против женщин. В своем ответе Крускалу Бикель продолжал настаивать, что поправка по месту, где принимаются решения (факультет) чем-то отличается от поправки по критерию этого решения (штат проживания). Однако 100 %-ной уверенности, судя по всему, у него по этому поводу не было. Он спрашивает несколько беспомощно: «Здесь я вижу нестатистический вопрос: что такое перекос?» Почему знак перекоса меняется в зависимости от того, как мы его измеряем? На самом деле его идея принципиального различия между перекосом и дискриминацией была верна. Перекос, искажение — это скользкое статистическое понятие, которое может исчезнуть, если нарезать данные не вдоль, а поперек. Дискриминация, как причинностная концепция, отражает реальность, и поэтому должна оставаться неизменной вне зависимости от способа обработки данных.

Фраза, которой не хватало в словаре у них обоих, — «оставаться постоянной». Чтобы заблокировать непрямой путь от пола к результатам зачисления, мы должны зафиксировать значение переменной факультет и «покрутить» переменную пол. Когда переменная факультет принимает фиксированное значение, мы (фигурально выражаясь) не даем абитуриентам выбирать, на какой факультет подавать документы. Поскольку в статистике нет слова для этого понятия, обычно делается нечто с виду похожее: вводится поправка по переменной факультет. Именно это сделал Бикель: он стратифицировал данные по факультетам и заключил, что дискриминации нет. Эта процедура законна, когда переменные факультет и результаты зачисления не имеют осложнителей; в этом случае «видеть» и «делать» — одно и то же. Но Крускал совершенно корректно спросил: «А что, если там есть осложнитель, например штат проживания?» Он, вероятно, и не осознавал, что шел по следам Бёркс, нарисовавшей точно такую же диаграмму.

Невозможно даже передать, насколько часто эта ошибка появлялась в рассуждениях долгие годы — по опосредующей переменной вводились поправки, вместо того чтобы придать ей постоянное значение. По этой причине я называю ее Заблуждением Опосредования. Безусловно, это заблуждение безобидно, если ни опосредующая, ни итоговая переменные не осложнены. Но если осложнители присутствуют, результаты анализа могут привести к совершенно противоположным выводам, как показал численный пример Крускала. Он демонстрирует, как легко исследователь может прийти к выводу об отсутствии дискриминации там, где она есть.

Бёркс и Крускал были исключениями своего времени, признавая Заблуждение Опосредования ошибкой, хотя они и не предлагали для него верного решения. Р. Э. Фишер пал жертвой этого же заблуждения в 1936 году, и сейчас, 80 лет спустя, статистика все еще не справилась с этой проблемой. К счастью, со времен Фишера наблюдается значительный прогресс. Так, эпидемиологи знают, что необходимо следить за осложнителями на пути между опосредующей переменной и итоговой. Однако есть и те, кто отказывается от языка диаграмм (как некоторые экономисты до сих пор), они жалуются и признаются, что для них объяснить, что означает это предупреждение, — просто пытка.

Хорошо, что проблема, которую Крускал однажды назвал «возможно, принципиально неразрешимой», была решена два десятилетия назад. У меня есть странное чувство, что Крускалу это решение понравилось бы, и в своем воображении я демонстрирую ему мощь do-исчисления и контрфактивной алгоритмизации. К сожалению, он вышел на пенсию в 1990 году, как раз тогда, когда правила do-исчисления постепенно формировались, и умер в 2005 году.

Я уверен, что некоторым читателям интересно, чем в итоге закончилось дело с университетом Беркли. Отвечу: ничем. Хаммель и Бикель были убеждены, что университету не о чем беспокоиться, и, действительно, никаких судебных процессов или федеральных расследований в итоге не проводилось. Данные намекали на обратную дискриминацию, в пользу женщин, и на самом деле этому были явные свидетельства: «В большинстве случаев, в которых женщинам оказывались предпочтения, дело, похоже, обстояло таким образом, что приемные комиссии старались преодолеть многолетний недостаток женщин в их областях науки», — писал Бикель. Всего спустя три года дело об антидискриминационных мерах против другого кампуса Калифорнийского университета дошло до Верховного суда. Если бы Верховный суд отменил антидискриминационные меры, подобные «льготы для женщин» стали бы противозаконными. Однако Верховный суд поддержал их, и случай с Беркли стал исторической вехой.

Истинный мудрец оставит последнее слово не за Верховным судом, а за своей женой. Почему у моей супруги было такое сильное интуитивное убеждение, что университет в целом не может дискриминировать кого-либо, если все его факультеты действуют честно? Это теорема каузального исчисления, похожая на принцип «само собой разумеется». Этот принцип в том виде, в каком его постулировал Леонард Джимми Сэвидж, относится к общему воздействию, в то время как данная теорема верна для прямого воздействия. Само определение прямого воздействия опирается на суммирование прямых воздействий в субпопуляциях.

Коротко и ясно — честность на каждом отдельном месте составляет общую честность. Моя жена была права.