В начале 1980-х проектирование искусственного интеллекта зашло в тупик. С тех пор как Алан Тьюринг впервые изложил задачу в статье 1950 года «Вычислительные машины и интеллект», ведущим подходом в этой области были так называемые системы на основе правил или экспертные системы, которые организуют человеческое знание как набор конкретных и общих фактов и используют правила логического вывода, чтобы связать их. Например: Сократ — человек (конкретный факт). Все люди смертны (общий факт). Из этой базы знаний мы (или разумная машина) можем вывести тот факт, что Сократ смертен, используя универсальное правило логического вывода: если все A являются B и x является A, то x является B.

Теоретически это был годный подход, но жесткие правила вряд ли могут отразить знания из реальной жизни. На деле мы все время сталкиваемся с исключениями из правил и неопределенностями в данных, даже когда этого не осознаем. К 1980 году стало ясно, что экспертным системам трудно делать правильные выводы из неопределенных знаний. Компьютер не мог воспроизвести процесс, с помощью которого человек-специалист приходит к логическому выводу, потому что сами специалисты не могли выразить свой мыслительный процесс на языке, доступном системе.

Таким образом, конец 1970-х был временем брожения умов: сообщество исследователей ИИ пыталось найти способ справиться с неопределенностью. В идеях недостатка не было. Лотфи Заде из Калифорнийского университета в Беркли предложил «нечеткую логику», в которой утверждения, не являясь ни истинными, ни ложными, принимают ряд возможных значений истинности. Гленн Шейфер из Канзасского университета предложил «функции убеждений», которые приписывают каждому факту две вероятности: одна указывает, насколько вероятно, что он «возможен», другая — насколько вероятно, что он «доказуем». Эдвард Фейгенбаум и его коллеги из Стэнфордского университета попробовали работать с «факторами достоверности», добавив числовые меры неопределенности в детерминистские правила логического вывода.

К сожалению, несмотря на всю изобретательность, эти подходы имели общий недостаток: они моделировали эксперта, а не мир и поэтому нередко давали непредвиденные результаты. Например, они не могли работать одновременно в диагностическом и прогностическом режимах, что является бесспорным преимуществом правила Байеса. При подходе, основанном на факторе определенности, правило «Если огонь, то дым (с определенностью c₁)» не может согласованно сочетаться с утверждением «Если дым, то огонь (с определенностью c₂)», не вызывая бесконтрольного роста уверенности.

В то время также рассматривался подход, основанный на вероятностях, однако он сразу приобрел дурную славу из-за огромных потребностей в памяти для хранения и очень долгого времени обработки. Я вышел на арену довольно поздно, в 1982 году, с очевидным, но радикальным предложением: вместо того чтобы заново изобретать теорию неопределенности с нуля, оставим вероятность в качестве защитницы здравого смысла и просто исправим ее недостатки в вычислительном плане. А именно, вместо того чтобы представлять вероятность в огромных таблицах, как это делали раньше, выразим ее в виде сети слабо связанных переменных. Если мы разрешим каждой переменной взаимодействовать только с несколькими соседними, это позволит преодолеть вычислительные препятствия, которые помешали другим исследователям вероятностей.

Эта идея пришла ко мне не во сне; она почерпнута из статьи Дэвида Румельхарта, когнитивиста из Калифорнийского университета в Сан-Диего и пионера в проектировании нейросетей. Его статья о детском чтении, опубликованная в 1976 году, показала, что это сложный процесс, в ходе которого нейроны на многих разных уровнях действуют одновременно (рис. 15). Одни нейроны распознают отдельные особенности — круги или линии. Над ними другой слой нейронов объединяет эти формы и строит предположения о том, что за буква получается из них.

На рис. 15 показано, как нейросеть борется с большой долей неопределенности применительно ко второму слову. На уровне букв это может быть FHP, но на уровне слов такое сочетание не имеет особого смысла. Здесь предположительны FAR, CAR или FAT. Нейроны переводят информацию на синтаксический уровень, который определяет, что после слова THE ожидается существительное. Наконец, эта информация полностью передается на семантический уровень, где учитывается, что в предыдущем предложении упоминался VolksWagen, а значит, искомым сочетанием будет THE CAR (ЭТА МАШИНА), относящееся к тому самому Volkswagen. Важнее всего здесь, что нейроны передают информацию туда и обратно, сверху вниз, снизу вверх и из стороны в сторону. Это система со многими параллельными процессами, которая сильно отличается от нашего представления о мозге как о монолитной системе с централизованным управлением.

Читая статью Румельхарта, я убеждался в том, что любой искусственный интеллект должен будет моделировать себя на основе наших знаний о нейронной обработке информации у человека и что машинное мышление в условиях неопределенности должно использовать похожую архитектуру передачи сообщений. Но что же это за сообщения? На понимание этого у меня ушел не один месяц. И наконец я осознал, что эти сообщения были условными вероятностями в одном направлении и отношениями правдоподобия в другом.

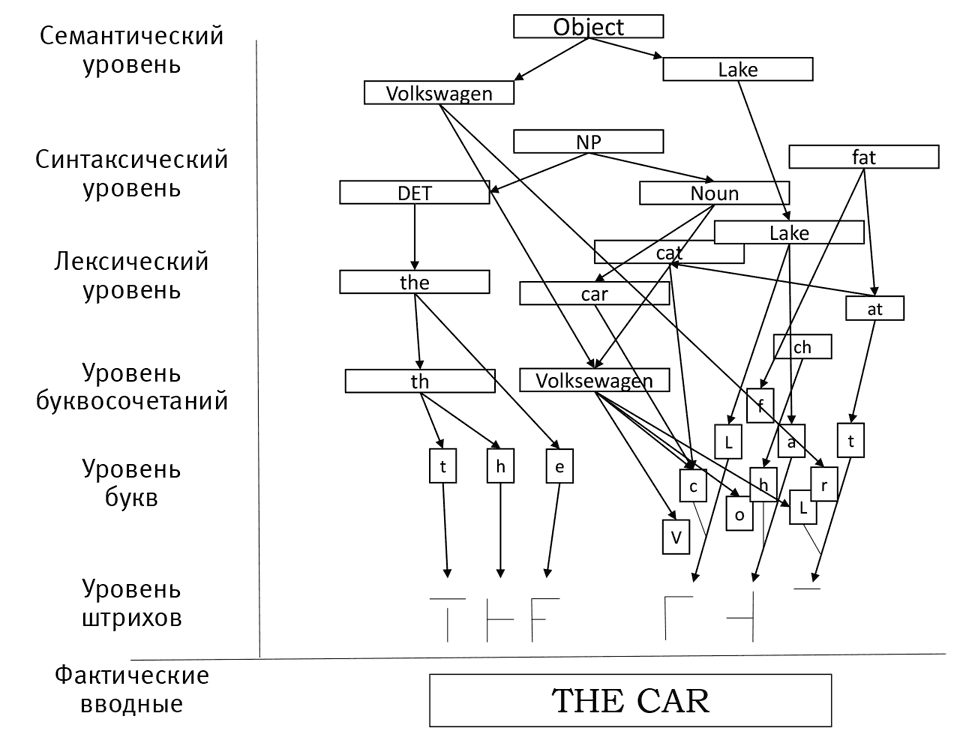
Рис. 15. Набросок Дэвида Румельхарта показывает, как сеть передачи сообщений учится читать сочетание THE CAR (источник: любезно предоставлено Центром исследований мозга и познания Калифорнийского университета в Сан-Диего)

Точнее, я предполагал, что сеть будет иерархической — со стрелками, ведущими от верхних нейронов к нижним или от «родительских узлов» к «дочерним узлам». Каждый узел будет отправлять всем соседям (как выше, так и ниже в иерархии) сообщение о своей текущей степени уверенности в переменной, которую отслеживает (например, «Я на две трети уверен, что эта буква — R»). Получатель будет обрабатывать сообщение двумя разными способами, в зависимости от его направления. Если сообщение идет от «родителя» к «ребенку», то «ребенок» обновит степень уверенности, используя условные вероятности, подобные тем, которые мы видели в образце с чайной. Если сообщение передается от «ребенка» к «родителю», то родитель обновит свою степень уверенности, умножив их на отношение правдоподобия, как в случае с маммограммой.

Повторное применение этих двух правил к каждому узлу в сети называется распространением степени уверенности. В ретроспективе видно, что в этих правилах нет ничего произвольного или выдуманного; они находятся в строгом соответствии с правилом Байеса. Настоящий вызов состоял в том, чтобы гарантировать удобное равновесие в конце — независимо от того, в каком порядке отправляются эти сообщения; более того, окончательное равновесие должно представлять «правильное» отражение веры в переменные. Под «правильным» я имею в виду такой же результат, как если бы мы проводили вычисления с помощью методов из учебника, а не путем передачи сообщений.

Это задача заняла меня и моих студентов, а также моих коллег на несколько лет. Но к концу 1980-х годов мы преуспели до такой степени, что байесовские сети стали практической схемой машинного обучения. За следующие 10 лет сфера их применения, например, для фильтрации спама и распознавания голоса, постоянно расширялась. Однако к тому времени я уже пытался подняться по Лестнице Причинности, передав вероятностную сторону байесовских сетей в другие надежные руки.