Если бы я был профессиональным историком, я бы остановился на этом месте. Но, поскольку я обещался быть историком-вигом, мне не удастся сдержать восхищения точностью слов Райта в цитате, приведенной в конце предыдущего раздела, которые не устарели за 90 лет с тех пор, как он высказал их впервые, и которые в основном и определили парадигму современного каузального анализа.

Мое восхищение точностью формулировки Райта уступает только восхищению его смелостью и целеустремленностью. Только представьте себе ситуацию, сложившуюся в 1921 году. Математик-самоучка в одиночку противостоит гегемонии всего статистического истеблишмента. Они говорят ему: «Ваш метод основан на полном непонимании природы причинности в научном смысле». Он стоит на своем: «Вовсе нет! Мой метод позволяет получать важные результаты и идет в этом дальше, чем все, что смогли придумать вы». Они говорят: «Наши великие гуру уже рассматривали эти вопросы 20 лет назад и решили, что то, что ты делаешь, лишено всякого смысла. Ты просто объединяешь корреляции с корреляциями и получаешь снова корреляции. Когда вырастешь — поймешь». А он продолжает: «Я не пытаюсь опровергнуть ваших гуру, но лопата — это лопата. Мои путевые коэффициенты — это не корреляции. Это нечто совершенно иное — это каузальные воздействия».

Представьте, что вы снова в детском саду и все дети над вами смеются, потому что вы считаете, что 3 + 4 = 7, в то время как любому ребенку известно, что 3 + 4 = 8. Вы идете к воспитательнице — а она тоже уверяет вас, что 3 + 4 = 8. Удалось бы вам не заплакать и не решить, что, наверное, это с вами что-то не то? В таких ситуациях даже самые сильные духом люди начинают сомневаться в истинности своих убеждений. Я сам был в таком детсаду, я знаю.

Но Райт не сдался. И это был не простой арифметический вопрос, в котором возможна независимая верификация. Ранее только философы осмеливались иметь собственное мнение о природе причинности. Откуда у Райта взялась эта внутренняя убежденность, что он на верном пути, а вся остальная группа детсада заблуждается? Может быть, то, что он вырос на Среднем Западе и учился в маленьком, никому не известном колледже, приучило его полагаться на собственные силы и дало понять, что самые надежные знания — это те, которые ты добываешь сам.

Одна из первых прочитанных мною в школе книг о науке рассказывала, как инквизиция заставила Галилея прилюдно отречься от учения о том, что Земля вращается вокруг Солнца, но после отречения тот упрямо прошептал: «И все-таки она вертится!» Вряд ли в мире есть ребенок, который, прочитав эту историю, не был вдохновлен смелостью и верностью Галилея своим убеждениям. Однако, как бы мы ни восхищались его позицией, сложно не думать о том, что он мог опираться по крайней мере на свои точные астрономические наблюдения. У Райта под рукой были только непроверенные выводы, например, что факторы внутриутробного развития отвечают за 58 %, а не за 3 % изменчивости окраски. Не имея ничего, на что можно было бы опереться, кроме внутреннего убеждения, что путевые коэффициенты способны рассказать нам то, чего не знают корреляции, он тем не менее объявил: «И все-таки она вертится!»

Коллеги говорят мне, что, когда истеблишмент в области искусственного интеллекта боролся с байесовскими сетями (см. главу 3), я действовал упрямо, самоуверенно и бескомпромиссно. В самом деле, я помню, что был совершенно уверен в верности своего подхода и не колебался ни на йоту. Но на моей стороне была теория вероятностей. Райт же не мог опереться даже на подходящую теорему. Ученые его времени отказались от причинности, поэтому никакого теоретического фундамента под свою работу он подвести не мог. Не мог он и опереться на авторитетные мнения, как тот же Найлз, потому что цитировать было некого: великие гуру вынесли свои окончательные вердикты еще десятилетиями ранее.

Однако у Райта было и утешение, был знак, что он на верном пути — понимание, что его метод дает ответы на вопросы, на которые нельзя ответить никак иначе. Одним из таких вопросов было определение относительной силы влияния нескольких факторов. Другой замечательный пример — в его статье «Корреляция и причинность» за 1921 год, где выясняется, как дополнительный день в утробе матери повлияет на вес новорожденной морской свинки. Ниже я разберу ответ Райта детально, чтобы показать красоту его метода и порадовать тех читателей, которые хотели бы видеть, как работает путевой анализ с математической стороны.

Обратим внимание, что мы не ответим на этот вопрос прямо, потому что не в силах взвесить морскую свинку еще в утробе. Мы, однако, способны сравнить вес при рождении у морских свинок, беременность матери которых длилась, скажем, 66 дней, с теми, которые провели в утробе 67 дней. Райт отметил, что, если беременность длилась на один день дольше, новорожденные свинки в среднем весили больше на 5,66 грамма. Можно наивно предположить, что за последний день в животе матери каждый детеныш морской свинки поправляется на эти 5,66 грамма.

«Неверно!» — говорит Райт. Детеныши обычно появляются на свет позже не просто так, а по определенной причине: в таких пометах обычно меньше детенышей. Это значит, что в течении всей беременности условия развития у них были лучше. Новорожденная морская свинка из помета, в котором было только трое детенышей, уже на 66-й день весит больше, чем из помета, в котором их было пятеро. Таким образом, разница в весе при рождении объясняется двумя разными причинами и нам надо их распутать. Сколько из дополнительных 5,66 грамма детеныш набирает за счет того, что проводит в матке на день больше, а сколько — за счет того, что у него меньше конкурентов?

Райт ответил на этот вопрос, начертив путевую диаграмму (рис. 12).

X — это вес детеныша при рождении. P и Q — два фактора, о которых известно, что они влияют на вес детеныша: P — продолжительность беременности, а Q — скорость роста в утробе матери. L — это число детенышей в помете, которое влияет сразу и на P, и на Q (при большом помете детеныши растут медленнее, а беременность длится меньше). Важно обратить внимание, что X, P и L можно измерить для каждого животного в отдельности, а Q — нельзя. Наконец, A и C — внешние причины, по которым у нас нет данных (т. е. наследственные и средовые факторы, влияющие на продолжительность беременности и скорость внутриутробного развития вне зависимости от числа детенышей в помете). Важное предположение, что эти факторы не зависят друг от друга, выражается отсутствием стрелки между ними, равно как и причины, влияющей на оба этих фактора.

Теперь можно сформулировать вопрос, стоявший перед Райтом: каково прямое влияние продолжительности беременности P на вес при рождении X? Данные (5,66 грамма за день) ничего не говорят нам о прямом влиянии — они дают нам только корреляцию, смещенную за счет влияния числа детенышей в помете L. Чтобы найти прямое влияние, мы должны устранить это смещение.

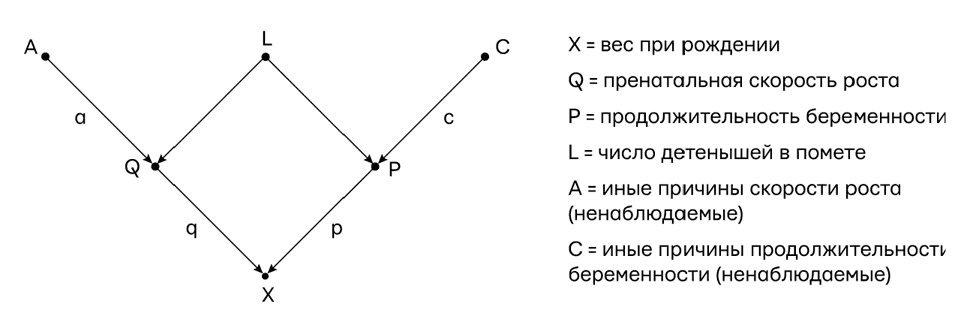
Рис. 12. Диаграмма причинности (путевая) для примера с весом при рождении

На рис. 12 прямое влияние обозначено путевым коэффициентом p, соответствующим пути P → X. Смещение за счет числа детенышей в помете соответствует пути P ← L → Q → X. А теперь в игру вступает магия алгебры: величина смещения равна произведению путевых коэффициентов вдоль по данному пути (иными словами, l умножить на l’ и умножить на q). Общая корреляция тогда равна просто сумме путевых коэффициентов по обоим путям: алгебраически p + (l ∙ l’ ∙ q) = 5,66 грамма в день. Если бы мы знали величину путевых коэффициентов q, l и l’, мы бы могли рассчитать второе слагаемое и вычесть его из 5,66, получив p. Но мы их не знаем, потому что Q, например, невозможно измерить. Но именно здесь и проявляется гениальность метода путевых коэффициентов. Метод Райта расписывает, как выразить каждую из посчитанных корреляций в соответствующих терминах. Сделав это для каждой из измеренных пар (P, X), (L, X) и (L, P), мы получаем три уравнения, которые решаются алгебраически для неизвестных путевых коэффициентов, p, l’ и (l ∙ q). После этого задача решена, желаемая величина p найдена.

Сегодня мы можем обойтись вообще без математики и рассчитываем p посредством беглого изучения диаграммы. Но в 1920 году это был первый случай, когда математику призвали объединить корреляции и причинность. И это сработало! Райт вычислил, что p равно 3,34 грамма в день. Другими словами, если все другие переменные (A, C, L, Q) остаются постоянными и только срок беременности увеличится на один день, средний рост веса при рождении составит 3,34 грамма. Заметим, что этот результат имеет внятный биологический смысл. Он говорит нам, с какой скоростью детеныши растут в каждый день внутриутробного развития. Число 5,66, напротив, биологически бессмысленно, потому что оно смешивает два разных процесса, один из которых не каузальный, а антикаузальный (или диагностический): это связь P ← L.

Приведенный пример преподает нам два урока. Первый: причинный анализ позволяет нам находить численные выражения реальных процессов в реальном мире, а не только структуры данных. Детеныши растут со скоростью 3,34 грамма в день, а не 5,66 грамма в день. Урок второй: следили вы за математикой или нет, но в путевом анализе мы делаем выводы об индивидуальных причинно-следственных отношениях, изучая диаграмму в целом. Чтобы оценить каждый индивидуальный параметр, может понадобиться структура всей диаграммы.

В воображаемом мире, где наука развивается логично, ответ Райта Найлзу должен был бы вызвать всеобщий научный восторг, а затем его методы с энтузиазмом стали бы применять другие ученые и статистики. Но судьба распорядилась иначе. «Одна из загадок истории науки в период с 1920 по 1960 годы — это практически полное отсутствие применения путевого анализа, за исключением самого Райта и селекционеров животных, — писал один из коллег Райта генетик Джеймс Кроу. — Хотя Райт продемонстрировал много примеров возможного применения своего метода, ни по одному из предложенных им путей никто не пошел».

Кроу не знал об этом, но такое загадочное умолчание коснулось и общественных наук. В 1972 году экономист Артур Гольдбергер оплакивал «постыдную неизвестность» работ Райта в тот период и отмечал, с энтузиазмом новообращенного, что «подход [Райта] стал искрой, воспламенившей нынешний интерес к каузальным моделям в социологии. Ах, если бы мы могли обратиться к современникам Райта и спросить — почему вы не обратили внимания? Кроу дает такой ответ: „путевой анализ не годится для программ-„консервов”. Пользователь должен самостоятельно сформировать гипотезу и создать годную диаграмму из множества причинных последовательностей”». Действительно, Кроу указал на важный момент: путевой анализ, как и любое упражнение в области причинно-следственных связей требует умения научно мыслить. Статистика же, как это часто случается, не поощряет его, способствуя появлению программ-«консервов», применяемых механически. Ученые всегда будут предпочитать рутинные вычисления на основе данных методам, которые бросают вызов их научным познаниям.

Рональд Эйлмер Фишер, непререкаемый авторитет в области статистики в поколении после Гальтона и Пирсона, характеризует эту разницу лаконично. В 1925 году он пишет: «Статистику можно назвать… наукой о методах редукции данных». Обратите внимание на слова «методы», «редукция» и «данные». Райту претило представление о статистике как только о собрании методов — Фишеру оно было по душе. Причинно-следственный анализ, подчеркнем, не сводится к данным: в ход анализа мы должны инкорпорировать некоторые представления о процессах, которые приводят к появлению этих данных, и тогда мы получаем в результате нечто, что исходно в наших данных не содержалось.

Но в одном Фишер был прав: если убрать из статистики причинность, редукция данных — это все, что вам остается.

Хотя Кроу и не упоминает этого, биограф Райта Уильям Провин указывает еще на один фактор, который мог повлиять на недостаток поддержки путевого анализа. С середины 30-х годов ХХ века Фишер считал Райта своим врагом. Я ранее цитировал воспоминания Юла о том, как отношения с Пирсоном резко становились натянутыми, если кто-то не соглашался с ним, и невозможными — если Пирсона критиковали. Совершенно то же самое справедливо и в отношении Фишера. Последний устраивал продолжительные вендетты всем, с кем был не согласен, включая Пирсона, его сына Эгона, Ежи Неймана (о них обоих будет подробнее в главе 8) и, конечно, Райта.

Главной точкой соперничества Фишера и Райта был не путевой анализ, а эволюционная биология. Фишер был не согласен с теорией Райта (называемой генетическим дрейфом), согласно которой вид может эволюционировать очень быстро, когда проходит через популяционное бутылочное горлышко. Детали этого спора выходят за рамки данной книги, и заинтересованный читатель должен обратиться к работе Провина. Важно здесь, однако, следующее: с 20-х до 60-х годов ХХ века научный мир был преимущественно повернут лицом к Фишеру, как к оракулу статистических знаний. И уверяю вас, что он никогда не сказал ни одного доброго слова про путевой анализ.

В 1960-х все стало понемногу меняться. Группа представителей общественных наук, включающая Отиса Дункана, Хьюберта Блалока и экономиста Артура Гольдбергера (упомянутого ранее), заново открыла путевой анализ как метод предсказания результатов социальной и образовательной политики. По иронии судьбы Райта приглашали выступить перед влиятельной группой эконометриков, комиссией Каулза, в 1947 году, но ему совершенно не удалось разъяснить им, в чем смысл путевых диаграмм. Только когда экономисты сами додумались до подобных идей, на короткое время удалось установить контакт. Судьба путевого анализа в экономике и в социологии двигалась по разным траекториям, но каждая из них вела к предательству идей Райта. Социологи переименовали путевой анализ в уравнения структурного моделирования (Structural Equation Modeling; SEM), полюбили диаграммы и активно их использовали до 70-х годов прошлого века, когда компьютерная программа LISREL автоматизировала подсчет путевых коэффициентов (в некоторых случаях). Райт мог бы предсказать то, к чему это привело: путевой анализ превратился в рутинный метод, а исследователи стали пользователями программы, которых слабо интересует, что у нее внутри. В конце 1980-х обращенный к научному обществу призыв (статистика Дэвида Фридмана) объяснить допущения, стоящие за уравнениями структурного моделирования, был проигнорирован, а некоторые эксперты по SEM даже отрицали, что этот метод как-то связан с причинностью.

В экономике алгебраическая часть путевого анализа получила известность как системы одновременных уравнений (без общепринятого сокращения). Экономисты почти никогда не использовали путевые диаграммы и продолжают обходиться без них и по сей день, полагаясь взамен на числовые уравнения и матричную алгебру. Прямое последствие этого подхода в том, что, поскольку алгебраические равенства не направлены(т. е. x = y — это то же самое, что и y = x), у экономистов не было обозначений для различения причинных и регрессионных уравнений, поэтому на вопросы, связанные с выбором стратегии, не получалось ответить даже после того, как уравнения были решены. Вплоть до 1995 года большинство экономистов избегали прямо придавать своим уравнениям каузальный или контрфактивный смысл. Даже те из них, кто использовал структурные уравнения для обоснования выбора стратегических решений, неизлечимо боялись диаграмм, хотя те могли бы избавить их от многих страниц лишних вычислений. Неудивительно, что многие экономисты и сегодня стоят на точке зрения «в данных уже содержится все».

По всем этим причинам многообещающие перспективы путевых диаграмм оставались реализованы только отчасти, по крайней мере до 90-х годов прошлого века. В 1983 году Райта снова лично вызвали на ринг защищать их, на этот раз в «Американском журнале генетики человека». В то время, когда он писал эту статью, ему уже было за 90. Читать его эссе 1983 года одновременно и радостно, и больно — оно о том же, о чем он писал в 1923 году. Много ли в истории науки случаев, когда нам выпадала честь вновь выслушать создателя великой теории через 60 лет после того, как он впервые изложил ее на бумаге? Это примерно как если бы Чарлз Дарвин восстал из могилы, чтобы поприсутствовать на «обезьяньем процессе» Скоупса в 1925 году. Но это и трагично, потому что за эти 60 лет теория должна была расти, развиваться, цвести, а вместо этого она осталась практически на том же уровне, что и в 1920-х.

Написать статью Райта побудила критика путевого анализа, которую ранее опубликовали в том же журнале Самуэль Карлин (математик Стэнфордского университета, награжденный в 1989 году Национальной научной медалью, внесший фундаментальный вклад в экономику и популяционную генетику) и два его соавтора. Нас здесь интересуют два аргумента Карлина.

Во-первых, путевой анализ вызывает у Карлина возражения по причине, которую Найлз не упомянул: он предполагает, что все взаимоотношения между любыми переменными в путевой диаграмме линейны. Это допущение позволило Райту описать каузальные взаимодействия с помощью только одного числа — путевого коэффициента. Если бы уравнения были нелинейны, то тогда воздействие на Y от изменения X на единицу зависело бы от текущего значения X. Ни Карлин, ни Райт не знали, что до появления общей теории нелинейности осталось совсем немного (ее всего три года спустя разработает звезда моей лаборатории Томас Верма).

Но самое интересное возражение Карлина — как раз то, которое он считал важнейшим: «Наконец, с наибольшим успехом исследователь может выбрать подход, не предполагающий модели вообще, приводящий к пониманию данных интерактивно, используя ряд отображений, индексов и контрастов. Этот подход подчеркивает концепцию надежности данных в интерпретации результатов». В одном этом коротком отрывке Карлин выражает, сколь мало изменилось со времен Пирсона и насколько влиятельной его идеология оставалась даже в 1983 году. Он говорит, что в самих данных уже заключена вся научная мудрость; их нужно только уметь умаслить и сделать им массаж (с помощью отображений, индексов и противопоставлений), и они сами выронят жемчуг мудрости вам в руки. Нашим аналитикам нет нужды принимать во внимание процессы, которые привели к появлению этих данных. У нас все получится ровно так же, и даже лучше с подходом, «не предполагающим никакой модели вообще». Если бы Пирсон жил сегодня, в эпоху больших данных, он сказал бы ровно это: все ответы уже содержатся в самих данных. Конечно, утверждения Карлина нарушают все, о чем мы говорили в первой главе. Чтобы говорить о причинности, нам требуется ментальная модель реального мира. «Безмодельный подход» может привести нас на первую ступень Лестницы Причинности, но никак не дальше.

Райт, надо отдать ему должное, прекрасно понимал, как велики ставки, и написал недвусмысленно: «Заявляя, что подход, не предполагающий модели вообще — наилучшая альтернатива… Карлин с соавторами хотят не просто изменить метод путевого анализа, но лишить его цели и оценки относительной важности различных причин. Этот анализ невозможен без модели. Они предлагают тем, кому хочется провести такую оценку, подавить свое желание и заняться чем-нибудь другим».

Райт понимал, что защищает саму суть научного подхода и интерпретации данных. Сегодня я бы дал энтузиастам больших данных, избегающим моделей, тот же совет. Конечно, замечательно попытаться выудить всю информацию, которую данные способны нам сообщить, но надо понимать, насколько далеко это позволит нам уйти. А уйти оно позволит не дальше первой ступени Лестницы Причинности и никогда не сможет дать ответ даже на такой простой вопрос: какова относительная важность различных действующих факторов?

E pur si muove!