Божественные машины

Шел 1943 год. Беседа между двумя джентльменами, регулярно встречавшимися за чаем в кафетерии при Лаборатории Белла, текла довольно вяло. Долговязый американец был вполне открыт для светской беседы, его интересовало множество вещей, например джаз, езда на велосипеде, жонглирование и машины, способные читать мысли, его собеседник, англичанин, оказался замкнутым и нелюдимым и охотно называл себя отшельником. Они не могли говорить о своих исследованиях: они оба работали над проблемами шифрования, и им запрещалось распространять информацию об этом за пределами своего отдела. Поэтому они увлеченно играли в интеллектуальную игрой: будут ли компьютеры в ближайшем будущем обладать сознанием и смогут ли они думать, как люди, и если да, то как это можно проверить? В один из редких эмоциональных моментов во время беседы в кафетерии англичанин, Алан Тьюринг, воскликнул, что он хотел бы создать не гениальный мозг, а совершенно нормальный мозг, такой, как у президента AT&T, компании, которая в то время владела Лабораториями.

Оба собеседника принадлежали к числу самых блистательных умов своего времени. Американец Клод Шеннон занимался разработкой математически фундированной теории информации, основанной на проблеме шифрования, а Тьюринг недавно разгадал код немецкой шифровальной машины «Энигма» и тем самым оказал заметное влияние на ход войны.

Тьюринг уже создал «мыслящую машину», правда, только в своей голове. Эта машина состояла из хранилища для программ и данных, головки для чтения и записи и бесконечно длинной полосы бумаги. Ей было суждено внести вклад в решение вопроса о том, могут ли машины мыслить. Сам Тьюринг в 1936 году, когда вышла его статья «О вычислимых числах», сформулировал эту проблему более осторожно: можно ли вычислить все? За этим стоял вопрос, могут ли машины принимать решения, что, по мнению Тьюринга, означало бы, что они мыслят.

Тьюринг доказал с помощью виртуальной машины, более известной как Универсальная машина Тьюринга, что это невозможно. Так он отреагировал на проблему разрешения, сформулированную геттингенским математиком Давидом Гильбертом. Гильберт хотел знать, может ли математика быть полной, то есть возможно ли решить все математические задачи с помощью фиксированной процедуры, без человеческой интуиции или гениальных идей. В этом случае их могла бы решить и машина. Тьюринг создал такую машину в своем воображении и использовал ее, чтобы доказать, что даже его бесконечная машина с бесконечно длинной полоской бумаги не может вычислить все числа. Это нанесло тяжелый удар программе Гильберта, после чего она была окончательно опровергнута Куртом Гёделем, но это уже другая история.

В наши задачи не входит описание деталей этой дискуссии о полноте математики. Важно лишь то, насколько тесно разработка компьютера была связана с вопросом об антропологических различиях. Для чего бы ни предназначались компьютеры – для оптимизации противовоздушной обороны, создания атомной бомбы, для предсказания погоды или биржевых спекуляций, – вопрос о том, что такое человек, оказывается существенным с самого начала. Точнее, на кону стояло нечто большее. Тьюринг хотел создать не просто мыслящую машину, как он объявил тогда в кафетерии, а совершенную машину, которая могла бы рассчитать все и решить все проблемы.

Тьюринг искал божественную машину.

Тем временем он вернулся в Англию. Вопрос о том, может ли машина мыслить, как человек, и обретут ли компьютеры когда-нибудь сознание, не оставлял его. Позднее его судили за гомосексуальность и заставили пройти химическую кастрацию, после чего Алан Тьюринг, один из самых значительных ученых XX века, покончил с собой.

Тьюринг предложил тест, который, по его собственной осторожной формулировке, поможет выяснить, сумеет ли человек определить, с кем он общается – с другим человеком или с машиной. Этот тест известен как тест Тьюринга, хотя сам ученый называл его игрой в имитацию, поскольку речь шла о том, может ли компьютер подражать человеку.

Тьюринг несколько раз менял схему теста, но принцип оставался прежним: испытуемый А сидит напротив человека В и машины С за занавеской. А разрешается задавать В и С столько вопросов, сколько он хочет, в письменном виде, а в конце он должен определить, кто из них двоих человек, а кто машина. Конечно, В и С могут лгать.

«Бомба» Тьюринга – Уэлчмена – компьютер, который Тьюринг сконструировал в Блетчли-Парке специально для расшифровки сообщений, закодированных немецкой шифровальной машиной «Энигма»

Без сомнения, компьютер изначально задумывался как полезная машина – если в войне вообще можно найти нечто полезное, – но одержимость вопросом о том, может ли машина обладать сознанием и мыслить, сохраняющаяся по сей день, наводит на мысль, что за этим кроется нечто большее. Похоже, наше понимание самих себя зависит от странного вопроса о том, чем мы по существу отличаемся от машины, в противном случае можно с уверенностью предположить, что, даже если компьютер обладает сознанием и может мыслить, он не может прогуляться по лесу, насладиться сексом или приготовить идеальный томатный соус – и все это за одно воскресенье.

Фильм «Бегущий по лезвию» Ридли Скотта (1982) дает представление о том, что такое тест Тьюринга. Разновидность этого теста появляется в фильме под названием теста Войта – Кампфа. С помощью щелевой лампы, подобной тем, что используют офтальмологи, полицейский, который занимается поиском андроидов, незаконно находящихся на Земле, проверяет реакцию зрачков испытуемых на стрессовые вопросы. Теоретически, в отличие от человека, машина не должна проявлять никаких эмоциональных реакций. Однако уже на первом тесте ситуация выходит из-под контроля. Когда руководитель эксперимента спрашивает андроида о его матери, он приходит в такую ярость, что стреляет в экспериментатора.

В этой мрачной антиутопии также поднимается вопрос о том, как отличить машины от людей. В фильме, словно в затянувшемся тесте Тьюринга, перебираются один за другим все возможные отличительные признаки. Эмоции, как мы видели, не являются надежным критерием различия. Что же тогда – интеллект, любовь, душа (которая отражается в глазах), воспоминания? В заключительном монологе андроид Рой Бэтти (Рутгер Хауэр) дает тревожный ответ: истинно человеческим является осознание собственной конечности – в фильме этого достигает только машина, тогда как человек боится признать это.

«Бегущий по лезвию» затрагивает суть игры в имитацию. Кто кому подражает на самом деле? Тьюринг хотел лишь выяснить, могут ли компьютеры имитировать людей или человеческое сознание. Он не учитывал, что испытуемый может быть обманут тем, что за ширмой человек ведет себя как компьютер, по крайней мере в первой версии теста. Однако это был бы вполне закономерный, если не сказать более – животрепещущий вопрос: может ли человек мыслить как компьютер? Или мы уже мыслим как компьютеры? И что это значит?

Давайте мысленно перевернем тест Тьюринга и спросим, может ли человек настолько точно имитировать компьютер, что их уже невозможно будет отличить друг от друга.

Для начала проясним вопрос о том, как машины думают. Идея уступить мышление машине гораздо старше Тьюринга и Шеннона. Алан Тьюринг был далеко не первым, кто построил машину в своей голове, или, выражаясь более элегантно, сконструировал символическую машину.

Примерно за семь веков до него каталонский дворянин Раймунд Луллий (ок. 1232–1316 гг.) попытался создать мыслящую машину, причем, как это ни удивительно, руководствуясь примерно теми же мотивами, что и Тьюринг: он хотел построить машину, которая могла бы производить универсальные истины, не зависящие от ограниченного разума человека.

После серьезного разочарования в любви бонвиван удалился в горы, чтобы отныне полностью посвятить свою жизнь Иисусу Христу. В созерцании распятого Христа ему открылась его личная миссия: он должен проповедовать Евангелие неверующим! Но он не знал, как это сделать, так как не видел причин, почему неверующие должны следовать Евангелию, если у них есть собственная богатая традиция. Он понимал, что одна лишь Благая Весть никого не убедит. Ему нужны были аргументы, не зависящие от культуры, универсальные и объективно истинные; другими словами, ему нужна была мыслительная машина типа счетной машины или абакуса, потому что только машины абсолютно надежны, объективны, универсальны – и настолько эффектны, что могут убедить каждого.

Поэтому Луллий взялся за создание машины, которая могла бы самостоятельно связывать понятия по определенным правилам так, чтобы в итоге получались объективно истинные утверждения, подобно тому как счетные машины самостоятельно связывают числа по определенным правилам. Машина Луллия не осталась в его воображении. В некоторых изданиях его главного труда «Всеобщее и последнее искусство», для краткости называемого «Великим искусством», который вышел в свет только в 1306 году, мы находим устройство, похожее на парковочный диск и состоящее из множества дисков, вращающихся вокруг центра. Каждый из этих дисков разделен на сектора, в которых написаны названия различных категорий или обозначающие их буквы. Категории – это, например, проявления Бога, логические операции, качества, отношения, сотворенные вещи и так далее. При вращении дисков образуются связи, которые, согласно идее Луллия, образуют новые, объективно истинные предложения. Раймунд Луллий создал первую логическую машину, которая, в отличие от счетных машин, выдавала не число, а истинное предложение. Однако для распространения христианства она, видимо, оказалась малопригодна: Луллий умер в возрасте 83 лет от побоев, полученных им во время демонстрации жителям Северной Африки истин, которые произвела его машина.

В отношении получаемых таким путем «истин» машину Раймонда Луллия следует поставить в один ряд с непонятными магическими практиками и каббалистической мистикой чисел, под влиянием которой он находился. Однако – и за это ему следует отдать должное – он был первым, кто задумался о том, что машина может мыслить. Технически машина Луллия имеет мало общего с современным компьютером, за исключением того, что она использует булеву логику, но об этом позже.

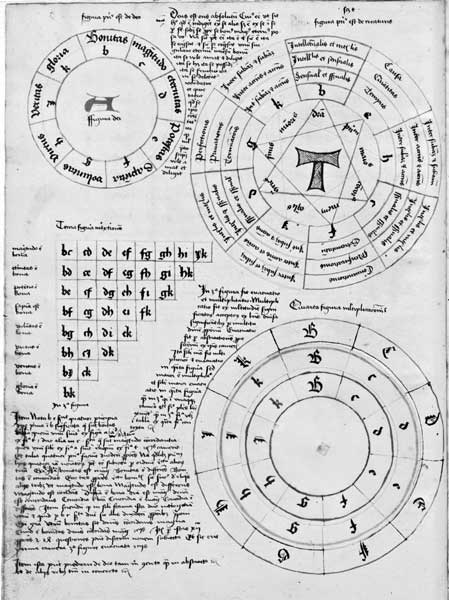
Четыре фигуры «Малое искусство» (Ars brevis)

Хотя машина Луллия, вероятно, не смогла убедить ни одного неверующего, она, по крайней мере, разоблачила фантазии, которые были движущей силой создания мыслящих машин в будущем. То, что компьютер быстро и надежно обрабатывает огромные объемы данных, – это лишь практическая сторона медали. Для Луллия и Тьюринга не менее важен поиск универсальности, объективности и совершенства. По их убеждению, достичь этого возможно только с помощью механизированного мышления, поскольку только машины гарантируют независимость от эмоций, властных отношений и индивидуальных склонностей. И когда в наши дни в гимназиях и университетах, а также на рынке труда обсуждается введение вступительных испытаний, основанных на компьютерном тестировании интеллекта, это показывает, что мечта о механическом, универсальном и объективном мышлении, не отравленном никакими частными интересами, не изжита даже спустя почти восемь веков после Луллия.

Готфрид Вильгельм Лейбниц, о котором мы уже говорили в связи с его планом создания кунсткамеры, также разработал проект виртуальной мыслящей машины. В своей ранней работе «О комбинаторном искусстве» он расширил идею Луллия о комбинаторике: мыслить означает комбинировать все со всем по правилам.

Лейбниц не был одаренным механиком. Из пяти вариантов сконструированной им счетной машины ни один не работал, равно как и его часы с двумя балансами. Его гениальная догадка использовать энергию ветра в шахтах провалилась, потому что он не учел, что ветер дует не всегда. Вместе с тем идеи, лежащие в основе этих изобретений, были поистине новаторскими. Его комбинаторика, позже формализованная Джорджем Булем, стала незаменимым подспорьем для развития компьютера.

По задумке Лейбница, виртуальная машина должна создать язык, в котором путем комбинирования генерируются истинные предложения: он не только выражает все существующие факты, но и порождает новые – это ars inveniendi, искусство отыскания. Лейбниц считал, что обычные языки не могут адекватно выражать разум. Множество языков само по себе доказывает, что они не в состоянии правильно выразить единственный разум. Как прекрасно было бы иметь знание, свободное от ложного словоупотребления, то есть язык, действительно соответствующий универсальной и единой науке, слова которого просты, ясны и систематически упорядочены.

Из кратких записей Лейбница сложно понять, что именно он собирался предпринять для достижения этой цели. Ясно лишь, что он хотел разложить все известные знания на простые идеи, присвоить им номера, а затем комбинировать и вычислять с их помощью.

Лейбниц справедливо не был удовлетворен своими попытками: все они оказались тупиковыми. То, что трактат о комбинаторном искусстве был переиздан в 1790 году без его ведома, раздражало его; он предпочел бы, чтобы об этой работе забыли навсегда. Трудно судить о том, что в итоге помешало гениальному ученому. Кто-то скажет, что любая попытка создать идеальный язык обречена на неудачу. На это можно возразить, что языки программирования в значительной степени отвечают требованиям, которые Лейбниц предъявлял к универсальному языку. В любом случае все элементы, необходимые для изобретения формального универсального языка, – двоичная логика, исчисление бесконечно малых как алгоритмическая процедура и конкретная вычислительная машина, которая дает представление о том, как можно решать механические проблемы, – уже были найдены им. Едва ли здесь могло помешать то, что в то время еще не существовало электричества: вычислительная машина Чарльза Бэббиджа тоже работала чисто механически.

Возможно, Лейбниц потерпел неудачу, так как не понимал, что универсальный идеальный язык уже существует – это математика. Все, что ему нужно было сделать, это объединить математику чисел и логику языка.

Этот последний и решающий шаг сделал Джордж Буль (1815–1864) через шесть веков после Луллия и через два после Лейбница: он объединил язык с математикой, логику с алгеброй. Буль был самоучкой, не получившим никакого формального образования, кроме начальной школы. Кое-что он узнал от отца-сапожника, а кое-что, главным образом латынь, – от друга-букиниста. Остальное и, судя по всему, основное, он изучил сам, причем так, что смог стать профессором математики в Королевском колледже в Корке. Однажды, возвращаясь после лекции, он сильно промок под дождем. Когда он пришел домой, его жена, увлекавшаяся гомеопатией, сторонница лечения подобного подобным, облила его холодной водой, от чего он заболел пневмонией и умер. Эта смерть бросает небольшую тень на проект всей его жизни – подчинить мышление математической строгости.

Его главный интерес – исследование законов мышления: именно так называется его главная работа в немецком переводе. Вдохновленный логикой Аристотеля, он решил перевести описанные в ней законы мышления в математическую форму: «Какими бы ни были по своей сути те универсальные законы, которые составляют основу всякого мышления, по крайней мере по своей форме они являются математическими».

Буль исходил из следующих соображений: так же, как все числа можно связывать друг с другом только двумя операциями – сложением и умножением, предложения должны соединяться несколькими логическими операциями. Но, в отличие от алгебры, в логике возможны только два результата – истина или ложь. Истине присваивается значение 1, лжи – значение 0. С помощью логических операторов, которые мы и сегодня используем в поисковых системах, – AND [Λ], OR (V), NOT (¬), – все пропозициональные предложения, то есть все предложения, которые вообще могут быть истинными, соединяются друг с другом и проверяются на истинность.

Так Булю удалось объединить алгебру и логику: все связи высказываний теперь можно было формализовать так, что машина могла проверить их истинность. Буль не создал собственную мыслящую машину, но его логическая алгебра положена в основу всех мыслящих машин.

В 1950 году Клод Шеннон сконструировал электрическую мышь и назвал свое изобретение «Тесей», потому что она, подобно Тесею из античных мифов, самостоятельно перемещалась по лабиринту. Более того, она запоминала однажды пройденный путь и училась заново, если лабиринт менялся. Конечно, в то время мышь была слишком мала для компьютера. На самом деле машина находилась под полом лабиринта: Шеннон собрал ее дома из нескольких старых телефонных реле, используя булеву логику. Тем самым Шеннон осуществил свою старую задумку. В 1938 году, еще до работы в лабораториях Белла, он окончил Массачусетский технологический институт, защитив магистерскую диссертацию «Символический анализ релейных и коммутационных цепей», в которой он теоретически показал, что булева логика может быть применена к электронным схемам. Позднее эту работу назовут одной из самых важных магистерских диссертаций века. С помощью «Тесея» он смог практически обосновать свою идею и представить ее непрофессиональной аудитории.

Эпохальное достижение Буля поставило крест на идее универсального языка, независимого от математики. Тем временем философы Готтлоб Фреге, Бертран Рассел и молодой Витгенштейн пришли к мысли, что математика должна быть основой формальной логики. Однако они видели, что для этого требуется новое понимание математики. Чтобы механизировать ее, необходимо, подобно Лейбницу и Луллию, представлять мышление как комбинаторное искусство, искусство установления связей, а не как искусство доказательства. Речь идет об отношениях между числами или понятиями и предложениями, а значит, о процессах, но не об определениях.

Это означает, что математику нужно понимать как набор правил для процедур и преобразований – в противовес европейской традиции со времен Пифагора (570–510 гг. до н. э.), которая видела в ней всеобщую и вместе с тем наивысшую из всех форм знания, истинную всегда, везде и для всех и поэтому призванную служить познанию конечных вещей, не касаясь области профанных расчетов.

Это идеализированное представление о математике живо и по сей день. Сегодня всех студентов-математиков в первом семестре учат, что красивое доказательство – это высшая форма математики. Их соседи, студенты, изучающие информатику, смеются над этим, потому что для них важно разработать вычислительные методы, которые были бы максимально быстрыми и полезными. Нужны хорошие алгоритмы.

Но что такое алгоритм? Изначально простой алгоритм – это не что иное, как правило преобразования: так, x = y² – алгоритм, который дает команду присвоить каждому y значение x, равное y, умноженному на y. Графически это можно представить в виде параболы с вершиной (0/0) или в виде списка: 0/0, 1/1, 2/4, 3/9, 4/16 и так далее.

Обычно такое простое правило называют не алгоритмом, а функцией. Об алгоритмах в более узком смысле говорят только тогда, когда функции последовательно связаны, то есть когда результат функции a становится исходным значением функции b и возникают ветвления и циклы. При ветвлении условие определяет, какая функция вычисляется следующей и по какому пути должен идти алгоритм. Например, инструкция может иметь следующий вид: если результатом вычисления является m ≥ x, вычислить функцию n, если m < x, вычислить функцию p. Если в условии указано, что результат функции «возвращается» в ту же функцию, то это называется циклом. В точке ветвления принимается решение, основанное, правда, не на общем принципе, а лишь на последнем результате. Можно сказать, что алгоритм – это серия решений.

Этот вид арифметики, вероятно, «изобрели» крупные землевладельцы Кералы. Астрономические расчеты были необходимы для управления обширными землями в этом муссонном регионе, но управление и обмеры также требовали удобных и простых в использовании арифметических процедур. «Арьябхатия» – один из самых важных текстов индийской математики, сравнимый с «Элементами» Евклида, датируемый примерно V веком, – содержит 121 геометрический и алгебраический метод вычислений: все они применялись в астрономии, управлении или геодезии. Читателей, знакомых с европейской традицией, удивит то, что во всем тексте не встречается ни одного доказательства. Примечательно, что эти методы вычислений зачастую основывались на приближениях, достаточных для повседневного использования.

Мухаммад ибн Муса аль-Хорезми, персидский ученый, живший в Багдаде в IX веке и зарабатывавший на жизнь будучи главным библиотекарем, решил сделать индийскую математику доступной для арабского мира и написал компендиум «Аль-Джабр» (от этого слова происходит термин «алгебра»), получивший широкое распространение в Европе. Имя аль-Хорезми, труднопроизносимое для европейцев, в процессе перевода заменено на Algorizmi или Algorizmus, алгоритм.

Так в Европе появилась вторая математика, которую, в противоположность традиционной греческой математике, интересовали не доказательства, а только подходящие методы вычисления. Эти методы, в том числе, например, исчисление бесконечно малых, обычно состояли из серии вычислений, а потому, в отличие от математики доказательств, были механизируемы.

Лучше всех суть алгоритмического мышления выразил Лейбниц: «Естественные изменения монад исходят из внутреннего принципа, так как внешняя причина не может иметь влияния внутри монады». Это означает, что решения принимаются по внутренним причинам, а не на основе внешних принципов. Представим себе двух туристов в горах. Неопытный ориентируется по официальной, общедоступной карте; он легко заблудится, потому что карта отображает только общее и неизменное положение дел, а не текущие условия. Опытный турист, напротив, никогда не полагается только на карту: принимая решение о продолжении похода, он учитывает маркировку тропы, рельеф местности, погоду, свое снаряжение, уровень подготовки и время, оставшееся до наступления сумерек. Все эти данные, доступные в настоящий момент, создают картину, которая позволяет ему сделать четкий прогноз. Такие вводные данные, как «темные облака», «устал», «крутой рельеф», «четыре часа дня», подскажут одно решение, при других начальных условиях – «ясное небо», «хорошо подготовлен», «ровная местность», «десять часов утра» – выбор будет иным. Серийное мышление определяет будущее на основе прошлого, поэтому машина обладает способностью к предвидению.

Соответственно, компьютер должен уметь принимать решения, как наш турист. Для этого недостаточно, чтобы программа последовательно выполняла одну команду за другой. Только условные инструкции (если идет дождь, то ехать на поезде, в ином случае идти пешком) приближают компьютер к метамашине, которую искал Тьюринг, – машине, которая может управлять любой другой машиной.

Ни одна из мыслящих машин, с которыми мы до сих пор сталкивались, не была способна на это. Они были такими же умными, как парикмахеры. Это ни в коем случае не уничижение профессии, а исторический факт. Ведь после Французской революции большинство парикмахеров лишились средств к существованию. Сложные прически и парики старого режима вышли из моды, и те, кто продолжал их носить, рисковали потерять не только волосы. Спад интереса к аристократическим прическам совпал с появлением таблиц чисел. В рамках десятичной системы, введенной в годы революции, потребовалось пересмотреть логарифмические таблицы, астрономические таблицы (для навигации) и ожидаемую продолжительность жизни (для страхования) и свести их в единые таблицы.

После прочтения знаменитой главы о разделении труда в «Богатстве народов» Адама Смита у директора парижского кадастрового бюро Гаспара де Прони (1755–1839) случился приступ вдохновения. Почему бы не поручить безработным парикмахерам произведение необходимых расчетов с разделением труда, аналогично тому, как рабочие в книге Смита делают булавки? Любой человек будет выполнять вычисления так же хорошо, как математик, если он работает в команде и должен освоить только одну вычислительную операцию. Фактически де Прони начал нанимать парикмахеров в свой офис, называя их компьютерами, потому что они целыми днями только и делали, что вычисляли.

Тем не менее ошибки случались, и даже слишком часто. Это понял английский математик Чарльз Бэббидж. То, что могут делать парикмахеры, машины сумеют сделать быстрее и безошибочнее, подумал он и решил построить вычислительную машину, которая умела бы заполнять таблицы. В последующие годы он тратил все свое время, энергию и огромные суммы своих и чужих денег на разработку разностной машины. Почему она так и не заработала – вопрос спорный. Может быть, работавшие у него инженеры были недостаточно хороши? У него закончились деньги? Или продолжать работу было невозможно из-за его ссоры с главным механиком Джозефом Клементом? Может быть, он поссорился с покровителями из-за своего вспыльчивого характера? Или он просто потерял интерес к делу, когда ему пришла в голову идея аналитической машины?

Чарльз Бэббидж. Разностная машина № 1

Как бы то ни было, разностная машина, если бы она когда-нибудь заработала, умела бы решать только одну задачу, для которой она создавалась, – заполнение таблиц. Аналитическая машина, напротив, могла бы адаптироваться к поставленной задаче, как хамелеон, или лучше – как человеческий разум. Но это означало, что она должна быть программируемой. Бэббидж представлял себе перфокарты, знакомые ему по ткацкому станку Жаккарда. В конце концов, разница невелика: вместо того, чтобы ткать узоры, задача теперь состояла в том, чтобы обрабатывать мыслительные схемы.

Но аналитическая машина так и осталась незавершенным проектом. На первую вычислительную машину ушло столько денег, что не нашлось спонсоров для гораздо более дорогой программируемой машины; к тому же Бэббидж не был склонен к заискиванию перед потенциальными покровителями. Сохранившиеся планы подготовлены не самим Бэббиджем, а (согласно отчетам) итальянским математиком Федерико Луиджи Менабреа – еще до того, как он стал премьер-министром Пьемонта.

Чего хотел Бэббидж от своих машин? Польза от разностной машины заключалась в том, что она умела самостоятельно заполнять таблицы, но для аналитической машины Бэббидж поначалу не мог придумать никакого практического применения, за исключением того, что она, вероятно, научилась бы играть в шахматы. С помощью аналитической машины он рассчитывал достичь большего: подобно тому как тепловой двигатель отделил труд от человека и сделал его независимым, аналитическая машина должна была сделать интеллект самостоятельной, измеряемой величиной, отдельной от человека.

Цепочка операций – это не только новый математический принцип, но и основа индустриализации, зарождавшейся во времена Бэббиджа. В доиндустриальную эпоху, согласно Марксу, стоимость создавалась ремесленником, который производил изделие с помощью своего инструмента. Фабрика отделила инструмент от человека. Отныне машина принадлежала не тому, кто ею управлял, а тому, кто за нее платил. Производство изделия теперь находилось не в руках одного ремесленника, а распределялось между различными участниками производственной цепочки – машинами или людьми. Разделение труда распространилось и на машины, а человек оказался низведенным до орудия, находящегося на одном уровне с машинами. Действия, требовавшие максимум силы и минимум интеллекта, выполняли машины, остальные – люди.

Бэббидж делает еще один шаг, имевший огромные последствия. Когда модель разделения труда Адама Смита была распространена на машины, учитывалась только физическая сторона производства, затраты сил и энергии. Теперь же с помощью своей аналитической машины Бэббидж нашел возможность включить в эту модель умственный труд – планирование, управление, контроль и т. д. Для этого он отделил от человека не только орудие (подобно Марксу), но и интеллект. Интеллект перестал быть человеческой характеристикой: отныне он – изолированная в машине и поэтому измеримая экономическая величина, такая же, как мощность и энергия. В пояснительной записке по случаю присуждения Бэббиджу премии Лондонского астрономического общества говорится:

В иных случаях механические устройства заменили более простые инструменты или физический труд машинами. […] Изобретение, которое я представляю, […] заменяет механическую силу интеллектуальным процессом. Изобретение мистера Бэббиджа заменяет компьютер машиной.

Под компьютером, конечно, подразумевался человек. Интеллектом теперь обладают и люди, и машины. Это позволяет точно рассчитать, кто более рентабелен – машины или люди:

Начальник фабрики (master manufacturer), разделив работу на несколько процессов, каждый из которых требует разной степени подготовки или физической силы, может получить ровно столько того и другого, сколько необходимо для каждого процесса; тогда как если вся работа выполняется одним ремесленником, то этот человек должен обладать достаточным мастерством и достаточной силой для выполнения наиболее тяжелых и трудоемких операций, на которые делится производство.

До этого момента интеллект был присущ человеку. Он был не случайным, а конститутивным признаком его как человека.

Как только машины наделяются интеллектом, исчезает принципиальная разница между человеком и машиной; оба предстают как равнозначные члены одной производственной цепи. Зачастую машины даже имеют преимущество, поскольку, как пишет Бэббидж, они не только быстрее и надежнее, но и внимательнее, трудолюбивее и честнее людей.

Маркс, усердно изучавший труды Бэббиджа, считал его мечту о совершенной экономике страшным сном капитализма. В дискуссии 1856 года о механизации труда он заявил: «Все наши открытия и весь наш прогресс как бы приводят к тому, что материальные силы наделяются интеллектуальной жизнью, а человеческая жизнь, лишенная своей интеллектуальной стороны, низводится до степени простой материальной силы». Год спустя Маркс заметил, что «машина, обладающая вместо рабочего умением и силой, сама является тем виртуозом, который имеет собственную душу в виде действующих в машине механических законов». Маркс предвидел ползучий переворот: человек превращается в машину, машина становится одушевленной.

Машинная экономика Бэббиджа вращается вокруг понятия интеллекта, или, лучше, разума, intelligence. В Оксфордском словаре зафиксированы два различных значения слова intelligence. Во-первых, оно относится к тому, чем занимается Центральное разведывательное управление США, а именно сбору (секретных) данных с целью наблюдения и контроля, а во-вторых, оно означает способность логически мыслить. Оба определения, взятые вместе, подразумевают, что интеллект – это способность принимать правильные решения на основе собранных данных.

Бэббидж определяет человеческий разум по аналогии с машиной: он обрабатывает информацию, принимает решения на основе этой информации и контролирует производственный процесс. Аналитическая машина, по его мнению, сможет делать прогнозы (forecast) на основе воспоминаний (memory) и действовать в соответствии с этими прогнозами. Мышь «Тесей» Клода Шеннона была первой машиной, которая действительно умела это делать.

Для программирования аналитической машины у Бэббиджа не хватало математических способностей. В этом ему помогла Ада Лавлейс. 42-летний Бэббидж познакомился с Августой Адой Байрон на светском мероприятии, когда ей было всего 17 лет. Бэббидж был глубоко впечатлен остротой ума и математическими знаниями дочери лорда Байрона и с тех пор поддерживал связь с семьей. Однажды он получил сделанный ею перевод статьи Менабреа об аналитическом двигателе на французском языке. В ответном письме Бэббидж спросил, не хочет ли она сама написать статью вместо того, чтобы переводить чужие. Ада не отважилась на это, ведь ей, как женщине, не разрешалось даже входить в библиотеку Королевского общества, где позже будет установлен ее бюст.

Она лишь добавила свои комментарии к переводу, и из этих комментариев, на которые, в свою очередь, ответил Бэббидж, складывается впечатление, что Ада – леди Лавлейс, как ее стали называть после замужества, лучше самого Бэббиджа понимала значение этой так и не созданной машины. Она писала:

Анализирующая машина включает два основных типа карт: во-первых, карты операций, с помощью которых части машины располагаются так, чтобы можно было выполнять любую конкретную серию операций – сложения, вычитания, умножения и деления; во-вторых, карты переменных, которые указывают машине столбцы, на которых должны быть представлены результаты. Когда карты начинают двигаться, они последовательно располагают различные части машины в соответствии с типом процессов, которые необходимо выполнить, и машина совершает эти процессы одновременно с помощью различных частей механизма, из которых она состоит.

Одни карты производят операции, другие принимают решения об операциях. Таким образом, леди Лавлейс изобрела компьютерную программу вместе с циклами и условными ветвями. Программируемость открывала бесконечное число возможностей для аналитической машины: она могла решить любую задачу, разложенную на отдельные шаги. Правда, Бэббидж не мог придумать ничего лучше и полезнее детской игры: «Я представляю себе машину, состоящую из фигурок двух детей, играющих друг против друга, и стоящих рядом с ними барашка и петуха. Ребенок, выигравший игру, хлопает в ладоши, и петух кричит, после этого побежденный ребенок плачет и разводит руками, а барашек блеет».

Примечательно, что Бэббидж фантазирует не о том, как его будущая машина играет против ребенка, а о том, что два ребенка-машины играют друг против друга. На первый взгляд это кажется гораздо менее зрелищным, чем игра машины против человека. Но он стремился представить себе мир, в котором человек и машина живут вместе. Поэтому для него не имеет значения, играют ли две машины друг против друга или человек играет против машины.

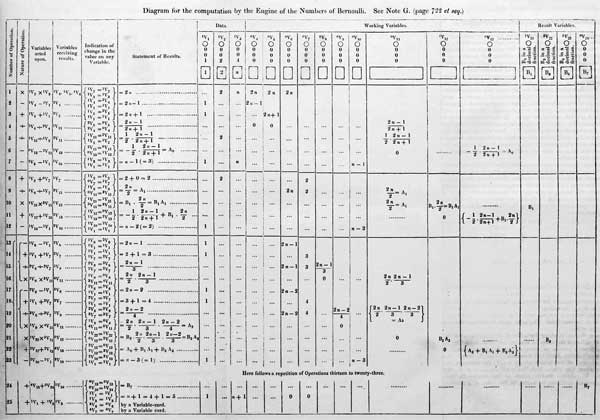
Таблица, разработанная Адой Лавлейс для вычисления чисел Бернулли

Впечатляет не машина как (искажающее) зеркало человека, а ансамбль человека и машины, созданный путем взаимной адаптации. Действительно, на многих выставках паровые двигатели и другие промышленные машины демонстрировались вместе с людьми за работой, воссоздавались даже целые заводские цеха.

За техническими и экономическими интересами Чарльза Бэббиджа стояли метафизические и религиозные наклонности. Бэббиджа никогда не интересовало только эффективное производство – его волновала тайна творения. Уже в Кембридже он основал Клуб привидений, который занимался научными исследованиями сверхъестественных явлений, в частности тех, о которых рассказывается в Священном Писании. Второй основанный им клуб, Клуб экстракторов, имел единственную цель – освобождать своих членов из сумасшедшего дома, если кто-то из них когда-нибудь окажется в нем, чего на самом деле нельзя было совершенно исключить, учитывая, чем они занимались: так, однажды Бэббиджу пришло на ум исследовать, каково это быть запеченным. К счастью, он отказался от этого эксперимента. Еще подростком Бэббидж придумал машину, с помощью которой можно ходить по воде, как когда-то Иисус Христос. Поэтому его сильно задели нападки со стороны отдельных религиозных деятелей.

В 1837 году в «Девятом Бриджуотерском трактате» Бэббиджу пришлось защищаться от обвинения священника Уильяма Уэвелла в том, что «механические философы» не могут ничего добавить к христианскому учению о Боге. Напротив, возражал Бэббидж, он выдвинул христианское представление о Боге, соответствующе его времени. Бог – это существо, которое принимает совершенные решения на основе всей доступной ему информации (memory) и таким образом определяет будущее (forecast). По сути, Бог почти не отличается от аналитической машины.

Этот довольно странный ответ раскрывает не только фантазии Бэббиджа о величии, но и его неявную метафизику: Бог – это экстраполяция человека, существо, которое мыслит как человек, но более совершенно. Соответственно, его машина могла не только имитировать человеческий разум, но и усовершенствовать его настолько, чтобы приблизиться к Богу.

Бэббидж не заметил, что он конструирует не только образ Бога, но и понимание человека как существа, которое прогнозирует будущее на основе имеющейся информации и исходя из этого принимает решения, – существа, похожего на его машину. Бэббидж создает не машину, имитирующую человека, как он думал, а человека, имитирующего машину.

С этого момента отношения между человеком и машиной сводятся не к тому, как человек отражается в машине, а к тому, как они взаимодействуют друг с другом. Чтобы взаимодействие было беспроблемным, человек, как в настольной игре, должен адаптироваться к машине, следуя набору правил, определяющих все возможные ходы. Тогда машина будет «понимать» человека и сможет отвечать ему соответствующим образом. Как в настольных играх или в карточной игре, успех участника зависит от того, способен ли он на основе информации о предыдущих ходах просчитывать следующие и принимать правильные решения. По мнению Бэббиджа, любой, кто может это сделать, разумен – человек или машина, не имеет значения. Поэтому неслучайно, что в фантазии Бэббиджа дети играют друг с другом. На смену зеркальному отражению как модели отношений между человеком и машиной пришла игра.

Поначалу мышление в парадигме игровых ходов было уделом лишь нескольких экспертов, которые работали на американских военных. Так было и с Норбертом Винером, который с помощью кибернетики смог заглянуть в мысли вражеского пилота, чтобы рассчитать его реакцию. Этот расчет производится с помощью рекурсивных рядов: результат одного расчета вместе с реакцией пилота переходит в следующий расчет в качестве начального значения – и так до тех пор, пока самолет не будет сбит.

Бэббидж был оправдан посмертно. Машина предвидит будущее намного лучше, чем человек. Она может рассчитывать будущее (forecast) на основе информации (memory).

Американские военные планировали использовать идею Винера в противовоздушной обороне и сделать ее основой новой комплексной стратегии. Исходя из нее предполагалось автоматизировать военную систему управления, опирающуюся на три C – связь (communication), командование (command), контроль (control). Впоследствии к этому настолько привыкли, что было решено использовать алгоритмический расчет при запуске атомной бомбы.

Свои наработки в области противовоздушной обороны Винер взял за отправную точку для интерпретации всей реальности как потока информации, который стремится к гомеостатическому состоянию, достигаемому и поддерживаемому с помощью механизмов обратной связи. Отсюда возникла новая отрасль науки – кибернетика – наука об управлении. Кибернетика рассматривает все с точки зрения контура управления. Система должна выполнять определенную задачу; когда возникает угроза отклонения от цели, она регулирует свое состояние на основе обратной связи, чтобы вернуться к прежнему курсу. Например, система отопления должна нагревать помещение до 18°C (так называемая управляемая переменная). Если модуль управления получает от датчика информацию о том, что температура в комнате составляет 21°C, то он уменьшает нагрев до тех пор, пока снова не будет достигнуто управляемое значение.

Тем самым Винер реализовал мечту Бэббиджа о понимании Вселенной как игры, где проигрывается один ход за другим и нет разницы, кто играет, машина или человек. В игре Бэббиджа актор делает ход, вынуждая противника сделать ответный ход; в игре Винера актор посылает информацию, которая побуждает ее получателя совершить некоторое действие, точнее говоря, заставляет его принять решение.

Интеллект для Бэббиджа – то же самое, что информация для Винера: понятие, которое делает человека и машину равноправными обитателями одного и того же мира. Информация может быть как материальной, так и нематериальной, аналогично и решения принимаются людьми или машинами. Паровому двигателю все равно, кто принимает решение об открытии клапана для снижения давления в котле, Гемфри Поттер или центробежный регулятор. В мире кибернетики Винера больше нет различий между телом и разумом, человеком и машиной.

Здесь не место для введения в кибернетику или теорию информации. Мы лишь хотим показать, как появление машины компьютера способствовало рождению нового образа мышления, полностью основанного на принятии решений. Мыслить – значит выбирать между возможностями на основе информации. Людям необходимо адаптироваться к этой форме мышления, если они хотят взаимодействовать с машинами.

Одним из первых, кто осознал это, был Ванневар Буш. Некоторое время Буш был одним из самых влиятельных людей в США: он руководил и координировал все военные исследования в области компьютеров.

После окончания Второй мировой войны, когда многие ученые, математики, физики и биологи, работавшие в армии США, остались без работы, в журнале The Atlantic Monthly вышла программная статья Буша под названием «Как мы можем мыслить». В ней речь идет о том, в каком направлении должны развиваться научные исследования в будущем.

Самой большой проблемой, стоящей перед наукой, Буш назвал управление накопленным объемом знаний, особенно возросшим за время войны. Ни один человек уже не в состоянии охватить эти знания, для этого нужны машины:

Речь идет о гораздо более серьезной проблеме, чем простой сбор данных для целей научного исследования, а именно о том, как люди используют наследие приобретенных знаний. Самый важный акт использования – отбор, и на этом мы, собственно, остановились.

Важнейшая задача науки – это отбор знаний, и эту задачу может взять на себя только компьютер: вместо перегруженного ученого он решает, что важно, а что нет.

Клод Шеннон, отец теории информации, придерживается аналогичной точки зрения:

Основной задачей связи является восстановление (точное или приближенное) в данной точке сигнала, отправленного в другой. Часто сигнал имеет некое значение, то есть соотносится или коррелирует с заданными состояниями некоторой системы. Однако эти семантические аспекты связи не имеют отношения к инженерной задаче, важно лишь то, что сообщение выбирается из некоторого набора возможных. Система связи должна одинаково хорошо работать со всеми возможными вариантами сообщения, а не только с тем, который будет выбран в действительности – на этапе разработки системы это еще не известно.

Коммуникация, совместимая с компьютером, не имеет ничего общего со смыслами, это игра между человеком и машиной, игра с ходами по установленным правилам.

До изобретения персонального компьютера компанией Apple в 1976 году понимание мышления как игры оставалось делом немногих ученых. В наши дни, похоже, это захватило всех. Компьютерная игра стала парадигмой нового образа мышления, потому что в ней особым образом переплетаются человек и машина.

Большинство компьютеров принимают решения самостоятельно исходя из условий, заданных в программе. При этом существуют программы, которые на некоторых ветвях оставляют решение о дальнейшем ходе за пользователем. Компьютерная игра – это алгоритм, который на некоторых ветках предоставляет пользователю несколько вариантов. Правда, не все варианты равноценны. Здесь, как и в садовом лабиринте эпохи барокко, (обычно) только один путь ведет к цели, остальные заканчиваются тупиками. Чтобы добиться успеха, игрок должен не только тренировать свою ловкость, но и распознавать лучшие пути, которые приведут его к цели.

Чтобы добиться успеха, игрок должен адаптировать свое мышление к программе. Только если он приспособится к логике программы, он сможет принять правильное решение за доли секунды. В идеале сторонний наблюдатель уже не сможет определить, кто играет в игру – человек или машина. Тогда тест Тьюринга будет пройден не потому, что компьютер может сопереживать человеку, а потому, что человек может сопереживать компьютеру.

Подобно тому, как велосипед и велосипедист сливаются в единое целое, игроки и компьютеры также сливаются в единую систему. Искусство игрока заключается в том, чтобы стать частью программы, то есть выполнять следующие ходы так, как их выполняла бы соответствующая программа. Поэтому требуется эмпатия к машине.

Успешный игрок мыслит алгоритмами: решение о следующем ходе зависит исключительно от текущей ситуации, он перебирает возможные решения по принципу «если – то».

Адаптация человека к машине началась не с компьютера. Уже Маркс заметил, что рабочий на фабрике полностью приспосабливает свое тело к машине, чтобы поддерживать работу фабрики. Он берет на себя те производственные операции, на которые машина (пока) не способна. В фильме Чарли Чаплина «Новые времена» (1936) показано, что происходит, когда адаптация не удается: рабочий буквально попадает под колеса.

По Марксу, рабочий распоряжается только своей физической силой и временем жизни, но не своим сознанием. Более того, противоречие, что он вынужден продавать свою жизнь, чтобы жить, обостряет в нем сознание необходимости революции. Чем больше ему приходится приспосабливать свое тело, тем более неприспособленным становится его сознание. Позднее Георг Лукач ввел возможность ложного сознания, то есть сознания, которое уже не сопротивляется, а приспосабливается, не осознавая этого.

Это приспособление иного рода, чем взаимодействие компьютера и человеческого разума или велосипеда и велосипедиста, которое мы обсуждали выше. На фабрике рабочий целиком ставит свои решения на службу машине: они навязываются функцией машины и потому служат выражением отчуждения рабочего, знаком его порабощения. Выбор игрока в отношении программы также не является следствием абсолютно свободной воли – он может выбрать только тот путь, который является частью программы, – однако связь между ними основана на логике взаимного обмена, а не подчинения. Игрок реагирует на программу, программа реагирует на действия игрока. Чем лучше они адаптируются друг к другу, тем успешнее игра. Адаптация не всегда означает подчинение и ложное сознание, ее можно понимать и как живой обмен с окружающей средой. Является ли что-то обменом со средой или подчинением иностранной власти, зависит от реального соотношения сил, а не от технологии, даже в современной, в значительной степени цифровизированной индустрии.

Отличительной чертой программируемого компьютера, по мнению Бэббиджа, является его способность предсказывать следующий ход. Действительно, сегодня главное занятие компьютеров и их алгоритмов – просчитывать желания людей.

Математическую основу для этого создал венгерско-американский ученый Джон фон Нейман. Кстати, он тоже служил в армии США.

Еще в юном возрасте, изучая квантовую физику, он познакомился с проблемой, которая затем сопровождала его на протяжении всей жизни: как заниматься математикой в условиях неопределенности? Это большая проблема не только квантовой механики, но и социальных наук. Конечно, для этого существуют статистические методы, но они пытаются минимизировать неопределенность с помощью закона больших чисел, тогда как Джон фон Нейман предлагает оперировать с неопределенностью. При этом он выдвигает простую и убедительную гипотезу: люди действуют на основе ожиданий относительно действий других. Зацепы, которые делает наш вражеский пилот, являются результатом его ожиданий в отношении поведения зенитчика, а тот, в свою очередь, целится туда, куда, как он ожидает, полетит пилот.

Впервые внутренний мир противника не просто постигается семантически, а становится математической задачей. Фон Нейману удается объединить дискурсивную рациональность социального с математической рациональностью машины. Он очень быстро понимает, какие возможности это открывает в области экономики: поведение индивида на рынке определяется не только его собственной предельной полезностью, как до этого утверждала Лозаннская экономическая школа Леона Вальраса, но в гораздо большей степени тем, какого поведения он ожидает от других, от своих конкурентов. Я покупаю акции Nestlé, потому что спекулирую на растущей цене. Но я делаю это не потому, что я убежден, что компания получает прибыль, а потому, что я предполагаю, что все остальные думают, как хорошо идут дела у компании, а значит, они будут покупать акции и цена акций продолжит расти. Но точно так же и все остальные спекулируют на желаниях друг друга.

Поэтому то, чего хочу я, не может быть независимым от того, чего хотят другие, а то, чего хотят они, в свою очередь, зависит от многих других игроков. Желание следует понимать не только как внутреннее событие, а скорее как цепочку желаний. Если желание представляет собой регулярный процесс, убежден фон Нейман, то для него должно существовать математическое решение. В результате они вместе с Оскаром Моргенштерном разработали теорию игр.

Суть этой теории заключается в том, что в первый раз из-за неопределенности игроки в системе принимают неоптимальное решение; к следующему разу они, подобно «Тесею» Шеннона, уже усвоили урок: каждый знает, чего хочет другой, поэтому теперь они в состоянии найти оптимальное решение. Здесь нет бессмысленного механического повторения, но результат первой ситуации в качестве обратной связи включается в расчеты второй: возникает алгоритм, способный вычислять ожидания от поведения других, сравнивая поведение одного с ожиданиями в отношении поведения других. Таким образом высчитывается социальное поведение, причем не просто как среднестатистическое, а как серийные констелляции ожиданий отдельного человека.

Успех теории игр был огромен, особенно в военной сфере, где создавались компьютеры, способные выполнять такие расчеты гораздо быстрее человеческого разума.

Благодаря теории игр корпорация RAND, аналитический центр армии США, получила возможность не только программировать зенитные ракеты, но и предсказывать поведение Советов в холодной войне. Теперь компьютер мог принимать решения не только о поведении торпед и зенитных ракет, но и о возможном сбросе атомной бомбы. По крайней мере теоретически.

Война окончательно превратилась в игру. Вскоре за ней последовала экономика.

В 1990-х годах закончилась холодная война. Многие физики и математики остались без работы. Им пришлось искать новые сферы деятельности. На конгрессе американских физиков в 1996 году его президент Георг Пимбли обратился с предложением поделиться своими знаниями с крупными финансовыми учреждениями на Уолл-стрит. В итоге, например, компания Lehman Brothers создала отдел для физиков и математиков, которые нашли применение для алгоритмов теории игр на финансовом рынке.

Это радикально изменило рынок. Решения о покупке и продаже акций теперь принимались не на основе объективных данных о компании, а на основе расчетов ожиданий, надежд и страхов участников рынка. В уравнении Блэка – Шоулза расчеты основываются на желаниях участников рынка. Уравнение Блэка – Шоулза – это математическая модель, с помощью которой можно рассчитать финансовые опционы, представленная в 1973 году Фишером Блэком, Майроном Шоулзом и Робертом Мертоном. В 1997 году за эту разработку они получили Нобелевскую премию по экономике.

Так машины научились за считаные секунды просчитывать желания людей. Поскольку в сфере финансов часто счет идет на секунды, машинам также предоставили возможность принимать решения о покупке. Разум окончательно превратился в машину. Более того, ни один крупный игрок на рынке больше не может позволить себе обходиться без компьютеров. Поэтому состав рынка изменился: теперь игроками являются в основном не люди, а машины. По сути, алгоритмы вычисляют не человеческие желания, а желания других машин, заложенные в алгоритмы. Машины управляют другими машинами, как в игре Бэббиджа.

То, что машины могут предсказывать человеческое мышление или человеческие решения – насколько хорошо, еще предстоит выяснить, – несомненно, связано также с тем, что наше мышление в последние десятилетия незаметно адаптировалось к алгоритмам.

Мы научились мыслить как машины. Это кажется мне не менее впечатляющим, чем ворота храма, которые открываются как по волшебству.