Расчет поворотной лестницы с забежными ступенями

Выбирая конфигурацию лестницы, условно предполагают, что самым простым и удобным вариантом является прямой марш, далее следует лестница с площадкой. Менее удобной будет лестница с забежными ступенями и лишь в некоторых случаях используют винтовую.

Расчет параметров поворотных лестниц с забежными ступенями выполняется несколько иначе. Здесь уже необходимо оперировать такими понятиями, как средняя линия марша, радиус закругления средней линии и угол поворота марша.

Средняя линия марша при определении размера лестницы – это воображаемая линия, которая на прямых участках марша проходит строго по его середине, а на криволинейных – по линии, параллельной внутреннему краю марша, на расстоянии, равном половине его ширины. В тех же случаях, когда на поворотах внутренний край марша представляет собой круговую кривую, средняя линия параллельна ей. Центры окружностей обеих кривых в таких случаях совпадают, и те, кто еще не забыл совсем школьный курс геометрии, знают, что эти дуги являются частями концентрических окружностей. В иных же случаях средняя линия на повороте является ломаной кривой.

Величина радиуса закругления средней линии зависит от радиуса вписанной между маршами воображаемой окружности и от полезной ширины марша. Величина радиуса воображаемой окружности, вписанной между внутренними краями поворотного марша, для поворотных лестниц принимается равной 3050 см, определяется расчетом по габаритам предполагаемых к переносу по лестнице предметов обстановки и оборудования.

❐ Ширина забежных ступеней (размер лестницы) определяется по средней линии и должна быть, как и ширина прямых ступеней, постоянной величиной на всем протяжении лестницы.

В тех случаях, когда средняя линия является воображаемой круговой кривой, ширина ступеней определяется по хордам, соединяющим точки пересечения средней линии с горизонтальными проекциями граней ступеней.

❐ Ширина марша в пределах криволинейного участка лестницы принимается по направлению радиуса средней линии.

❐ Длина горизонтального заложения поворотного или кругового марша при определении размера лестницы определяется также по средней линии.

Угол поворота марша – это угол, образованный на горизонтальной проекции лестницы между створами внешних граней первой и последней ступеней марша.

Особенности расчета маршей с забежными ступенями (размер лестницы) заключаются, во-первых, в несколько иных методиках расчета габаритов горизонтальной проекции, зависящих от типа лестницы, и, во-вторых – в раскладке и определении размеров ступеней на его криволинейных участках.

Наиболее характерными для иллюстрации особенностей расчета маршей с забежными ступенями являются четвертьоборотные, полуоборотные и винтовые одномаршевые лестницы.

Общий вид лестницы, взятой при расчетах за основу.

В приведенном примере единственно возможным вариантом является расположение лестницы вдоль наружной стены дома с пересечением окон, хотя в этом случае конструкция ограничивается радиатором отопления и габаритами проема. Это яркий случай неверного подхода к проектированию лестницы, когда она встраивается в уже существующие строительные конструкции, а не проектируется совместно со зданием.

На стр. 84 изображена лестница, на примере которой в дальнейшем будет проиллюстрирован порядок расчета поворотной Г-образной лестницы с забежными ступенями. Эта лестница наряду со своей простотой может продемонстрировать последовательность расчетов по размещению лестницы, определению ее параметров и конструктивных особенностей. Особенностью этого расчета является то, что лестница встраивается в уже готовые строительные конструкции с имеющимся проемом и планировкой сообщающихся этажей. При этом чаще всего бывает единственно возможный вариант, хотя на этапе эскизной проработки можно попытаться вписать различные лестницы.

Встраивать лестницу в здание на стадии проектирования проще, но общий ход рассуждений очень похож. Приведенные ниже расчеты можно производить при замерах.

На начальном этапе расчетов прежде всего определяется линия хода для данной лестницы, поскольку не всякий вариант ее расположения может быть применим на практике. Линией хода будем называть горизонтальную проекцию условной линии, проходящей по рабочим ребрам ступеней на расстоянии 300–500 мм от внутреннего края лестницы. Такой размер берут из соображений удобства пользования поручнем. Величина эта средняя, поскольку люди невысокого роста и дети ходят ближе к поручню, высокие взрослые – дальше. Для прямых маршей размер этот не играет большой роли, поскольку плоскости ступеней параллельны. Не старайтесь расположить эту линию, как иногда рекомендуют, посередине забежных ступеней. На широкой лестнице (хотя бы 1200 мм) вы просто не дотянетесь до поручня.

Определяя размеры ступени, можно воспользоваться рекомендованными размерами подъема и проступи h × а = 150 × 300, 160 × 300 и 170 × 290 мм, которые действительно удобны, хороши для проектирования, но не применимы, если дом уже простроен и высота лестницы (Н) не кратна (h). Также существуют формулы «удобства» (а – h = 120 мм) и «безопасности» (а + h = 450 мм). К сожалению, они действуют только в очень узком диапазоне размеров.

Более универсальный способ был предложен французским архитектором Франсуа Блонделем в 1672 году. Он использовал формулу а = 5 – 2/7, где 5 – параметр, называемый «средний шаг человека», обычно принимаемый 600–640 мм. Эта формула повсеместно используется и по сей день. Выражение а = S – 2h легко преобразуется в более удобное для использования неравенство 600 < а + 2h < 640 мм. Нижним пределом применения этой формулы обычно считают минимальный подъем ступени h = 120 мм, а = 400 мм, уклон 17°.

Из всего вышеизложенного следуют выводы. Для проектирования лестниц на стадии разработки чертежей дома следует принимать 600 < а + Zh < 640 мм. Для проектирования лестниц, встраиваемых в уже существующие здания, можно воспользоваться более широким интервалом значений, например, использовать стандарт, применяемый в Англии и Уэльсе: 550 < а + Zh < 700. Высота подъема ступени от 150 до 190 мм удобна, предельная высота по СНиП 21-01-97 – 220 мм. Спускаться по лестнице опаснее, чем подниматься, поэтому удобство хода надо оценивать именно «на спуск».

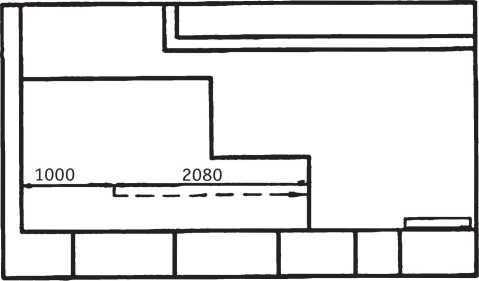
Вариант с прямым маршем (негодный).

Вариант с прямым маршем (стрелкой указано место выхода на второй этаж) не годится из-за слишком большой крутизны. В принципе, такие крутые лестницы делают из экономических соображений, поскольку они действительно намного дешевле; но в данном случае комфортом и эстетикой пренебрегать нельзя.

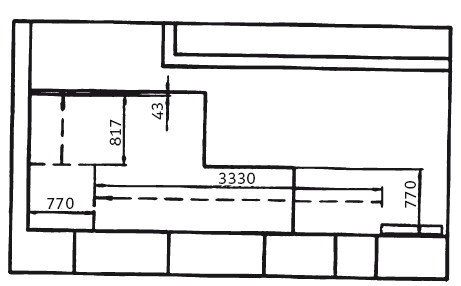
Вариант с прямым маршем с выходом у угла (негодный).

В этом варианте у лестницы, как говорят, теряется «критическая высота», т. е. человек будет наклонять голову при проходе около грани перекрытия. Кроме того, требуется устройство дополнительной площадки на втором этаже; поэтому вариант такой лестницы на практике также непригоден.

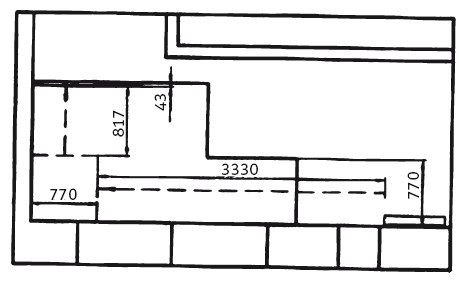
Вариант угловой лестницы с прямолинейными маршами и угловой площадкой.

Этот вариант лестницы вполне жизнеспособен, поскольку длина хода А = 3330 + 817 = 4147 мм достаточна даже без учета проступи площадки. При n = 18 проступь равна а = 4147: (18-1) = 244 мм и параметр шага 169 x 2 + 244 = 582 мм.

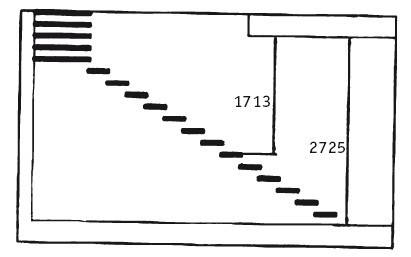
Определение критической высоты.

При построении ступеней на разрезе видно, что расстояние между лестницей и перекрытием слишком мало: 1712 < 2000 мм и увеличить это расстояние можно, лишь изменив проступь и увеличив крутизну лестницы, что в дальнейшем и будет сделано. Весьма полезно для каждого варианта линии хода рассматривать по три варианта количества ступеней.

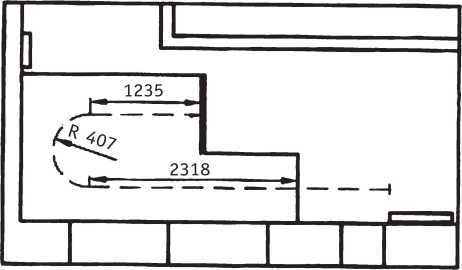
Вариант П-образной лестницы с забежными ступенями.

В этом варианте линию хода можно начинать даже не от батареи, а от проекции начала проема. При этом А = 4831 мм. При n = 18, h = 169 получается проступь, равная а = 284 мм, что вполне соответствует нормативным требованиям. Проверка по формуле 2h + a = 169 x 2 + 284 = = 622 мм также дает положительный результат.

Критическая высота в этом случае очевидно более 2000 мм.

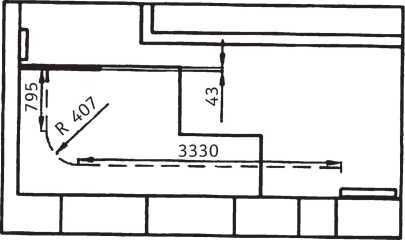
Вариант Г-образной лестницы с забежными ступенями.

В этом случае длина хода составляет А = 4773 мм. Рассчитываем проступь при n = 18, h = 169, получаем а = 280 мм. Проверка по формуле 2h + а = 169 × 2 + 28 = 618 мм указывает на приемлемость варианта. Критической высотой у этого варианта будет расстояние от нижнего ребра перекрытия до ступени, которую легко определить при расчете. 3330–2318 = 1012 мм – расстояние от начала лестницы до проекции ребра. В этот промежуток уложатся 1012:280 = 3,6 ступени, т. е. под проемом будет находиться четвертая ступень. Ее высота от пола составляет 169 x 4 = 676 мм. Над головой в самом низком месте остается 2727 – 676 = 2051 мм, что вполне достаточно.

Из-за разницы шага правой и левой ног предпочтительны лестницы с левым заходом – спускаться по ним удобнее.

В данном конкретном случае высоту ступени h очень легко определить делением высоты лестницы Н (расстояние от пола до пола) на предполагаемое число (п) подъемов. Во всяком случае число ступеней должно быть целым. В нашем примере можно задаться такими значениями: если Н = 3050 мм, то при 17 подъемах h = 3050: 17 = 179,4 мм, при 18 подъемах h = 3050: 18 = 169,4 мм и при 19 подъемах h = 3050: 19 = 160,5 мм.

Следовательно, последние три варианта теоретически удовлетворяют основным требованиям и могут использоваться для детальной проработки. Последний вариант является самым дорогим и трудоемким.

Таким образом, у варианта с угловой площадкой уклон марша 35°, h/a = 179/259 мм. У варианта с забежными ступенями уклон марша 32° и h/a = 169/275 мм. Показатели второго варианта лучше, но у него вместо площадки будут забежные ступени, что несколько усложняет конструкцию. Принимая во внимание эстетический аспект, можно остановиться на варианте с забежными ступенями и приступить к его детальной проработке.

Чтобы ходьба по криволинейному маршу была максимально приближена к ходьбе по прямому, а на переходе с прямолинейного участка на криволинейный у человека не возникало ощущения резкого изменения темпа и направления шага, угол поворота марша (угол наклона лестниц) должен быть распределен между как можно большим количеством забежных ступеней, а углы поворота ступеней плавно нарастать от входа на криволинейный участок до его середины и уменьшаться от нее до выхода из криволинейного участка. Разумеется, при таких условиях размеры забежных ступеней будут отличаться друг от друга. Этот принцип устройств забежных ступеней не распространяется, однако, на винтовые лестницы, все ступени в которых должны быть абсолютно одинаковыми по размерам и форме. Но винтовые лестницы и не считаются удобными и сооружаются обычно только в стесненных планировочных условиях.

Точный математический расчет размеров и положения забежных ступеней четвертьоборотных и оборотных лестниц относительно средней линии марша довольно утомителен и сложен. Поэтому на практике прибегают к раскладке забежных ступеней при помощи разных графических способов.

Наиболее употребительными являются метод пропорциональной разбивки, метод вспомогательных линий и метод полуокружности. Они применимы практически для всех типов поворотных лестниц, но предполагают разный принцип раскладки ступеней относительно линии, делящей угол поворота марша пополам (биссектрисы).

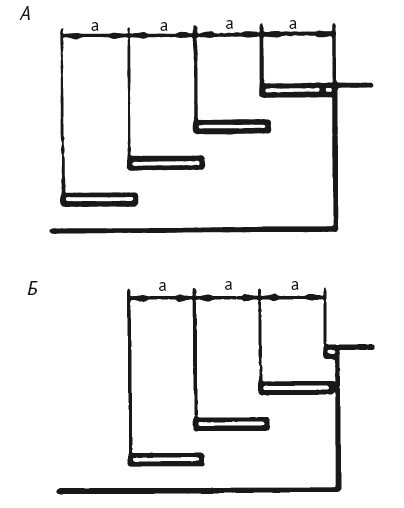
Деление линии хода на количество ступеней (А – деление на n, Б – деление на n – 1).

В вопросе, на сколько частей делить линию хода – n или n – 1, существует некоторая путаница. Разница в том, как приходит к верхнему перекрытию ступень. Обычной задачей (ив нашем варианте 5 тоже) является максимальная компактность лестницы. Тогда мы в качестве последнего подъема используем часть строительной конструкции перекрытия или стены, прикрепляя к ней «нос», чтобы выгадать один подъем ступени; линию хода делим на n -1. Но иногда бывают настолько просторные помещения, что этот способ применять нет нужды и последнюю ступень можно ставить вровень с полом; линию хода делим на n. Следует заметить, что линия хода заканчивается не на грани строительной конструкции, а на ребре последней ступени. Поэтому необходимо отступать от перекрытия на размер носа + толщина облицовочной доски, обычно это 25 + 18 = 43 мм.

Чаще всего вариантов расположения лестницы бывает немного – один-два, но бывает и столько (причем равноценных!), что выбор оптимального решения превращается в непростую задачу с привлечением экономических расчетов.

Итак, последовательность расчетов будет следующей:

❐ Измерив высоту лестницы, определяют несколько вариантов подъема ступени h и количества ступеней (n), сначала исходя из интервала 160–200 мм.

❐ Далее выбирают начало и конец лестницы из соображений удобства планировки дома и движения людей по нему.

❐ Определяют зоны, которые ни в коем случае не должны перекрываться конструкцией лестницы.

❐ При помощи мела и отвеса на полу намечается примерная линия (или линии) хода.

❐ Рулеткой измеряется ее общая длина, которая сравнивается с высотой лестницы. Если длина линии хода в 1,7 раза больше высоты, это соответствует уклону 300.

❐ Линия хода делится на количество ступеней n или n – 1, по имеющимся вариантам подъема ступени. Получатся несколько вариантов размера проступи.

❐ Следует подставить попарно каждый результат в формулу Блонделя и выбрать наилучший.

❐ Тщательно проверить критическую высоту. При этом можно применить один практический способ с нанесением расположения ступеней на стене или (если лестница не примыкает ни к одной стене) на достаточно крупном куске листового материала. Если отложить от критической точки (за которую можно задеть головой при движении по лестнице) 2000 мм по вертикали, то сразу станет видно, проходит ли по высоте такое расположение ступеней.

❐ Забежные ступени можно располагать и вне криволинейного участка средней линии, что делает поворот более плавным. Чем больше забежных ступеней находится на прямых участках средней линии, тем удобнее передвижение по лестнице.

❐ Ширину забежных ступеней определяют по средней линии. Она должна быть равна ширине прямых ступеней.

Раскладка ступеней производится на плане горизонтальной проекции лестницы, вычерченном строго по расчетным габаритам марша в соответствии с приведенными выше методиками. План составляется на специальной бумаге с нанесенной типографским способом координатной сеткой (миллиметровке) в произвольном масштабе, позволяющем достаточно точно отложить, например, ширину ступени. Подходящим для этого является масштаб 1: 10, при котором 1 – единица длины отрезка на плане соответствует 10 единицам этого же отрезка в натуре.

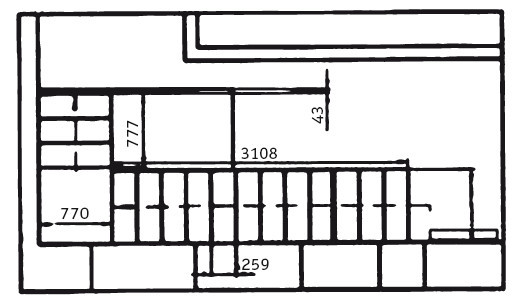
Измененный вариант угловой лестницы с прямолинейными маршами.

В варианте с поворотной площадкой (с. 87) можно поделить высоту не на 18, а на 17 подъемов (h = 3050:17 = 179 мм). Соответственно увеличится и проступь (а = 4147:16 = 259 мм). В этом случае параметр шага 2h + а = 179 × 2 + 259 = 618 мм стал гораздо лучше. Поскольку в размер проекции линии хода второго марша 817 мм нацело не укладываются ни а = 244 мм, ни а = 259 мм, придется несколько изменить размер площадки и после этого пересчитывать количество подъемов в первом и втором маршах. Из рисунка видно, что несмотря на увеличение подъема ступени на 10 мм, параметры лестницы заметно улучшились. Длина линии хода сократилась из-за уменьшения количества проступей. Критическая высота находится на четвертой ступени и расстояние до перекрытия стало 2725 – (179 × 4) = 2009 мм.

Перед тем как начать раскладку забежных ступеней, на план марша наносят среднюю линию и ось симметрии, которая для четвертьоборотной лестницы проводится из вершины угла поворота марша через центр круговой средней линии, а для полуоборотной – через центр кривой и точку, разделяющую торцевой наружный край марша на два равных отрезка. После этого можно приступать к раскладке забежных ступеней.

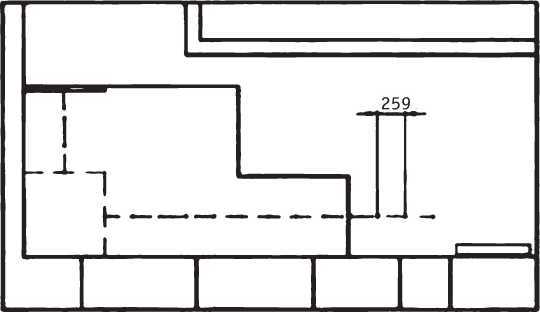
Разметка ступеней с прямой линией хода.

Разметка ступеней с прямой линией хода не представляет каких-либо затруднений. Главное – считать не ступени, а подъемы, и не забывать про носу выхода с лестницы.

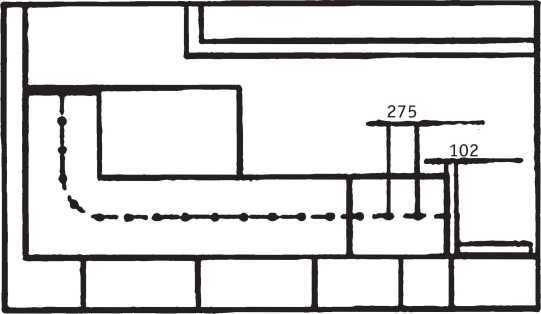
Измененный вариант лестницы с забежными ступенями.

В варианте с забежными ступенями (см. с. 89) изменений не так много. Прежде чем начинать его вычерчивать, полезно обратиться к таблицам стандартных деталей. В принятом варианте h = 169 мм и а = 280 мм. Ширина стандартной ступени 300 мм, на носу нас остается всего 20 мм, что для открытой лестницы без подступенков маловато, да и начинать лестницу прямо от радиатора отопления нехорошо. Примем окончательно: h = 169,4 мм и а = 275 мм. Параметр шага 169,4 × 2 + 275 = 614 мм. Линия хода уменьшается и составляет 275 × (18-1) = 4675 мм. В результате мы отступили от радиатора отопления на 102 мм. Такую операцию по переносу начала линии хода приходится делать достаточно часто для удобства монтажа ступеней относительно строительных конструкций и коммуникаций.

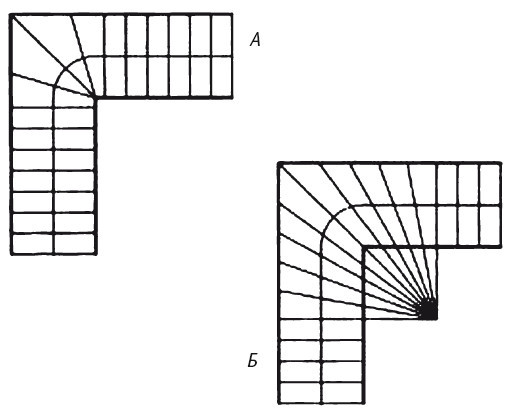
Угловая и отдаленная лучевая разметка лестницы с криволинейной линией хода.

Если линия хода криволинейная, то разметку ступеней можно выполнить разными способами.

При использовании простой лучевой разметки марши остаются прямыми, что упрощает технологию изготовления. Еще более упрощает разметку примитивное деление площадки на две, три или четыре части (А), но при этом, как правило, нарушается размер проступи, и получается «извилистая линия хода». Простота в данном случае не всегда уместна. При спуске с такой лестницы надо быть крайне осторожным при повороте. Естественно, хочется каким-либо образом раздвинуть ступени в том месте, где они образуют вертикаль на повороте. Эта задача называется децентрализацией ступеней, и решается она изменением способа разметки. Например, можно отодвинуть точку, из которой мы проводим разметочные лучи, на некоторое расстояние от угла (Б). На первый взгляд кажется, что цель достигнута и ступени встали ровно и удобно. В дальнейшем будет показано, что это совсем не так. Впрочем, лучевой способ разметки незаменим для лестниц с круговой линией хода и близкими к ней криволинейными и, прежде всего, для винтовых лестниц.

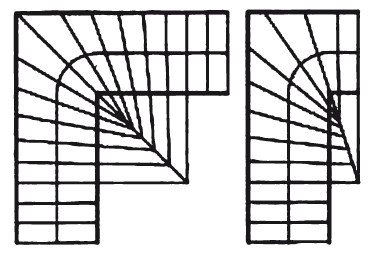
Метод пропорций для лестниц с криволинейной линией хода.

Неплохие результаты можно получить, используя метод пропорций. Суть метода заключается в том, что сначала размечают одну из ступеней, примыкающих к повороту, из расчета 120 мм в самой узкой части. Далее находят пересечения диагональной вспомогательной линии с проекцией грани размеченной ступени и границей прямых ступеней. Получившийся на диагонали отрезок делят в соотношении 1:2:3:4:5: 6… по числу забежных ступеней с каждой стороны от диагонали. Полученные точки соединяют с точками деления линии хода и получают разметку ступеней. К недостаткам способа следует отнести некоторую сложность точного геометрического построения, которое надо выполнять либо в крупном масштабе, либо на полу в натуральную величину. Этот метод можно применять и для неполных забегов.

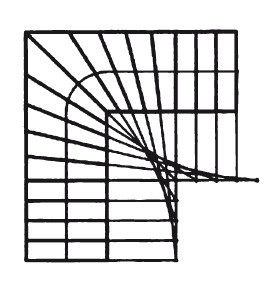
Разметка забежных ступеней при помощи вспомогательных линий.

Этот верный, удобный и наиболее распространенный способ разметки ступеней пришел из курса начертательной геометрии. Его суть понятна из рисунка. Все дальнейшие нужные построения будут основаны на нем.

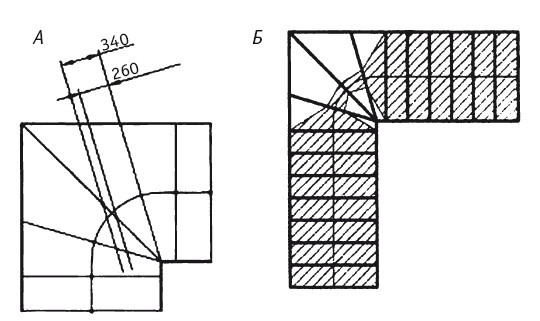
Разметка полосы хода.

Чтобы сравнить приведенные выше способы разметки, надо подобрать некий критерий, отражающий качество разметки ступеней и самой лестницы. Из иллюстраций видно, что забежные ступени на повороте к внутреннему краю уже, к наружному – шире. По самой линии хода мы отложили промежутки, равные проступи. Но человек не может идти точно по этой линии, а всегда будет отклоняться вправо или влево. Чем больше возможность такого отклонения, тем удобнее лестница. На повороте по внешней части ступеней шаг будет шире, по внутренней – уже. Зададимся достаточно широким, но обоснованным диапазоном параметра шага, например 570 < S < 650. Предположим, что в рассматриваемых примерах по линии хода а = 300 мм, h = 155 мм. По формуле Блонделя рассчитаем условную проступь справа: 570 – 2 × 155 = 260 мм и слева 650 – 2 × 155 = 340 мм. Теперь, исходя из предположения, что человек шагает перпендикулярно рабочему ребру ступени, на вычисленных расстояниях проведем линии параллельно такому ребру и отметим точки пересечения со следующей ступенью (А). Повторим эту операцию для всех забежных ступеней. Соединим отмеченные точки ломаной линией и заштрихуем многоугольник.

Получившуюся фигуру будем называть впредь «полосой хода». Чем шире эта полоса и чем удобнее она расположена по отношению к перилам, тем легче идти по лестнице. В случае простой лучевой разметки (Б) полоса хода на повороте настолько узка, что не только два человека в этой зоне не разойдутся, но и одному надо быть предельно внимательным. Кстати, по этим причинам пожарные запрещают использовать лестницы с забежными ступенями в общественных зданиях.

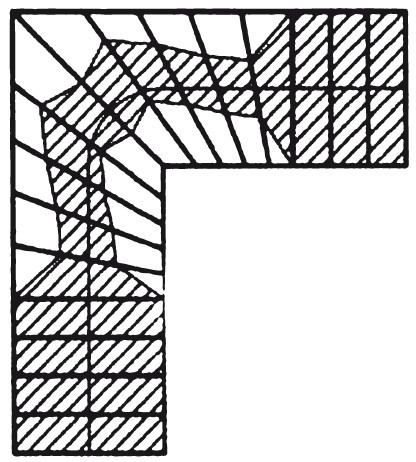
Ломаная линия хода при лучевой разметке ступеней с отдаленной точкой деления.

Еще интереснее получается картинка лучевых ступеней с отдаленной точкой деления. Внешне ровные ступени имеют извилистую полосу хода – тут недолго и споткнуться. Причины этих недостатков просты – лучевая разметка пригодна только для линий хода, состоящих из дуг окружностей или близких к ним. Такие линии хода встречаются нечасто, поскольку в наших домах преобладает прямоугольная планировка. Тем не менее такие лестницы строят и они будут рассмотрены.

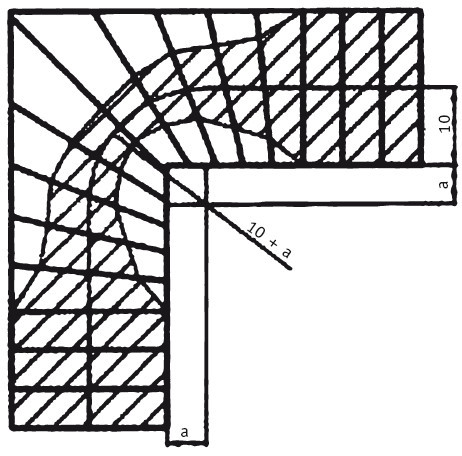
Расширенная полоса хода при расчете лестницы методом пропорций.

В рассмотренном выше примере радиус закругления линии хода на повороте был взят как расстояние линии хода от внутреннего края лестницы (lo). Радиус можно увеличить, но при этом обязательно пересчитать всю линию хода и точки деления. Как видно из рисунка, при изменении радиуса линии хода на ширину проступи полоса хода приблизилась к перилам и выровнялась относительно линии хода, линия хода на забежных ступенях становится слишком неперпендикулярной к рабочим ребрам. Отметим, что в качестве примера рассматривается крайний случай, когда децентрализация захватила десять из шестнадцати ступеней лестницы, чтобы максимально расширить полосу хода. На практике этого обычно не требуется, и в качестве некоторой «золотой середины» границами прямых ступеней выбирают третью или четвертую ступени, считая от поворота в каждую сторону.

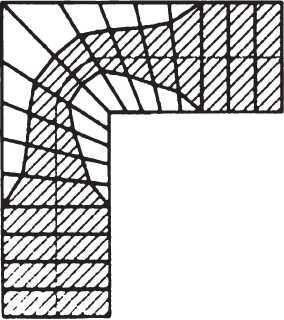
Зауженная полоса хода при расчете лестницы методом пропорций.

Пропорциональные системы разметки примерно равноценны, но способ пропорций требует виртуозной техники черчения или компьютерной графики. Как видно из рисунков пропорциональных способов разметки, полоса хода на повороте отклоняется недопустимо далеко от перил.

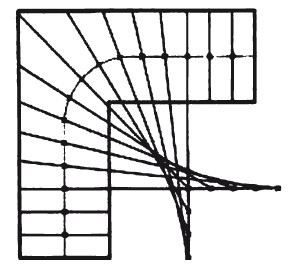
Полоса хода при разметке ступеней методом вспомогательных линий.

Этот способ позволяет по-разному расположить ступени, и полоса хода при этом меняется мало. Очень большим удобством способа разметки ступеней при помощи вспомогательных линий является его независимость от положения угловой ступени. Более того, сами вспомогательные линии могут и не совпадать с границами прямых ступеней.

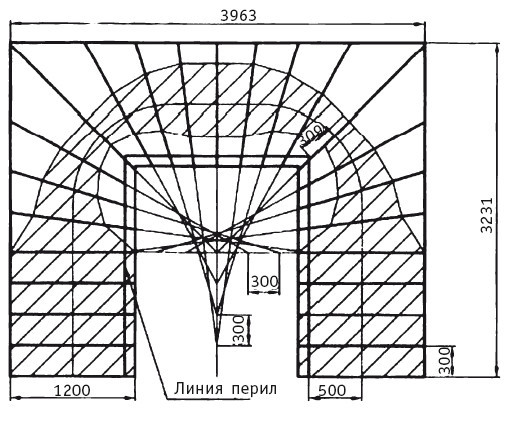
Разметка П-образной лестницы с двумя вспомогательными линиями.

При расчете лестниц сложной криволинейной конфигурации их, как правило, разбивают на более простые участки, комбинируя их между собой. Для П-образной лестницы с шириной проема между маршами больше, чем две проступи, применяют способ с двумя вспомогательными линиями. Надо сказать, что разметка с забежными ступенями позволяет построить вполне удобную лестницу, у которой размеры лестничной клетки меньше высоты лестницы. Из рисунка видно, что при габаритах лестницы в плане 3250 × 4000 мм она может подниматься на 170 × 25 = 4250 мм, при этом угол подъема составляет лишь 30°.

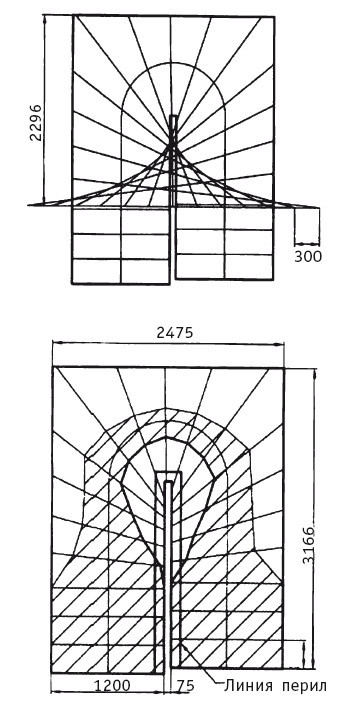
Разметка с одной вспомогательной линией.

При минимальном расстоянии между маршами в свету, равном по противопожарным требованиям 75 мм (чтобы проходил рукав пожарного ствола), применяют разметку с одной вспомогательной линией.

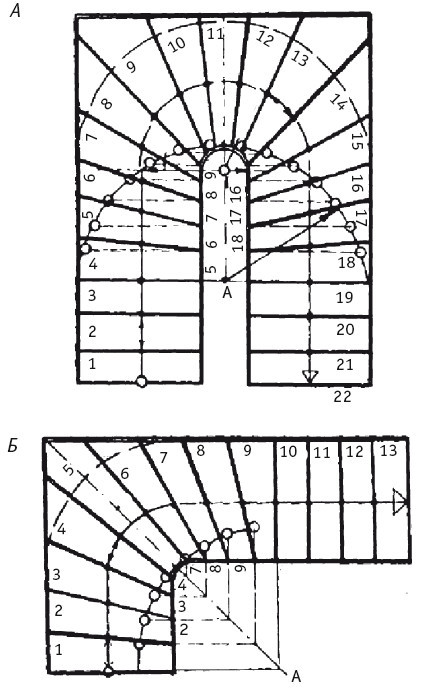
Примеры построения забежных ступеней методом полуокружности:

А – полуоборотного марша; Б – четвертьоборотного марша. Используя для построения забежных ступеней метод полуокружности, среднюю линию разбивают на отрезки, равные ширине ступени, таким образом, чтобы на ось симметрии попала продольная ось одной из ступеней. Ширина этой ступени в зоне примыкания к внутреннему краю марша выбирается произвольно, но должна быть не менее 10 см и не более, разумеется, диаметра воображаемой окружности, вписанной между внутренними краями марша.

Определяется положение последних прямых ступеней, которые будут находиться перед забежным участком марша. Створы граней этих ступеней соединяются прямой (при повороте марша на 180°) или ломаной (при повороте марша на 90°) линией.

Из точки пересечения этой линии с осью симметрии марша (точка А) описывают полуокружность радиусом АВ, равным, как видно из рисунка, расстоянию между этой точкой и точкой пересечения оси симметрии с внутренним краем марша (точка В). Эту полуокружность разбивают на равное количество отрезков, соответствующее количеству предусматриваемых забежных ступеней. Разбивка полуокружности ведется от точки В. О правильности и точности разбивки будет свидетельствовать симметричное положение отрезков относительно друг друга по обе от оси симметрии марша. Далее, из концов отмеченных на полуокружности отрезков параллельно линии, соединяющей грани прямых ступеней, проводят линии до пересечения с ближайшим внутренним краем марша. Из точек пересечения этих линий с внутренним краем марша (некоторые из них помечены на рисунке цифрами со штриховой пометкой) проводят линии через точки разметки ступеней на средней линии. Положение этих прямых в пределах марша и определит положение наружных граней раскладываемых забежных ступеней.

После того как забежные ступени разложены на плане марша одним из предложенных здесь способов, остается как можно точнее снять с чертежа размеры каждой и проверить, соответствует ли суммарная ширина их широких и узких торцов расчетным размерам соответственно наружного и внутреннего краев участка марша, на котором предусматриваются забежные ступени. Для этого необходимо рассчитать длины наружного и внутреннего краев горизонтальной проекции участка марша с забежным и ступенями (из общей длины каждого края горизонтальной проекции марша вычесть суммарную ширину прямых ступеней) и сравнить их с суммарной шириной соответственно широких и узких торцов забежных ступеней. Полученные погрешности распределить в равных долях между всеми забежными ступенями.

В заключение довольно кропотливой, но интересной процедуры раскладки забежных ступеней графическим способом необходимо вычертить каждую из них с указанием полученных размеров лестницы (ступеней) по всем ее сторонам.

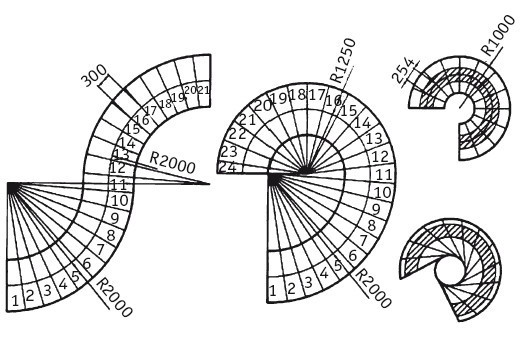
Построение ступеней криволинейных лестниц методом лучевой разметки.

В левой части рисунка изображены сложные по конфигурации лестницы с линией хода, размеченной дугами двух окружностей. Таких окружностей бывает несколько, и лестница напоминает в плане улитку или змею. Для винтовой лестницы (справа) приведены две разметки – прямая и касательная. Видно, что касательная разметка уводит полосу хода к перилам, не требуя сужения ступени по линии хода.

Из рисунков видно, что такое построение не должно вызывать каких-либо сложностей. Эти лестницы весьма красивы, хотя и менее удобны, чем прямолинейные. Для большинства из них требуются либо подготовленные заранее радиусные стены, либо опорные конструкции с трехмерной кривизной. Относительно легче сделать такую лестницу с несущим ограждением.

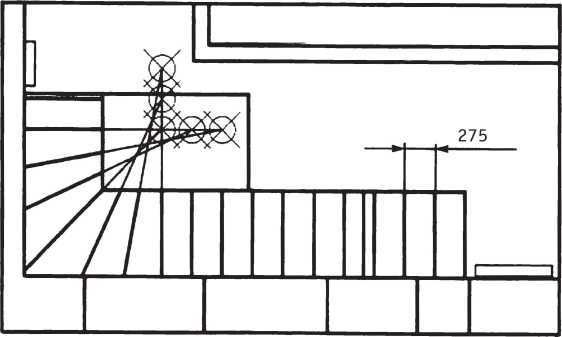
Разметка ступеней лестницы, рассмотренной ранее в качестве типового примера.

В качестве окончательного варианта в этой лестнице принимается наиболее прогрессивная разметка при помощи вспомогательных линий. Отступив от угла по три ступени, получим искомую разметку.