Когда Джон и Мэри Белл приехали в Соединенные Штаты, страна была погружена в глубокую скорбь. За день до того, как их самолет приземлился в Калифорнии, в Далласе был застрелен президент Кеннеди. «Из всех возможных дней приезда этот был худшим», – говорил потом Джон. Джон и Мэри, физики из Швейцарии, специализировавшиеся в области ускорителей частиц, получили приглашение поработать в течение года в противоположной точке земного шара, в Стэнфордском центре линейных ускорителей (SLAC). В этой атмосфере трагедии они и приступили к работе. «Мэри быстро втянулась в работу отдела, непосредственно экспериментировавшего с ускорителем, – вспоминал Джон, – а я оказался в группе, занимавшейся теорией [элементарных частиц]».

Джон воспользовался сменой обстановки как возможностью поработать над научными идеями, которые занимали его уже более десятилетия. С 1952 года, когда он прочел статьи Дэвида Бома, Белл знал: со знаменитым доказательством фон Неймана, которое, как считалось, показывает ошибочность бомовской теории волны-пилота и других подобных интерпретаций квантовой механики, что-то не так. Но другие физики все равно регулярно ссылались на фон Неймана, когда хотели объяснить, почему они игнорируют работы Бома. Незадолго до отъезда из Швейцарии Белл говорил с Йозефом Яухом, физиком из Женевского университета, который перед тем опубликовал свою «усиленную» версию доказательства фон Неймана. Развивая перед Беллом свои идеи, Яух, между прочим, рассказал ему еще об одном доказательстве, также подтверждавшем ошибочность версии Бома. «Это подействовало на меня как красная тряпка на быка, – рассказывал Белл. – Мне захотелось доказать, что Яух неправ. Последовало несколько довольно бурных споров». Теперь, окруженный непривычно безжизненным калифорнийским пейзажем, Белл приступил к выполнению своего плана. В ходе этой работы он открыл некую удивительную истину квантового мира – и в конечном счете ему удалось ослабить мертвую хватку копенгагенской интерпретации, сомкнувшуюся на горле квантовой физики.

Джон Стюарт Белл родился 28 июня 1928 года в Белфасте, в Северной Ирландии. Он был вторым из четверых детей в рабочей протестантской семье. По его собственному признанию, в его длинной родословной встречались «плотники, кузнецы, чернорабочие, сельскохозяйственные рабочие и торговцы лошадьми». Белл первым в своей семье окончил среднюю школу: отец его бросил учебу в восемь лет, все остальные дети к четырнадцати годам уже работали. Джон окончил самую дешевую школу в округе в шестнадцать, но в местный университет Куинс принимали только с семнадцати. Ему пришлось искать работу. «Я пробовал устроиться служащим в контору на маленькой фабрике, потом на Би-би-си, потом еще куда-то. Но меня никуда не брали», – вспоминал Белл много лет спустя. Наконец работа все же нашлась – ассистентом в физической лаборатории при университете. «Это было для меня огромной удачей – там я познакомился с моими будущими профессорами. Все были ко мне очень добры. Давали мне читать полезные книги. По сути, я прошел свой первый курс физики, убирая лабораторные помещения и готовя оборудование для студенческих лабораторных работ».

Ближе к окончанию своего университетского курса в Куинс Белл впервые познакомился с математическим аппаратом квантовой физики и с неизменно сопутствовавшей ему копенгагенской интерпретацией. То, что он узнал, ему не понравилось. «Сначала вы узнаете все о периодической системе элементов и обо всех остальных практических аспектах этой теории, – вспоминал Белл. – А потом начинаются загадки». И преподаватели Белла, и учебники рассказывали о природе волновой функции туманно. Они никогда не могли точно сказать, «была ли она [то есть волновая функция] чем-то реальным или просто некоторой разновидностью бухгалтерской операции». Но если волновая функция всего лишь инструмент бухгалтерского учета, устройство переработки информации, то кому эта информация принадлежит? И если никакого квантового мира, как настаивал Бор, не существует, о чем тогда рассказывает эта информация? Белл даже как-то поспорил об этом с одним из своих преподавателей. «Я очень разгорячился и в конце концов, по сути, обвинил его в нечестности. Он тоже разозлился и сказал: “Ты слишком далеко заходишь”. Но меня эта проблема очень уж глубоко задела – я был разъярен тем, что мы не в силах найти всему этому разумного объяснения».

Раздосадованный Белл, надеясь найти разъяснения, начал читать книги, написанные основателями квантовой физики. Но то, что он там нашел, не особенно ему помогло. Бор неясно очертил границу, по которой проходит раздел между квантовым и классическим миром. «Бора, по-видимому, оставляет совершенно равнодушным тот факт, что, обладая таким прекрасным математическим аппаратом, мы не знаем, к какой части нашего мира его следует применять, – говорил Белл. – Бор, по всей видимости, считал, что он этот вопрос решил. В его работах я этого решения найти не смог. Но нет никакого сомнения: он был убежден, что он это сделал и внес тем самым огромный вклад не только в атомную физику, но и в эпистемологию, и в философию, и в человеческое самосознание в целом». «Совершенно непонятными» остались для Белла и работы Гейзенберга. Проблема измерения, очевидно, была серьезным вопросом, но в рамках копенгагенской интерпретации он считался тривиальным. Белл добивался строгости и честности, но на свои глубокие вопросы получал только какие-то малосущественные отговорки.

Затем Белл познакомился с доказательством фон Неймана – точнее, поскольку немецкого он не знал, с его изложением, сделанным Максом Борном. «На меня произвело глубокое впечатление, что кто-то – а именно фон Нейман – на самом деле доказал, что квантовую механику нельзя интерпретировать никаким другим образом», – рассказывал Белл. Он двинулся дальше. «Я очень рисковал тем, что раз уж я узнал об этих вопросах, то больше не смогу от них отвязаться <…> И я стал нарочно стараться о них не думать, – вспоминал он. – У меня появилось чувство, что если я так рано начну в них погружаться, то выбраться из этой трясины мне уже не удастся».

После окончания университета Куинс Белл нашел работу в Научно-исследовательском центре атомной энергии в Харуэлле, в Англии. Здесь он занимался разработкой ядерных реакторов с Клаусом Фуксом, ветераном Манхэттенского проекта. Но спустя несколько месяцев после прихода Белла Фукс сознался в том, что выдавал атомные секреты Советам. Белла перевели в отдел ускорителей. Там он познакомился с физиком Мэри Росс, своей будущей женой. Именно работая с Мэри в Харуэлле в 1952 году, Джон и наткнулся на незадолго до этого опубликованные статьи Бома о волне-пилоте.

Рис. 7.1. Джон Белл в Харуэлле, около 1952 года

Белл был поражен ледяным приемом, оказанным идеям Бома. «На протяжении двадцати пяти лет люди говорили, что альтернатива копенгагенской интерпретации невозможна. А после того как Бом нашел ее, некоторые из тех же людей совершили фантастический кульбит – объявили, что это тривиально». Прочтя статьи Бома, Белл тут же понял, что доказательство фон Неймана неверно. Но оно все еще не было опубликовано на английском языке. В Харуэлле Белл нашел коллегу, говорящего по-немецки, Франца Мандля. «Франц… пересказал мне кое-что из того, что писал фон Нейман, – вспоминал позже Белл. – Я уже тогда почувствовал, что понимаю, в чем заключается несообразность аксиоматики фон Неймана».

Но доказательство фон Неймана оставалось недоступным по-английски еще три года, а когда его наконец опубликовали на этом языке, Белл уже начал писать докторскую диссертацию на совершенно другую тему. Когда Белл поступил в аспирантуру, его научный руководитель Рудольф Пайерлс попросил его сделать доклад на одну из тем, которыми Белл в последнее время занимался, и Белл предложил на выбор рассказ о физике ускорителей или о квантовых интерпретациях. Пайерлс решительно предпочел ускорители. Белл подчинился, и на протяжении последующих нескольких лет ему больше не пришлось сталкиваться с вопросом о значении квантовой физики.

Однажды в ЦЕРНе (Европейском центре ядерных исследований в Женеве, в Швейцарии, где теперь работает знаменитый Большой адронный коллайдер) Белл встретился с самим Бором. Бор был в числе многих знаменитостей, приехавших на торжественное открытие этого исследовательского центра, а Белл и его жена только что приступили здесь к работе. Белл случайно оказался с Бором в лифте. Ему хотелось заговорить с живой легендой, но он не знал, с чего начать. «У меня недостало храбрости сказать: “Я думаю, что ваша копенгагенская интерпретация – фуфло”, – вспоминал он позже. – Ну и потом, поездка оказалась недолгой. Вот если бы лифт застрял между этажами, это могло бы изменить мою жизнь! Не знаю, правда, в какую сторону».

Когда три года спустя Беллы приехали в Калифорнию в творческий отпуск, Джон решил воспользоваться тем, что ему больше не надо было заниматься ежедневной рутинной работой в ЦЕРНе, и разобраться наконец, в чем же именно ошибся фон Нейман. Ему непременно хотелось завершить свой давний спор с Яухом. И он обнаружил, что легендарное доказательство фон Неймана, к которому постоянно апеллируют для защиты от всяческой квантовой ереси, на деле вообще едва ли может считаться доказательством чего бы то ни было! «Доказательство фон Неймана, если вникнуть в его суть, разваливается на глазах! – заявил Белл. – Оно построено на песке. Оно не просто ошибочно – оно бессмысленно (silly)!» Оказалось, великий Джон фон Нейман просто-напросто сделал элементарную ошибку – в своем доказательстве он исходил из предположений, которые были полностью безосновательны. «Когда вы переводите предположения фон Неймана на язык физических понятий, получается чепуха <…>. Доказательство фон Неймана не только неверно – оно просто глупо!»

Но Белл не только показал, что фон Нейман и Яух ошибались, – он построил новое доказательство вместо прежних. Принято было считать, что доказательство фон Неймана и другие построения того же типа (в том числе «усиленное» доказательство Яуха и доказательство Эндрю Глизона, о котором Яух когда-то рассказывал Беллу) исключали возможность любой интерпретации квантовой физики, в которой используются так называемые скрытые переменные. Такие интерпретации приписывают квантовым объектам определенные положения или другие свойства еще до того, как эти объекты наблюдаются, даже если эти свойства нельзя вычислить из теории. Математический аппарат квантовой физики эти свойства не описывает – он их как бы «не видит», откуда и происходит термин «скрытые переменные». Ярким примером такой теории как раз и является основанная на идее волны-пилота квантовая интерпретация Бома: в квантовом мире Бома частица всегда обладает определенным положением, хотя эти положения и остаются в основном скрытыми от глаз и не могут быть вычислены из уравнения Шрёдингера. Из доказательств фон Неймана, Яуха и Глизона вытекает, что схемы такого типа невозможны, – но Белл прекрасно знал, что волна-пилот Бома очевидным образом работает. Что-то здесь было не так, и Беллу казалось, он понимал, что именно. Он скрупулезно разделил на составные части доказательства, не содержавшие скрытых переменных, вдумчиво анализируя их элементы, пока не наткнулся на один из них, развалившийся пополам, – на ничем не обоснованное предположение в фундаменте логического построения. Перевернув это предположение с ног на голову, Белл показал, что пресловутые «доказательства без скрытых переменных» все как одно доказывали нечто совершенно иное, нечто, чего создатели этих доказательств вовсе не предполагали доказать или что они не вполне понимали. В частности, Белл обнаружил, что теория, содержащая скрытые переменные, могла обойти ловушки, расставленные этими доказательствами, если обладала одним довольно необычным свойством, позже названным контекстуальностью.

Контекстуальность означает, что исход измерения квантовой системы зависит от других вещей, которые вы измеряете в этой системе в то же самое время. Другими словами, если вы измеряете некоторое свойство объекта, исход вашего измерения может зависеть от того, какие другие характеристики этого объекта вы измеряете одновременно с этим. В контекстуальном мире, если вы измеряете энергию нейтрона одновременно с его импульсом, вы получите некоторое значение энергии нейтрона, но если вы измерили эту энергию одновременно с его положением, вы, возможно, получили совершенно другое ее значение просто из-за изменения контекста, в котором вы производили ваше измерение.

Чтобы получить более ясное представление о контекстуальности, забудем на время о нейтронах и поговорим лучше о колесе рулетки. Представьте, что ваша подруга Фло находится в казино, неподалеку от рулетки, а вы говорите с ней по телефону. Самого колеса вы не видите, но можете задавать ей вопросы о том, где остановился шарик рулетки после каждого броска. Вы можете спрашивать, выпал ли он на чет или нечет, на большие или малые числа, на красное или черное. (Рулетка устроена так, что половина номеров красная, а половина черная, при этом красной является половина как «малых чисел», от 1 до 18, так и «больших», от 19 до 36, и как половина четных, так и половина нечетных, а вторые половины, соответственно, черные, рис. 7.2.) Однако Фло почему-то не очень охотно сообщает вам, что происходит в казино: при каждом пуске колеса она отвечает только на два из трех ваших вопросов. В обычной ситуации это обстоятельство не имеет значения: что бы Фло вам ни сообщала, шарик все равно останавливается на какой-либо конкретной цифре. А следовательно, несмотря на то что реальное его состояние от вас скрыто, как только он останавливается, вы тут же получаете ответы на все три ваших вопроса. Если шарик остановился на цифре 34, значит, вы знаете, что он выпал на «большое», «красное» и «четное» число, хотя Фло ответила только на два из трех вопросов.

Но если колесо рулетки контекстуально, все происходит по-другому. Теперь ответ на вопрос «Выпал ли шарик на красное?» зависит от того, что вы еще спрашивали одновременно с этим. Допустим, после запуска колеса вы спросили, выпал ли шарик на красное и выпал ли он на чет. Оказалось, что на оба эти вопроса ответ положительный. Но если бы при том же запуске колеса вы задали другие вопросы – скажем, если бы вы спросили, выпал ли шарик на красное и выпал ли он на большое – тогда ответ на оба вопроса оказался бы отрицательным. Каким-то образом ответ на вопрос «Выпал ли шарик на красное?» оказывается зависящим от того, какой другой вопрос вы при этом задаете! Это и есть контекстуальность: ответ на вопрос зависит от контекста, создаваемого сопутствующими вопросами, задаваемыми в то же самое время. Разрушая доказательства, не содержащие скрытых переменных, Белл одновременно продемонстрировал, что квантовая физика описывает именно контекстуальный мир.

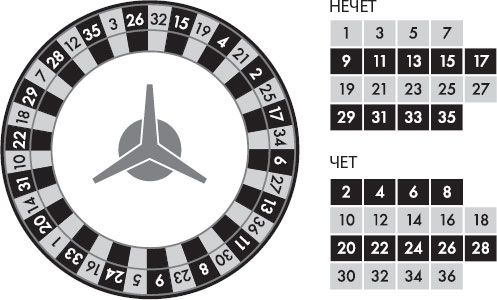
Рис. 7.2. Колесо идеальной рулетки. Числа поровну распределены между категориями «большие – малые», «красные – черные» и «четные – нечетные»; поля 0 и 00 отсутствуют

На первый взгляд может показаться, что контекстуальная природа квантовой физики согласуется с копенгагенской интерпретацией или по крайней мере ей не противоречит. Если ответы на вопросы зависят от других одновременно задаваемых вопросов, разве это не означает, что мы не можем получить ответ на вопрос до тех пор, пока не зададим его? В конце концов, если квантовый мир контекстуален, он не может быть похож на колесо рулетки – шарик не может выпасть на конкретный номер и пассивно дожидаться, когда мы на него посмотрим, так как свойства этого номера зависят от того, что мы спрашиваем о нем. Цвет номера рулетки не изменяется, когда мы спрашиваем, четный он или нечетный; номер 34 останется красным независимо от того, задаем ли мы об этом какие-либо вопросы. А значит, в квантовом мире не может быть ни рулетки, ни шарика – до тех пор, пока мы не примемся их искать. Как сказал Паскаль Йордан, «Мы сами производим результаты своих измерений».

Но, невзирая на всю привлекательность этих по-копенгагенски звучащих аргументов, Белл с ловкостью дзюдоиста опроверг их, процитировав самого Бора. В той же статье, в которой Белл объявил контекстуальность главной особенностью квантового мира, он также указал, что эта особенность не должна никого удивлять: ведь, по словам Бора, невозможно провести «никакого резкого различия между поведением атомных объектов и их взаимодействием с измерительными устройствами». Вы не можете заглянуть в квантовый мир, не изменив его, но это вовсе не означает, что квантового мира не существовало, пока вы в него не заглянули. Совсем наоборот: если бы его не было, вы не смогли бы изменить его в процессе наблюдения! И контекстуальное колесо рулетки может существовать – просто положение шарика будет изменяться, когда вы смотрите на него разными способами, ведь вы не можете отделить поведение шарика от его взаимодействия с вами в процессе наблюдения. Это не значит, что шарика не существует или что он не обладает никаким местоположением, пока вы на него не посмотрите; это означает, что шарик просто-напросто очень прыгучий и чувствительный, что он начинает бешено метаться даже от малейшего воздействия. Именно так и ведут себя скрытые переменные в построенной на базе волн-пилотов интерпретации Бома. Согласно Бому, частица всегда обладает определенным местоположением – но это положение может резко изменяться благодаря малым возмущениям и изменениям в экспериментальных схемах. Стоит вам, находясь в бомовском квантовом мире, задать электрону немного отличную от первоначальной серию вопросов, и вы получите совершенно не похожую на первоначальную серию ответов – но сам электрон все это время занимает вполне определенное положение. И так как теория Бома контекстуальна, она остается неуязвимой для всех доказательств, которые пытаются ее опровергнуть. «Все, что доказывают эти доказательства, – заключает Белл, – это недостаток воображения».

Несмотря на построенную им убедительную демонстрацию того, что теория Бома не является невозможной, Белл все-таки был обеспокоен наиболее странной особенностью концепции волны-пилота: ее «скрытой нелокальностью». «В теории Бома происходили ужасные вещи, – писал Белл. – Например, траектории частиц мгновенно изменялись, как только в какой-то точке Вселенной кто-нибудь двигал магнит». Была ли нелокальность теории Бома существенной особенностью квантовой физики? Белл поставил этот вопрос в заключительной части своей статьи, развенчивающей доказательство фон Неймана, и оставил его без ответа, указывая тем самым возможное направление дальнейшей работы.

Долгое время поставленный Беллом вопрос о нелокальности оставался вне поля зрения физиков: вследствие ряда канцелярских ошибок его статья о доказательстве фон Неймана два года пролежала в столе у редактора. Но Белл не мог махнуть на этот вопрос рукой – он хотел найти ответ немедленно. В этом и заключался его новый проект. «Я, конечно, знал, что мысленный эксперимент Эйнштейна – Подольского – Розена сыграл критическую роль [в выявлении нелокальности], так как в нем возникали мгновенные корреляции на расстоянии, – вспоминал позже Белл. – Поэтому я в явном виде поставил следующую задачу: построить простую модификацию опыта Эйнштейна – Подольского – Розена, для которой можно было бы создать модель, одновременно не нарушающую квантово-механической картины и сохраняющую полную локальность».

В этой работе Белл использовал упрощенную схему эксперимента ЭПР, предложенную Бомом в учебнике, который он написал непосредственно перед тем, как разработал свою концепцию волны-пилота. Эта версия опыта ЭПР позволила Беллу намного упростить выстроенную им мысленную конструкцию. Вместо сталкивающихся и затем разлетающихся в разные стороны двух частиц с запутанным импульсом в построенной Бомом версии опыта ЭПР участвовали фотоны с запутанной поляризацией.

Поляризация – волновое свойство света. Свет является электромагнитной волной, а его поляризация – это преимущественная плоскость колебаний этой волны. Но для наших целей важно только то, что явление поляризации связано с пространственным направлением: мы можем представить себе поляризацию в виде маленькой стрелки, привязанной к каждому фотону и указывающей то или иное направление. Однако все это не так уж просто. Во-первых, мы не можем сказать, куда именно направлена стрелка поляризации фотона. Все, что мы можем сделать, – это измерить поляризацию фотона вдоль некоторой заданной оси в некоторый момент времени. Сделать это можно несколько косвенным путем: ставя на пути фотона поляризатор (линзу из поляроидных солнечных очков). Когда фотон попадает в поляризатор, он либо проходит сквозь него, либо поглощается; и чем ближе стрелка поляризации фотона к направлению оси поляризатора, тем выше у фотона вероятность пройти сквозь поляризатор.

В бомовской версии ЭПР два фотона с запутанной поляризацией вылетают из одного источника в противоположных направлениях к двум поляризаторам. Поляризаторы установлены так, чтобы измерять поляризацию вдоль одной и той же оси. Так как фотоны обладают запутанной поляризацией, то, когда они попадают в поляризаторы, с ними всегда происходит одно и то же – оба они либо блокируются поляризаторами, либо проходят сквозь них. При этом неважно, по какой оси установлены поляризаторы: коль скоро оси поляризаторов согласованы, запутанные фотоны нашей пары всегда будут вести себя одинаково на каждом из них. И, главное, не имеет значения, насколько далеко друг от друга поляризаторы установлены: независимо от расстояния между ними оба фотона либо пройдут сквозь них, либо будут поглощены.

Именно это и должно происходить по законам квантовой физики. Два запутанных фотона описываются одной и той же волновой функцией, что и гарантирует их неизменно одинаковое поведение при встрече с двумя поляризаторами с согласованными осями. Что именно они делают – поглощаются или проходят через поляризаторы, – волновая функция не определяет, но делать они должны непременно одно и то же.

Тут наконец выходит на свет сформулированный Эйнштейном принудительный выбор, который, как он опасался, не был ясно очерчен в статье ЭПР. Если мы предполагаем, что в природе действует принцип локальности, то единственным объяснением идеально синхронизированного на большом расстоянии танца запутанных фотонов будет то, что сценарий этого танца запрограммирован заранее, что фотоны сговорились о нем до того, как вылетели из своего общего источника. Но волновая функция, которая объединяет запутанные фотоны, ничего не сообщает нам ни о каком предварительном сговоре. Она только гарантирует, что фотоны, встретившись с одинаково настроенными поляризаторами, станут всегда вести себя одинаково, будут идеально скоррелированы. Следовательно, если природа придерживается принципа близкодействия, тогда кроме волновой функции должно быть еще что-то – должны быть скрытые переменные. Либо квантовая физика неполна, либо природа нелокальна. Нельзя совместить близкодействие и полноту квантовой физики. Это и есть вынужденный выбор Эйнштейна, в этом суть парадокса ЭПР.

Белл принялся с разных сторон анализировать мысленный эксперимент ЭПР – Бома, пытаясь построить модель, в которой сохранялись бы все результаты, предсказываемые квантовой физикой, и при этом полностью локальную, то есть построенную на принципе близкодействия. «Но как я ни старался, ничего не выходило, – рассказывал Белл. – И мне начало казаться, что, скорее всего, этого сделать не удастся. Тогда я сконструировал “доказательство невозможности”».

Эйнштейн когда-то доказал, что квантовая физика должна выбирать между локальностью и полнотой. Построенное Беллом «доказательство невозможности» показало, что в действительности выбор делается между локальностью и корректностью. Исходя из предположения о том, что в природе действует принцип локальности, Белл вывел некое неравенство, математическое условие, которому должна удовлетворять любая локальная теория. Затем Белл искусно видоизменил бомовскую версию мысленного эксперимента ЭПР, создав ситуацию, в которой предсказания квантовой физики это неравенство нарушают.

Цель логической эквилибристики Белла состояла в том, чтобы продемонстрировать несовершенство предсказаний квантовой физики, а не их совершенство. В конце концов, идеальные корреляции, имеющие место в мысленном эксперименте ЭПР – Бома, легко сочетаются с принципом локальности – фотоны могут получать «секретные инструкции» о своем дальнейшем поведении в точке их совместного рождения. Но если вы поворачиваете ось одного из ваших поляризаторов, квантовая физика предсказывает, что пары запутанных фотонов, поступающие на вход этих поляризаторов, не будут больше вести себя всегда в точности одинаковым образом. И Белл показал, что эти неидеальные корреляции, предсказываемые квантовой физикой, все же слишком сильны, чтобы любая локальная теория взаимодействий могла их объяснить. Так что либо предсказания квантовой физики неверны и природа может быть локальной, либо квантовая физика права и «это жуткое дальнодействие» является реальностью. Белл открыл некую исключительно глубокую и контринтуитивную истину нашего мира.

К тому же Белл показал, что возможна экспериментальная проверка, которая позволила бы выбрать между этими двумя вариантами. Все, что для этого требуется, – построить и выполнить модифицированную Беллом версию мысленного эксперимента ЭПР или какого-либо другого эксперимента, построенного на взаимодействии запутанных частиц. Если результат этого опыта покажет, что неравенство Белла нарушается, квантовая физика оправдана, но природа нелокальна; если неравенство выполняется, то квантовая физика ошибается, но природа может быть построена на близкодействии. Таким образом, «доказательство невозможности» Белла вывело вопрос о нелокальности из сферы обсуждений и сделало его экспериментальной задачей. Это доказательство, известное теперь как теорема Белла, справедливо названо «глубочайшим научным открытием».

Полученный Беллом результат оказался неожиданным и поставил новые проблемы. Близкодействие – основное предположение физики, да и вообще всей науки. Если отказаться от принципа локальности, невозможно вообще говорить о каких-либо управляемых экспериментах – как бы тщательно вы ни контролировали область непосредственного окружения вашего опыта, всегда остается возможность удаленного мгновенного воздействия на его результат. Именно по этой причине Эйнштейн, в частности, подчеркивал, что локальность должна быть основным принципом науки, отказаться от которого возможно только под давлением абсолютно непреложной необходимости. «Без такого допущения о взаимно независимом существовании пространственно удаленных предметов, допущения, которое основывается на ежедневном опыте мышления, физическое мышление в привычном для нас смысле было бы невозможно, – писал он. – Без этой идеи полного разделения никто также не смог бы понять, как можно формулировать и экспериментально тестировать физические законы <…> Полная отмена этого фундаментального принципа сделала бы невозможной идею существования (квази-) замкнутых систем, а следовательно, и установление эмпирически проверяемых законов в привычном для нас смысле».

Даже если отвлечься от философских взглядов Эйнштейна, его научные результаты не оставляли сомнения в том, что локальность – ключевое свойство нашего мира. Согласно эйнштейновской специальной теории относительности, физические объекты невозможно заставить двигаться со скоростью, равной скорости света или превышающей ее, – иначе мы получим целый букет парадоксов с участием бесконечной энергии. Можно было бы попробовать обойти этот запрет, отыскав нечто, уже движущееся быстрее света, но таких объектов никто никогда не обнаруживал. И действительно, физика релятивистских частиц утверждает, что такие объекты были бы совершенно неустойчивы. Им не позволяли бы существовать их собственные парадоксы, связанные с бесконечной энергией. И даже если бы вы каким-то образом обошли эти проблемы и сумели отправить сигнал со скоростью, превышающей световую, вы все равно рисковали бы получить парадокс: согласно теории относительности, сама посылка сверхсветового сигнала немедленно сделала бы возможным построение «тахионного антителефона», с помощью которого можно было бы посылать сообщения в прошлое.

Но из теоремы Белла вовсе не следует, что мы можем звонить сами себе во вчерашний день или послать в 1955 год новейший спортивный автомобиль. Белл и другие исследователи позже доказали, что квантовую запутанность невозможно использовать для посылки сверхсветовых сигналов. А особый вид нелокальности, свойственный запутанным частицам, вещь тонкая и сложная, и проявляется она только в столь специфических условиях, что никак не может создать экзистенциальной угрозы самой науке, чего так боялся Эйнштейн. Но факт остается фактом – в мире, в котором специальная теория относительности легко прошла все устроенные ею проверки, – в мире, который оказывается строго локальным, – призрак нелокальности, вызванный теоремой Белла, вызывает глубокое беспокойство. Если квантовые предсказания исхода опыта Белла верны и неравенство Белла не выполняется, значит что-то все же нелокально, значит локальность всего только иллюзия. А это предполагает необходимость радикального пересмотра нашей концепции пространства и времени, пересмотра, далеко выходящего за пределы эйнштейновской относительности. Любая картина мира, в котором допускается нарушение неравенства Белла, была бы поистине странной.

Как же Беллу удалось получить из своих рассуждений столь неожиданные, далеко идущие и всеобъемлющие следствия? Чтобы вполне понять построенное им доказательство, нам понадобится нечто большее, чем колесо рулетки, – нам потребуется целое казино. (Читатели, которым неинтересно углубляться в детали доказательства Белла, вполне могут пропустить весь следующий раздел – это никак не скажется на понимании остальной части нашей книги. Но если вы все же отважно последуете за нами и попытаетесь разобраться в аргументации этого раздела, вы, как мы надеемся, достигнете более глубокого понимания того, что сделал Джон Белл.)

В маленьком городке Бельвиль, в глухом северо-восточном уголке штата Калифорния, открывается новое казино. О его владельце Ронни по кличке Медведь поговаривают, что он связан с преступным миром. Фатима и Джиллиан, инспекторы калифорнийского Игорного Бюро, направляются в Бельвиль, чтобы, пока казино не открылось, все как следует проверить. Ведь Ронни наверняка что-то задумал.

В новом казино Ронни установлена сверхсложная рулетка – возможно, специально для того, чтобы произвести впечатление на инспекторов. В центре зала помещается громадная машина с желобком для шарика; желобок тянется через весь зал, от одного стола с фишками до другого. У каждого из двух столов – по три колеса рулетки, каждое со своим вращающимся полем и общим вертящимся стрелочным указателем (рис. 7.3).

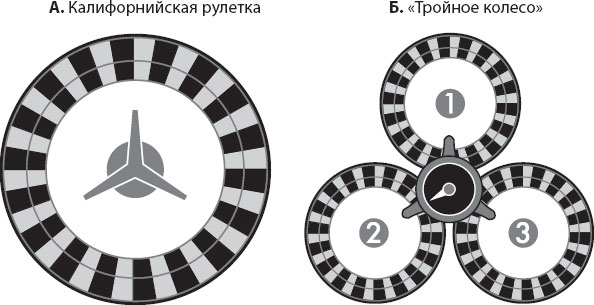
Рис. 7.3. А. Калифорнийская рулетка. Б. В казино у Ронни: «тройное колесо» с закручивающимся указателем в центре

По законам штата Калифорния, на полях рулеточных колес только перемежающиеся красные и черные квадраты – колеса с цифрами здесь запрещены. Как только Фатима и Джиллиан усаживаются каждый за свой стол, Ронни нажимает кнопку машины, и в желобок выкатывается по шарику с каждой стороны – каждый из них катится к своему столу. Пока они катятся, инспекторы закручивают центральный указатель, шарик с каждой стороны автоматически скатывается на то из трех колес, на которое указывает его стрелка, и в конце концов останавливается на красном или черном поле (рис. 7.4).

Рис. 7.4. Столы рулетки в казино Ронни Медведя в Бельвиле

Чтобы тщательно проверить случайный характер вращения колес, Джиллиан и Фатима проделывают эту процедуру много раз подряд и подробно записывают исход каждого пуска шариков: на какое колесо указала стрелка, и на поле какого цвета выпал шарик. После нескольких десятков запусков инспекторы возвращаются к себе, чтобы сравнить записи. Они обнаруживают, что на обоих столах колеса крутятся будто совершенно случайным образом – красное и черное выпадают примерно поровну. Но между записями Фатимы и Джиллиан обнаруживается странная корреляция: каждый раз, когда стрелки указателей на обоих столах указывают на один и тот же номер колеса, оба шарика останавливаются на одинаковых цветах. Например, на восемьдесят седьмой попытке обе стрелки показали на колесо номер 2 – и оба шарика выпали на красный (рис. 7.5). Инспекторы заключают, что гигантская машина так программирует шарики, чтобы при выходе на колеса с одинаковыми номерами они обязательно выпадали на одинаковые цвета.

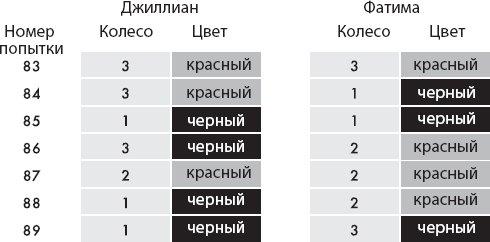
Рис. 7.5. Сравнение отрывков из записей Джиллиан и Фатимы

Однако затем Фатима замечает еще одну закономерность: когда шарики попадают на колеса с разными номерами, они оказываются на полях с одинаковым цветом только в 25 процентах случаев. Фатима считает, что это противоречит предположению о программировании шариков. Чтобы доказать это, она выписывает все восемь различных возможных вариантов инструкций, которым могут подчиняться шарики рулетки (рис. 7.6).

По первой из этих инструкций, «красный – красный – красный», шарик всегда приходит на красное поле, независимо от номера колеса, на которое он попадает. По второй инструкции, «красный – красный – черный», шарик останавливается на красном поле, если попадает на колеса 1 или 2, но если он попадает на колесо 3, то останавливается на черном поле. Составленный Фатимой список включает все восемь возможных вариантов поведения шарика, и на его основании она заключает, что, какой бы из этих вариантов ни реализовался, в случае, если номера колес не совпадают, цвета полей, на которые выпадает шарик, на ее стороне и на стороне Джиллиан должны совпадать более чем в 25 процентах случаев.

• Если оба шарика следуют инструкции «красный – красный – красный» или «черный – черный – черный», цвета полей, на которые они выпадают, совпадут в 100 процентах случаев, даже когда они приходят на колеса с разными номерами.

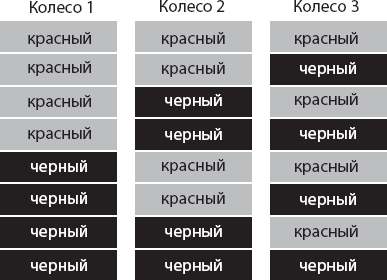
Рис. 7.6. Полный набор «инструкций» поведения шарика рулетки

• Если оба шарика следуют одной из остальных инструкций, то, когда у Фатимы и Джиллиан шарики оказываются на колесах с разными номерами, шарики должны выпасть на один цвет в одной трети (33 процента) случаев. Допустим, что они следуют инструкции «черный – красный – красный». Тогда Фатима и Джиллиан получат поля разных цветов, если шарики придут на комбинации колес 1–2, 2–1, 1–3 или 3–1. Но шарики выпадут на один цвет при комбинациях колес 2–3 или 3–2 – два варианта из шести возможных, то есть одна треть. Точно такая же картина будет наблюдаться, и если шарики станут следовать другим инструкциям (отличным от «черный – черный – черный» и «красный – красный – красный»).

Следовательно, когда номера колес со стороны Фатимы и Джиллиан не совпадают, одинаковый цвет на них должен выпадать по крайней мере в 33 процентах всех случаев – инструкций, для которых такие совпадения будут происходить реже, не существует. И все же, согласно записям, совпадения цветов в этих ситуациях происходят только в 25 процентах случаев! Это заставляет инспекторов заключить, что шарики рулетки не получают одинаковых инструкций. Но ведь шарики рулетки всегда выпадают на одинаковые цвета, когда номера колес со стороны Джиллиан и Фатимы совпадают! Ясно, что между ними существует какая-то координация – ведь именно это обстоятельство и вызвало у инспекторов подозрения, что при запуске шарикам сообщаются какие-то «инструкции». Этот парадокс можно объяснить только одним способом: шарики рулетки обмениваются сигналами уже после того, как они узнают, на какие колеса они должны попасть.

Предыдущий раздел представляет собой слегка видоизмененное доказательство теоремы Белла. Пары шариков рулетки – это пары фотонов с запутанной поляризацией. Колеса рулетки – поляризаторы, измеряющие поляризацию по трем различным направлениям, случайно выбранным, пока фотоны летят к поляризаторам. А суть теоремы Белла – это тот самый вывод, к которому пришла Фатима. Если шарики вашей рулетки действительно ведут себя так, значит происходит нечто странное, и эту странность нельзя объяснить предположением, что шарики рулетки получают тайные инструкции (то бишь скрытые переменные), которые они несут с собой с момента своего разделения. А поскольку запутанные фотоны действительно ведут себя именно так, значит, нечто очень странное должно происходить в квантовой физике. Но что же именно доказал Белл? Чтобы это понять, посмотрим более пристально на то, что произошло в казино Ронни.

Мы начали с предположения, что шарики рулетки не могут волшебным образом мгновенно сообщаться друг с другом, находясь друг от друга на большом расстоянии (хотя до сих пор мы ни разу не констатировали этого в явном виде). Другими словами, мы начали с предположения о локальности. Это предположение привело нас к идее, что шарики рулетки должны получать скрытые инструкции – это был единственный способ объяснить постоянное согласование цветов, на которые выпадали шарики, когда номера колес у Джиллиан и Фатимы совпадали. Но странные корреляции исходов в тех случаях, когда номера колес у Джиллиан и Фатимы не совпадали, исключали возможность существования скрытых переменных. Следовательно, что-то не так было с самим нашим предположением: локальность должна нарушаться. В казино Ронни, конечно, могло случиться всякое – шарики рулетки могли поддерживать связь хоть по радио. Но в реальных экспериментах «шариками рулетки» были летящие со скоростью света фотоны, а «колесами» – поляризаторы, и они могли быть удалены друг от друга на очень большие расстояния, в некоторых экспериментах – на сотни километров. Никакой сигнал, посланный со скоростью света одним из фотонов после того, как он достиг поляризатора, не мог бы успеть достичь другого фотона и повлиять на его поведение прежде, чем тот достигнет своего поляризатора. Короче говоря, результаты реальных экспериментов с запутанными фотонами означают, что существует некое воздействие, распространяющееся быстрее света. Запутанность – не просто артефакт математического аппарата квантовой физики; это реальное явление, действительно существующая мгновенная связь между объектами, удаленными друг от друга на большое расстояние.

Это поразительный результат. Как это может быть правдой? Каким может быть мир, в котором это возможно? Самый очевидный ответ: этот мир нелокален. Основанная на идее волны-пилота бомовская интерпретация квантовой физики с теоремой Белла прекрасно согласуется – ведь теория Бома явно нелокальна. Это превращает одну из видимых слабостей теории волны-пилота – мгновенную связь между частицами, разделенными огромными расстояниями, – в ее силу. Теорема Белла дает веские основания предполагать, что квантовая физика должна быть нелокальной; теория волны-пилота делает это странное квантовое поведение столь очевидным, что его уже невозможно игнорировать.

Но цена, которой достается нелокальность, высока. Теория относительности – одно из наиболее прочных и фундаментальных оснований современной физики; нелокальность поставила бы ее под сомнение. Может, есть какой-нибудь способ обойти теорему Белла? Неужели принцип близкодействия – единственно возможное допущение? Ну да, Джиллиан и Фатима действительно были уверены, что их записи проведенных в казино испытаний рулетки полностью отражали все, что там происходило. И, в частности, они полагали, что при каждом раскручивании колеса рулетки был только один исход пуска каждого шарика – тот, который они записали. А если каким-то образом при каждом раскручивании колеса и пуске шарика исходов было больше одного? Тогда получается, что каждый раз, когда фотон попадает в поляризатор, доказательство Белла рушится. А именно это и происходит в многомировой интерпретации Эверетта. Согласно Эверетту, каждое раскручивание колеса рулетки, разветвляясь вместе с универсальной волновой функцией на множество миров, приводит к обоим возможным исходам, при которых шарик выпадает и на красное, и на черное. Таким образом, теорема Белла заставляет полагать, что если мы не готовы пожертвовать близкодействием, то наиболее странная часть схемы Эверетта, возможно, необходимое свойство мира.

Итак, нам предстоит выбор одного из двух возможных предположений: локальность или единственность Вселенной. Одно из них должно быть неверным, ведь неравенство Белла экспериментом не подтверждается. Значит ли это, что теорема Белла ставит нас перед этим выбором? Или здесь есть еще одна, третья таинственная возможность? Возможно, указатель, при помощи которого выбирается одно из трех колес, действует не вполне случайно, и шарики рулетки заранее «знают», на какое из трех колес они попадут. Такой «сговор» между колесами и шариками мог бы объяснить странный результат, к которому пришли Фатима и Джиллиан. Попробуем перевести это на язык реальной физики: может ли существовать сговор между фотонами и поляризаторами? Такое предположение звучит, мягко говоря, нереально. Разве не правда, что экспериментатор каждый раз произвольно выбирает используемый поляризатор? Если так, то как фотоны могут знать наперед, что он выберет? Мы привыкли считать, что свободно выбираем условия наших экспериментов, но даже если это иллюзия, то идея, что фотоны каким-то образом предвосхищают внутри себя все наши действия, плохо укладывается в сознании. Технически, однако, такой «сверхдетерминизм» может быть логически возможным способом избежать требований теоремы Белла. Горсточка теоретиков действительно пытается работать в этом направлении (хотя есть опасения, как бы признание возможности такого «сговора» не сделало бы невозможным занятие наукой как таковой).

Можно ли придумать что-нибудь еще? Существуют ли другие способы обойти эту замечательную теорему Белла? Есть много книг и статей, в которых утверждается, что в доказательстве Белла есть и еще одно допущение – допущение скрытых переменных. Стоит только исключить предположение, что шарики рулетки вообще способны нести какие-либо скрытые инструкции, говорят нам сторонники этой позиции, и теорема Белла тут же потеряет силу. Но это не так. Мы и не предполагали, что шарики рулетки несут скрытые инструкции, – по крайней мере, в начале нашего доказательства. Мы предположили всего лишь существование локальности, и это неизбежно привело нас к выводу, что у шариков должны быть какие-то инструкции, – должны же мы были как-то объяснить идеальное соответствие между результатами Джиллиан и Фатимы, когда они обе использовали колеса с одним и тем же номером. Вам слышится что-то знакомое? Конечно, это же в чистом виде аргументы ЭПР. Если пары шариков всегда выпадают на одинаковые цвета, то они либо выполняют одинаковые инструкции, полученные ими при запуске, либо сразу же по достижении ими своих целей каким-то образом сообщаются друг с другом со скоростью, превышающей скорость света. Здесь нет никаких предположений о скрытых переменных – всего лишь предположение о локальности, а вводить скрытые переменные вынуждает нас поведение шариков. «Самое трудное – это объяснить, что скрытые переменные не являются исходной предпосылкой анализа, – жаловался Белл спустя пятнадцать лет после первой публикации своей теоремы. – Моя первая статья на эту тему (о теореме Белла) начинается с итогового перечисления аргументов ЭПР, начиная с локальности и заканчивая детерминистскими скрытыми переменными. Но комментаторы почти всегда отмечают, что статья начинается с введения детерминистических скрытых переменных».

Еще одно связанное с этим утверждение заключается в том, что теорема Белла предполагает существование некоторого особого вида реальности. Это утверждение особенно популярно среди сторонников копенгагенской интерпретации. Если вы не предполагаете, что у квантового мира есть реальные свойства – или что какой-то квантовый мир вообще существует, – тогда, говорят они, теорема Белла не работает. Но это тоже неверно. Здесь все дело в выражении «некоторый особый вид реальности». Что, собственно, понимается под «реальностью»? По мнению некоторых физиков, теорема Белла основывается на идее, что у квантовых объектов имеются вполне определенные свойства еще до всякого измерения и что это-то и подразумевается под «реальностью». Но, как уже было сказано выше, это просто-напросто неверно – в теореме Белла нет никаких предположений о наперед существующих свойствах частиц (то есть о скрытых переменных). Ее идея вытекает из предположения о локальности точно так же, как аргументация ЭПР. Другие заявляют, что форма реальности, предполагаемая теоремой Белла, сводится к все той же идее о существовании всего мира вне зависимости от наблюдений. Отрицание такого существования, говорят они, и составляет истинную суть копенгагенской интерпретации, и именно это позволяет этой интерпретации оставаться локальной, невзирая на искусно построенное доказательство Белла. Даже если оставить в стороне вводимый таким отрицанием в физику солипсизм – чьи именно наблюдения придают вещам реальность? Здесь возникает еще одна проблема. Ведь если отказаться от предположения, что реальность существует независимо от какой-либо формы наблюдения, обессмысливается сама идея близкодействия. Как может иметь какое-то значение разговор о воздействиях, передающихся от объекта к объекту из одного места в другое быстрее света, когда ни сами объекты, ни их положения вообще не существуют? Разрушение доказательства Белла путем отрицания реальности тут же неизбежно разрушает и концепцию локальности – пиррова победа антиреалистов, твердо решивших сохранить локальность в физике любой ценой. Сам Белл сказал об этом так: «Я не знаю ни одной концепции локальности, которая совмещается с квантовой механикой. Поэтому думаю, что от нелокальности нам не отделаться».

Даже само существование квантовой физики не является исходным предположением доказательства Белла. В конце концов, разве Фатима апеллировала к квантовой физике, когда объясняла невозможность случайного поведения шариков на рулетке Ронни? Теорема Белла – это утверждение, касающееся мира в целом, независимо от законов квантовой физики. Если мир ведет себя определенным образом – если шарики рулетки Ронни или запутанные фотоны подчиняются статистическим закономерностям, которые наблюдались в казино, – то значит либо локальность нарушается, либо в природе реализуется что-то вроде многомировой интерпретации (или, быть может, природа конспирологична и сверхдетерминистична). Единственный пункт в этой аргументации, в котором появляется квантовая физика, это когда в соответствии с математикой квантовой теории обнаруживается, что запутанные фотоны ведут себя так же, как и шарики в рулетке Ронни. Следовательно, если квантовая физика верна или, по крайней мере, если она верна для этой частной ситуации, нам придется пожертвовать локальностью или жизнью в единичной Вселенной (а может, и тем и другим).

Короче говоря, теорема Белла фактически оставляет всего три однозначные возможности: либо природа в каком-то отношении нелокальна, либо мы живем в ветвящейся системе множественных миров, несмотря на ряд очевидных свидетельств обратного, либо квантовая физика дает неверные предсказания в определенных экспериментальных ситуациях. Что бы из этого ни оказалось правдой, работа Белла представляет угрозу для копенгагенской интерпретации. И, возможно, из-за того, что теорема Белла противоречит этой широко распространенной мудрости, физики в течение длительного времени испытывали трудности в понимании истинного ее значения. По сути, недоразумения с ней начались еще до того, как она была опубликована.

Получив доказательство своей революционной теоремы, Белл находился в нерешительности – в какой научно-исследовательский журнал ее послать? Очевидным выбором казался главный физический журнал в мире, Physical Review, в котором на протяжении предшествовавших тридцати лет появились и статья ЭПР, и ответ на нее Бора, и работы Бома о волнах-пилотах. Авторитетнейший Physical Review читали все физики мира. Но публикация в нем стоила денег. Их обычно выделял институт, в котором работал автор статьи. Белл в SLAC был визитером и не хотел обременять расходами тех, кто оказывал ему гостеприимство, особенно когда речь шла о столь нетрадиционной работе. «Мне было неудобно просить их заплатить за мою статью», – объяснял он. Поэтому он отправил свою работу в новый и пока не имевший установившейся репутации журнал Physics («Физика»).

Журнал Physics – а точнее Physics Physique Fizika: Международный журнал для публикации избранных статей, заслуживающих особого внимания физиков всех специальностей – был журналом необычным. Его основали двое выдающихся специалистов в области физики твердого тела: Филипп Андерсон (в 1977 году он получит Нобелевскую премию) и Бернд Маттиас. Андерсон и Маттиас хотели, чтобы их журнал стал физической версией «журнала литературной и общей информации, таким как Harper’s» – в нем должны были появляться материалы изо всех областей физики, о чем и объявляло его полное название. В стиле Harper’s Андерсон и Маттиас не брали с авторов денег за публикации, а наоборот, выплачивали им гонорары, хотя и очень скромные. Белла такой вариант идеально устраивал. «Я решил, что, если пошлю свою работу в Physics, это будет прекрасным способом избежать неловкой ситуации».

Статья Белла произвела на Андерсона сильное впечатление – но не по той причине, на которую мог бы надеяться Белл. «Меня порадовала мысль о том, что эта работа, возможно, опровергает бомизм [sic], – вспоминал Андерсон, – и мне показалось, что в основном в ней все правильно». Забавно, что Андерсон, который в этом случае совместил роли редактора и рецензента, по-видимому, принял статью Белла к печати как раз потому, что по сути глубоко ошибся в понимании ее содержания.

Дело еще больше осложнилось тем, что журнал Physics Physique Fizika долго не просуществовал – после того как вышло несколько его номеров, Андерсон и Маттиас были вынуждены превратить его в традиционный журнал по физике твердого тела, а к 1968 году его и вовсе пришлось закрыть из-за трудностей с распространением и разногласий с издательством. Затерянная в забытых старых номерах малотиражного и больше не издающегося академического журнала, работа Белла долго оставалась почти полностью незамеченной – автор не получал абсолютно никаких откликов на нее на протяжении почти пяти лет после ее появления. Но те несколько человек, которые все же прочли ее, за нее ухватились. К середине 1970-х работа Белла вызвала в среде специалистов по квантовой физике полномасштабную смуту – впервые со времен дебатов между Бором и Эйнштейном копенгагенской интерпретации был брошен серьезный вызов, получивший широкий резонанс в физическом сообществе.

Но еще до того, как это случилось, – по сути, задолго до того, как Белл еще только начал обдумывать свою теорему, – началась совсем другая смута. Эта академическая война быстро переросла в революцию, опрокинувшую весь предшествовавший ей порядок и имевшую серьезнейшие последствия для оснований квантовой физики. Тем не менее эта революция ускользнула от внимания Джона Белла и большинства других физиков. Фактически самой физики она почти не касалась. Однако крах логического позитивизма и восхождение научного реализма радикально изменили философию науки и в конечном счете нанесли сокрушительный удар по самим основам копенгагенской интерпретации.