Книга: Лаборатория химических историй. От электрона до молекулярных машин
Назад: Получить больше, чем рассчитывал
Дальше: Глава 11 Всегда ли надо мыть посуду?
Можно обойтись без денежного выражения
Методика справедливого раздела может быть использована и при решении некоторых проблем, возникающих в научной практике. Возьмем для примера многостадийный органический синтез – например, получение уксусной кислоты CH3COOH из метана CH4. На самом деле уксусную кислоту никто так не синтезирует, в промышленности ее получают окислением бутана С4Н10 или взаимодействием метанола СН3ОН с монооксидом углерода СО. Однако выберем необычный способ синтеза, а заодно убедимся, что он осуществим.
Рассмотрим все стадии процесса. Вначале бромированием получаем из метана бромметан:
CH4 + Br2 = CH3Br + HBr
Затем проводим взаимодействие бромметана с металлическим магнием, который «встраивается» между углеродом и бромом. Образуется магнийорганическое соединение (реактив Гриньяра). Реакция проводится в диэтиловом эфире:
CH3Br + Mg = CH3MgBr
На следующей стадии полученный реактив Гриньяра взаимодействует с углекислым газом СО2, который «встраивается» между углеродом и магнием:
CH3MgBr + CO2 = CH3C(=O)OMgBr
Последняя стадия: при взаимодействии соединения, полученного на предыдущей стадии, с HBr, образуется уксусная кислота и побочный продукт MgBr2:
CH3C(=O)OMgBr + HBr = CH3COOH + MgBr2
Вся работа достаточно трудоемкая, поскольку, помимо проведения четырех основных стадий, необходимо предварительно очистить исходные соединения и растворители, а также отделить побочные продукты реакций.
Предположим, что получение большого количества конечного продукта будет оплачено. Общая стоимость работы для решения нашей задачи значения не имеет, и мы не будем ее рассматривать. Чтобы успеть все сделать к назначенному сроку, вы берете себе в помощники еще двух химиков. Опыт экспериментальной работы у всех троих одинаков, каждый сможет провести любую из показанных выше стадий. Поэтому все трое решили поделить заработанную сумму на три равные части. Теперь надо разделить объем работы также на три равные части.
Несмотря на то что мы решили обойтись без денежного выражения объема работы на каждой стадии, мы постараемся соблюсти принцип справедливого раздела. Сформулируем его несколько иначе – в сравнении с тем, который применялся при разделе наследства. Каждому химику нужно предоставить возможность выполнить объем работы меньший, чем одна треть (по его собственной оценке) общего объема. Объединим все участвующие в синтезе соединения, затем дадим каждому из участников независимо друг от друга провести деление всего объема работы на три равные части с помощью вертикальных черточек. Первый участник проводит деление сплошными вертикальными линиями, второй – пунктирными, третий – волнистыми.
Вот вариант деления всего объема работы на равные части, предложенный первым химиком (рис. 10.3).
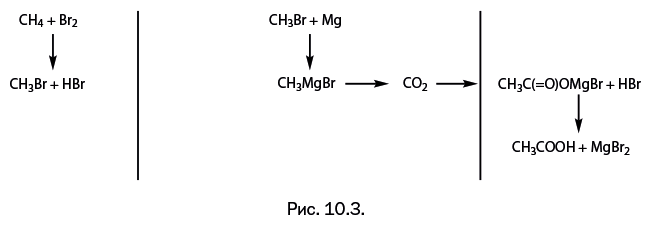
С точки зрения второго химика, деление работы на три равные части выглядит следующим образом (рис. 10.4).
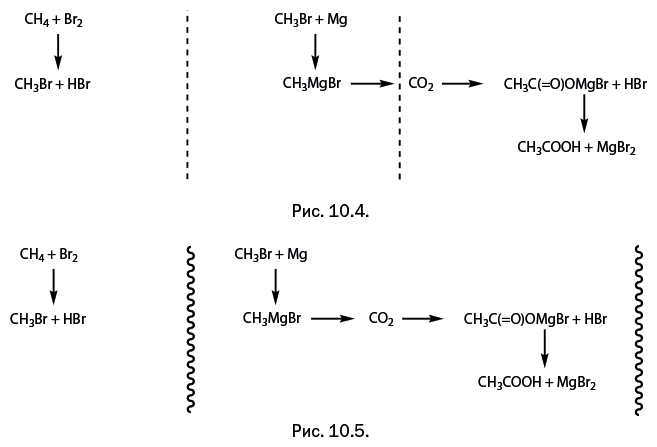
У третьего химика оказались свои оценки (рис. 10.5).
Решение задачи проведем графическим методом. Объединим все три варианта, наложив их друг на друга, а внизу с помощью фигурных скобок укажем объем работы, предлагаемый каждому участнику (рис. 10.6).
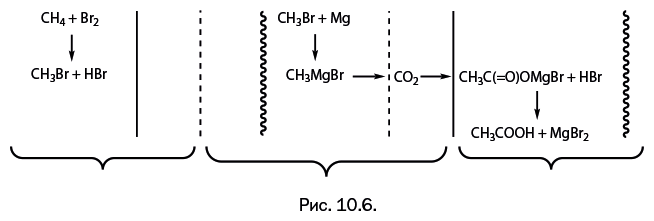
Обратите внимание на то, что объем работы первого участника, выбранный им самим, указан между двумя сплошными линиями, но ему предлагается заметно меньший объем. Все то же самое и у остальных двух участников. Фигурные скобки «предлагают» каждому из них меньший объем работы, чем тот, на который он рассчитывал. Таким образом, принцип справедливого разделения работы соблюден, причем такая задача имеет решение и при других оценках объема работы.
Итак, оценить в рублях или каким-либо иным способом – например, графически, как в последней задаче, – можно очень многое. Важно, что для подобных задач следует первоначально установить количественную меру для каждого объекта, и тогда решение будет найдено.
Мы немного увлеклись различными распределениями и оценками, забыв об элементарных истинах. Цену или количественную меру, конечно, можно назначить всему, но если химик увлечен каким-либо исследованием, то он, скорее всего, даже не задумывается о справедливом разделении работы и ее оплате. Вспомним, что не все продается и не все покупается. Просто и точно об этом сказал Булат Окуджава:
Чистое сердце в дорогу готовь!
Древняя мудрость годится и вновь.
Не покупается, не покупается
Доброе имя, талант и любовь!

