Книга: Лаборатория химических историй. От электрона до молекулярных машин
Назад: Необычные квартиры
Дальше: Это видели немногие
Каждому свои орбитали
Если форму р-орбиталей чаще всего обсуждают в учебниках органической химии, то следующие за ними пять d-орбиталей (пятикомнатная квартира) – любимая тема в координационной химии, рассматривающей свойства комплексных соединений. Эти орбитали появляются в четвертом периоде, и в каждом последующем периоде их всегда пять. Они начинают «заселяться» электронами у переходных элементов (чаще их называют d-элементами), начиная со скандия и кончая цинком. В таблице Менделеева они окрашены в цвет, отличающийся от s– и р-элементов. Формы d-орбиталей сложнее, чем у р-орбиталей: четыре из них имеют одинаковый внешний вид (четырехлопастной винт – а точнее, крестообразно расположенные четыре капли), но по-разному ориентированы в пространстве. Пятая d-орбиталь имеет необычную форму – это объемная восьмерка, продетая сквозь тор или, как говорят в быту, бублик. Обычно в книгах по координационной химии эти орбитали изображают так, как показано на рис. 4.11, независимо от того, к какому уровню они относятся.
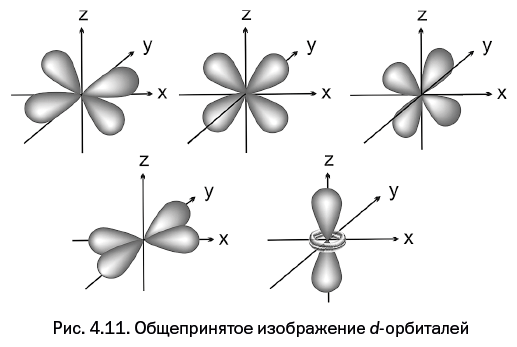
Интересно, что показанные на рис. 4.11 изображения почти не отличаются от истинных (рис. 4.12), но это относится только к орбиталям четвертого периода.

Следующий, пятый период воспроизводит предыдущий, в результате появляются новые d-элементы – от иттрия до кадмия, и в таблице они окрашены точно так же, как d-элементы предыдущего периода. Зная предысторию, мы могли предположить, что их внешний вид будет несколько иной, как и оказалось на самом деле (рис. 4.13).

Теперь уже не кажется удивительным, что d-орбитали следующего, шестого периода имеют еще более сложную форму (рис. 4.14). Каплеобразная форма сменяется грибообразной, и появляется нечто похожее на дополнительные ножки. На эти орбитали начинают «селиться» электроны в d-элементах шестого периода – от гафния до ртути.
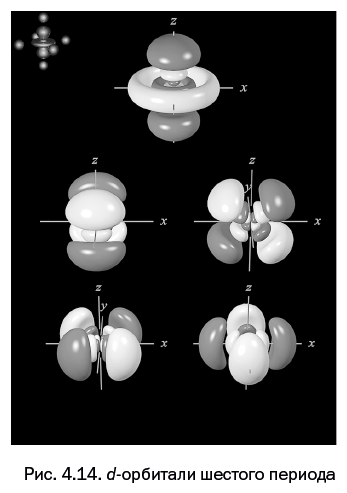
Если требуется только упрощенное изображение и качественное обсуждение формы, то можно условно принять, что все показанные d-орбитали имеют форму, аналогичную показанной на рис. 4.11. Но, к счастью, благодаря усилиям упомянутого ранее Марка Винтера мы можем увидеть, как все выглядит по результатам вычислений.
Назад: Необычные квартиры
Дальше: Это видели немногие

