Анализ затрат-выгод может стать хорошей отправной точкой для принятия решения. Но во многих случаях ваши варианты и связанные с ними затраты и выгоды не совсем ясны. Иногда в потенциальных результатах будет слишком много неопределенности. А еще бывают настолько сложные ситуации, что и с вариантами не все понятно. В таком случае придется использовать другие ментальные модели, чтобы выпутаться из такой сложности.

Рассмотрим относительно распространенную ситуацию, с которой сталкиваются владельцы жилья: дорогостоящий ремонт. Предположим, вы хотите отремонтировать оборудование для бассейна до начала купального сезона. Вы получаете предложения от двух подрядчиков. Одно предложение от компании, с которой вы постоянно работаете. Они, допустим, дают цену около 2 500 долларов – дороговато. Второе предложение обойдется дешевле – в 2 000 долларов, но этот подрядчик работает в одиночку, вы с ним еще не сотрудничали, и вдобавок вам кажется, что эта задача ему не совсем по силам.

Итак, у вас складывается впечатление, что существует всего 50 % вероятность того, что этот подрядчик своевременно закончит работу по указанной цене (за одну неделю). Если этого не произойдет, нужно оценить следующие сценарии:

• 25 % шанс, что он задержится на неделю и придется доплатить 250 долларов за дополнительный труд;

• 20 % шанс, что он задержится на две недели и придется доплатить 500 долларов;

• 5 % шанс, что ему не только понадобится на работу больше трех недель, но часть его работы придется переделывать и все дополнительные расходы составят 1 000 долларов.

Такая ситуация (несколько предложений с учетом сроков/качества) очень распространена, но из-за неопределенности ее довольно сложно анализировать с точки зрения одних только затрат и выгод. К счастью, есть простая ментальная модель, которую можно использовать, чтобы понять все эти потенциальные результаты: дерево решений. Это диаграмма, которая выглядит как дерево (лежащее на боку) и помогает анализировать решения с неопределенным результатом. Ветви (часто в виде квадратов) – это точки принятия решений, а листья представляют собой разные возможные результаты (часто в виде открытых кружков, обозначающих точки шансов). Дерево решений для ситуации с бассейном может выглядеть как на рисунке.

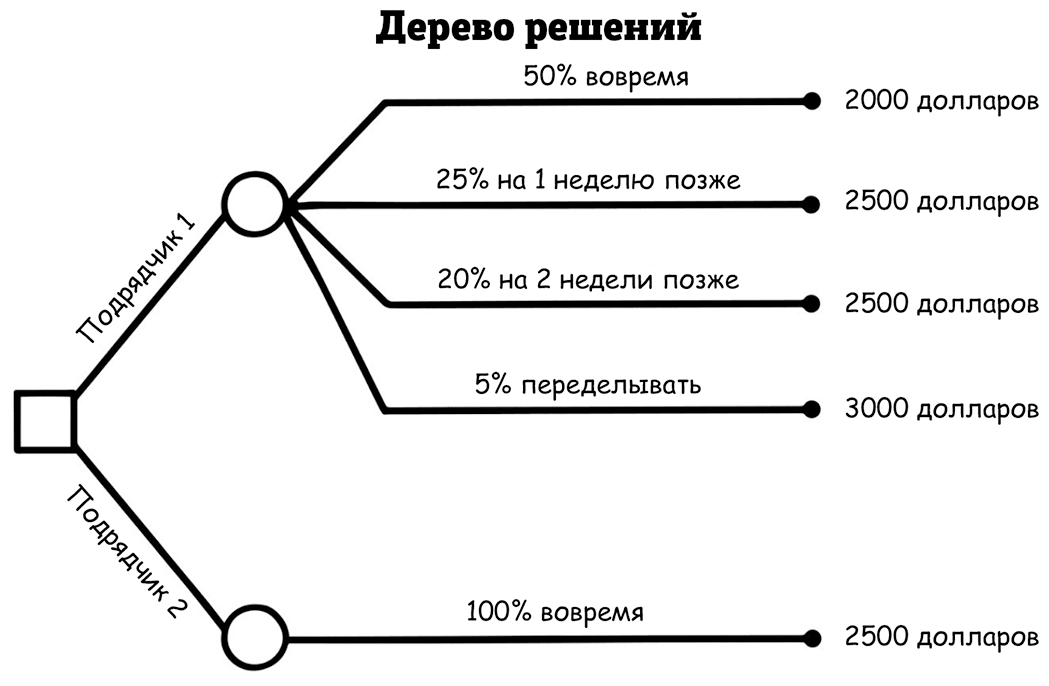
Первый квадрат представляет собой выбор между двумя подрядчиками, а открытые круги после него разветвляются на разные возможные результаты для каждого из этих вариантов. Листья с закрытыми кружками представляют собой итоговые затраты на каждый результат, а их вероятность указана в каждой строке (это простое распределение вероятностей), которое описывает, как все вероятности распределены относительно результатов. Каждая группа вероятностей суммируется до 100 %, отображая все возможные результаты для этого выбора.

Теперь вы можете использовать свои оценки вероятности, чтобы получить математическое ожидание для каждого подрядчика, перемножив вероятность каждого потенциального результата на его стоимость, а затем сложив все вместе. Полученное в сумме значение – это то, что вы ожидаете заплатить в среднем каждому подрядчику, учитывая все потенциальные результаты.

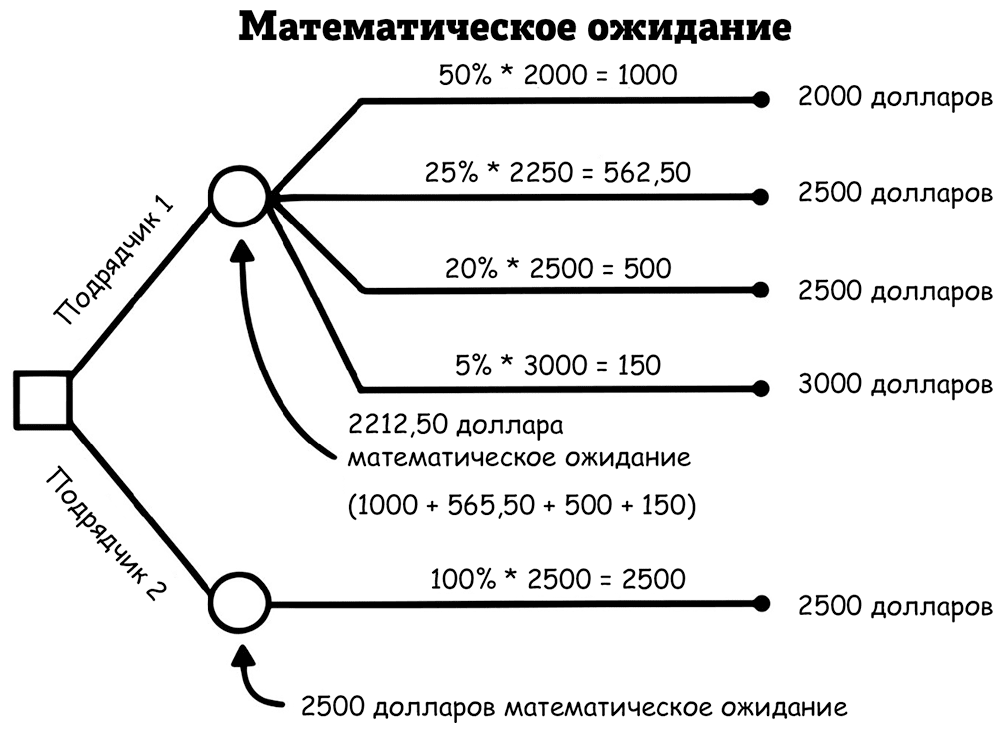
Математическое ожидание для вашего обычного подрядчика (подрядчик 2 на дереве решений) – всего 2500 долларов, поскольку возможен только один результат. Математическое ожидание для нового подрядчика (подрядчик 1 на дереве решений) – это сумма всех произведений по четырем возможным результатам: 1000 + 562,50 + 500 + 150 = 2212,50 доллара. Несмотря на то что один из результатов работы нового подрядчика будет стоить 3000 долларов, ожидаемая сумма, которую вы заплатите, все равно будет ниже, чем плата вашему обычному подрядчику.

Если эти вероятности точны и вы могли бы проиграть сценарий сто раз в реальном мире, где каждый раз выбирали бы нового подрядчика, ваша средняя выплата составила бы около 2212,50 доллара. Это потому, что в половине случаев вы будете платить всего 2000 долларов, а в другой половине – больше. Вы никогда не заплатите точно 2212,50 доллара, потому что это не является возможным результатом, но в целом все ваши платежи будут склоняться к этому математическому ожиданию в течение многих повторов.

Если вас это смущает, возможно, вас убедит следующий пример. В 2015 году у матерей в США в среднем было 2,4 ребенка. Было ли у какой-то определенной матери ровно 2,4 ребенка? Мы надеемся, что нет. У кого-то был один ребенок, у кого-то два, у кого-то три и т. д., и все это в среднем сводилось к 2,4. Точно так же различные результаты выплат подрядчикам и их вероятности складываются в математическое ожидание, несмотря на то что эту сумму в точности вы никогда не заплатите.

В любом случае, через призму дерева решений и математического ожидания можно рационально выбрать нового подрядчика, даже несмотря на все его потенциальные проблемы. Это потому, что ваши ожидаемые затраты будут ниже с этим подрядчиком.

Конечно, этот результат изменится с разными вероятностями и/или потенциальными выплатами. Например, если вы решите, что шанс заплатить 3 000 долларов составляет не 5 %, а 50 %, тогда математическое ожидание для нового подрядчика станет выше, чем ставка вашего обычного. Помните, что всегда можно провести анализ чувствительности для любых входных данных, которые, по-вашему, могут существенно повлиять на решение, как мы уже обсуждали в предыдущем разделе. Здесь вы будете варьировать вероятности и/или потенциальные итоговые выплаты и смотреть, как ожидание будет меняться соответственно.

Задумайтесь, что еще повлияет на это решение. Допустим, вы уже запланировали вечеринку у бассейна через несколько недель. Теперь, если подрядчик с более низкой ставкой протянет две недели, вы будете сильно переживать из-за вечеринки. Вам придется давить на него, чтобы он доделал работу, и, возможно, даже вызвать дорогостоящее подкрепление, чтобы помочь закончить ремонт. Очень много лишних хлопот.

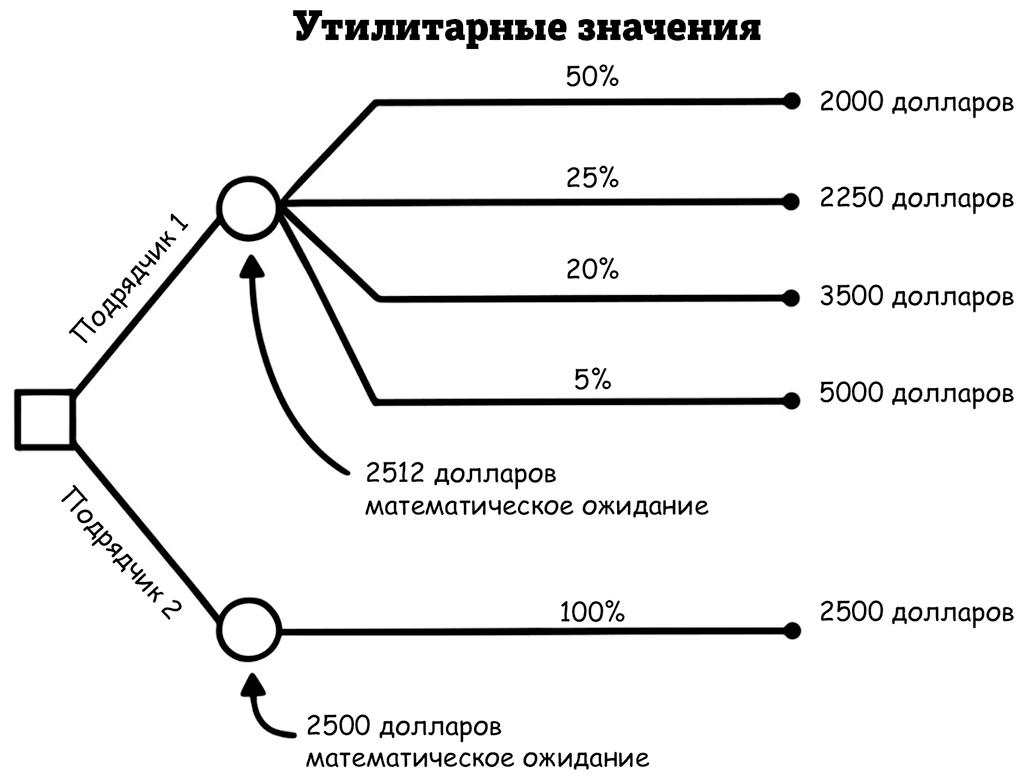
Человеку побогаче, чье время обладает более высокой альтернативной стоимостью, все это лишнее беспокойство и хлопоты можно оценить в лишнюю 1 000 долларов расходов, даже если эта 1000 не будет отдана напрямую подрядчику. Эта дополнительная нагрузка увеличит стоимость результата с опозданием на 2 недели с 2 500 долларов (раньше переплата составляла 500 долларов) до 3 500 долларов (теперь переплата составляет 1 500 долларов).

А если этот новый подрядчик действительно плохо сделает работу и вам придется звать старого, чтобы он срочно все переделывал, это будет вам стоить лишнюю 1 000 долларов за суету и нервы плюс реальные дополнительные расходы на оплату работы другого подрядчика. Итак, тот маленький шанс 5 %, что вам придется заплатить 3 000 долларов, в итоге может стоить вам лишних 2 000 долларов, то есть всего 5 000 долларов.

Показав эти возросшие значения на своем дереве решения, вы можете эффективно «учесть» дополнительные расходы. Из-за того что они включают в себя больше, чем стоимость одной только выплаты, они называются утилитарными значениями, которые отражают ваши общие относительные предпочтения в различных сценариях. Мы уже видели эту идею в предыдущем разделе, когда оценивали ваше предпочтение не иметь арендодателя.

Утилитарные значения можно отвязать от настоящих цен, поскольку вы можете ценить что-то одно больше, чем другое, даже если на открытом рынке эти варианты стоят одинаково. На это влияют ваши предпочтения. Подумайте о своей любимой группе – их концерт даст вам больше, чем концерт другой по той же цене. Просто потому, что они вам больше нравятся. Стресс из-за починки бассейна – это дополнительная потеря утилитарности, которая прибавится к настоящим расходам на работу подрядчиков.

Результаты на листьях дерева решений могут стать утилитарными значениями, объединяющими все затраты и выгоды (материальные и нематериальные) в одном числе для каждого варианта. Если вы сделаете это, ваше решение изменится в противоположную сторону – лучше будет обратиться к вашему обычному подрядчику (подрядчик 2 на дереве решений).

Обратите внимание, что эти решения все еще очень близки, так как у обоих подрядчиков теперь практически одно и то же математическое ожидание! Эта близость показывает силу вероятностных результатов. Несмотря на то, что новый подрядчик связан с более высокими потенциальными «затратами», в 50 % случаев вы все равно рассчитываете заплатить ему гораздо меньше. Эта меньшая сумма сильно снижает математическое ожидание из-за частоты такого результата.

Если ситуация позволяет, мы настоятельно рекомендуем использовать утилитарные значения, поскольку они показывают более полную картину ваших основных предпочтений и приводят к более удовлетворительным решениям. На самом деле, в более широком смысле существует философия под названием утилитаризм, которая утверждает, что самым этичным решением является то, которое приносит больше всего пользы – утилитарности – всем участникам.

У философии утилитаризма есть множество недостатков. В первую очередь полезные решения, касающиеся многих людей, могут казаться довольно несправедливыми, когда эта полезность неравномерно распределена среди участников (например, неравные доходы, несмотря на растущий уровень жизни). Также утилитарные значения бывает сложно оценить.

В любом случае, деревья решений помогут понять, что делать в ситуациях с большим количеством разнообразных вероятностных исходов. Подумайте о медицинском страховании – стоит ли вам взять план с высокой франшизой и низкими выплатами или с низкой франшизой и высокими выплатами? Это зависит от уровня обслуживания, которого вы ожидаете, и от того, можете ли вы позволить себе менее вероятный сценарий, где вам понадобится выплатить высокую франшизу. (Обратите внимание, что ответ неочевиден, так как по плану с менее высокой франшизой вы будете делать более высокие ежемесячные взносы. Это увеличение взносов может рассматриваться как выплата части вашей франшизы каждый месяц.) Изучите этот сценарий и подобные ему через дерево решений, учитывая ваши предпочтения наряду с фактическими затратами.

Деревья решений особенно полезны, чтобы думать о маловероятных, но очень значительных событиях. Рассмотрите подробнее сценарий медицинского происшествия, при котором вам потребуется выплатить полную франшизу. Некоторых людей такие затраты приводят к банкротству, и поэтому истинная стоимость такого события намного выше, чем фактическая стоимость франшизы.

В результате, если вы окажетесь в этой ситуации, вам стоит показать потери утилитарного значения для этого сценария очень высокими, чтобы отразить свое желание избежать банкротства. Вероятно, это подтолкнет вас к плану с высокой выплатой и низкой франшизой (насколько вы сможете себе их позволить) и с большей гарантией того, что вы избежите банкротства. Другими словами, если возможен финансовый крах, стоит избегать такого плана, даже если в среднем у него лучший финансовый результат.

В этом типе анализа следует остерегаться «черного лебедя» – экстремального события с серьезными последствиями (вроде финансового краха), которые намного более вероятны, чем вы изначально ожидаете. Такое название термин получил благодаря распространенному в Европе ложному убеждению, что черных лебедей не существует, хотя на самом деле они всегда заселяли территорию Австралии.

Говоря о «черном лебеде» в контексте анализа через дерево решений, вы должны увеличить оценки вероятности маловероятных, но очень значительных сценариев, например банкротства.

Одна из причин, по которой вероятность «черных лебедей» оценивается ошибочно, связана с нормальным распределением, которое представляет собой распределение вероятности в форме колокола и объясняет частоту многих природных явлений (например, человеческого роста). При нормальном распределении редкие события находятся на хвостах распределения (например, очень высокие или невысокие люди), далеко от центра колокола. Но «черные лебеди» часто исходят из распределения с «толстыми хвостами», которые буквально имеют толстые хвосты: то есть события, удаленные от центра, намного вероятнее, чем при нормальном распределении.

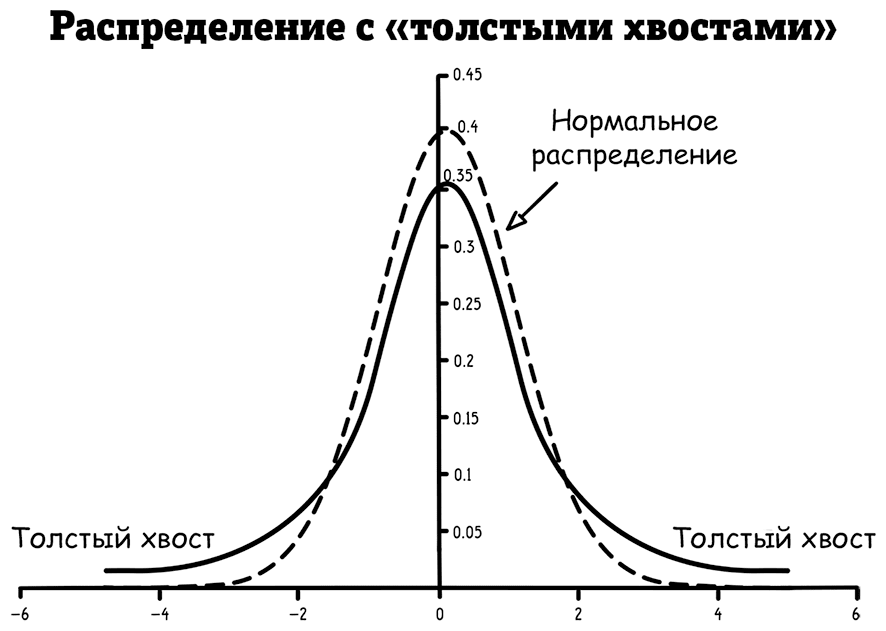
В природе встречается немало распределений с толстым хвостом, и иногда люди просто ошибочно считают, что имеют дело с нормальным распределением. На самом деле перед ними распределение с толстым хвостом, и события в хвосте происходят с более высокой вероятностью. На практике это те распределения, где самые тяжелые последствия возникают чаще, чем при нормальном распределении: так происходит со страховыми выплатами или с распределением доходов в США.

Другая причина, по которой вы ошибочно рассчитываете вероятность «черного лебедя», – это недопонимание их причин. Вы думаете, что у ситуации есть только одно распределение, но на самом деле их несколько. Существуют генетические мутации (например, карликовость и синдром Марфана), из-за которых низких или высоких людей может быть больше, чем при обычном нормальном распределении, где не учитываются эти более редкие генетические вариации.

Третья причина заключается в том, что вы недооцениваете вероятность и влияние каскадных сбоев. В сценарии с каскадным сбоем части системы взаимосвязаны: если в одной происходит сбой, в следующей тоже происходит сбой и т. д. Примером этой ситуации является финансовый кризис 2007–2008 годов: банкротство ценных бумаг, обеспеченных ипотекой, каскадом затронуло банки и связанные с ними страховые компании.

Еще один пример – климат. Термином потоп столетия обозначается потоп, который с вероятностью 1 % может произойти в любой из отдельно взятых годов. К сожалению, изменение климата повышает вероятность такого бедствия. Хотя раньше оно происходило с вероятностью 1 раз в 100 лет, во многих регионах она теперь превышает 1 %. Ничего уже не поделаешь. В Хьюстоне, штат Техас, было три так называемых наводнения пятисотлетия за последние три года! Вероятности этих событий явно нужно корректировать по мере того, как каскадные последствия климатических изменений будут усиливаться.

Для сложных систем типа банков или изменений климата недостаточно просто провести анализ методом дерева решений или затрат-выгод – нужно осмыслить всю систему. Системное мышление – это мышление обо всей системе одновременно. Так вы с большей вероятностью поймете и учтете тонкие взаимодействия между компонентами, которые в противном случае приведут к непредвиденным последствиям. Например, думая об инвестиции, нужно понимать, как, казалось бы, несвязанные части экономики влияют на результат.

Какие-то системы легко представить, другие настолько сложны, что буквально рассыпаются на кусочки, стоит о них подумать. Выход прост – нарисуйте систему в виде диаграммы. Рисование диаграмм помогает лучше понять сложные системы и взаимодействие их компонентов.

Методы эффективного представления сложных систем в виде диаграмм не укладываются в рамки этой книги, но знайте, что можно освоить множество техник, включая диаграммы каузальных петель (которые показывают петли обратной связи в системе) и диаграммы запасов и потоков (которые показывают, как вещи накапливаются и потоком направляются в систему). Магистерская работа Габриэля состояла в построении диаграммы для спам-фильтров в электронной почте. Ниже представлена одна из его диаграмм каузальных петель – вам не нужно ее понимать, это пример. Просто знайте, что это один из эффективных способов осмысления сложных систем.

В качестве следующего шага можно использовать программное обеспечение для имитации системы, которое называются симуляцией. Существуют программы, которые позволяют составить диаграмму системы на экране, а затем немедленно превратить ее в рабочую симуляцию (в режиме онлайн это делают две программы: Insight Maker и True-World). В процессе вы можете задать начальные условия, а затем посмотреть, как система будет разворачиваться с течением времени.

Симуляции позволяют глубже понять сложную систему и точнее предсказать «черных лебедей» и другие события. Они также помогают определить, как система будет приспосабливаться к изменяющимся условиям. Принцип Шателье, названный в честь французского химика Анри-Луи Ле Шателье, гласит, что, когда любая химическая система, находящаяся в равновесии, подвергается изменению условий, например температуры, объема или давления, она подстраивается под новое равновесное состояние и, как правило, частично нейтрализует перемену.

Например, если кто-то вручит вам тяжелую коробку, вы не упадете. Вы перераспределите свой вес с учетом добавленного. Или в экономике, когда вводится новый налог, налоговые поступления от него в конечном счете будут ниже, чем можно было бы ожидать в нынешних обстоятельствах, поскольку люди меняют свое поведение во избежание уплаты этого налога.

Эта идея звучит знакомо, потому что принцип Шателье похож на ментальную модель гомеостаза из биологии: вспомните, как ваше тело автоматически начинает дрожать или потеть в ответ на внешние условия, чтобы регулировать внутреннюю температуру. Принцип Шателье не значит, что система будет подстраиваться под определенные значения, но она будет реагировать на внешние условия, и обычно так, чтобы частично нейтрализовать внешний стимул. Вы можете увидеть этот принцип в действии в реальном времени с помощью симуляций, потому что они позволяют подсчитать, как симулированная система будет приспосабливаться к различным переменам.

Связанная ментальная модель, которая также возникает в динамических системах и симуляциях, – это гистерезис, описывающий, как текущее состояние системы зависит от ее истории. Гистерезис также встречается в природе и имеет примеры в большинстве научных дисциплин. В физике, когда вы намагничиваете материал, например, удерживая магнит на куске металла, этот металл не полностью теряет магнитный заряд после того, как вы уберете магнит. В биологии Т-клетки, питающие вашу иммунную систему, после активации требуют более низкого порога для реактивации. Благодаря гистерезису металл и Т-клетки отчасти запоминают свое состояние, и то, что произошло раньше, влияет на то, что произойдет дальше.

Опять же эта идея кажется знакомой, потому что она похожа на ментальную модель зависимости от пути, которая более подробно описывает, как ваш выбор впоследствии ограничивает число ваших вариантов в будущем. Гистерезис – это один из типов зависимости от пути применительно к системам.

Например, в инженерных системах полезно встроить в систему определенный гистерезис, чтобы избежать стремительных изменений. Современные термостаты делают это, допуская диапазон температур, близкий к заданному значению: если вы хотите поддерживать температуру 70 ℉ (21,1 ℃), термостат можно настроить так, чтобы обогреватель включался, когда температура падает до 68 ℉ (20 ℃), и выключался, когда она вырастает до 72 ℉ (22,2 ℃). Таким образом, он не будет постоянно включаться и выключаться. Точно так же на сайтах дизайнеры и разработчики устанавливают задержку при перемещении курсора мыши на такие элементы страницы, как меню. Программы запоминают, что вы просматривали меню, и, когда вы уводите с него курсор, оно не пропадает резко.

Используйте все эти ментальные модели для визуализации и симуляции сложных систем, чтобы лучше оценивать потенциальные результаты и связанные с ними вероятности. Применяйте эти результаты в более простой модели для принятия решения, например для дерева решений или анализа затрат-выгод.

Отдельный тип симуляции, который особенно полезен в этом случае, – это симуляция по методу Монте-Карло. Как и критическая масса, эта модель возникла в ходе Манхэттенского проекта в Лос-Аламосе в преддверии открытия атомной бомбы. Физик Станислав Улам затруднялся с использованием традиционной математики в определении того, как далеко нейтроны могут проходить сквозь различные материалы, и придумал новый метод, разложив пасьянс (ну да, карточный). Вот как он сам описывает это в журнале «Науке Лос-Аламоса»:

Симуляция по методу Монте-Карло – это, на самом деле, множество независимых симуляций со случайными начальными условиями или использованием других случайных чисел внутри самой симуляции. Проведя симуляцию системы много раз, вы начнете понимать, насколько вероятны на самом деле различные результаты. Считайте это динамическим анализом чувствительности.

Симуляции по методу Монте-Карло используются почти во всех областях науки. Но они полезны и за ее пределами. Например, венчурные капиталисты часто используют эти симуляции чтобы определить, какой капитал зарезервировать для будущего финансирования. Когда венчурный фонд инвестирует в компанию, эта компания в случае успеха, вероятно, заработает больше денег в будущем, и фонд захочет отчасти финансировать ее, чтобы сохранить свой процент владения. Сколько денег ему зарезервировать для этой компании? Не все компании достигают успеха и собирают разные суммы, так что ответ не так однозначен во время первоначальной инвестиции. Многие фонды используют симуляции по методу Монте-Карло, чтобы понять, сколько им нужно резервировать, учитывая их текущую историю, подсчеты успешности компании и размер потенциального финансирования.

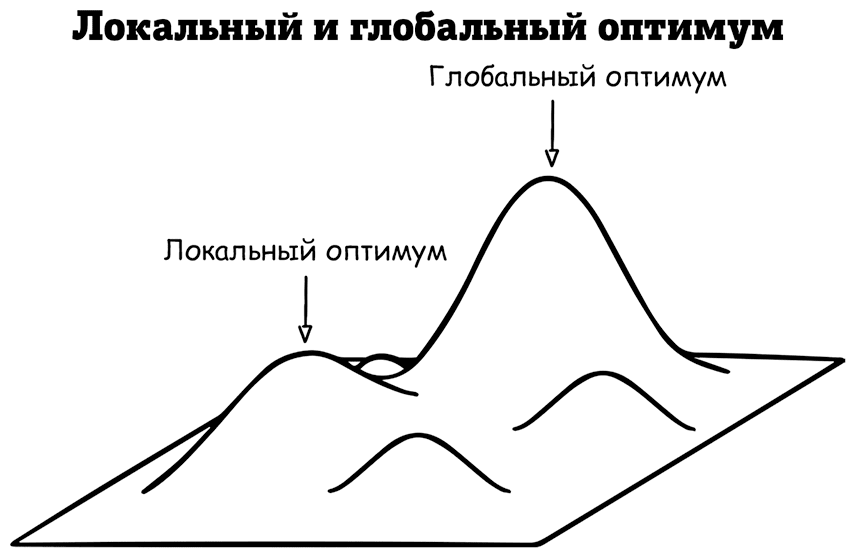
В более общем плане попытка понять сложные системы с помощью системного мышления – диаграмм, симуляций или других ментальных моделей – помогает не только получить общее представление о системе и о диапазоне результатов в ней, но также узнать наилучшие возможные результаты. Без такого знания вы застрянете в погоне за локальным оптимумом – решением, которое, возможно, и хорошее, но не лучшее.

Если есть возможность, вам следует стремиться к наилучшему решению, которое будет глобальным оптимумом. Подумайте о катании с горки: вам подойдет и ближайшая горка (локальный оптимум), но вдалеке есть высокий холм, который намного удачнее (глобальный оптимум). Вам нужно дойти до того высокого холма. Но для начала нужно получить полное представление о системе, чтобы понять, что высокий холм существует.