Раз уж мы заговорили о вращающихся телах, о том, что их притяжение значительно сложнее, чем у точечных масс, поговорим же и о том, во что превращаются вращающиеся тела, если их раскручивать всё быстрее и быстрее. На рис. 4 показана довольно любопытная последовательность фигур равновесия самогравитирующих тел. Странным словом «самогравитирующее» обозначают тот факт, что тело подвержено только действию собственной силы тяжести, которой противостоит внутреннее изотропное давление. Рисунок построен в координатах “квадрат безразмерного углового момента j — квадрат безразмерной угловой скорости w”:

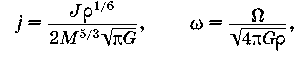
где М, р, J и Ω — масса, плотность, момент импульса и угловая скорость вращения тела. Линии на рисунке показывают решения уравнений равновесия, т. е. указывают, с какой угловой скоростью будет стационарно вращаться тело, обладающее определённым моментом импульса. Сплошными линиями указаны решения для жидких тел. Почему жидких? Это удобная абстракция: идеальная жидкость под давлением не меняет свою плотность, но при изменении вращения меняет форму: поверхность жидкости всегда перпендикулярна сумме всех действующих на неё сил (включая центробежные). При этом уравнения равновесия решаются сравнительно легко (р = const), а некоторые космические тела, например, планеты, действительно можно считать жидкими, поскольку их плотность слабо меняется с глубиной. Но для нормальных звёзд эта абстракция уже не подходит: плотность их вещества очень сильно меняется от центра к поверхности. Поэтому для них рассчитана последовательность фигур сжимаемых тел (фигуры Джинса).

Сначала представим себе совсем не вращающееся жидкое тело, обладающее гравитацией. Разумеется, оно шарообразно. Начнём раскручивать тело, сообщая ему всё больший угловой момент. При этом угловая скорость тела начинает расти, а его фигура становится всё более и более сплюснутым эллипсоидом вращения, который по традиции называют сфероидом Маклорена. Эволюционируя вдоль последовательности Маклорена, тело достигает точки максимума угловой скорости. При дальнейшем увеличении углового момента наш эллипсоид настолько уплощается, что начинает быстро возрастать его момент инерции (за счёт удаления массы от оси вращения), а угловая скорость вращения при этом уменьшается. Тело становится всё более плоским и похожим на диск.

Вам может показаться, что в приложении к космическим телам наше исследование лишено смысла: где это видано, чтобы кто-то раскручивал планету или звезду. Замечу, что иногда бывают ситуации, когда взаимодействие двух близких тел (например, планеты и её спутника) приводит к существенному изменению их момента импульса. Но чаще тела действительно сохраняют свой момент, однако заметно изменяют свою плотность. Например, в ходе формирования звезды из разреженного облака её размер уменьшается почти в миллион раз, а плотность возрастает в ~ 1017 раз! Математически это эквивалентно росту j. Докажите сами, что и движение вдоль последовательности Маклорена при этом происходит от шара к диску. Продолжим наш мысленный эксперимент.

На рисунке мы видим, что от последовательности фигур Маклорена в двух точках, называемых точками бифуркации, отходят новые кривые. Это также последовательности фигур равновесия, которые были открыты позже, чем сфероид Маклорена. Если мы сообщим телу момент импульса чуть больший, чем у первой точки бифуркации, и немножко возмутим его форму, оно может скачком превратиться из «тыквообразного» сфероида Маклорена в «дынеобразный» эллипсоид Якоби, т. е. станет не сплюснутым, а вытянутым и будет устойчиво вращаться вокруг оси, перпендикулярной направлению этой вытянутости. Если раскручивать тело сильнее, то оно будет становиться всё более вытянутым, пока не превратится в длинную спицу.

Вторая точка бифуркации на кривой Маклорена связана с превращением диска в кольцо. При определённом моменте выше критического диск становится неустойчивым: за счёт центробежных сил вещество из его серединки может в какой-то момент отскочить к периферии, и получится кольцо. Казалось бы, это математическая экзотика, но совсем недавно в космосе, среди формирующихся звёзд были обнаружены именно такие объекты.

На линии Якоби мы также видим точку бифуркации. У сильно вытянутого эллипсоида при моменте импульса больше некоторого критического вещество может из центра отойти к краям, создав в центре «перемычку», аналогичную дырке в кольце. Получается гантелеобразная фигура — гантель Пуанкаре.

Почти каждая из представленных здесь фигур носит имя известного математика или физика. Видите, как просто можно прославить своё имя в науке: достаточно найти новую фигуру равновесия вращающегося тела. Советую попробовать. Впрочем, пробовали уже многие: на рисунке представлены далеко не все возможные формы вращающихся жидких тел; но вы уже видите, насколько сложны могут быть эти формы. А ведь любая из них может быть присуща как планете, так и звезде; а это значит, что их соседи-спутники будут взаимодействовать не с материальной точкой, а например, вот с такой бешено вращающейся гантелью. Представляете, какая интересная задача для математика — исследовать движение спутника такой гантели?