Глава 3. Спад нейронных сетей

Единственным доказательством того, что даже самые сложные проблемы ИИ могут быть решены, является тот факт, что природа уже справилась с этими трудностями. В 1950-х годах появились подсказки, ключи для разгадки, которые предполагали принципиально новый подход к обработке символов, что могло обеспечить интеллектуальное поведение компьютера.

Первая подсказка: мозг – мощный распознаватель образов. Ваша зрительная система может распознать объект на изображении всего за десятую долю секунды, даже если вы никогда ранее его не видели. Кроме того, объект может быть любой формы, находиться на произвольном расстоянии и в любом положении по отношению к вам. Это все равно, что иметь особый компьютер, единственная функция которого – распознавание предметов.

Вторая подсказка – с помощью практики можно научить мозг выполнять задания любой сложности, будь то игра в теннис или задачи по физике. Природа использует обучение общего назначения для решения различных проблем, а человек, в свою очередь, прекрасный ученик. Это наша суперспособность. Структура коры головного мозга у всех схожа, а глубокие нейронные сети есть во всех сенсорных и моторных системах.

Третья подсказка – наш мозг изначально не наполнен правилами или логикой, но мы можем начать мыслить логически и следовать правилам после длительного обучения, хотя тут преуспеет далеко не каждый. Это наглядно проиллюстрировано логической головоломкой – задачей выбора Уэйсона (рис. 3.1).

Правильный ответ: карту с номером 8 и карту с коричневой рубашкой. Исследования показали, что только 10 процентов людей отвечают правильно. Тем не менее у большинства опрашиваемых нет проблем с правильным ответом, если ситуация в вопросе знакомая (рис. 3.2).

Рис. 3.1. На каждой из четырех карт с одной стороны цифра, с другой – цветная рубашка. Какую(ие) карту(ы) вы должны перевернуть, чтобы проверить истинность утверждения, что если на карте четное число, то ее противоположная сторона красная?

Рис. 3.2. На каждой карте указан возраст с одной стороны и изображен напиток с другой. Какую(ие) карту(ы) нужно перевернуть, чтобы проверить закон, по которому вы должны быть старше 18 лет, чтобы пить алкоголь?

Рассуждения кажутся зависимыми от области, о которой идет речь, и чем ближе вам область, тем легче вам решать проблемы в ней. Опыт упрощает рассуждения, потому что вы можете использовать примеры, с которыми столкнулись при интуитивном решении. В физике, например, вы изучаете определенную область (скажем, электричество и магнетизм), и именно это помогает вам при решении многих задач, а не запоминание формул. Если бы человеческий интеллект основывался только на логике, то область знаний должна была бы быть единой, а это не так.

Четвертая подсказка – мозг состоит из миллиардов крошечных нейронов, контактирующих друг с другом. Это говорит о том, что мы должны изучать класс массово-параллельных архитектур для решения проблем ИИ, а не архитектуру цифровых компьютеров фон Неймана, в которой процессор отделен от памяти узким каналом, через который данные и инструкции извлекаются и выполняются по одному. Действительно, машина Тьюринга может посчитать любую вычислимую функцию, имея достаточно памяти и времени, но она медленная и ее трудно программировать, а природа должна была решать проблемы в режиме реального времени. У самых мощных компьютеров на планете – массово-параллельные процессоры. Алгоритм, эффективно работающий на них, в конечном счете победит.

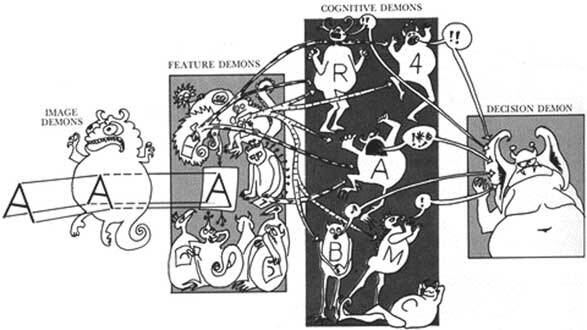
Рис. 3.3. Пандемониум. Оливер Селфридж представил, что в мозге есть демоны, которые ответственны за последовательное извлечение более сложных признаков и абстракций из сенсорных органов восприятия, что и приводит к принятию решений. Каждый демон на каждом уровне оживляется, если он соответствует входу с более раннего уровня. Решение демона взвешивает степень оживления и важность его информаторов. Эта форма оценки информации – метафора для современных сетей глубокого обучения, у которых гораздо больше уровней

Первооткрыватели

В 1950–1960-х годах произошел взрыв интереса к самоорганизующимся системам. Норберт Винер создал кибернетику на основе систем связи и управления как машин, так и живых существ. Оливер Селфридж разработал «Пандемониум» – систему распознавания образов, в котором выполняющие функцию обнаружения «демоны» выступали за право представлять объекты на изображениях, что является метафорой для глубокого обучения (рис. 3.3). Бернард Уидроу из Стэнфорда и его студент Тед Хофф создали алгоритм обучения LMS (Least Mean Squares; алгоритм минимальной среднеквадратичной ошибки), который широко используется для адаптивной обработки сигналов при регулировке шумов вдоль линий передачи, например телефонного кабеля. У алгоритма LMS и его последующих версий множество функций, начиная от шумоподавления и заканчивая финансовыми прогнозами. Это лишь несколько примеров, иллюстрирующих расцвет гениальных идей в 1960-х годах. Здесь я заострю свое внимание всего на одном первопроходце, Фрэнке Розенблатте (рис. 3.4), разработавшем перцептрон – прямой предшественник глубокого обучения.

Обучение на примерах

Первопроходцев нейронных сетей не отпугнуло, что мы не понимали функции мозга, и они сосредоточились на схематичных версиях нейронов и том, как они связаны друг с другом. Фрэнк Розенблатт из Корнелльского университета в США (рис. 3.4) был одним из первых, кто сымитировал строение нашей зрительной системы для автоматического распознавания образов. Он изобрел обманчиво простую систему под названием перцептрон, которая могла научиться классифицировать образцы по категориям, например по буквам алфавита. Розенблатт был застенчивым холостяком, но любил погонять на спортивной машине вокруг университетского кампуса. Он был эрудитом с широким кругом интересов, в том числе его интересовал поиск планет у далеких звезд через измерение постепенного падения яркости звезды, когда планета проходит мимо нее. Этот метод в настоящее время часто используется для обнаружения планет, типичных для нашей галактики.

Если вы понимаете основные принципы того, как перцептрон учится решать проблему распознавания образов, вы на полпути к пониманию работы глубокого обучения. Цель перцептрона – определить, является ли входной образ элементом категории на изображении. В Блоке 1 объясняется, как входные данные перцептрона преобразуются набором веса из входных единиц в выходные. Вес – это мера влияния каждого входа на окончательное решение, принятое блоком вывода. Как мы можем определить оптимальный набор весов для правильной классификации получаемой информации?

Рис. 3.4. Фрэнк Розенблатт в Корнелльском университете, погруженный в свои мысли. Он изобрел перцептрон – ранний предшественник сетей глубокого обучения, в основе которого лежал простой обучающий алгоритм для классификации изображений по категориям, например определяя, левая это сторона или правая. Заметка была опубликована в New York Times 8 июля 1958 года по сообщению агентства United Press International. Сто тысяч долларов в 1958 году в наши дни равноценны одному миллиону долларов. 704 компьютера IBM, стоившие два миллиона долларов, сегодня стоили бы двадцать миллионов долларов. 704 компьютера IBM могли выполнить двенадцать тысяч умножений в секунду, что считалось молниеносным по меркам того времени. Но смартфон Samsung S6 может совершить 34 миллиарда умножений в секунду, а это более чем в миллион раз быстрее и гораздо дешевле

Традиционный способ, который используют инженеры для решения этой задачи, – создание веса вручную на основе анализа или ситуативно для конкретной цели. Он трудоемок и часто базируется не только на инженерных разработках, но и на интуиции. В качестве альтернативы применяется автоматическая процедура, которая учится на примерах так же, как мы познаем окружающий мир. Необходимо множество примеров, включая те, что относятся к другим областям, особенно сходным: чтобы научиться распознавать кошек, нужно увидеть и собак. Примеры по одному вносятся в перцептрон, и при ошибке вес автоматически корректируется. Это называется обучающим алгоритмом. Алгоритм – пошаговая инструкция, которой вы следуете для достижения цели, например рецепт приготовления пирога. В главе 13 мы рассмотрим алгоритмы в целом.

Прелесть обучающей системы перцептрона в том, что он гарантированно сам найдет набор весов, если таковой существует и есть достаточно примеров. Обучение проходит постепенно, после того как представлен каждый из предметов в обучающем наборе, и результат сравнивается с правильным ответом. Если ответ верный, в вес не вносится никаких изменений. Но если ответ неправильный (1, когда должно быть 0, или 0, когда должно быть 1), то вес постепенно меняется, и в следующий раз, когда поступит такой же запрос, он будет ближе к правильному ответу (блок 1). Важно, чтобы изменения происходили постепенно, для того чтобы вес зависел от всех тренировочных примеров, а не только от последнего.

Блок 1. Перцептрон

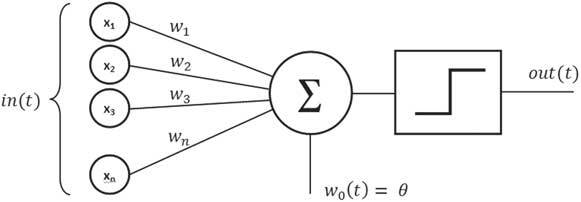
Перцептрон – это нейронная сеть с одним нейроном, которая имеет входной слой и набор соединений, связывающих входные блоки с выходным блоком. Цель перцептрона – классифицировать образцы, поступающие в блок входа. Основная функция, выполняемая блоком вывода, – суммирование значений каждого входного сигнала, помноженного на вес его связи с блоком вывода. На диаграмме вес (w_n) суммы входных сигналов (х_n) сравнивается с порогом θ и проходит через ступенчатую функцию, которая дает на выходе единицу, если сумма больше порогового значения, и ноль – если меньше. Например, входными данными могут быть пиксели изображения или, в более широком смысле, основная информация, извлеченная из необработанного изображения, такая как контур объекта. Изображения представляются по одному, и перцептрон решает, входило ли оно в категорию, например, кошек. Блок вывода может быть только в одном из двух состояний: «включен», если изображение относится к данной категории, и «выключен», если не относится. «Включен» и «выключен» соответствуют 1 и 0 в двоичной системе. Обучающий алгоритм перцептрона выглядит следующим образом:

δ w_i = α δ x_i

δ = вывод – учитель,

где вывод и учитель являются двоичными, так что δ равно нулю, если вывод правильный. Если выход неправильный, δ равно +1 или –1 в зависимости от разницы.

Если объяснение работы перцептрона не ясно, есть более четкий геометрический способ, помогающий понять, как перцептрон учится распознавать входящую информацию. Для частного случая двух типов входных данных можно нанести входные данные на двумерный график. Каждый вход представляет собой точку на графике, а два веса в сети определяют прямую линию. Цель обучения – провести линию таким образом, чтобы она четко разделяла положительные и отрицательные примеры (рис. 3.5). Для трех типов входных данных пространство входа трехмерное, и перцептрон задает плоскость, разделяющую положительные и отрицательные обучающие примеры. В общем случае размерность пространства входов может быть довольно высокой и ее будет невозможно визуализировать, но принцип остается тем же.

В конце концов, если появится решение, вес перестанет меняться, и значит, все примеры в обучающем наборе классифицированы правильно. Здесь нужно соблюдать осторожность, потому как в обучающем наборе, возможно, было недостаточно примеров, и сеть просто запомнила конкретные образцы, не имея шанса обобщить их в новой для нее ситуации. Это называется чрезмерным обучением, или переобучением. Важно иметь другой, контрольный набор примеров, который не был использован для обучения сети. В конце обучения результат классификации тестового набора является истинным показателем того, насколько хорошо перцептрон может обобщить новый пример, категория которого неизвестна. Обобщение здесь ключевое понятие. В реальной жизни мы никогда не видим тот же объект одинаково и не сталкиваемся с той же ситуацией, но если мы сможем обобщить предыдущий опыт и спроецировать его на новую ситуацию, нам удастся справиться с широким спектром реальных проблем.

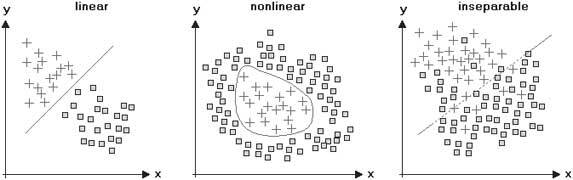
Рис. 3.5. Геометрическое объяснение того, как перцептрон распознает две категории объектов. У объектов есть две характеристики – длина и яркость, – их значения (x, y) отображены на графике. На графике слева оба типа объектов (плюсы и квадраты) возможно разделить прямой линией, которая пройдет между ними. Это различие может быть изучено перцептроном. В двух других областях объекты нельзя разделить прямой линией, но на центральном графике их можно разделить кривой. С выборкой справа надо провести некие махинации, чтобы разделить объекты двух типов. Все три класса могут быть изучены глубокой сетью, если есть достаточно данных для обучения