Машины Больцмана

В сети Хопфилда имитация отжига соответствует «нагреву» обновлений, так что энергия может идти как вверх, так и вниз. При высокой температуре блоки произвольно переворачиваются, и если температура постепенно понижается, то высока вероятность того, что сеть Хопфилда застынет в состоянии с наименьшей энергией, когда температура достигнет нуля. На практике моделирование начинается при постоянной температуре, чтобы обеспечить равновесие сети. При равновесии сеть может побывать во множестве ближайших состояний и исследовать широкий спектр допустимых решений.

Блок 4. Машина Больцмана

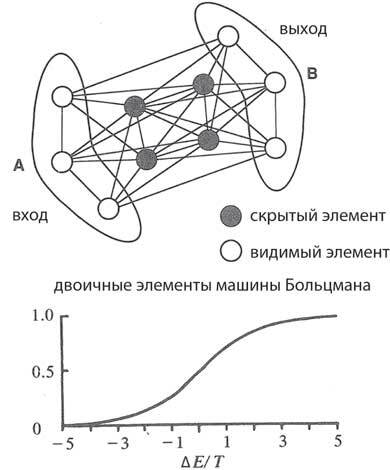
Все соединения в машине Больцмана симметричны, как и в сети Хопфилда, и двоичные единицы обновляются один раз, устанавливая s_i = 1 с вероятностью, заданной приведенной выше S-образной кривой, где входы ∆ E масштабируются по температуре T. Входной и выходной слои «видимы» в том смысле, что они взаимодействуют с внешним миром. «Скрытые элементы» представляют объекты, имеющие внутренние степени свободы, которые могут влиять на видимые объекты. У алгоритма машинного обучения Больцмана две фазы: в фазе бодрствования входы и выходы фиксируются, и после того, как сеть приходит к равновесию, вычисляется средняя корреляция между парами единиц. Во второй фазе сна корреляции снова вычисляются с незафиксированными входами и выходами. Затем вес постепенно обновляется:

Δw_ij=ε(<s_is_j>^{бодрствование} – <s_is_j>^сон).

Для примера рассмотрим задачу, где требуется определить, какая часть изображения является фигурой, а какая – фоном. Фигура на рис. 7.3 неоднозначна, и в зависимости от того, на какую часть вы обратите внимание, вы увидите вазу или два лица, но не то и другое сразу. Мы разработали машину Больцмана (блок 4), которая моделирует выбор между фигурой и фоном. Она состояла из элементов, часть из которых в состоянии активности представляли фигуру, а другие – контур. Мы уже видели, что в зрительной коре есть простые клетки, которые активируются контурами, однако фигура может находиться по обе стороны контура. Проблему решили с помощью двух блоков, каждый из которых «видел» границу фигуры со своей стороны. Такие нейроны были впоследствии обнаружены и в зрительной коре, они называются пограничными клетками.

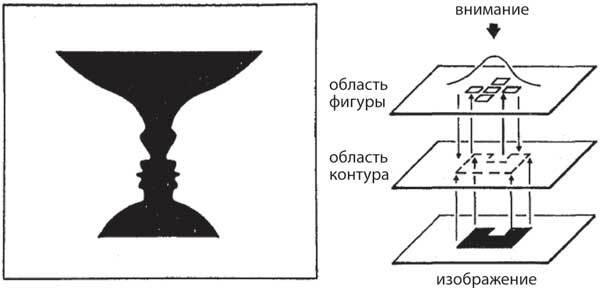
Рис. 7.3. Сетевая модель «фигура-фон». Слева: когда вы фокусируете свое внимание на черном изображении, вы видите вазу на белом фоне. Но когда вы сосредотачиваетесь на белой области, вы видите два лица, смотрящие друг на друга. Вы можете переводить свое внимание с одного изображения на другое, но не можете видеть две картинки одновременно. Справа: два типа элементов, показывающих края объекта и то, является ли пиксель частью фигуры или фона. Входы изображения читаются снизу вверх, а входы внимания – сверху вниз. Внимание реализовано смещением к той области, которая должна быть воспринята в качестве рисунка

Веса в сети были созданы вручную для реализации ограничений (рис. 7.4). Между компонентами фигуры есть возбуждающие связи, между компонентами контура – тормозящие. У пограничных блоков возбуждающие связи с элементами фигуры, на которые они указывают, очерчивая ее, и тормозящие связи с элементами в противоположном направлении. Внимание смоделировано смещением к некоторым элементам фигуры.

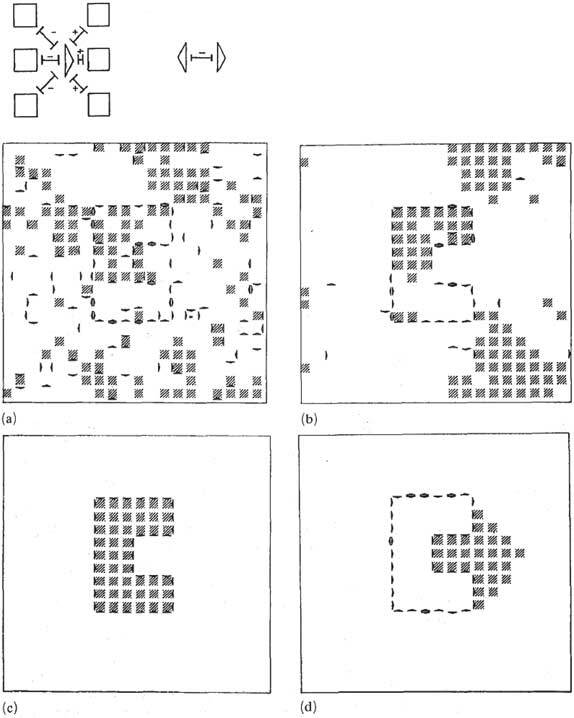
Рис. 7.4. Машина «фигура – фон» Больцмана. Слева внизу: в сети квадраты обозначают фигуру в виде буквы «С», а треугольники – ее контур. Вершина треугольника может быть обращена как к фигуре, так и от нее. Вверху: а) внимание сосредоточено на внутренней стороне «С»; температура была высокой, так что блоки то включались, то выключались; б) по мере падения температуры, блоки на внутренней стороне «С» начинали объединяться при поддержке блоков контура, указывающих внутрь. Блоки, указывающие наружу, не притягивают внимание, и края исчезают по мере того, как температура уменьшается; в) рисунок заполнен, когда внимание обращено внутрь контура; г) фон заполнен, когда внимание обращено наружу

Когда сеть использует для единиц правило обновления Хопфилда, она попадают в локальные энергетические минимумы, которые согласованы в отдельных частях, но не согласованы в глобальных масштабах. Когда к обновлениям добавляли шум, сеть выскакивала за пределы локального минимума, и медленное повышение температуры шума приводило к последовательным решениям на глобальном энергетическом минимуме (рис. 7.4). Поскольку обновления асинхронные и независимые, сеть может быть реализована на многопроцессорном компьютере с массово-параллельной архитектурой и приходить к решениям гораздо быстрее, чем цифровой компьютер, который работает последовательно, выполняя одну операцию за раз.

К этому времени я закончил стажировку в Гарвардской медицинской школе у Штефана Куффлера и получил свою первую работу на кафедре биофизики в Университете Хопкинса. Джеффри Хинтон занял должность преподавателя на факультете компьютерных наук в Университете Карнеги – Меллона. Ему посчастливилось заручиться поддержкой Аллена Ньюэлла, который был открыт для всего нового в развитии ИИ. Питтсбург и Балтимор расположены достаточно близко, и мы могли навещать друг друга по выходным. Мы назвали нашу новую версию сети Хопфилда машиной Больцмана по имени Людвига Больцмана, физика XIX века и основоположника статистической механики – источника инструментов, которые мы использовали для анализа нашей изменяющейся модели нейросети. Вскоре мы обнаружили, что это также мощная обучающаяся машина.

При постоянной «температуре» машина Больцмана приходит в равновесие. В состоянии равновесия происходит нечто невероятное, открывающее дверь, которая, как все считали, останется закрытой навсегда: многослойное обучение нейронной сети. Однажды мне позвонил Джеффри Хинтон и сказал, что только что вывел простой алгоритм обучения для машины Больцмана. Целью обучающего алгоритма было отобразить блоки ввода в блоках вывода, но, в отличие от перцептрона, между ними были блоки, называемые скрытыми элементами (см. блок 4). Представляя пары ввод – вывод и применяя алгоритм обучения, сеть изучила требуемое преобразование. Но простое запоминание пар не было целью; она состояла в том, чтобы правильно классифицировать новые входы, которые не использовались для обучения сети. Кроме того, поскольку машина Больцмана всегда «колеблется», это позволило изучить распределение вероятностей – как часто данный входной шаблон обращается к каждому из состояний вывода. Последнее делает машину Больцмана производящей: после обучения она может создавать новые входные выборки для каждой выходной категории.