К разговору об оценках и моделях

«Люди уверены, что они используют комплексный подход и проявляют изобретательность, вынося свои оценки. Однако сложность и изобретательность большей частью напрасная трата сил – обычно они не помогают превзойти точность простых моделей».

«Даже по прошествии более шестидесяти лет после выхода книги Пола Мила нас по-прежнему шокирует сама мысль о том, что механическое прогнозирование одерживает верх над человеком».

«В оценках столько шума, что «бесшумная» модель эксперта добивается более точных прогнозов, чем собственно эксперт».

Глава 10

«Бесшумные» правила

В последние годы искусственный интеллект (ИИ), особенно на основе методов машинного обучения, позволил компьютерам выполнять множество задач, которые ранее считались доступными только человеку. Алгоритмы на основе методов машинного обучения распознают лица, переводят с одного языка на другой и расшифровывают рентгеновские снимки. Они могут решать вычислительные задачи – например, генерировать управляющие команды для тысяч механизмов одновременно с поразительной скоростью и точностью. Эти алгоритмы выполняют сложные задачи по прогнозированию: предугадывают решения Верховного суда США, определяя, какие из обвиняемых с наибольшей вероятностью будут выпущены под залог, и оценивают, какие из звонков в органы опеки требуют незамедлительного приезда социального работника.

Хотя в наше время, слыша слово «алгоритм», мы подразумеваем компьютерные программы, термин имеет более широкое значение. В словаре алгоритм определяется как «процесс или набор правил, описывающий порядок действий при вычислениях или при решении других задач, в частности с использованием компьютера». Согласно данному определению, простые модели и другие виды механического прогнозирования, описанные нами в предыдущей главе, также являются алгоритмами.

По сути, большинство типов механических подходов к решению задач, от почти смехотворных простых правил до утонченных и непостижимых машинных алгоритмов, превосходят экспертные оценки. И одна из основных – хотя и не единственных – причин этого превосходства состоит в том, что все механические подходы свободны от шума.

Чтобы изучить различные типы подходов на основе алгоритмов и понять, как и при каких условиях каждый из них может быть полезен, мы начнем наш обзор с моделей из главы 9: простых моделей на базе множественной регрессии (то есть линейных регрессивных моделей). От этой отправной точки мы двинемся в двух противоположных направлениях – сначала поищем крайнюю простоту, а затем перейдем к повышенной сложности (рисунок 11).

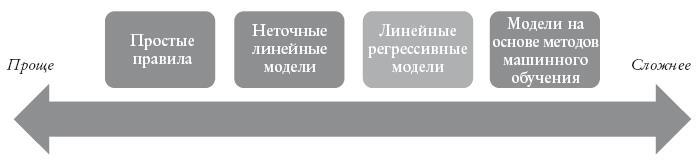
Рис. 11. Четыре типа правил и алгоритмов

Больше простоты: грубые и прекрасные

Робин Доуз был еще одним членом команды из Юджина, штат Орегон, которая в 1960-е и 1970-е годы изучала прогнозирование. В 1974 году Доуз добился прорыва в упрощении задач прогнозирования. Ему пришла на ум поразительная и почти еретическая идея: вместо использования множественной регрессии для определения точного веса каждого прогностического фактора он предложил придать всем им равный вес.

Доуз назвал свою равновесную формулу неточной линейной моделью. Его удивительное открытие состояло в том, что равновесные модели практически так же точны, как и «правильные» линейные модели, и далеко опережают клинические прогнозы¹¹⁴.

Даже сторонники неточных моделей соглашаются, что это утверждение неправдоподобно и «противоречит статистической интуиции»¹¹⁵. Более того, Доузу и его ассистенту Бернарду Корригану вначале пришлось побороться за публикацию своей работы в научных журналах; издатели им попросту не верили. Если вы вспомните пример Моники и Натали в прошлой главе, то, скорее всего, поверите, что одни прогностические факторы более весомы, чем другие. Многие люди, к примеру, придадут большее значение лидерским качествам, чем техническим навыкам. Как тупое, невзвешенное среднее может спрогнозировать чьи-то успехи лучше, чем тщательно вычисленное средневзвешенное значение? Или лучше, чем признанный эксперт?

Сегодня, спустя много лет после прорыва Доуза, так удивлявший его современников статистический феномен хорошо изучен. Как мы уже объяснили ранее в этой книге, множественная регрессия вычисляет «оптимальные» весовые коэффициенты, которые минимизируют квадратичные ошибки. Однако при этом ошибки минимизируются в исходных выборочных данных. Таким образом формула корректирует сама себя, чтобы предугадать всякую случайную флуктуацию в данных. Например, если какие-то из менеджеров в выборке обладают хорошо развитыми техническими навыками, то в случае высоких показателей по другим, не связанным с ними показателям модель преувеличит вес технических навыков.

Проблема в том, что, когда формула применяется вне выборки – то есть для других наборов данных, – присвоенные таким образом веса уже не будут оптимальны. Флуктуации, имевшие место в первоначальной выборке, больше не присутствуют – на то они и случайности; не все менеджеры с хорошо развитыми техническими навыками являются суперзвездами. А в новой выборке уже другие флуктуации, которые формула не может учесть. Истинная мера точности модели – ее приспособляемость к новой выборке, иначе говоря, способность к корреляции с перекрестной проверкой. Действительно, регрессивная модель слишком успешно работает в оригинальной выборке, в то время как при наличии перекрестной проверки корреляция почти всегда ниже, чем она была в исходных данных. Доуз и Корриган сравнивали равновесные модели с моделями на основе множественной регрессии (с перекрестной проверкой) в различных ситуациях. Рассматривался типичный случай: прогнозирование среднего балла в первый год обучения для 90 студентов факультета психологии в Иллинойском университете; использовались десять переменных, имеющих отношение к успеваемости: результаты тестов на выявление способностей, отметки в колледже, различные субъективные оценки ровесников (например, степень экстраверсии), а также самооценка (например, добросовестности). Стандартная модель на основе множественной регрессии показала корреляцию 0,69, а наличие перекрестной проверки ухудшило результат до 0,57 (ПС=69 %). Корреляция равновесной модели со средним баллом осталась примерно такой же: 0,60 (ПС=70 %). Похожие результаты¹¹⁶ были получены и во многих других исследованиях.

Модели с перекрестной проверкой показывают наихудший результат, когда оригинальная выборка слишком мала, поскольку флуктуации в маленьких выборках принимают угрожающие размеры. Доуз обнаружил проблему: используемые в социологических исследованиях выборки обычно настолько малы, что теряется все преимущество так называемого оптимального взвешивания. Недаром статистик Говард Уэйнер снабдил научную статью, посвященную расчету правильных весов, подзаголовком «Нам без разницы»^116а. Или, как говорил Доуз, «нам не нужны¹¹⁷ модели настолько точные, что мы эту точность не можем измерить». Равновесные модели работают хорошо, потому что они нечувствительны к специфике конкретной выборки.

Непосредственные выводы из работ Доуза получили заслуженное признание: вы можете давать эффективные статистические прогнозы, ничего не зная наперед об аналогичных предшествующих результатах. Все, что вам нужно, – это набор прогностических факторов, относительно которых вы можете быть уверены, что они коррелируют с конечным результатом.

Предположим, вам нужно спрогнозировать эффективность работы менеджеров, которым присвоены рейтинги по некоторому количеству параметров, как в примере из главы 9. Вы уверены, что набранные баллы оценивают определенные компетенции кандидатов, однако не имеете данных о том, насколько хорошо они прогнозируют будущий успех. Вы также не можете позволить себе роскошь ждать несколько лет, чтобы отследить успехи большой выборки менеджеров. Однако вы можете взять баллы по семи параметрам, проделать необходимую статистическую работу, чтобы присвоить им равные веса, и использовать результат в качестве прогноза. Насколько хороша эта равновесная модель? Ее корреляция с конечным результатом¹¹⁸ составляет 0,25 (ПС=58 %), что намного превосходит клинические оценки (r=0,15, ПС=55 %) и уверенно приближается к регрессивной модели с перекрестной проверкой. При этом вам не требуется никаких дополнительных данных, которых у вас нет, и никаких сложных вычислений.

Действительно, в равных весах есть «грубая красота»¹¹⁹ – недаром высказывание Доуза стало мемом среди студентов. Заключительная фраза знаменитой статьи, которая ввела в обиход идею, содержала очередное лаконичное резюме: «Вся хитрость в том¹²⁰, чтобы выбрать нужные переменные и правильно их сложить».