Дети монеты
Что меня больше всего впечатляло и озадачивало за мою преподавательскую карьеру, так это человеческая генетика. Я не имею в виду тот неудачный семестр в 2010 году, когда меня вынудили вести биологию у десятиклассников. Нет, я имею в виду самое захватывающее преимущество долговременной работы в школе: знакомство с семьями.

Всякий раз, когда вы преподаете двум родственникам — брату и сестре, кузенам, тете и племяннику одного возраста, вы снова и снова поражаетесь сумбурной природе биологического наследования. Я учил братьев и сестер, похожих друг на друга, словно близнецы, и близнецов, которые были совершенно не похожи друг на друга. Школьные родительские вечера всегда вносят сумятицу в мой разум. От встречи к встрече мое сознание в режиме реального времени смешивает лица матери и отца, сидящих передо мной, и я обнаруживаю, что их ребенок — безупречная работа в «Фотошопе»: его уши и ее глаза, его волосы и ее форма головы. Любые две семьи друг от друга отличаются, но в чем-то все семьи похожи.
Загадки сходства поражают биологов до глубины души. Однако я не биолог, и это могут подтвердить мои ученики. У меня нет секвенатора, нет специальных знаний об интронах и гистонах и (что еще важнее) нет даже никаких догадок на этот счет. Нет, я математик. Все, что у меня есть, — монета, теорема и — в духе «Отважного маленького тостера» — вера в силу выводов из основополагающих принципов.
И, возможно, этого достаточно.
Эта глава затрагивает два, на первый взгляд, не связанных между собой вопроса теории вероятностей. Во-первых, вопрос наследования генов, которому можно посвятить несколько школьных учебников. Во-вторых, вопрос об игре в орлянку, который кажется настолько тривиальным, что едва ли стоит наклоняться, чтобы поднять его с пола.
Можем ли мы соединить эти две области? Может ли однозвучный звон монет выразить всю сложность человеческой расы?
Я намерен ответить «да». И я вполне уверен, что унаследовал эту убежденность от отца.
Окей, начнем с простейшего из двух вопросов: что происходит, когда вы подбрасываете монету?
Ответ: есть два равновероятных исхода, орел или решка. Задача решена!
Хм, вы чувствуете это? Есть особое удовольствие в том, чтобы отвернуться от срочной, трудноразрешимой проблемы реального мира и сосредоточиться на головоломке, до которой никому нет дела. Посмакуйте это чувство. Вот почему некоторые люди становятся математиками.
Ладно, ничего особенного не происходит, если мы подбрасываем одну-единственную монету. Но что произойдет, если мы подбросим пару монет? Вы обнаружите, что равновероятны четыре исхода:
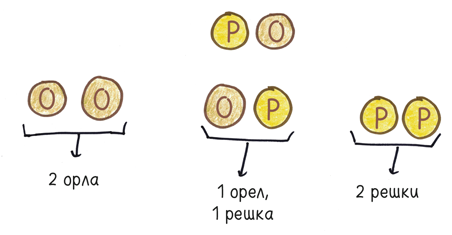
Педант сочтет, что два средних результата отличаются друг от друга: орел и решка не то же самое, что решка и орел. (Представьте, что мы подбрасываем цент и пятицентовик.) Но если вы похожи на большинство игроков в орлянку, то не увидите разницы. Ваш разум сведет оба исхода к одному (один орел, одна решка), и вероятность такого исхода — 50%.
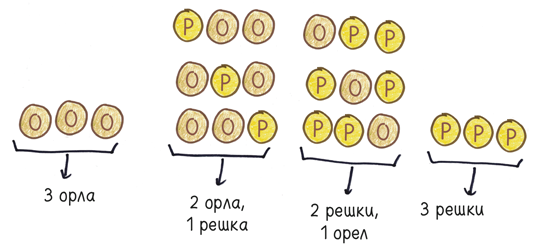
Продолжим: что произойдет, если мы подбросим три монеты?
В общей сложности восемь исходов. Если вы надеетесь, что орел выпадет трижды, есть всего один вариант: каждая монета должна выполнить свой долг, поэтому вероятность этого исхода равна 1 к 8. Но если вы надеетесь на то, что орел выпадет два раза, а решка — один, то есть три варианта — решкой может упасть либо первая, либо вторая, либо третья монета, поэтому вероятность такого исхода равна 3 к 8.
А что произойдет, если мы подбросим четыре монеты, или пять, или семь, или девяносто?
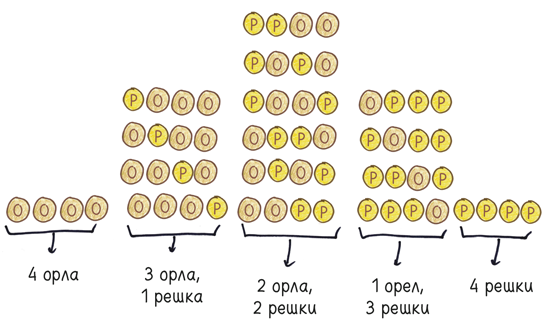
В данном случае мы исследуем семейство вероятностных моделей, известных под названием биномиальное распределение. Ваше единичное событие с двумя равновероятными исходами (орел или решка, победа или поражение, ноль или единица) происходит несколько раз. Это и есть биномиальность. И тогда, изучая эту ветвь математического генеалогического древа, мы наблюдаем две четких тенденции.
Первая: чем больше монет, тем сильнее расцветает сложность. Добавим одну монету, и количество потенциальных исходов увеличится вдвое, от 2 до 4, до 8, до 16. Подбрасывая десять монет, мы рассчитываем на чуть более чем тысячу различных исходов.
Подбросьте 50 монет, и количество исходов возрастет до 250, то есть больше квадриллиона. Эта тенденция агрессивного роста известна под названием комбинаторный взрыв. Линейный рост количества объектов ведет к экспоненциальному росту количества их комбинаций. Горсть монет, при всей своей кажущейся простоте, порождает непостижимое разнообразие.
Вторая тенденция обратная: даже если число вариантов быстро возрастает, доля необычных исходов сильно сокращается. Удостоверьтесь в этом на примере с четырьмя монетами, приведенном выше: есть всего два необычных варианта (все орлы и все решки) против 14 обыкновенных. Чем больше монет мы подбрасываем, тем меньше число необычных вариантов и тем глубже мы увязаем в трясине с практически равным соотношением орлов и решек.
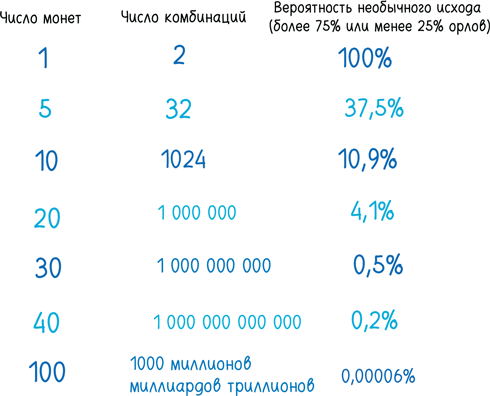
Причина проста. Обычные исходы обычны именно потому, что есть много вариантов получить их. В то же время необычные результаты необычны именно потому, что их редко можно получить.
Предположим, мы подбрасываем 46 монет. Есть всего один вариант, когда все они выпадают орлом кверху.
Но допустим, нас интересуют исходы, когда единожды все-таки выпадает решка — возможно, это первая монета, или вторая, или третья, или четвертая, или пятая… и так далее вплоть до сорок шестой. Таким образом, есть 46 вариаций.
Сколько вариантов с двумя решками и 44 орлами? Еще больше. Решкой кверху могут выпасть первая и вторая монеты, или первая и третья, или первая и четвертая… или первая и последняя… или вторая и третья, или вторая и четвертая, или вторая и пятая… вплоть до второй и сорок шестой. В общей сложности есть более чем 1000 вариаций. Еще теплее! Наиболее вероятный исход — 23 орла и 23 решки — подразумевает восемь триллионов различных вариантов.
Я не экстрасенс, но если вы подбросите 46 монет, то я предвижу, что произойдет одно из двух:
- От 16 до 30 монет выпадут орлом кверху.
- Ваша последовательность будет исторической аномалией, уникальной в опыте всего человечества. Ни один подбрасыватель 46 монет еще не достиг ровно такого результата!
Отчего-то первый результат (серединный) затмевает второй (великолепный и уникальный). Для нас все монеты взаимозаменяемы, поэтому любая примерно сбалансированная последовательность орлов и решек будет казаться нам обычной и забудется, как снежинка во время метели.
Но представьте, что нас интересует структура этой снежинки. Представьте, что каждая последовательность орлов и решек для нас — особый поворот судьбы. Что, если нас тревожит не просто количество, но и конкретная последовательность орлов и решек?

Тогда любая из 70 триллионов возможных комбинаций станет для нас настолько исчезающе маловероятной, настолько вопиюще неожиданной, что ее появление покажется чудом. Она заворожит нас, словно звезда, сорвавшаяся с неба прямо к нам в руки. Эта последовательность 46 орлов и решек будет бесценна, как… ну, новорожденный малыш.
И это подводит нас к сложнейшему из двух вопросов главы: генетике.
Каждая клетка вашего тела содержит 23 пары хромосом. Представьте, что это поваренная книга в 23 томах, инструкция по изготовлению вашего организма, и у вас есть две версии каждого тома: мамина и папина.

Разумеется, у ваших родителей тоже есть по две копии: одна от вашей бабушки, другая от дедушки. Как они решили, какие именно хромосомы передать вам, своей драгоценной горошинке? Предположим, — и здесь я прибегаю к довольно театральному упрощению — они подбросили монету. Орел — вы получаете хромосому от дедушки. Решка — от бабушки.
Ваши родители повторили этот процесс по 23 раза, выбрали 23 тома, и в результате… ну, появились вы.

Исходя из этой модели у каждой семейной пары есть 246, или 70 триллионов, различных вариантов распорядиться своими хромосомами. В отличие от игры в орлянку, здесь детали имеют значение. Я унаследовал от матери густые волосы и тягу к чтению, а от отца — его походку и любовь к ясности. Если бы я унаследовал иную смесь их черт, например отцовские кудри и рост матери (или отсутствие того и другого), я бы стал другим человеком — своим собственным братом.
В наследовании генов орел и решка — не то же самое, что решка и орел.
Эта модель предсказывает различные степени сходства между братьями и сестрами, которые мы можем видеть. Одна крайность — всякий раз монета для младшего брата может выпасть так же, как для старшего. Несмотря на разницу в возрасте, такие братья, по сути дела, будут близнецами.
Другая крайность — ни одна монета не выпадает так, как в предыдущем случае. Тогда братья, словно в какой-нибудь жуткой книге Филиппа К. Дика, по отношению друг к другу будут генетическими чужаками, имеющими на биологическом уровне не больше общего, чем их родители.
Разумеется, обе крайности маловероятны. Скорее всего, у братьев будет примерно половина общих хромосом из 46 — возможно, чуть больше, а возможно, чуть меньше. Согласно нашей биномиальной модели, львиная доля вариантов — от 18 до 28 общих хромосом.
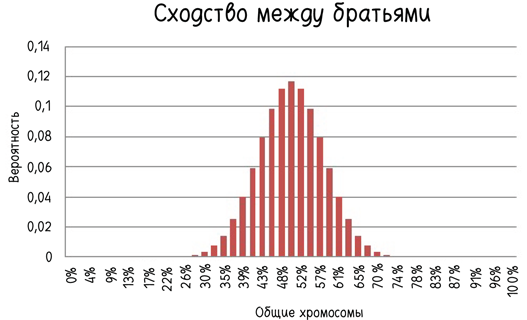
Данные примерно по 800 парам братьев и сестер, собранные Блейном Беттингером и опубликованные в его блоге «Генетический генеалог», показывают, что наш грубый прогноз был чертовски хорошим:
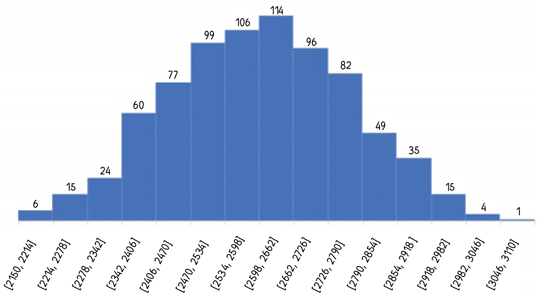
Есть одно возражение. Я не упомянул настолько важный фактор, что не буду осуждать биологов, если прямо сейчас они яростно раздирают эту книгу на клочки. Это кроссинговер, или рекомбинация.
Я утверждал, что хромосомы передаются по наследству неповрежденными и нетронутыми. Это ложь, как и многие вещи, которые я говорил на уроках биологии. Прежде чем происходит выбор каждой версии хромосомы, две хромосомы склеиваются, например обмениваются средней третью. Таким образом, данная хромосома может преимущественно быть дедушкиной, но в ней будет несколько рецептов из бабушкиной поваренной книги.
Кроссинговер происходит примерно дважды с каждой хромосомой. Таким образом, для повышения точности нашей модели мы можем утроить количество монет (потому что два кроссинговера расщепляют хромосому на три части).
Как это влияет на потенциальное количество детей, отличающихся друг от друга? Вспомните: линейный рост количества объектов приводит к экспоненциальному росту числа их комбинаций. Поэтому разнообразие потомков увеличится гораздо больше, чем в три раза. Точнее, от 246 (около 70 триллионов) до 2138 (ошеломляющие 350 дуодециллионов).
Короче говоря, я утверждаю, что у новорожденного младенца много общего с горстью рассыпанных центов. Это не означает, что вы должны присвоить вашему ребенку цену $0,46. Наоборот, уронив на пол 46 центов, вы должны восхищаться, словно родился новый человек.

Знакомясь с семьями, вы думаете, что они смешиваются, словно краски: синий и желтый порождают зеленый. Но это не так. Семьи смешиваются, словно колоды карт, элементы тасуются и перетасовываются, их прячут в рукав, а потом снова выкладывают на сукно. Генетика — это комбинаторная игра: чудесные и неуловимые закономерности сходства между братьями и сестрами можно отследить до исходного комбинаторного взрыва. Подбросьте достаточно много монет, и четкие, несомненные результаты (орел или решка) начнут размываться и перепутываться. Зазубренные края графика становятся столь же плавными и текучими, сколь и само человечество. Таким образом, все мы — отпрыски комбинаторики, потомки перетасованной колоды, дети монеты.

