Игра в кости
От 1 до 7 500 000 000 игроков
Спасибо за покупку игры в кости! Это веселое времяпрепровождение любили все, от простолюдина до тирана, на протяжении всей истории цивилизации, от каменного до цифрового века. Не верьте мне на слово. Просто спросите римских императоров:
Это руководство познакомит вас с основными правилами игры. Игра в кости подразумевает и теорию, и практику в равной мере — тренируйте и ум, и кончики пальцев. Давайте играть!
ЦЕЛЬ ИГРЫ:
Увлечь и позабавить человечество с помощью приспособления, которое выдает результаты, не поддающиеся контролю.
Мы начинаем с класса персонажей, известных под названием «люди». Эти существа любят все контролировать, поэтому они изобрели автомобили, оружие, правительства и центральное кондиционирование. Но они одержимы еще и тем, что находится вне их контроля: пробки на дорогах, погода, их дети и успехи известных парней, которые занимаются спортом за деньги.
В глубине сердца люди хотят противостоять судьбе, держать свое бессилие в собственных ладонях. Так возникают игральные кости — карманные частицы судьбы.
В VI тысячелетии до н.э. племена Древней Месопотамии использовали в качестве игральных костей камни и ракушки. Древние греки и римляне предпочитали овечьи бабки. Индейцы — бобровые зубы, скорлупу грецкого ореха, вороньи когти и сливовые косточки. В санскритском эпосе Древней Индии цари кидали пригоршни орехов бибхитаки. Эти природные игральные кости позволяли резаться в азартные игры, предсказывать судьбу, делить добычу и (вне всяких сомнений) были неотъемлемой частью других ритуалов, от священных до повседневных. Как десерты и послеобеденный сон, идея игральных костей была настолько очевидна и красива, что каждая культура приходила к ней независимо от других.
В наши дни лишь горстка ярых консерваторов играет в «Монополию», бросая бобровые зубы. Цивилизация продвинулась от найденных где попало игральных костей к спроектированным.
А теперь начинается настоящая игра в кости.
Правило №1. Хорошая кость играет честно
Когда вы бросаете игральную кость, вероятность выпадения каждой грани должна быть одинаковой. В противном случае соперники нервничают, становятся подозрительными и перестают приглашать вас на вечеринки, где играют в нарды.
Полезная отправная точка: конгруэнтность. Две геометрические фигуры называют конгруэнтными, если одну можно наложить на другую так, чтобы они совпали. Конгруэнтные геометрические фигуры — неотличимые близнецы, углы и стороны одной равны соответствующим углам и сторонам другой. Таким образом, первая идея проектирования честной игральной кости — убедитесь, что все грани конгруэнтны друг другу.
Звучит отлично… пока не встретишься с курносым дисфеноидом.
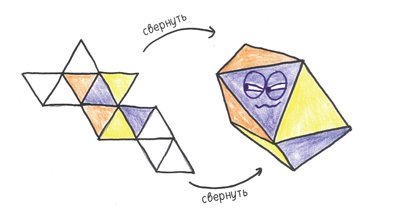
Этот полиэдр, многорылый слепыш, развенчивает наши надежды. Все его 12 граней — идентичные друг другу равносторонние треугольники. Но эту игральную кость нельзя назвать честной.
В некоторых его вершинах пересекаются четыре треугольника, а в прочих — пять треугольников. Когда вы кидаете на стол этого маленького монстра, некоторые грани выпадают чаще, чем другие. Боюсь, что конгруэнтности граней недостаточно.
Нам нужна симметрия.
Говоря простым языком, симметрия означает неуловимое, ласкающее глаз единообразие.
Ее математический смысл гораздо конкретнее: геометрическое действие, преобразующее объект, но не меняющее его сути. Например, у квадратного стола есть восемь видов симметрии:
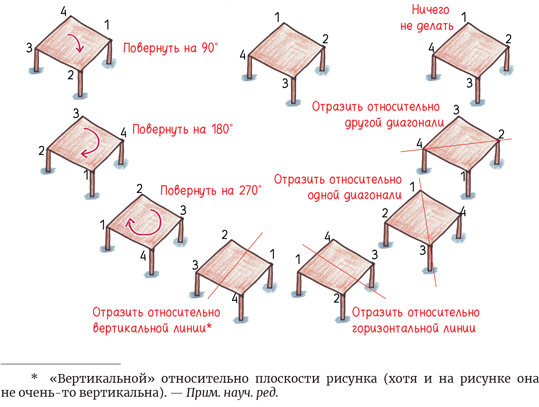
Симметрические отображения не меняют форму стола, однако внимательный анализ показывает, что они меняют местами его углы. Например, поворот на 180º меняет местами противоположные углы: №1 занимает место №3, и то же самое с №2 и №4. Сравните с отражением по диагонали, которое меняет местами углы №2 и №4, но оставляет на своих местах углы №1 и №3. Симметрические отображения игральной кости работают примерно так же: грани меняются местами, но форма остается неизменной.
Симметрия предлагает верный путь к честной игре. Просто выберите геометрическое тело, достаточно симметричное, чтобы все грани можно было поменять местами.
Например, бипирамида. Возьмите две идентичных пирамиды и приклейте их основания друг к другу. Правильная комбинация поворотов сможет поменять любую треугольную грань на любую другую, и это означает, что все грани геометрически эквивалентны и игральная кость честная.
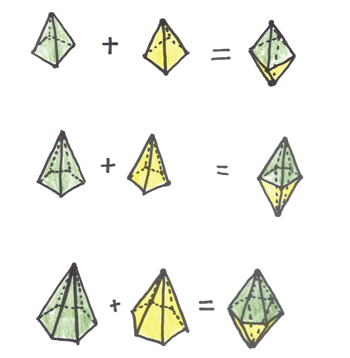
Другой пример: трапецоэдр. Он выглядит как бипирамида с изящной резьбой по экватору, которая превращает треугольники в четырехугольники, похожие на воздушных змеев.
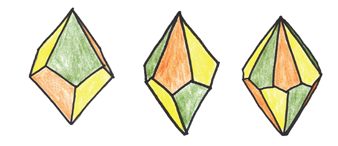
Вы можете сделать бипирамиду или трапецоэдр с любым количеством граней: 8, 14, 26, 398. Теоретически любая из этих игральных костей обеспечит честную игру, грани будут выпадать с одинаковой вероятностью. Наверное, вы думаете, что мы решили проблему. Игра в кости окончена, да? Не так быстро! Люди гораздо капризнее. Недостаточно, чтобы игральная кость была честной…

Правило №2. Хорошая игральная кость выглядит прелестно
Мы встретились с номинантами на роль игральной кости, которые (1) легко поддаются определению, (2) дают справедливые результаты и (3) носят потрясающие греческие и латинские именами. Однако эти многообещающие модели — стопроцентные исторические неудачники, провалившиеся кандидаты в президенты мира случайности. Насколько я знаю, ни одна цивилизация, играющая в кости, не пользовалась бипирамидой и есть всего один пример использования трапецоида: теневое сообщество фанатов настольной игры «Подземелья и драконы», где используют десятигранный трапецоид (d10).
Человечество, почему ты так привередливо? Как ты можешь отвергать прекрасные формы и разбрасываться честными игральными костями?
Киньте на стол тощую бипирамиду, и вы увидите, в чем проблема. Она не кувыркается. Уравновешенная двумя заостренными концами, она почти что катится, словно рулон бумажных полотенец, заваливаясь влево-вправо и повышая шансы то одной, то другой группы граней. Ее равновесие после остановки хрупко; один неосторожный вздох — и она перевернется на другую грань. Это не рецепт веселой игры в парчиси, а гарантия семейного скандала со взаимными упреками.

У наилучшей игральной кости симметричны не только грани. Нужно, чтобы все ее компоненты было симметричными. И если вы страстный поклонник многогранников, то вы понимаете, что это значит.
Платоновы тела!
Из всех трехмерных геометрических фигур с прямыми ребрами платоновы тела самые совершенные. Можно поменять местами любые две грани, угла или ребра — симметрия настолько великолепна, что даже закоренелый циник не усомнится в их выдающейся честности.
Есть всего пять платоновых тел, ни больше и ни меньше. И каждый бог этого геометрического пантеона снизошел на землю в образе игральной кости.
1. Тетраэдр — пирамида, состоящая из равносторонних треугольников. За 3000 лет до н.э. обитатели Древней Месопотамии кидали игральные кости в виде тетраэдра во время Царской игры города Ур, предшественницы игры в нарды.
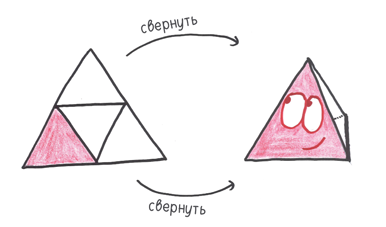
2. Куб — призма с квадратными гранями. Простой, устойчивый, легко изготовляемый, он остается самой популярной формой игральных костей за всю историю человечества. Древнейший экземпляр — куб из обожженной глины, найденный на раскопках в Северном Ираке, — датируют 2750 годом до н.э.
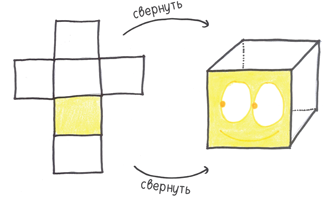
3. Октаэдр — особая бипирамида, грани которой представляют собой равносторонние треугольники. Игральные кости в виде октаэдров были найдены в нескольких египетских гробницах.
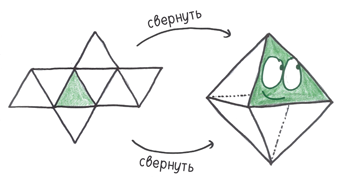
4. Додекаэдр — радующий глаз драгоценный камень с 12 гранями в виде правильных пятиугольников. Он помогал прорицать судьбы в XVI веке во Франции. Сегодня астрологи наслаждаются соответствием 12 граней и 12 знаков зодиака.
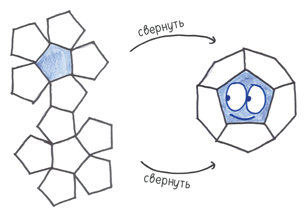
5. Икосаэдр — многогранник из 20 равносторонних треугольников. Это неотъемлемый элемент игры «Подземелья и драконы», но он гораздо популярнее в гаданиях. Так называемый шар вопросов и ответов представляет собой икосаэдр, плавающий в воде. Встряхните его — и это платоново тело предскажет ваше будущее.
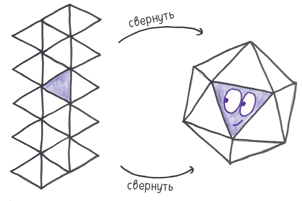
Платоновы тела — козыри игры в кости. Невозможно представить их без небесного хора, поющего на заднем фоне. Однако этот элитный пантеон из пяти элементов слишком малочислен. Они обеспечивают 4, 6, 8, 12 и 20 случайных исходов… но других вариантов нет.
Имеет смысл расширить горизонт. Почему бы не выбрать дизайн, взламывающий парадигму, свежий, инновационный путь, способный обеспечить любое количество равновероятных результатов?
Спойлер: легко сказать, трудно сделать.

Правило №3. Хорошая игральная кость работает повсеместно
Одна из альтернатив — продолговатая игральная кость. Не тревожьтесь о том, имеют ли все грани равные шансы, и сконструируйте вытянутую призму.
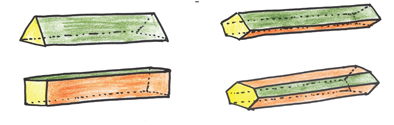
Эти игральные кости работают не потому, что все грани выпадают с равной вероятностью, а потому, что две из них не выпадают никогда. Продолговатая игральная кость играет честно, выглядит красиво и позволяет выбрать любое количество возможных исходов. Так почему они не слишком популярны?
Ну… они слишком далеко катятся.
В то время как платоновы тела отплясывают на столе, словно на танцплощадке, подпрыгивая там и сям, продолговатая игральная кость катится в одном направлении. Вы должны расчистить для нее целую дорожку для боулинга. Каким же самомнением должны обладать игральные кости, чтобы расстилать перед ними ковровую дорожку?
Запишем на грифельной доске еще один математический принцип: непрерывность.
Киньте вашу продолговатую игральную кость и ждите, пока она не остановится. (И ждите, и ждите…) Как мы можем видеть, две грани не выпадают никогда. Но представьте укороченную игральную кость, не такую уж и продолговатую. Чем она короче, тем выше вероятность выпасть двум боковым граням. Чем дальше вы укорачиваете вашу игральную кость, тем больше она уподобляется монете, и грани меняются ролями. Монета почти никогда не падает на ребро — выпадает или орел, или решка.
В процессе укорачивания есть критическая точка, когда все грани будут выпадать с равной вероятностью. Это и будет честная игральная кость.
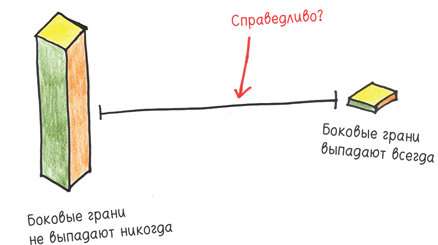
Теоретически вы можете проделать этот фокус с любым многогранником и отыскать геометрические фигуры, которые выглядят чудаковато, но тем не менее обеспечивают справедливую игру. Но где же они? Почему в разделе новинок в магазинах не продаются изящные игральные кости, которые хоть и диковатого вида, но все равно хороши для игры, — фантастический антипод жульнических игральных костей?
Дело в том, что требуется слишком чувствительная настройка. Игральная кость честна на поверхности из твердой древесины? Да, а на граните — нет. Игральная кость определенного размера честна? Да, но при удвоении размера уже нет. Этот бросок костей честен? Да, но другой бросок может быть и не честен, все зависит от силы и скорости вращения. Если вы меняете одно из условий, сколь угодно непредвиденных, вы меняете физические данные. Такие кости вечно будут связаны со слишком специфическими обстоятельствами их появления на свет. Людям нужны компактные выносливые кости, а не капризные примадонны.

Правило №4. Хорошую кость легко кидать
Допустим, нам нужно случайным образом выбрать одну из 26 букв алфавита. У икосаэдра граней слишком мало. Бипирамида комично покачивается. Продолговатая игральная кость укатывается невесть куда, как беглая фрикаделька. Исключив эти варианты, мы попадаем в тупик. Неужели нет ни одного способа решить простую задачу и выбрать одну букву случайным образом? Разумеется, есть. Просто подбросьте пять монет. Возможны 32 равновероятных варианта. Сопоставьте по букве каждому из 26 первых вариантов, а если выпадут оставшиеся, бросьте монеты снова.
Эта процедура подходит для любого сценария рандомизации. Скажем, мы хотим выбрать произвольное слово из трилогии «Властелин колец». Есть около 450 000 слов на выбор. Подбросьте 19 монет — это даст больше 500 000 равновероятностных вариантов. Поставьте в соответствие каждому слову одну комбинацию. Если выпали незадействованные комбинации, подбросьте монеты снова.

Черт, даже не нужно брать 19 монет. Просто подбросьте одну монету 19 раз.
По этой логике любую игральную кость может заменить одна-единственная монета. Но все-таки сложно себе представить наплыв посетителей в такое казино в Лас-Вегасе, где на столах для игры в крэпс нет ничего, кроме монет, а рулетка основана на подбрасывании цента.

Проблема очевидна: эти системы слишком сложны. Ужасно неудобно записывать последовательность бросков, искать результат в сопоставительной таблице, а время от времени (в случае необходимости) повторять все заново. Вам нужна одна-единственная игральная кость. Без единой лишней грани и без инструкции по применению.
Этот принцип в чем-то отменяет чистую математику. Например, вы можете обеспечить четыре исхода с помощью простого кубика. Просто пометьте две грани значком «бросай снова». Но этот подход раздражает. Лишние грани? Это неэлегантно. Если вы готовите пирог для четырех друзей, вы никогда не станете резать его на шесть частей и выбрасывать две лишних.

Подозреваю, именно поэтому фанаты «Подземелий и драконов» бросают четырехгранную игральную кость. Я воспринимаю это как знак отчаяния, потому что из всех платоновых тел в истории человечества тетраэдр наименее популярен. Опять-таки любому ясно почему: он приземляется гранью вниз, а не гранью вверх. Это кажется неестественным, как будто нужно угадать именно то число, которое вы не загадывали.
На протяжении тысячелетий люди чурались тетраэдра, предпочитая игральные кости с параллельными друг другу гранями, чтобы каждая «нижняя» грань соответствовала одной «верхней». Математикам до этого нет дела. Но музыку заказывают обычные люди.


Правило №5. Ее сложно держать в узде
Помните высшее предназначение игральных костей? Они позволяют человеческому телу установить контакт с высшими силами: случайностью, кармой, судьбой, волей богов. Благодаря игральным костям существуют мозговые штурмы, азартные игры, гадания и другие глубинные проявления нашей человеческой сущности.
Поэтому, естественно, люди пытаются жульничать.
Один путь: манипулировать внешним видом игральной кости. Например, незаметно наращивать ее, чтобы она приобретала форму кирпича. Или создать грани с небольшими выпуклостями (так они будут выпадать реже) или вогнутостями (так они будут выпадать чаще). Можно покрыть некоторые грани упругим материалом или, наоборот, отшлифовать их наждаком, чтобы они выпадали чаще. Эти фокусы старые, как руины. Я говорю в буквальном смысле: жульнические игральные кости с подпиленными углами были обнаружены в Помпеях.
Другой путь: осуществлять манипуляции внутри игральной кости. «Ловушки» — это игральные кости с двумя скрытыми полостями; правильное движение сместит сгусток жидкой ртути из одной полости в другую, меняя степень вероятности выпадения граней. (Если вы не любите ядовитые металлы, используйте воск, который плавится при температуре чуть ниже температуры человеческого тела.) Другая схема: когда были популярны деревянные игральные кости, шулеры выращивали небольшие деревья, надрезали ветви, закладывали мелкие камушки и ждали, пока разрез затянется. Затем они выстругивали игральную кость с этой невидимой добавкой. Эта мошенническая работа требует не только невероятного терпения, но и навыков выдающегося ботаника.


Третий подход: перенумеровать грани. У обычной игральной кости сумма чисел на противоположных гранях равна семи. (Пары 1 и 6, 2 и 5, 3 и 4.) В игральных костях под названием «чечетка» (taps) некоторые числа продублированы, и на противоположных гранях расположены 6 и 6, 5 и 5, 4 и 4. С любого ракурса ваш противник будет видеть всего три грани, поэтому не заметит подвоха.
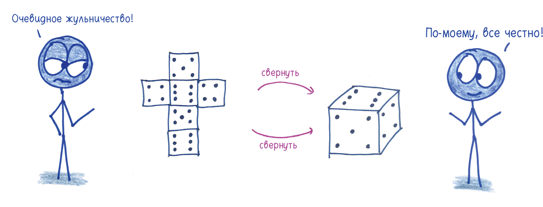
Хотя подобные мошеннические методы нацелены на игральные кубики, эта форма игральных костей не самая уязвимая. Просто самая популярная. Очевидно, что в крэпс можно выиграть больше денег, чем в «Подземелья и драконы».

Правило №6. Хорошая кость — наш вечный гость
Суть игры в кости, как и многих других игр, состоит в том, что в ней нет никакой необходимости. Мы живем в XXI веке. Я добираюсь на работу с помощью реактивного ранца и улетаю в отпуск на крылатом автомобиле. Ладно, я пошутил, но зато я ношу в кармане полмира в виде 140-граммового компьютера. Технологии делают всех нас устаревшими, в том числе работяг, которых называют игральными костями. Смотрите: я хочу оторваться от этого текста и смоделировать миллион бросков игрального кубика в Microsoft Excel. Я дам вам знать, сколько времени это займет.
Окей, готово. Потребовалось около 75 секунд. Вот результаты:
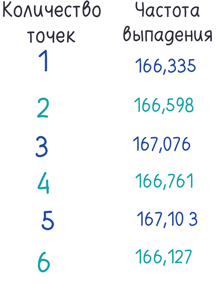
Мало того, что компьютерная генерация случайных чисел быстрее и проще, чем кидание пластикового кубика на стол, она еще и подразумевает более высокую степень случайности. Владельцы казино могут выбросить все рулетки и столы для крэпса: их цифровые заменители будут опережать доисторические генераторы случайных чисел семимильными шагами.
Но разве это будет весело?
Игральные кости созданы для того, чтобы трогать их руками. Первый раз, когда я сыграл в «Подземелья и драконы» (на самом деле первый и последний), я увидел кое-что более завораживающее, чем все орки и маги: зоккиэдр, стогранную игральную кость. Представляете? Сто граней! Игральная кость, которая катится полминуты, прежде чем остановиться! Я знал, что две десятигранные игральные кости (одна для десятков, другая для единиц) удобнее для игры и честнее, чем бритый бугорчатый мячик для гольфа Лу Зокки. Но мне было все равно. Я хотел кидать этот стогранник.

Древние греки, должно быть, чувствовали тот же соблазн, когда кидали надпяточную овечью кость под названием астрагал. Они нумеровали четыре грани странным образом (1, 3, 4 и 6) и бросали пригоршню костей. Единица называлась «псы»: худшее, что можно себе вообразить. Лучший исход назвался «Афродита» (шестерка или другая грань, смотря кого вы спросите). Астрагалы не были честными; они были лучше. Это были частицы скелета в человеческой руке, предсказывающие судьбу. Когда Юлий Цезарь пересек Рубикон, рубеж между закатом Римской империи и зарей Римской республики, он сказал: «Alea iacta est». Жребий брошен.
Игра в кости, я так подозреваю, никогда не исчезнет. Эти кости вошли в нашу плоть и кровь. Просто следуйте этим шести правилам:
Хорошая кость
играет честно,
выглядит прелестно,
работает повсеместно,
ее легко кидать,
но сложно в узде держать.
Хорошая кость —
наш вечный гость.

