Метод 4. Через Lifetime и ARPU, сложный способ

Формула метода точно такая же:

LTV = Lifetime * ARPU

Но Lifetime тут считается немного сложнее и получается намного точнее. Вспомним, как выглядит график Retentio n:

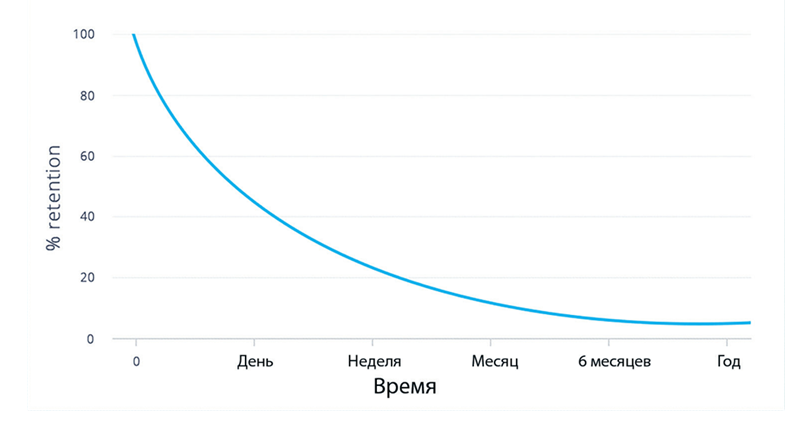
Дело в том, что Lifetime – это площадь фигуры под графиком Retention, иначе говоря – интеграл от Retention по времени.

Но прежде чем считать интеграл, надо построить саму функцию Retention. В этом случае вам предстоит смоделировать эту Retention самостоятельно и по модельному значению отвечать на интересующие вас вопросы.

О моделировании Retention вы можете подробно прочитать в главе 3. Вернитесь к ней и перечитайте тот сложный текст про выбор оптимальной функции.

И возвращайтесь сюда снова.

…Итак, Retention мы смоделировали. Это еще не конец задачи, но мы уже близко. Дальше по-прежнему можно выбрать сложный или простой метод.

Сложный метод заключается в нахождении интеграла от функции Retention.

Напомним, что:

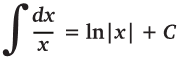
Простой же метод заключается в том, чтобы, пусть и примерно, поделить кривую Retention на сегменты в зависимости от значения Lifetime. Например, на пользователей, ушедших через день, проживших в приложении от 2 до 7 дней, от 8 до 30 дней, от 1 до 3 месяцев, свыше 3 месяцев. Чем больше сегментов, тем лучше. Для каждого сегмента посчитать по таблице Retention процент пользователей (вес сегмента), относящихся к нему, а затем посчитать средневзвешенный Lifetime по всем сегментам.

Но какой бы метод вы ни выбрали, вы столкнетесь с вопросом, до какого момента считать LTV (в случае с интегралом это будет правый край области интегрирования, в случае с суммой – количество дней в последнем сегменте). И здесь вновь существует два метода решения: простой и сложный.

Простой метод заключается в том, что правый край задается экспертно.

Обычно это происходит так:

– А давайте возьмем полгода!

– Почему?

– А почему бы и нет?

– Хорошо, давайте полгода.

Сложный метод заключается в использовании дисконтирования и нахождении ставки дисконтирования WACC.

Признайтесь, вы не ожидали увидеть здесь финансовую математику? Дело в том, что тысяча долларов сейчас и тысяча долларов завтра – это разные суммы. Завтрашняя тысяча долларов сегодня будет равна девятистам долларам или около того, в зависимости от выбора ставки дисконтирования.

Формула такова:

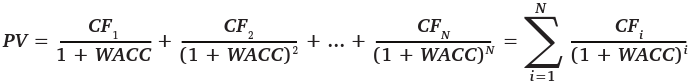
Здесь PV (Present Value) – текущая стоимость будущих денег, CFi – деньги, которые вы получите через i временных периодов, WACC (Weighted Average Cost of Capital) – та самая ставка дисконтирования.

Как ее найти? Обычно WACC делают равной фактической рентабельности капитала в среднем по фирме. Также можно приравнять ее к желаемой рентабельности капитала, либо к рентабельности капитала альтернативных проектов. Если вы не поняли этот абзац, спросите у своих финансистов, они наверняка знают WACC вашей компании.

Итак, зная WACC, вы сможете дисконтировать будущие временные потоки, а следовательно, в качестве правого края интегрирования выбрать хоть бесконечность. Дело в том, что добавление WACC делает из вашей суммы (или из вашего интеграла) бесконечно убывающую последовательность, у которой можно найти сумму.

Будем считать, что Lifetime мы посчитали. Теперь же считаем ARPU (Revenue/DAU), умножаем ARPU на Lifetime и получаем LTV.

Плюсы метода:

1. Точность. Lifetime рассчитан очень точно, погрешность в нем минимальна.

2. Побочный эффект от расчета такого метода – бонусом вы получаете еще и прогноз Retention на сколько угодно дней.

3. Возможность посчитать LTV для каждого сегмента в отдельности.

Минусы метода:

1. Сложно считать, хотя опытный аналитик при наличии всех данных посчитает вам LTV за пять минут.

2. Вновь предположение о неизменности ARPU во времени. Можно немного перестраховаться и взять в расчет не ARPU за один день, а среднедневной ARPU за Lifetime, это увеличит точность.

Метод 5. Накопительный ARPU, или Top Down

Второе название метода взято из материала Wooga, что дает +10 к доверию к данному методу. Из этого же материала взята и картинка:

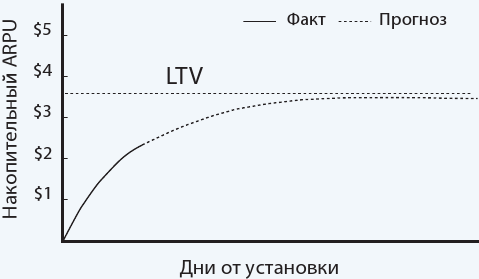
Поясним. Допустим, к вам в проект пришла группа новых игроков, и вы стали за ней следить. Вы замеряете, сколько денег принес вам в среднем один игрок из этой группы за 7 дней, за 14, за 28 и т. д. То есть, по сути, вы переходите от обычного ARPU к накопительному за N дней.

Ну а зная Cumulative ARPU за 7, 14, 28 и т. д. дней, мы вновь сможем построить математическую модель кривой, которая будет прогнозировать значения Cumulative ARPU за сколько угодно дней. Будем искать уравнение кривой вида:

F(t) = A + ln(t + B)

где t – количество дней от первого визита пользователя, F(t) – будущее уравнение, A и B – коэффициенты модели.

Вновь рассчитываем сумму квадратов отклонений и минимизируем ее за счет подбора оптимальных значений коэффициентов A и B.

Если же у вас есть больше значений Cumulative ARPU (скажем, за 60 и 90 дней), то можно добавить в уравнение дополнительные слагаемые вида C*t или D/t, это может повысить точность. Ну и в целом – здесь нет одного уравнения, гарантированно дающего минимальное отклонение. Экспериментируйте с видом уравнения!

Путем нескольких итераций вы таки получите уравнение, которое вас устроит. Теперь, подставив в это уравнение нужное вам значение t, вы получите Cumulative ARPU(t), что по сути и будет равняться LTV.

Как выбрать значение t для расчета LTV?

1. Во-первых, можно взять Lifetime.

2. Во-вторых, можно вновь задать это t экспертно.

3. В-третьих, можно вернуться к дисконтированию и добавить в получившееся уравнение знаменатель 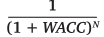. В этом случае рано или поздно на графике станет намечаться асимптотическое значение (как на картинке выше – примерно $3,70, выше которого LTV быть не сможет. Вот это значение и берите).

Итак, мы рассмотрели множество методов расчета LTV, которые, как вы могли заметить, упорядочены от наименее точного к наиболее точному. Выбирайте тот метод, который вам по душе, рассчитывайте свою LTV и принимайте правильные решения.

А теперь – главное правило LTV: делите пользователей на сегменты и считайте LTV каждого сегмента в отдельности. Это даст вам и более высокую точность, и больше поводов для принятия правильных решений по вашему продукту.