Как можно улучшить удержание

– Как говорилось ранее, первая сессия во многом определяет последующее поведение пользователя, и именно в это время нужно как можно быстрее донести до него суть приложения и дать понять, зачем игроку возвращаться. Для этого можно использовать туториал, который наглядно продемонстрирует пользователю функционал продукта.

– Иногда, чтобы пользователи возвращались в проект, им нужно напоминать об этом, используя различные уведомления: пуши, почтовые сообщения и тому подобное.

– Бонусы и подарки, которые пользователь будет периодически получать в процессе работы с приложением, могут способствовать его интересу к продукту и влиять на желание снова в него зайти.

– Можно поддерживать интерес пользователя, постепенно открывая ему новый контент, регулярно ставя цели и задачи.

– Способствовать вовлеченности может деление общего пути к цели на этапы, чтобы пользователь ощущал прогресс и получал удовольствие от достижения или выполнения каждого шага.

– Связь с социальными сетями и взаимодействие с друзьями в рамках продукта создаст большую привязанность и заинтересованность.

– Еще увеличить удержание можно следующим способом: сначала изучить поведение пользователей, которые остались в проекте (их сессии, последовательность действий, использование функционала), а затем провести этим путем новых пользователей.

Удержание – одна из самых важных метрик продукта, поскольку она определяет размер аудитории и возможность роста компании, говорит о первом впечатлении пользователя о продукте и определяет, сколько в среднем времени он проведет в приложении за свою «жизнь», что напрямую влияет на доход. Поэтому удержание относится к тем метрикам, которые необходимо постоянно контролировать и улучшать.

Повторяющееся удержание также характеризует интерес пользователей к проекту и показывает, когда они уже больше в него не вернутся, благодаря чему позволяет рассчитать такие показатели, как отток и Lifetime.

Однако зачастую повторяющееся удержание может дезинформировать разработчика, сформировав положительное впечатление. Ведь его график убывает более плавно, а сами значения часто намного выше классического удержания, что может быть критично для приложений, пользоваться которыми в идеале должны каждый день.

Поэтому для принятия взвешенных решений при анализе возвращаемости пользователей стоит обращать внимание на оба вида удержания.

Как моделировать удержание

График показателя удержания пользователей (Retention) имеет схожий вид и для веб, и для мобильных приложений, а также для интернет-магазинов и многих офлайн-продуктов:

– в первые дни (недели, месяцы) он резко падает: пользователи не успевают пройти обучающий этап (онбординг) и не остаются в проекте;

– затем те, кто все же остался, понемногу отпадают, но уже не с такой скоростью, как в самом начале;

– наконец, затем, когда база пользователей уже сформирована, график выходит на плато, которое лишь едва снижается, и чем больше прошло времени, тем больше график похож на горизонтальную линию.

Графически Retention выглядит примерно так:

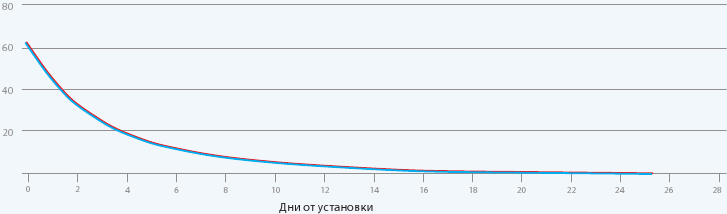
Такую кривую еще называют «кривой забывания» (forgetting curve), потому что ею же описывается процесс забывания человеком полученной информации.

Иногда может возникнуть следующая ситуация: у вас есть значения удержания за какие-то фиксированные периоды (1 день, 7 дней, 30 дней), и вы хотите узнать значения показателя за промежуточные периоды (6 дней, 14 дней, 23 дня) или после них (35 дней).

Это может пригодиться, если вы хотите прогнозировать Lifetime, или LTV (Lifetime Value), а также просто планируете, сколько из ныне активных пользователей останутся таковыми в будущем.

Как быть в этом случае?

Мы умышленно выбрали бесплатные и общедоступные инструменты для решения задачи, чтобы вы впоследствии могли сделать то же самое самостоятельно:

– Open Office, а именно его электронные таблицы и «Решатель» (Solver) во вкладке «Сервис»;

– «Нелинейный решатель», который нужно поставить отдельным бесплатным плагином.

Мы будем пользоваться механизмом аппроксимации, то есть приближением фактических значений математическими формулами. Делая аппроксимацию, важно, во-первых, выбрать правильную функцию (которая изгибалась бы в нужных местах) и верно подобрать ее коэффициенты, чтобы разница между моделью и фактом была минимальной.

Итак, какой же из функций можно аппроксимировать Retention?

На ум (тем, кто заканчивал школьный курс математики) приходит гипербола, и это верная ассоциация.

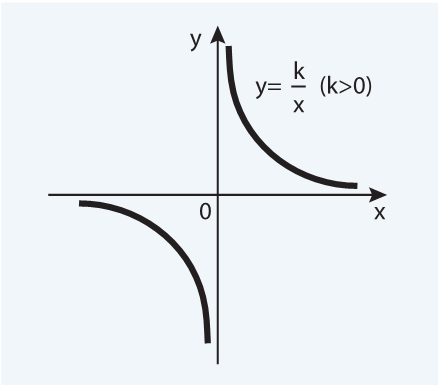
Рассмотрим несколько гиперболических уравнений (X в уравнении означает номер периода: дня, недели или месяца). Начнем с простого уравнения гиперболы A/X, затем будем усложнять его, добавляя различные коэффициенты:

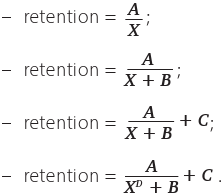
A, B, C, D – коэффициенты, которые нам предстоит найти.

Наша задача: выбрать оптимальное из этих уравнений. Итогом каждого из уравнений будет отдельная кривая, мы будем сравнивать эту модельную кривую с фактическими значениями (которые, надо сказать, не всегда идеально вписываются в модель) и выберем ту из кривых, которая лучше повторяет факт.

Критерием будет минимум суммы квадратов отклонений (что означает, что мы воспользовались методом наименьших квадратов) между фактическими и модельными значениями.

В Excel это делается с помощью СУММКВРАЗН (SUMXMY2). В Open Office эта функция нами не обнаружена, но это не проблема: рассчитываем в отдельном столбце отклонения (просто как разность между модельными и фактическими значениями), возводим их в квадрат, а затем суммируем квадраты отклонений.

Для оптимизации нам пригодится Solver. Притом, учитывая и квадраты отклонений, и гиперболический вид функции, решатель нужен именно нелинейный.

Здесь и далее мы пользовались поочередно DEPS Evolutionary Algorithm и SCO Evolutionary Algorithm, за стартовые данные новой итерации брали значения коэффициентов, полученные на предыдущей итерации. Процесс заканчивался тогда, когда сумма квадратов отклонений с новой итерацией уменьшалась не более чем на 0,01.

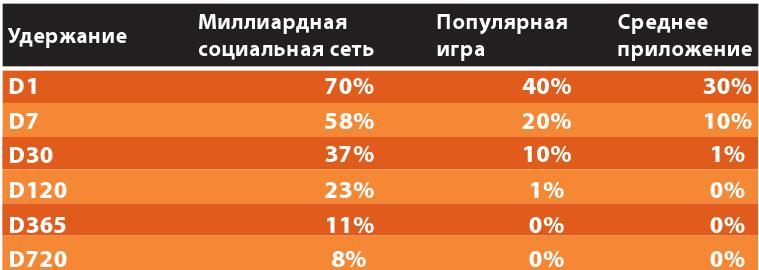
Возьмем за исходные данные показатели удержания неназываемого проекта за 28 дней. По горизонтали – дни в игре, по вертикали – проценты Retention.

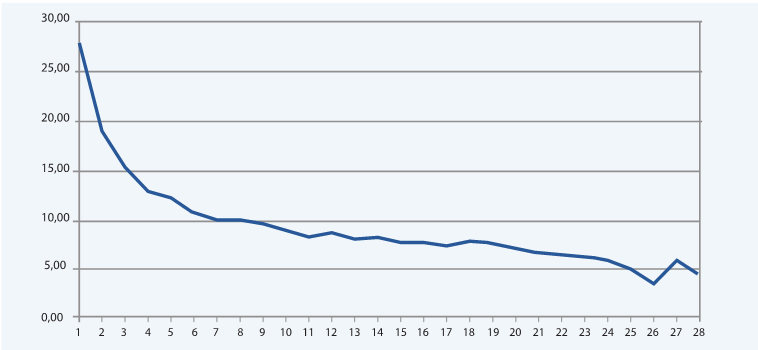
Как видно из графика, данные далеко не идеальны, и для нашей задачи это отлично подходит. Редко на практике вы получаете в руки идеальные данные, а задачу решать все равно надо.

Будем пытаться для каждой из выбранных функций подобрать такие значения коэффициентов, чтобы построить кривую, как можно более близкую к исходным данным. Подбирать будем такие значения, которые по методу наименьших квадратов дадут нам максимальное сходство нашей модели с фактическими значениями.

Вот что получается:

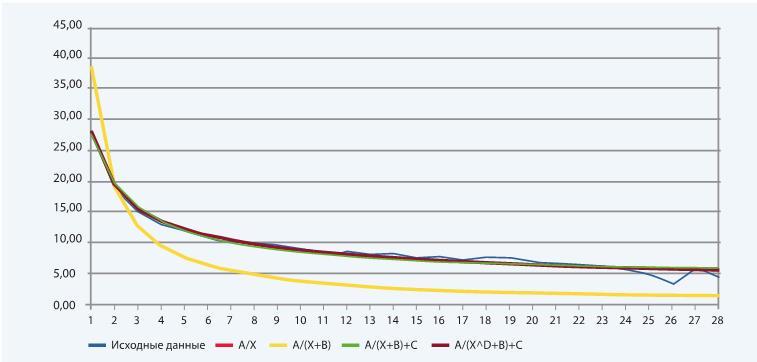
Как видно, желтая 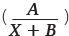и красная 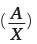линии совпали, но от исходной кривой они очень далеки.

А вот зеленая 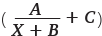и бордовая 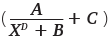линии довольно точно повторили исходную кривую.

При этом бордовая линия, если судить по сумме квадратов отклонений, повторяет стартовые данные точнее всего:

Мы смотрим на то из уравнений, где сумма квадратов отклонений минимальна.

Таким образом, мы прощаемся с уравнениям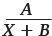и и 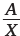и идем дальше.

Если обратить внимание на кривую, то видно, что с каждым днем она меняется все меньше. Нам это напомнило логарифмическую кривую, и мы подумали: а что если вместо X в уравнение подставить LN(X), не улучшит ли это наши результаты?

Поэтому следующим шагом давайте сравним результаты лучшей функции с X и LN(X). Единственное, в одном из случаев добавим под логарифм коэффициент E:

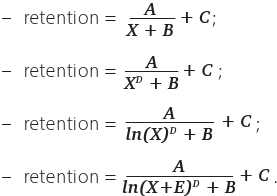
Визуально все четыре кривые справились достаточно неплохо, однако давайте все же рассмотрим квадраты отклонений:

Какие выводы можно сделать?

– Лучше всего аппроксимируют кривые с четырьмя и пятью переменными.

– Замена X на LN(X) пусть и немного, но улучшает аппроксимацию.

На этом этапе мы прощаемся с кривой 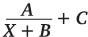. Она не выдержала конкуренции.

Остались три кривые, однако неизвестно, как они работают на длинных дистанциях. Мы тестировали их лишь на первых 28 днях. Вполне вероятен случай, что если вместо X подставить большое значение (скажем, 365), то они уйдут в минус, что невозможно по определению Retention.

Поэтому, раз уж мы определили трех финалистов, давайте следующим этапом протестируем, как они могут справляться с более долгосрочным Retention.

Мы просто взяли несколько примеров долгосрочного Retention из интернета и протестировали наши кривые на каждом из них:

– за 90 дней;

– за 540 дней (18 месяцев);

– за 720 дней.

Пример про 720 дней рассмотрим графически.

Данные были взяты из статьи How to measure the success of your app, и в данном случае мы пытались повторить приведенную статистику по удержанию в социальной сети.

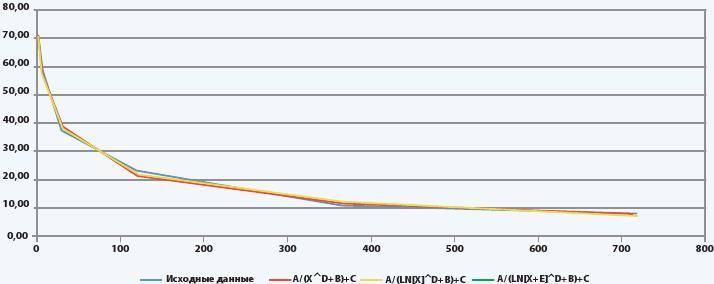
Видно, что все три кривые хорошо справились с аппроксимацией, однако красная линия немного более выдается на фоне синей – отклонение у нее максимальное.

Теперь делимся результатами по всем трем примерам (напомним, чем меньше сумма квадратов отклонений, тем лучше):

Если бы это был чемпионат, то победила бы последняя кривая. Однако, согласитесь, ее преимущество не так явно, особенно учитывая, как мало отличаются друг от друга значения суммы квадратов отклонений. Поэтому победителями (как на детском празднике) мы признаем все три кривые, и все три кривые мы можем рекомендовать для аппроксимации Retention.

Также хотелось бы рассказать про значение каждого из коэффициентов на примере функции .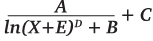

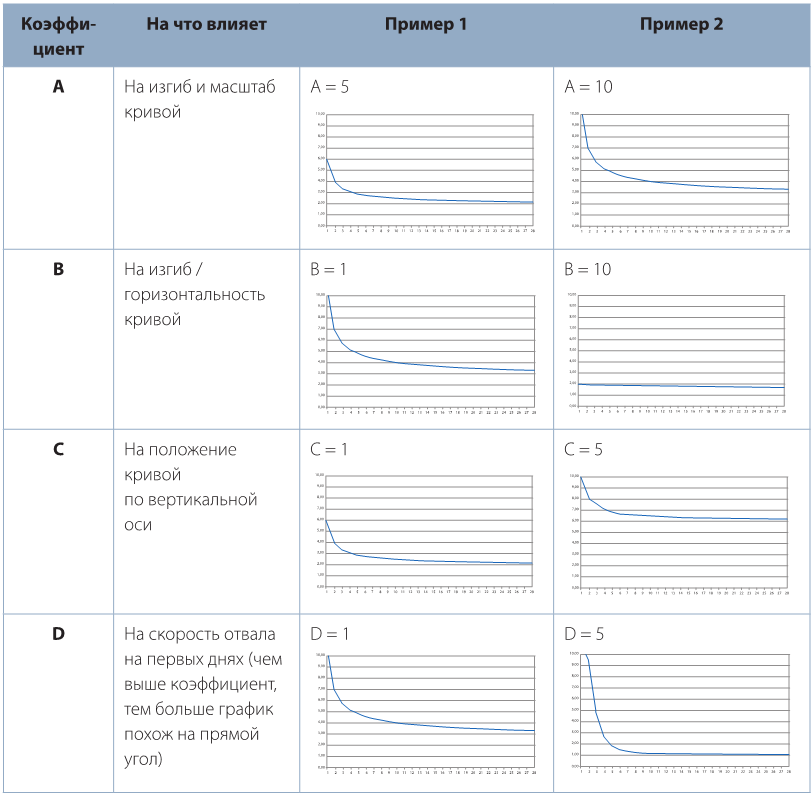
Вывод:

для аппроксимации Retention хорошо подходят три вида кривых:

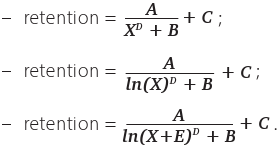
Победителей мы огласили, теперь хотим отметить несколько важных моментов, которые нужно иметь в виду при аппроксимации Retention.

1. Если у вас мало исходных точек, то лучше использовать ту кривую, в которой меньше коэффициентов. И запомните: никогда не используйте кривую, у которой неизвестных коэффициентов больше, чем точек! Скажем, если у вас есть лишь три точки Retention (допустим, 1 дня, 7 дня, 28 дня), то максимальное количество коэффицентов, которые вы можете использовать, – это три, и в этом случае лучше всего подойдет функция .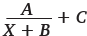

2. Вы всегда вольны менять оптимизационную функцию как вздумается (мы воспользовались стандартным МНК и применили простую сумму квадратов отклонений). Допустим, вам не так важно поведение Retention в другие периоды, но вы хотите, чтобы модельное и фактические значения Retention точь-в-точь совпали на 180 днях. Поэтому для оптимизационной функции отклонение на 180 днях можно взять с большим коэффициентом или в большой степени.

3. Мы даем вам не универсальную рекомендацию, а просто наш опыт решения нескольких разовых задач. Не исключено, что есть и другие функции, более точно аппроксимирующие показатели удержания. Но функции, которые мы использовали, дали хороший результат. Они сложны и, вероятно, для некоторых задач подойдут и более простые функции типа того же логарифма. Но для моих задач эти сложные функции сработали отлично.