Один необычный тип дуальности носит название струнно-калибровочной дуальности. Необычность этой дуальности заключается в том, что она устанавливает не соответствие теории струн типа IIB и другой теории струн, а соответствие теории типа IIB и калибровочной теории. В пятой главе я рассказывал о калибровочной симметрии. Позвольте напомнить её основные моменты. Калибровочная симметрия гарантирует безмассовость фотона. Ещё она гарантирует, что направление спина фотона совпадает с направлением его движения. И она позволяет нам рассматривать электрический заряд как вращение в некотором абстрактном пространстве. Калибровочная теория — это теория, математическое описание которой включает калибровочную симметрию. Обычно это означает, что такая теория содержит фотоны или объекты, похожие на фотоны. Простейшим примером калибровочной теории является теория электромагнетизма. Более сложные калибровочные теории есть не только у струнных теоретиков, но и у ядерных физиков, и у физиков, изучающих элементарные частицы, и у исследователей конденсированных сред.

Вы, возможно, помните, что калибровочная симметрия фотонов и электронов таинственным образом совпадает с круговой симметрией. Заряженный объект, такой как электрон, обладает эффективным вращением по абстрактной окружности. Не следует воспринимать эту окружность буквально, как, например, одиннадцатое измерение в M-теории. Это всего лишь математическая абстракция, помогающая описать электрический заряд электрона и его взаимодействие с фотонами. Одним из аспектов этой математики является то, что фотоны сами не несут электрический заряд, но могут его «чувствовать».

Естественно задаться вопросом: если с фотонами ассоциирована круговая симметрия, то нет ли калибровочной теории, с которой была бы ассоциирована сферическая симметрия? Есть такая теория! Она содержит три вида фотонов, соответствующих трём возможным осям, вокруг которых можно повернуть сферу (в авиации эти три независимых направления вращения носят названия крен, тангаж и рысканье). В отличие от обычных фотонов, фотоны в этой теории заряжены. Помните, мы говорили об облаке виртуальных частиц, окружающем электроны или гравитоны? Напомню основные положения. Существует чёткое различие между гравитацией, где гравитоны могут непосредственно порождать другие гравитоны, и электромагнетизмом, где фотоны могут рождать другие фотоны только через рождение пар заряженных частиц или при рассеянии на заряженных частицах. В последнем случае мы можем просчитать все процессы рождения виртуальных частиц со сколь угодно высокой точностью. Про такую теорию говорят, что она перенормируема. Эта теория называется квантовой электродинамикой, или сокращённо КЭД. Теория гравитации, напротив, неперенормируема. Это означает, что у нас нет математического аппарата, способного полностью и до конца описать весь процесс каскадного рождения гравитонов. А что с калибровочной теорией, ассоциированной со сферической симметрией? Оказывается, она больше похожа на КЭД, чем на теорию гравитации, то есть она перенормируема.

Краеугольным камнем для понимания физических процессов, происходящих внутри протона, является калибровочная теория, называемая квантовой хромодинамикой, или сокращённо КХД. Она основывается на группе симметрии, содержащей восемь различных типов вращения. Как вы уже догадались, эти вращения происходят не в обычных четырёх измерениях. Они происходят в особом абстрактном математическом пространстве, называемом цветовым пространством. КХД очень похожа на калибровочную теорию, ассоциированную со сферической симметрией, только она более сложная, из-за того что оперирует восемью типами поворотов в отличие от трёх: крена, тангажа и рысканья, присущих трёхмерной сферической симметрии. Каждый из восьми типов вращения соответствует частице, похожей на фотон. Эти восемь частиц называются глюонами. Кроме них существуют частицы, похожие на электроны, называемые кварками, но если электрон имеет только отрицательный электрический заряд, то кварки могут обладать тремя разными типами зарядов. Эти заряды называются цветами, а цветовое пространство служит математическим инструментом, позволяющим работать с цветовыми зарядами. Заряд кварка может быть красным, зелёным и синим, но это всего-навсего фигура речи: указанные цвета не имеют никакого отношения к цветам, которые различает человеческий глаз. Глюоны также несут цветовые заряды и «чувствуют» друг друга подобно гравитонам. Но, в отличие от неконтролируемого размножения гравитонов, каскадное рождение виртуальных частиц кварками поддаётся математическому описанию. Таким образом, КХД, как и КЭД, тоже является перенормируемой теорией. Её название было выбрано не случайно: она очень сильно напоминает квантовую электродинамику, а слово «хромодинамика» дословно означает «движение цветов», только понятие «цвет» в квантовой хромодинамике не имеет отношения к обычным цветам, а всего лишь служит удобной визуализацией математической абстракции.

Кварки, глюоны и цвета-которые-не-цвета придают КХД такое же причудливое звучание, как и теории струн, но, в отличие от теории струн, КХД очень хорошо проверена экспериментально и единодушно признаётся корректным описанием физики внутри протона. КХД имеет много необычных особенностей, наиболее важная из которых заключается в том, что мы не можем наблюдать голый кварк: он всегда одет в «шубу» из глюонов и связан с другими кварками. Протоны и нейтроны представляют собой подобные связанные состояния кварков, а вот электроны — нет. Похоже, что электроны вообще не имеют ничего общего с кварками. Или более строго: они присутствуют в теоретической физике на равных правах с кварками. Одна из непроверенных гипотез в современной физике утверждает, что электрический заряд может оказаться четвёртым цветовым зарядом. Эту гипотезу мы обсудим в седьмой главе.

Колебания D3-бран описываются калибровочной теорией, похожей на КХД. Ранее мы уже говорили о колебаниях D1-бран. Вкратце: колебания D1-браны можно представить двумя способами: либо как рябь, бегущую по бране, либо как струну, прикреплённую к бране и скользящую по ней. Второй способ описания лучше, чем первый, обобщается на случай D3-бран. Возьмём три D3-браны и расположим их одна над другой, для удобства присвоив им цветовые обозначения. Одну брану назовём красной, другую — синей, а третью — зелёной. Если струна прикреплена одним концом к красной бране, а другим — к синей, какого она будет цвета? Интуитивно кажется, что пурпурного. Ну нет, подобная цветовая метафора уведёт нас слишком далеко. Правильнее будет сказать, что цвет струны плавно перетекает из красного в синий. Оказывается, именно такими цветами обладают глюоны. Теперь понятно, откуда берутся восемь типов глюонов. Три глюона имеют цвета: красно-красный, красно-синий и красно-зелёный, ещё три начинаются с зелёного цвета, и ещё три — с синего. Итого — девять. Упс! Перебор. К сожалению, для объяснения, почему в действительности глюонов не девять, а восемь, мне пришлось бы задействовать слишком сложный математический аппарат.

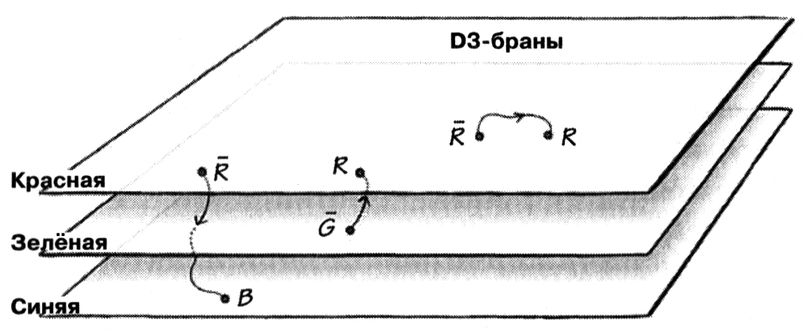
Три D3-браны, расположенные одна над другой, обозначены как «красная», «зелёная» и «синяя». Струны, идущие от одной браны к другой, используются для описания колебаний бран

Если не брать во внимание небольшую проблему с лишним глюоном, то примерно понятно, как можно получить глюоны из трёх D3-бран, соединённых струнами. С кварками несколько сложнее. Я опущу этот вопрос, чтобы показать главную изюминку: я взял три D3-браны, соединил их струнами и получил глюоны. Если бы я взял одну D3-брану, я бы получил фотоны. Взяв две D3-браны, я получу уже упоминавшуюся ранее калибровочную теорию, ассоциированную со сферической симметрией. В общем случае, взяв N бран, я получу теорию, содержащую порядка N² глюонов.

Теперь вспомним, что если взять много бран и сложить их вместе, то такая конструкция лучше всего описывается чёрной дырой с нулевой температурой. В пятой главе я показал это на примере D0-бран. С D3-бранами получится то же самое. Сложенные одна над другой, они искривят пространство-время вокруг себя, и в их непосредственной окрестности возникнет горизонт чёрной дыры. Из-за большого количества измерений наглядно изобразить форму окружающего D3-браны горизонта очень трудно. Представьте себе нечто, напоминающее цилиндр, двумерная поверхность которого круглая в пяти измерениях и прямая ещё в трёх. Всего восемь измерений. Представили? Кажется, что всё это достаточно далеко от КХД. При наличии у D3-бран дополнительной колебательной энергии горизонт немного увеличивается в размерах и приобретает ненулевую температуру.

Важнейшей деталью струнно-калибровочной дуальности является возможность применить к колебаниям D3-бран формулу E = k_BT и получить представление о температуре горизонта, окружающего D3-браны. Позвольте мне попытаться объяснить, почему это считается струнным дуализмом. Существует два способа описания D3-бран ненулевой температуры. Один состоит в том, чтобы учесть все открытые струны, скользящие по D3-бранам, другой — в том, чтобы следить за окружающим D3-браны горизонтом. Эти два представления являются взаимодополняющими в следующем смысле. Если у вас есть горизонт, то вы не можете сказать наверняка, что находится внутри него. Другими словами, существование горизонта не позволяет следить за струнами на D3-бранах. По крайней мере вы не можете отслеживать поведение каждой из них по отдельности. Всё, что вы можете, — это отслеживать какие-то коллективные свойства струн, такие как их суммарная энергия. Наличие горизонта означает, что глюоны взаимодействуют сильно. Они часто расщепляются и соединяются. Они то появляются, то исчезают. Они одеваются в сложные каскадные конструкции из других глюонов. Как и в случае сильновзаимодействующих струн, когда струны перестают быть похожи на струны, так и сильновзаимодействующие глюоны перестают быть похожи на глюоны. Появление горизонта — это что-то вроде раскрытия дополнительных измерений в M-теории. Для объяснения динамики сильновзаимодействующих глюонов нужен язык, который требует дополнительных измерений.

Применение струнно-калибровочной дуальности не ограничивается слежением за энергией тепловых глюонов. Главным является именно эквивалентность калибровочной теории глюонов на D3-бранах и геометрии чёрной дыры вокруг D3-бран. Это утверждение может показаться странным, потому что криволинейная геометрия является 10-мерной, тогда как глюоны «знают» только о четырёх измерениях. Ещё более странным выглядит то, что эта дуальность устанавливает соответствие между теорией с гравитацией (теория струн в окрестности D3-бран) и теорией без гравитации (калибровочная теория на D3-бранах). На первый взгляд она кажется более узкой дуальностью, чем другие. T-дуальность, например, устанавливает полное соответствие между теорией типа IIB и теорией типа IIA. Она содержит правила для отображения любого типа D-бран на любой другой тип. А струнно-калибровочная дуальность выглядит как ограниченная только одним типом бран — D3-бранами. На самом деле другие типы бран входят в струнно-калибровочную дуальность достаточно интересным образом, например, приводя к существованию кварков наряду с глюонами. Я ещё вернусь к струнно-калибровочной дуальности в главе 8, где расскажу о попытках «пристегнуть» её для описания столкновений тяжёлых ионов.

В заключение я хочу отметить, что, с одной стороны, дуальности теории струн отличаются от симметрий, а с другой — может показаться, что это одно и то же. Два описания, связанные отношением дуальности, могут требовать пространств разной размерности или, как вы только что видели, одно может содержать гравитацию, а другое — нет. Это не похоже на симметрию такого объекта, как квадрат. У квадрата есть четыре одинаковых угла, и можно описать набор преобразований, отображающий квадрат на себя. С другой стороны, существуют некоторые струнные дуальности, в которых две стороны явления выглядят как зеркальные отражения друг друга. Например, теории типа IIA и IIB очень похожи, за исключением различия в типах бран, существование которых они допускают. Струнные дуальности устанавливают соответствие разных теорий струн с низкоэнергетической супергравитацией способом, который тесно связан с обычной симметрией, такой как симметрия квадрата. Вполне возможно, что мы не до конца понимаем струнные дуальности, потому что большая часть того, что мы понимаем, ограничена низкоэнергетическими теориями.