Я представил D-браны в качестве места в пространстве-времени, где закреплены концы струны, но, оказывается, есть ещё один способ представления D-бран: в качестве чёрных дыр с нулевой температурой. Лучше всего это представление работает для случая большого количества бран, расположенных одна над другой. Начнём с D0-бран. Как я только что объяснил, в теории суперструн две D0-браны не оказывают силового воздействия друг на друга. Их гравитационное притяжение компенсируется электростатическим отталкиванием, и они не аннигилируют друг с другом подобно D0-бранам и анти-D0-бранам. Так что мы можем рассматривать две D0-браны рядом друг с другом или вообще любое количество D0-бран, не беспокоясь о таких неприятностях, как аннигиляция. Но чем больше D0-бран мы собираем в наш клубок, тем сильнее искривляется пространство вокруг них, принимая в пределе форму горизонта чёрной дыры. Для пущего правдоподобия возьмём миллион D0-бран, помещённых рядом друг с другом, и одну D0-брану, движущуюся рядом. Одинокая D0-брана не испытывает на себе ни притяжения, ни отталкивания. Впрочем, это не совсем так. На самом деле одинокая D0-брана не испытывает никакой силы, если она не движется. Если же она движется, то она испытывает небольшую силу, тянущую её, как буксир, к другим бранам. Подобная сила удерживает наш клубок из миллиона бран от рассыпания. Для анти-D0-браны всё обстоит совершенно по-другому. Она испытывает как гравитационное, так и электростатическое притяжение, и, оказавшись достаточно близко от нашего миллионнобранного клубка, уподобляется одной из тех рыб, что подплыли слишком близко к стоку из озера, — её засасывает в него, и никакой физический процесс не может остановить её после того, как она подошла ближе определённой дистанции. Это, так сказать, «на пальцах», и есть понятие горизонта чёрной дыры.

А почему горизонт имеет нулевую температуру? Это объяснить труднее. Всё дело в поведении одинокой D0-браны, которая не испытывает на себе результирующей силы со стороны нашего клубка. Оказывается, что факт отсутствия такой силы глубоко связан с нулевой температурой. Оба этих свойства вытекают из требований суперсимметрии. Я отложу подробное обсуждение суперсимметрии до главы 7, а сейчас добавлю к тому, что мы постепенно узнаем о суперсимметрии, два утверждения. Первое: суперсимметрия относится к гравитонам и фотонам. Гравитоны ответственны за гравитационное притяжение. Фотоны ответственны за электростатическое притяжение или отталкивание. Частное соотношение, предполагаемое суперсимметрией между гравитонами и фотонами, утверждает, что гравитационные и электростатические силы одинаковы. Второе: суперсимметрия гарантирует стабильность D0-бран. Это означает, что в теории струн не существует объекта легче D0-браны и, соответственно, D0-брана не может ни во что превратиться, если только не встретится с анти-D0-браной. И хотя D0-брана и кажется достаточно тяжёлой, она в корне отличается от тяжёлого ядра урана-235, которое может распадаться на более лёгкие ядра криптона и бария, в то время как бране распадаться не на что.

Клубки из D0-бран также стабильны. Они не могут распадаться на что-нибудь ещё. Единственное, что они могут, — это слегка вибрировать. Это точно такие же колебания, как и тепловые колебания атомов в куске угля. Как вы помните, энергия тепловых колебаний описывается формулой E = k_BT. Здесь E представляет собой дополнительную энергию тепловых колебаний. Например, когда вы применяете эту формулу к атому углерода в куске антрацита, то E является дополнительной энергией тепловых колебаний атома, но не его энергией покоя. Общая же энергия куска угля должна включать в себя энергию покоя всех атомов плюс энергию их тепловых колебаний. Атомы также испытывают квантовые флуктуации относительно своих средних положений, и, в принципе, энергия нулевых колебаний тоже входит в общую энергию. Это всё очень напоминает наши предыдущие обсуждения о трёх вкладах в массу струны. Полная масса куска угля может быть получена из его полной энергии при помощи формулы E = mc².

А теперь перенесём всё сказанное о куске угля на наш клубок из D0-бран. У них есть масса покоя и масса, соответствующая энергии нулевых колебаний. В случае D0-бран вклад энергии нулевых колебаний в полную массу в точности равен нулю. Отслеживание вклада этих квантовых флуктуаций доставляет постоянную головную боль теоретикам. Но D0-браны обязаны обладать хоть какой-то энергией тепловых колебаний. Если так, то клубок из D0-бран должен иметь некоторую температуру и соответствующую ей дополнительную массу. Но дополнительный заряд клубку эта добавка не приносит. Следовательно, если одинокая D0-брана оказывается поблизости от клубка с ненулевой температурой, она будет испытывать дополнительное гравитационное притяжение, но не будет испытывать дополнительного электростатического отталкивания и суммарная сила, действующая на неё, не будет равна нулю. Если же мы охладим клубок до абсолютного нуля, то термальная добавка к его массе исчезнет и вместе с ней исчезнет и дополнительная гравитационная сила притяжения. Таким образом, отсутствие дополнительной силы притяжения, действующей на D0-брану, приводит нас к требованию нулевой температуры клубка.

Если все эти разговоры о D0-бранах сбили вас с толку, давайте снова вернёмся к куску угля. Его тепловые колебания дают вклад в его полную энергию, так же как и у клубка D0-бран. Эта полная энергия по-прежнему является энергией покоя куска угля. «Покой» в данном случае означает, что кусок угля лежит неподвижно на столе, а не летит, со свистом рассекая воздух. Полная энергия покоя связана с полной массой формулой E = mc². Значит, нагретый кусок угля в действительности тяжелее, чем холодный, и точно так же горячий клубок D0-бран тяжелее холодного. Мы можем подсчитать, какую добавку к массе получает кусок угля при нагревании. Очень горячий уголь имеет температуру около 2000 кельвинов. Солнечная фотосфера, как вы помните, в три раза горячее. Формула E = k_BT даёт оценку энергии одного атома — но только оценку. Используя эту довольно грубую оценку, я получил, что нагревание угля до 2000 кельвинов увеличивает его массу покоя примерно на 10⁻¹¹ от первоначальной величины. Это одна стомиллиардная. Тем не менее это существенно больше, чем относительное увеличение массы спринтера на стометровке за счёт его кинетической энергии. Но это во много-много раз меньше, чем доля массы покоя, высвобождающаяся при ядерных реакциях распада. Вот, кстати, почему атомные электростанции считаются перспективнее угольных. Одна тонна урана, загруженная в современный ядерный реактор, способна произвести столько же электроэнергии, сколько сто тысяч тонн угля.

Сомневаюсь, что вы обрадуетесь, узнав, что при описании D0-бран я использовал два упрощения. Во-первых, я утаил от вас, что D0-браны взаимодействуют друг с другом ещё одним способом и переносчиком этого взаимодействия являются безмассовые частицы, отличные от фотонов и гравитонов. Эти частицы называются дилатонами, и они обладают нулевым спином. Всё, что ранее было сказано о гравитационном взаимодействии, должно быть расширено с учётом дилатонов. Однако даже с учётом этой небольшой добавки к гравитации все основные выводы остаются прежними. Во-вторых, D0-браны обладают горизонтом, поэтому трудно сказать, вибрируют ли они, подобно атомам. Всё, что мы можем сказать, и всё, в чём мы можем быть уверены, — это в том, что клубок D0-бран имеет дополнительную энергию и, как следствие, дополнительную массу. Более точное описание чёрных дыр, образованных вибрирующими D0-бранами, представляет в теории струн большую проблему. Лучше всего исследованы случаи D1-бран и D5-бран. Важным случаем являются D3-браны, которые исследованы несколько хуже, а вот с количественным описанием D0-бран всё грустно, несмотря на то что в последнее время в этой области достигнут значительный прогресс.

Главное, что меняется при переходе от изучения чёрных дыр, образованных D0-бранами, к чёрным дырам, образованным D1-бранами или D3-бранами, — это форма горизонта. Горизонт D3-бран очень трудно представить наглядно, потому что D3-брана простирается за пределы привычных трёх пространственных измерений. Более или менее наглядно можно представить себе только одно дополнительное измерение, чтобы получить правильное представление о том, как может выглядеть горизонт в многомерном пространстве. Это чрезвычайно интересное занятие, и в последующих главах я постараюсь всё объяснить, а сейчас попытаемся рассмотреть D1-брану в привычном четырёхмерном пространстве-времени, предположив, как мы уже ранее это делали, что нам каким-то образом удалось избавиться от лишних шести измерений. D1-брана вытянута вдоль прямой, выглядит как флагшток, а её квантовые флуктуации напоминают рябь на этом флагштоке, но если мы расположим рядом друг с другом много D1-бран, то количество различных типов ряби, или мод колебаний, существенно возрастёт. Удобнее всего представить эти моды в виде струн. Я не оговорился, сейчас объясню. Струна может быть закреплена одним концом на одной D1-бране, а вторым — на другой, при этом концы струн могут скользить по D1-бранам. Струны, имеющие концы, называются открытыми струнами в противоположность закрытым струнам, замкнутым в кольцо. Наличие у D1-бран тепловых колебаний эквивалентно наличию прикреплённых к ним струн, и, как оказалось, открытые струны описывают все возможные типы малых колебаний D1-бран. Другими словами, струны и есть та самая рябь на D1-бранах.

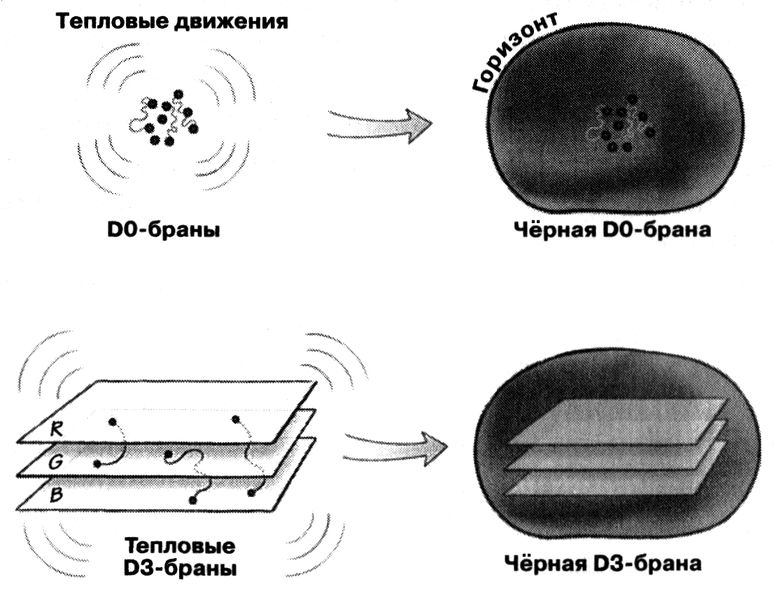
Слева вверху: клубок из D0-бран обладает тепловой энергией. Справа вверху: форма горизонта вокруг D0-браны, описывающая её тепловые свойства. Слева внизу: три D3-браны одна над другой. Струны между бранами ведут себя подобно глюонам и обеспечивают тепловую энергию. Справа внизу: форма горизонта вокруг D3-бран, описывающая их тепловые свойства

Если взять много D1-бран, то они вместе с прикреплёнными к ним открытыми струнами искривят пространство-время вокруг себя, что приведёт к возникновению горизонта, имеющего круговую симметрию, поскольку D1-браны имеют протяжённость в одном измерении. Этот горизонт можно представлять в виде цилиндра, окружающего пучок D1-бран, и, как вы видите, его форма отличается от сферически симметричного горизонта клубка D0-бран. Некоторые из струнных теоретиков предпочитают при описании группы D1-бран, окружённой горизонтом, использовать термин чёрная брана, чтобы отличать данный случай от чёрной дыры, образованной клубком D0-бран и имеющей сферический горизонт. Я предпочитаю не заморачиваться с терминологией и каждый раз объяснять, что я имею в виду под чёрной браной или чёрной дырой, а всегда конкретно указывать на тип геометрии горизонта, используя термины чёрная D0-брана, чёрная D1-брана и так далее.

Интересно, что исторически геометрия, описывающая чёрную дыру (или чёрную брану), образованную клубком D-бран, была известна задолго до того, как теоретики поняли, что такое D-браны. Всё, что нужно для описания чёрной браны, — это решить уравнения супергравитации, которая, как вы, возможно, помните, является низкоэнергетическим пределом теории суперструн, когда мы пренебрегаем всеми обертонами колебаний струн, за исключением безмассовых. Супергравитация всё ещё весьма сложная теория, но она куда проще полной теории суперструн. Конструирование чёрных бран было одним из стимулов, которым супергравитация толкала развитие теории струн во время второй суперструнной революции.