Я потратил много времени на рассказ о колебаниях и флуктуациях струн в пространстве-времени. Но давайте вернёмся на шаг назад и спросим себя: «А что такое пространство? И что такое время?».

Существует точка зрения, согласно которой пространство является производной сущностью и имеет смысл только в отношении присутствующих в нём объектов. С этой точки зрения пространство описывается в терминах расстояний между объектами. Аналогично, время также не имеет смысла само по себе, а существует только как описание последовательности событий. Рассмотрим пару частиц A и B. Принято считать, что каждая из них движется по некоторой траектории в пространстве-времени и, если траектории частиц пересекаются, частицы сталкиваются. На первый взгляд в такой парадигме нет ничего плохого, но посмотрим с другой точки зрения. Что, если пространство и время не имеют никакого смысла в отсутствие частиц? Что это могло бы значить? Описывая траекторию частицы A, мы могли бы задать набор её пространственных координат как функцию времени и то же самое — для частицы B. Сделав это, мы можем свести роль пространства исключительно к механизму задания зависимости координат частиц от времени. Также мы будем знать, что частицы столкнулись, если пространственные и временны́е координаты частиц совпали.

Если это звучит для вас слишком абстрактно, представьте себе на месте частиц гоночные автомобили, снабжённые GPS-навигаторами и часами. Что мы можем узнать, изучая записанные GPS-навигаторами треки? Предположим, оба автомобиля движутся по одной и той же трассе, и первое, на что мы обращаем внимание, — автомобили периодически возвращаются в одну и ту же точку, пройдя одну и ту же дистанцию — длину гоночной трассы. Самые проницательные из нас воскликнут: «Ага! Трасса замкнута в кольцо». Допустим далее, мы обнаруживаем, что автомобили часто меняют свою скорость. Поломав голову, мы выскажем предположение, что автодром представляет собой не идеальный круг, а имеет повороты, на которых автомобили тормозят, и прямые участки, где автомобили разгоняются. А ещё мы бы могли заметить, что все автомобили, записи с которых у нас имеются, движутся по трассе в одном и том же направлении. Это привело бы нас к гипотезе о том, что существует некое правило, согласно которому все объекты, находящиеся на трассе, должны двигаться по ней в одном направлении. Наконец, мы бы обратили внимание на то, что автомобили часто сближаются друг с другом, но очень редко сталкиваются, и это навело бы нас на мысль, что столкновения автомобилей не являются главной целью автогонки.

Получается, что, только изучая GPS-треки гоночных автомобилей и применяя дедуктивный метод, вы можете кое-что узнать о геометрии автодрома и правилах гонок. Может показаться, что мы делаем это через... понятно что, вместо того чтобы просто посмотреть гонку вживую. Однако на самом деле наблюдение живой гонки — очень сложный процесс. Вы стоите у края гоночного полотна, и это означает, что вы не присутствуете одновременно во всех точках трассы. Вы смотрите на автомобили, и это означает, что вы видите не сами автомобили, а фиксируете отражённые от них фотоны, что заставляет принимать во внимание множество других физических явлений. Гораздо проще анализировать треки GPS, содержащие всю необходимую информацию о местоположении автомобилей в каждый момент времени. С GPS-треками вам не приходится вникать в такие тонкости, как положение зрителей на трибунах или отражение и преломление снующих туда-сюда фотонов. Вам не нужно спрашивать, да вы на самом деле и не можете задать осмысленный вопрос, существует ли мир за пределами автодрома. Вы даже не нуждаетесь в предположении о существовании самого автодрома. Вместо этого вы можете логически вывести его существование и предположить некоторые из его свойств, изучая записи движения автомобилей.

Многое в теории струн происходит похожим образом. На основании характера движения и взаимодействия струн делаются предположения о свойствах пространства-времени. Такой подход называется теорией струн на мировом листе. Мировой лист — это способ представления движения струн. GPS-трек движения автомобиля представляет собой мировую линию в пространстве-времени. Со струнами всё оказывается сложнее по двум причинам. Во-первых, струны — не точки. Они имеют протяжённость, поэтому, чтобы задать положение струны, вы должны задать положение всех её точек. Во-вторых, струны существуют в 26-мерном или, в лучшем случае, в 10-мерном пространстве, и эти пространственные координаты могут быть искривлены или свёрнуты довольно сложным образом. В отличие от зрителя автогонки, физик не может встать в сторонке и взглянуть оттуда на геометрию пространства-времени. Осмысленные вопросы имеют отношение только к характеру движения и взаимодействия струн. Само же пространство-время в теории струн на мировом листе имеет смысл лишь в аспекте поведения струн, но не само по себе.

Мировой лист струны является поверхностью. Если мы проведём по этой поверхности разрез, то получим кривую, которая и представляет собой струну. Разрезая лист разными способами, мы получим набор кривых; этот набор является аналогом набора точек, из которых состоит GPS-трек автомобиля. Каждая точка GPS-трека представляет положение автомобиля в определённый момент времени; аналогично каждая кривая, вырезанная из мирового листа, представляет струну в определённый момент времени.

Чтобы описать движение струны в пространстве-времени, необходимо для каждого момента указать положение в пространстве каждой точки на мировом листе. Представьте себе, что мы приклеили на мировой лист множество ярлычков. Вырезая из мирового листа кривую, вы получаете цепочку ярлычков, на каждом из которых записаны координаты и время. Мировой лист в целом представляет собой поверхность, которую заметает струна при своём движении в пространстве-времени.

Чтобы лучше понять, что я имею в виду под маркировкой мирового листа ярлычками, представьте себе топографическую карту. На ней проведены горизонтали, или линии равных высот. Каждая из этих линий помечена ярлыком, обозначающим высоту. Если линии идут слишком часто, то метки ставятся только у некоторых из них, например у каждой пятой. Топографическая карта является плоским листом, но она отображает трёхмерный рельеф местности.

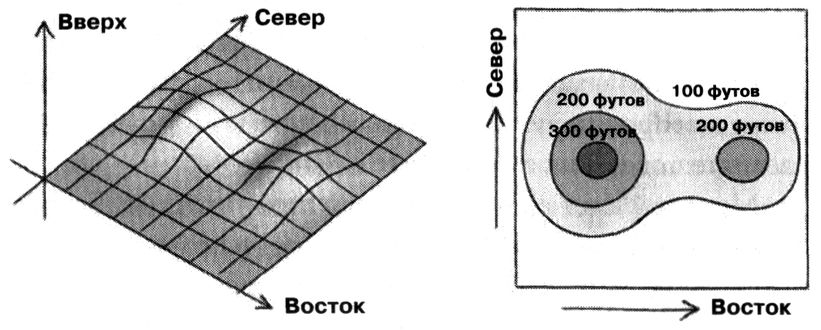
Слева: два холма, разделённые седловиной. Справа: топографическая карта холмов с горизонталями, обозначающими линии равных высот

Хорошей аналогией является представление мирового листа струны как топографической карты, горизонтали которой описывают различные положения струны в пространстве-времени. Но можно встать на другую точку зрения и сказать, что мировой лист струны — это всё, что у нас есть, а пространство-время — не более чем набор ярлычков. На обычных топографических картах отметки горизонталей — это высоты над уровнем моря, и весь набор ярлычков — это просто набор возможных высот точек земной поверхности: от −400 до +8800 метров, исключая океаническое дно. На мировом листе теории струн каждый ярлычок — это положение в 26-мерном пространстве (или в 10-мерном в случае суперструнной теории). Некоторые из этих 26 измерений могут быть свёрнуты в кольцо и замкнуты сами на себя, как кольцевая гоночная трасса. Основная идея нашей концепции состоит в том, что пространство время «возникает» из способа, которым вы маркируете мировой лист, как если бы высота зависела от того, что вы нарисуете на топографической карте.

Подведём промежуточные итоги, а затем перейдём к одной из главных изюминок теории струн на мировом листе. Обычно мы представляем струны вибрирующими в пространстве-времени. Но пространство и время не обязаны быть абсолютными понятиями. Даже лучше, если это не так, потому что тогда некий внешний динамический принцип мог бы управлять формой пространства-времени. Именно так и случилось в теории струн. В теории струн на мировом листе пространство-время является просто набором ярлыков, позволяющих описать движение струны. Квантовая механика требует, чтобы эти ярлыки немного колебались. А теперь: барабанная дробь! В конечном итоге выходит так, что вы можете отслеживать эти квантовые флуктуации, только если пространство-время подчиняется уравнениям общей теории относительности. Общая теория относительности — напомню — это современная теория гравитации. Итак, квантовая механика плюс теория струн на мировом листе включают в себя гравитацию. Круто!

Объяснения «отслеживания» квантовых флуктуаций пространственно-временных ярлыков на мировом листе уведут нас глубоко в технические дебри, но я могу попытаться объяснить это «на пальцах», используя аналогию с гоночной трассой. Помните, я предположил, что мы могли бы догадаться, что автодром состоит из поворотов и прямых участков, заметив, что автомобили тормозят в одних местах трассы и разгоняются в других? Автодром также не имеет острых углов, потому что, чтобы повернуть в таком месте, автомобиль должен почти остановиться, что противоречило бы духу автогонок. В общей теории относительности тоже почти нет острых углов в пространстве-времени, потому что уравнения ОТО их запрещают. Я говорю «почти», потому что на самом деле острые углы, или, как их называют теоретики, сингулярности, разрешены, но только за горизонтом чёрных дыр. Интуитивно можно понять отсутствие острых углов в пространстве-времени по аналогии с отсутствием их на автодроме. Струны не могут проходить через сингулярности, так же как гоночные автомобили не могут проходить острые углы трассы без остановки, хотя есть и исключения. Исследование разрешённых типов сингулярности представляет собой отдельный и крайне увлекательный раздел теории струн. Обычно эти сингулярности не могут быть поняты в рамках общей теории относительности, так что теория струн разрешает существование гораздо более богатых классов геометрии пространства-времени, чем теория относительности.

Дополнительные геометрии возникают в теории струн в некоторых случаях, связанных с бранами, о которых пойдёт речь в следующей главе.