Книга: Космос. Иллюстрированная история астрономии и космологии
Назад: АСТРОНОМЫ-ПРАКТИКИ
Дальше: ЧАСЫ И МИРОЗДАНИЕ
РИЧАРД УОЛЛИНГФОРДСКИЙ
Оксфордский университет обладал долгой научной традицией, особенно в преподавании аристотелевской натуральной философии, и в течение XIII в. оксфордская астрономия уделяла внимание главным образом производству несложных обучающих трактатов о сфере и календаре, а также о космологических вопросах, вытекавших из произведения Аристотеля «О небе». Затем вошедшие в употребление Толедские таблицы и каноны к ним помогли консолидировать астрономическое обучение и отрегулировать терминологию, но вплоть до начала XIV в. там не появилось ничего более или менее оригинального. Серия таблиц, составленная в 1310–1316 гг. астрономом из Мертон-колледжа Джоном Маудитом, привлекла внимание многих ученых к тригонометрии, положенной в основу сферической астрономии, и стала предметом первых штудий в этой области для одного из наиболее выдающихся астрономов Средних веков Ричарда Уоллингфордского (ок. 1292–1336).
Традиционно, астрономов раннего периода ранжируют в соответствии с оригинальностью, которую они демонстрировали при разработке новых планетных систем, однако при таком подходе мы упускаем из виду казавшееся в XIV в. наиболее насущным, а именно – методы быстрого счета и представления данных. В своем стремлении разработать их Ричард Уоллигфордский выдвинул множество оригинальных идей, продемонстрировавших незаурядную изобретательность ума и вызвавших значительный (хотя не всегда явно признаваемый) резонанс. Он был монахом-бенедиктинцем, окончил Оксфорд и преподавал там до 1327 г. В этом году он вернулся в свой монастырь в Сент-Олбанс – элитный монастырь старой Англии, – чтобы занять там должность аббата. Посетив Авиньон (место, где в то время находился папский престол) для получения санкции папы на утверждение в новой должности, он вернулся обратно в Англию, где неожиданно обнаружил, что болен проказой. Монахи отнюдь не избегали Ричарда, они гордились его достижениями и даже позволили ему оставаться аббатом вплоть до смерти.
Сочинение Ричарда Уоллингфордского «Quadripartitum» – это первый обстоятельный трактат по сферической тригонометрии, написанный в христианской Европе. Разрабатываемые в нем идеи основывались на «Альмагесте», толедских канонах и небольшом трактате, написанном, предположительно, Джованни Кампано. Будучи аббатом, он нашел время для его переработки с учетом труда севильского астронома XII в. Джабира ибн Афлаха – одного из двух ученых, известных на Западе под именем Гебер; второй более известен как алхимик. Перед тем как покинуть Оксфорд, Ричард написал еще три работы и несколько более легких сочинений. Его трактат «Exafrenon» посвящен астрологической метеорологии и являлся хотя и стройно написанным, но не оригинальным сочинением. Кроме того, он написал работу об инструменте собственной конструкции под названием «ректангулус». Третья работа посвящена его экваториуму, который он называл «альбион».
В «Quadripartitum» дано точное решение задач из области геометрии сферы, включая, например, сферические треугольники, но приводимые расчеты оказались чрезвычайно трудными и запутанными. Армиллярная сфера позволяла получить приближенные решения, но крайне трудно изготовить ее со всей требуемой точностью. Хотя торкветум, изобретенный, предположительно, в XIII в. Франко Польским, на первый взгляд, сильно отличался от армиллярной сферы, он имел с ней много общего. (На ил. 103 приведен один из образцов этого инструмента, датируемый XVI в.) Геометрическая проблема, с которой сталкивались все серьезно работающие астрономы, заключалась в разложении векторов по трем измерениям. С точки зрения механики проблема заключалась в том, чтобы добиться одновременного вращения визирной линейки вокруг трех различных осей, особенно тех, которые расположены под прямым углом к экватору и эклиптике. (Здесь уместно будет вспомнить гениальную конструкцию кубика Рубика или его сферического аналога.) Принимая во внимание огромные расстояния до наблюдаемых небесных объектов, астрономам не обязательно было совмещать все оси в одном центре. С помощью своего ректангулуса Ричард Уоллингфордский продвинул на шаг вперед упрощения, достигнутые в торкветуме. Его новый инструмент включал в себя систему из семи прямых линеек, а круговые шкалы в нем отсутствовали (ил. 104). Он не мог вращать эти семь линеек в различных плоскостях вокруг одной и той же точки, однако он изобрел систему смещенных шарниров, и этого оказалось вполне достаточно. В принципе, ректангулус годился для проведения наблюдений и более или менее непосредственного определения координат. Прямые линейки ректангулуса можно было изготовить и проградуировать с максимально доступной точностью. Несмотря на некоторые недостатки, саму конструкцию ректангулуса можно считать воплощением выдающейся изобретательской интуиции.
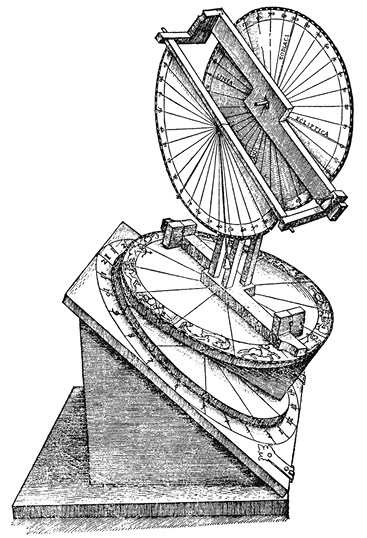
103
Торкветум из сочинения Петера Апиана «Introductio geographia» (1533). Апиан несколько раз использовал эту ксилографию и в других работах. Монтировки телескопов из более поздней истории астрономии многим обязаны традиции изготовления торкветумов (пример наиболее убедительного подтверждения этого см. на ил. 163 на с. 536).
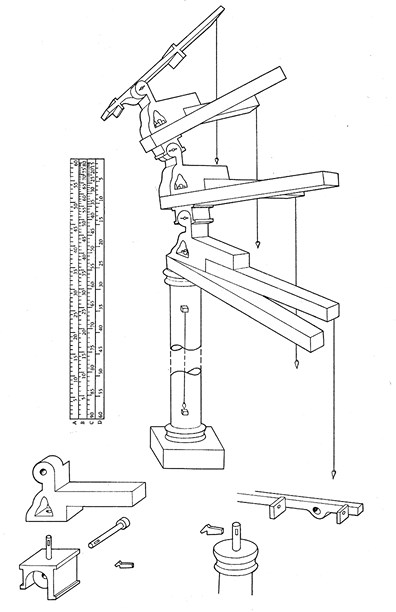
104
Ректангулус Ричарда Уоллингфордского. Каждая из трех пар линеек раздвигается на манер ножниц, причем две верхние пары и визирное плечо на верхушке вращаются под прямым углом к плоскости вращения нижней пары. К каждой из линеек подвешен отвес, как показано на рисунке. На сопроводительных рисунках представлены детали основной конструкции. Пластина со шкалами показывает, каким образом должны быть градуированы линейки, чтобы можно было измерить углы между ними с помощью нитей, в некоторых случаях подвешенных под прямыми углами к своим линейкам.
Самой важной завершенной работой был его «Трактат об Альбионе». Альбион («all by one» – все в одном) – во многих отношениях наиболее примечательное изобретение из всех разновидностей средневековых экваториумов. Понять его устройство значительно сложнее, поскольку в нем не воспроизводилось напрямую движение планетных кругов, а каждому из них соответствовал металлический эквивалент, как это делалось в большинстве предшествующих конструкций. Взамен этого в нем использовались диски, содержавшие табличную информацию и позволявшие получать планетные уравнения, которые затем должны были прибавляться к (или вычитаться из) среднему движению посредством вращения дисков под соответствующими углами. Это предполагало использование неравномерно градуированных шкал; и для того, чтобы удлинить внешнюю шкалу дисков, Ричард придал некоторым из них форму спирали. В принципе, спираль могла иметь неограниченное количество витков – до тридцати и более. Роль указателя играла нить, продернутая через центр. В целом изделие очень похоже на круговые счетно-логарифмические линейки – инструменты, отошедшие в прошлое примерно в то время, когда изобрели электронные калькуляторы, то есть в 1970‐х гг. Альбион насчитывал в совокупности более шестидесяти шкал, некоторые из них – овальные. Их комплектность не определялась единым алгоритмом и зависела от различных методов нанесения делений. Инструмент объединял в себе два различных типа астролябий (один из них – «сафея»), но не они определяли его главные качества. Не существовало практически ни одной задачи классической астрономии, которая не могла бы быть решена с помощью альбиона. Используя его в качестве подручного средства, можно было определять не только положения планет, но и параллаксы, скорости, соединения, оппозиции, а также предсказывать затмения Солнца и Луны.
Гораздо проще понять другую разновидность экваториума, представлявшего собой простую аналогию планетных моделей. По этой причине он получил более широкое распространение, хотя его возможности были в значительной степени ограничены. Отсутствие непосредственного сходства с реальностью снискало альбиону большое уважение сначала в Англии, а затем и в южной Европе, и он оставался в моде вплоть до XVI в., приобретая самые разнообразные формы, благодаря неизвестным авторам-изготовителям. С его использованием написано по меньшей мере семь трактатов, и астрономы начали преобразовывать его в другие подручные инструменты, особенно в параллактические и те, что помогали прогнозировать затмения. Около 1430 г. венский астроном Иоганн Гмунден изготовил инструмент, воспроизводившийся, по всей видимости, наиболее часто. Региомонтан переписал трактат Ричарда и подготовил его весьма небрежное переиздание. На его основе Иоганн Шёнер изготовил свой инструмент для предсказания затмений. Наиболее талантливой печатной работой, содержащей инструкции по его применению, был трактат «Astronomicum Caesareum» (1540), написанный Петером Апианом из Ингольштадта, о котором мы уже упоминали ранее (см. ил. 102) как о собрании относительно ясно изложенных печатных описаний экваториумов.
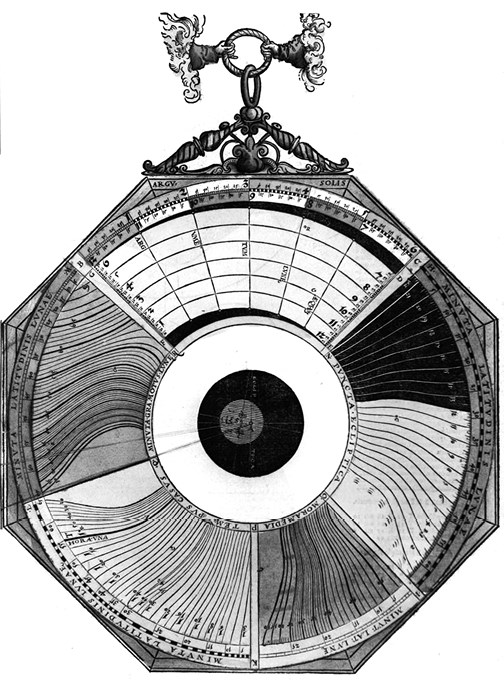
105
Один из многих инструментов из книги Петера Апиана «Astronomicum Caesareum» (1540), с помощью которого одна из астрономических величин может быть рассчитана как функция двух других или более. Приспособления подобного рода имеют долгую историю в астрономии.
Последующие авторы извлекли из работ Ричарда определенные основополагающие принципы (у нас нет возможности объяснить их здесь в деталях, но они касались графического представления функциональных зависимостей) и углубили их, применив методы, существенным образом повлиявшие на последующую историю. Во Франции, начиная с 1526 г., математик и космограф Оронс Фине написал несколько трактатов об экваториумах и простейших способах их применения; то же самое (и примерно в это же самое время) сделал Франциско Сарсоса из Арагоны; было и несколько других примеров демонстрации подобного рода изощренных технических приемов, которые в последующие века получили название «номография». Определенное представление о процедурах, применяемых в такого рода инструментах, можно получить из ил. 105, взятой из «Astronomicum» Апиана. Тщательно исполненная печатная работа Апиана навлекла на себя впоследствии весьма поверхностную критику Кеплера, назвавшего ее пустой тратой времени и дарования. Однако в ее цели не входило доставить удовольствие респектабельному Кеплеру, который, если уж на то пошло, был заинтересован в поиске не столько способов облегчения вычислений, сколько императорского покровительства.
Назад: АСТРОНОМЫ-ПРАКТИКИ
Дальше: ЧАСЫ И МИРОЗДАНИЕ

