Книга: Космос. Иллюстрированная история астрономии и космологии
Назад: НЕПОДВИЖНЫЕ ЗВЕЗДЫ У ПТОЛЕМЕЯ
Дальше: АСТРОЛОГИЯ: ВЛИЯНИЕ ПТОЛЕМЕЯ
ПТОЛЕМЕЙ О ПЛАНЕТАХ
В девятой, десятой и одиннадцатой книгах «Альмагеста» объясняется, каким образом можно рассчитать долготы планет – нижних (Меркурия и Венеры) и верхних (Марс, Юпитер и Сатурн). Как мы показали в главе 3, для этого нужно использовать две разных схемы расположения эклиптики по отношению к деференту, и поскольку Меркурий вызывает определенные, присущие только ему трудности, то для этой планеты требовалось ввести дополнительные уточнения. Здесь мы снова приведем только итоговые результаты работы Птолемея. В данном случае он располагал гораздо меньшим количеством надежных данных, полученных от предшественников, чем в случае Солнца и Луны. В его распоряжении были, конечно, концепция эпицикла и – через посредство Гиппарха – некоторые вавилонские периодические соотношения, типа «за 59 лет Сатурн дважды возвращается на исходную долготу и 57 раз – в исходную аномалию (эквивалентную точке стояния в начале попятного движения)». Эти периодические соотношения дали ему возможность построить таблицы средних движений, хотя впоследствии ему понадобилось подкорректировать их с учетом выработанных им моделей.
Вероятно, здесь уместно будет добавить, что Птолемей указал два различных подхода, позволяющих очень точно определять средние планетные движения. В дополнение к упомянутому здесь пояснению он отметил далее возможность их получения напрямую из наблюдений в течение продолжительного времени. В принципе, они могли бы быть найдены таким способом, однако, как легко показать, это вряд ли можно было осуществить на практике. Что касается согласования параметров, полученных им из периодических соотношений, то в отдельных случаях это сделано на основе производимых им наблюдений, однако в случае Меркурия и Сатурна наблюдения, на которые он ссылается, не соответствовали выведенным из них, по его утверждению, средним движениям.
62
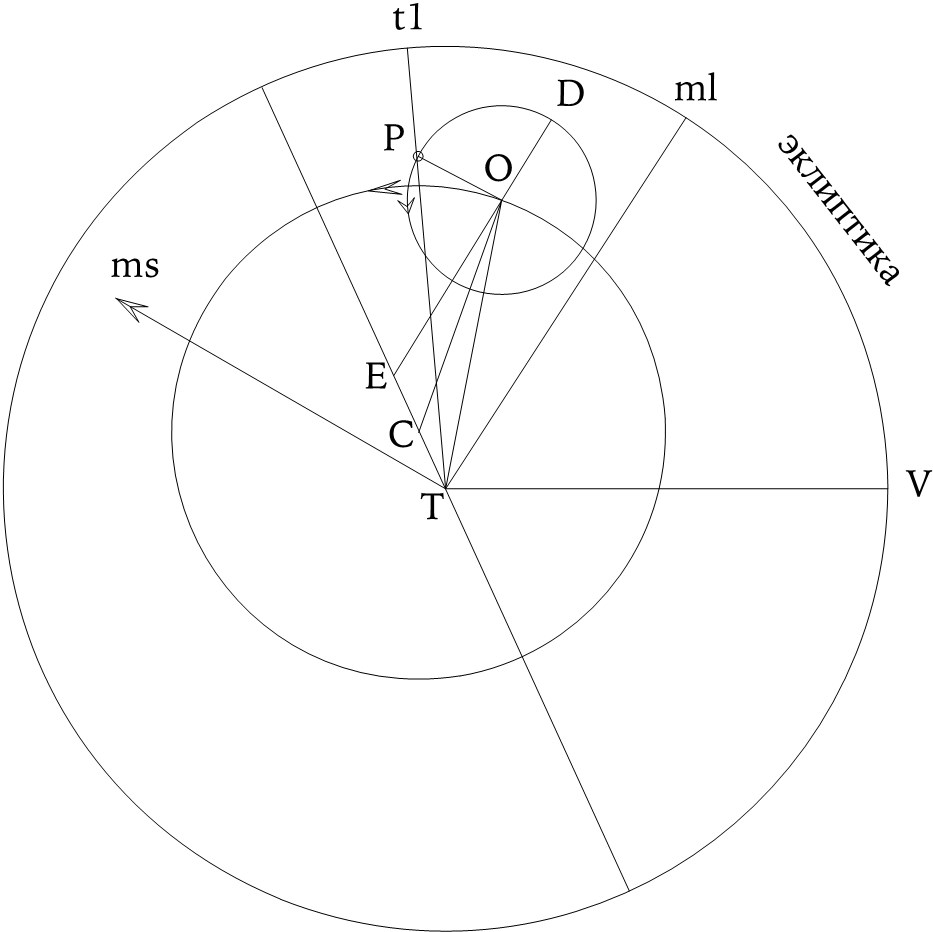
Модель Птолемея для внешних планет
Солнце, как мы уже видели, хорошо вписывается в эпициклические теории. (По поводу современных представлений об этом предмете см. с. 74 выше.) Если не вдаваться в подробности, то для нижних планет среднее Солнце является центром эпицикла, в то время как для верхних планет радиус эпицикла, несущего на себе планету (отрезок OP на ил. 62), всегда параллелен линии, соединяющей Землю со средним Солнцем (ms). Следует отметить, что на этом рисунке, где C – это центр круга деферента, добавлена еще одна точка E, находящаяся на линии, соединяющей T и C, и отстоящая от C на таком же расстоянии, как и T, но по другую сторону. Эта точка – так называемая точка экванта – позволила Птолемею ввести еще одну аномалию. До этого всегда предполагалось равномерное движение эпицикла вокруг центра деферента. (Аполлоний, можно предположить, думал иначе, но это – спорный вопрос.) Пытаясь вывести размер эпицикла, Птолемей обнаруживает, что он, скорее всего, меняется по закону, не удовлетворяющему обычной гипотезе об эксцентрическом круге деферента. Поэтому он вносит поправку в его угловую скорость, делая ее постоянной не относительно C, а относительно E. (На ил. 62 линия EO параллельна линии, проходящей через T и ml, обозначающей среднюю долготу.)
Введение понятия экванта было тем более похвально, так как оно намечало перелом в традиционной догме, когда все должно объясняться в категориях равномерного кругового движения. Птолемей ввел круг экванта (он не показан на ил. 62), находясь на котором точка, лежащая на продолжении линии EO, вращалась с постоянной скоростью. Это должно было уберечь его от критики, но не уберегло, и четырнадцать столетий спустя мы обнаруживаем, что даже Коперник находил гипотезу экванта безвкусной. Вкус, без сомнения, относится к категории вещей, на формирование которых приходится тратить много времени.
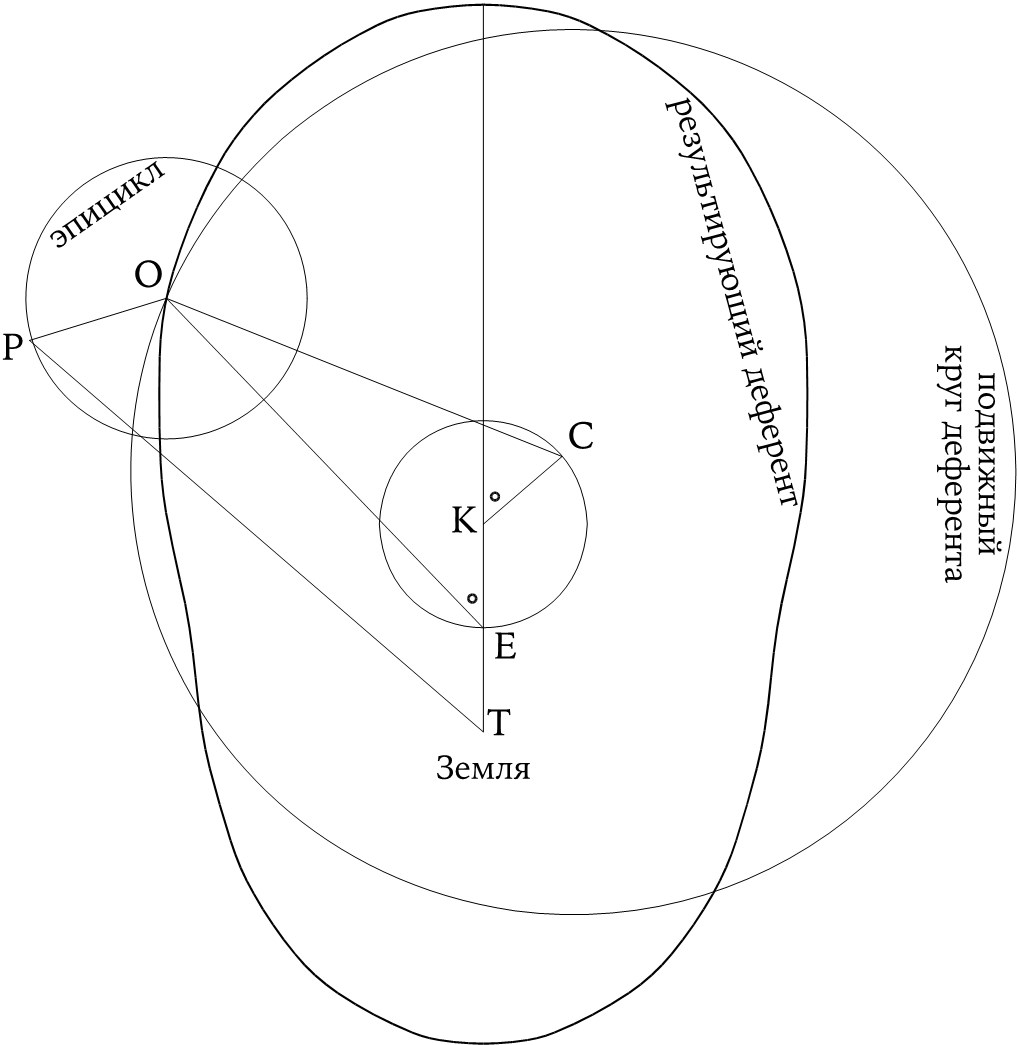
При переходе к Венере и Меркурию роли эпицикла и деферента меняются местами по ранее разобранным нами причинам. Венера обладает большим эпициклом, но в остальном ее движение достаточно легко поддается объяснению. А вот модель, разработанная для Меркурия, представляет нам Птолемея во всей его гениальности. Она включает в себя все встречавшиеся нам до этого идеи. Например, в ней есть центр экванта, представленный на ил. 63 точкой E; есть эпицикл, движущийся по кругу деферента, однако теперь центр деферента C также является подвижным. Мы уже сталкивались с подобным приемом в модели расчета долготы Луны, но в данном случае центром малого круга, по которому движется точка C, является не точка T, а точка K, расположенная на таком расстоянии от E, чтобы отрезок KE был равен отрезку TE. Положение точки C в определенный момент времени задается работой двух углов, отмеченных на рисунке маленькими кружками. То есть они движутся по кругу с постоянной скоростью, но в противоположных направлениях. Птолемей пришел к этой сложной модели, руководствуясь ошибочными наблюдениями, которые натолкнули его на мысль, что у Меркурия имеется два перигея, и ни один из них не находится напротив апогея; они располагаются в точках, отстоящих примерно на 120° от того места, где, предположительно, должен быть нормальный перигей. Вне зависимости от качества его наблюдений, он фактически способствовал возникновению планетной астрономии, где впервые появляется такая фигура, как овал. Каждому положению точки C соответствует строго определенное положение точки O, и траектория точки O является, по сути, результирующей кривой деферента, по которому движется эпицикл. Ее форма показана на рисунке в виде жирной линии (масштаб не соблюден). Некоторые астрономы XIII в. называли ее «шишкой»: она представляет собой стянутый по бокам овал и, в силу наличия небольшого эксцентриситета, очень близка к эллипсу.
63
В довольно сложной модели Птолемея для Меркурия центр круга деферента (C) движется таким образом, чтобы углы с вершинами в точках E и K, отмеченные специальными кружочками, были равны друг другу. Если придерживаться этого правила, то центр эпицикла будет вычерчивать овал, и, коль скоро бы Птолемей захотел, то он мог бы определить эту фигуру как единственную в своем роде стационарную кривую деферента. Некоторые средневековые мастера, специализирующиеся на изготовлении инструментов, так и поступали, но почтение, выказываемое в отношении правильных кругов как обязательного атрибута приемлемой теории, в общем и целом работало против этой идеи.
Птолемей занимался рассмотрением меняющихся планетных движений, доступных для непосредственных наблюдений, однако, помимо этого, он хотел упростить процедуру их расчета для произвольного момента времени, будь то прошлое, настоящее или будущее. Для этого он выработал ряд правил, которые могли шаблонным образом применяться даже неопытными людьми. Бегло ознакомившись со всеми описанными здесь моделями, можно констатировать, что мы имеем ситуацию, когда каждому «среднему движению» – то есть углу, увеличивающемуся с постоянной скоростью, – соответствует другой, немного отличающийся от него угол, который требуется использовать при переходе от составляющих углов к итоговой истинной долготе. Мы впервые столкнулись с этими небольшими отклонениями (так называемыми уравнениями) в солнечной модели. Для упрощения расчетных действий Птолемей составил таблицы средних движений, сопроводив их другими, особыми таблицами, содержащими уравнения. Некоторые из них – это просто функции средних движений, но были и значительно более сложные, требующие введения в вычисление промежуточных членов. Однако в итоге, для получения конечного результата, от астронома требовалось всего лишь прибавить или вычесть соответствующий угол. Но даже в этом случае для расчета положения всех планет на какой-то определенный момент времени, подготовленному астроному требовалось потратить один или два часа, и еще большее время требовалось для определения широт планет.
В тринадцатой книге «Альмагеста» Птолемей ввел в теорию широ́ты – примерно по той же схеме, как это он сделал для Луны. Таким образом, к ранее изложенному в двумерном виде было добавлено третье измерение. Птолемей расположил плоскость планетного деферента под углом к плоскости эклиптики. В случае верхних планет угол наклона оставался неизменным, но для нижних планет ему пришлось сделать его осциллирующим в соответствии с правилами, формулировка которых стоила ему немалых усилий. Затем ему понадобилось расположить в разных плоскостях еще и эпициклы, и здесь он опять изобретает правила их осцилляции для внутренних планет, на сей раз по отношению к плоскости деферента.
Несложно понять причину, почему проблема широты была столь сложна и столь принципиальна для Птолемея и всех других сторонников системы, в центре которой находится Земля. Она заключалась в том, что физически плоскости планетных орбит проходят не через Землю, а через Солнце (поскольку гравитационные силы, действующие на планеты, направлены к Солнцу). Он мог бы частично компенсировать это невидимое препятствие, если бы сделал плоскости эпициклов параллельными плоскости эклиптики. Вне всяких сомнений, огромная его заслуга заключается в том, что он таки сделал это в целях упрощения, когда писал свою позднюю работу «Подручные таблицы», где зафиксировал углы наклона эпициклов Меркурия и Венеры, уточнив присвоенные им ранее значения. К сожалению, он решил сделать постоянными и наклоны эпициклов внешних планет, а это привело к неустранимым ошибкам, хотя позже он исправил данный недочет в своей работе «Планетные гипотезы». (Мусульманские, а затем и западные астрономы следовали в этом вопросе, да и во многих других, правилам, изложенным Птолемеем в «Альмагесте», так что его профессиональные метания почти не оставили никакого следа в истории.) В «Подручных таблицах» можно найти только процедуры, которым нужно следовать, применяя указанные модели, но сами модели никак не доказываются, поэтому у нас нет возможности установить, каким образом он сделал свое открытие. Однако и здесь, и во многих других местах мы видим следы высочайшего гения Птолемея в вопросах отбора и анализа астрономических наблюдений для подкрепления теоретических соображений. Астрономия включает множество других моментов, однако в этом, в высшей степени важном, аспекте Птолемей просто не имел себе равных вплоть до того времени, когда Иоганн Кеплер приступил к анализу наблюдений Тихо Браге.
Невозможно объяснить в двух словах, как параметры отдельно взятой модели могут быть выведены из имеющихся наблюдений, однако некоторые очень краткие общие замечания вполне допустимы. Во-первых, очень важно отдавать себе отчет в том, насколько актуальны такого рода процедуры для любой солидной эмпирической науки, а также в том, насколько редко они встречаются в дошедших до нас документах из столь раннего периода. В «Альмагесте» Птолемей широко использовал наблюдательные данные, однако он начинал не с чистого листа, если можно так выразиться, многие данные он унаследовал от предшественников, и иногда бывает сложно понять, какие из них получены им самостоятельно. В отдельных случаях выданное им за данные собственных наблюдений, было, скорее, подгонкой к заранее известному конечному результату. К тому же дело осложнялось тем, что иногда он располагал гораздо бо́льшим количеством данных, чем ему требовалось на самом деле. Оставляя в стороне все эти соображения, мы можем сказать: предложенная им методика обладала непреходящей ценностью. Закладывая основы общего понимания модели, которую ему нужно было применить к отдельным планетам, он столкнулся с необходимостью ввести понятие углового движения (например, движения в деференте и в эпицикле) и установить относительный масштаб кругов. Если исходить из предположения, что движение является круговым и равномерным, а потому углы, отсчитываемые относительно центра, пропорциональны времени, то нахождение параметров модели предполагает как минимум решение следующей геометрической задачи: нахождение по трем заданным точкам, расположенным на круге, другой точки – внутри круга или вне его – из которой линии, соединяющие ее с этими тремя точками, будут образовывать заданные углы (в случае астрономии именно они и будут являться наблюдаемыми углами). Аполлоний, как считается, решил эту общую геометрическую проблему и сделал это не только эмпирическим путем. Гиппарх, определенно, применял ее к Солнцу и Луне. Астрономы более позднего периода внесли отдельные усовершенствования, поняв, что решение получается более простым, если осуществлять наблюдения в заданный момент времени. Например, если наблюдать Солнце в дни равноденствий и солнцестояний, то углы будут прямыми. В случае Луны, следуя Гиппарху, но исправив предварительно некоторые его расчетные ошибки, Птолемей для точного определения лунных параметров использовал тройки лунных затмений, поскольку в этом случае Земля расположена на одной линии с Солнцем и Луной. Птолемей мастерски осуществил отбор множества других особых случаев, упрощавших решение, и маленькой (хотя и объяснимой) трагедией позднейших астрономов было то, что они слишком часто не уделяли должного внимания методологии Птолемея, предпочитая безоговорочно использовать полученные им многочисленные решения.
Назад: НЕПОДВИЖНЫЕ ЗВЕЗДЫ У ПТОЛЕМЕЯ
Дальше: АСТРОЛОГИЯ: ВЛИЯНИЕ ПТОЛЕМЕЯ

