Книга: Космос. Иллюстрированная история астрономии и космологии
Назад: ВЗАИМОСВЯЗЬ ГРЕЧЕСКОЙ ГЕОМЕТРИИ И АСТРОНОМИИ
Дальше: ГИППАРХ И ДВИЖЕНИЕ СФЕРЫ ЗВЕЗД
АПОЛЛОНИЙ И ПЕРЕХОД К ТЕОРИИ ЭПИЦИКЛОВ
Аполлоний из Перги (в прошлом Перга – сегодня обычно произносят «Перге» – античный греческий город на юге Малой Азии) жил во второй половине III – начале II в. до н. э. Он бывал в Александрии. Представляется сомнительным, что он (как шестью столетиями позже утверждал Папп) провел там долгое время, обучаясь вместе с другими учениками Евдокса, но не вызывает сомнений, что он был одним из величайших математиков греческой Античности, сопоставить с которым можно, пожалуй, только Архимеда. Его вклад в геометрию конических сечений (парабола, гипербола, пара прямых, окружность и эллипс) был примерно таким же, как вклад Евклида в элементарную геометрию. Он написал собственное сочинение (его бо́льшая часть основывалась на достижениях предшественников), опираясь на строгий логический метод. Кроме того, он показал, каким образом можно строить кривые, используя методы, очень близкие к используемым в современной аналитической геометрии. Чрезвычайная полезность этих методов в астрономии выяснилась в эпоху Кеплера, Ньютона и Галлея, каждый из которых скрупулезно изучал труды Аполлония.
Интерес Аполлония к астрономии подтверждается множеством косвенных упоминаний. По сообщению одного из авторов, у него было прозвище Эпсилон, поскольку эта греческая буква (ε) внешне напоминала Луну, изучением которой он занимался наиболее интенсивно. В другом источнике говорится, что, согласно его данным, расстояние между Луной и Землей составляет 5 миллионов стадий (около 0,96 миллиона километров), а это примерно в два с половиной раза больше реального. Другой автор, астролог Веттий Валент, расцвет его деятельности пришелся на 160 г. н. э., утверждал, что пользовался таблицами Солнца и Луны, составленными Аполлонием; однако, вероятнее всего, автором таблиц был его однофамилец. Но самое интересное упоминание, относящееся к его астрономическим изысканиям, связано с его теоремой из теории планетных движений. Согласно Птолемею, Аполлоний обнаружил связь между скоростью планеты, движущейся в эпицикле, скоростью центра этого эпицикла, обращающегося по кругу деферента, и двумя расстояниями на рисунке, отображающем положение, когда планета кажется неподвижной, меняя прямое движение на попятное. (См. пояснение этой терминологии в предпоследнем разделе предыдущей главы, где указанные представления были введены с некоторым опережением по отношению к занимаемому ими месту в истории.)
51
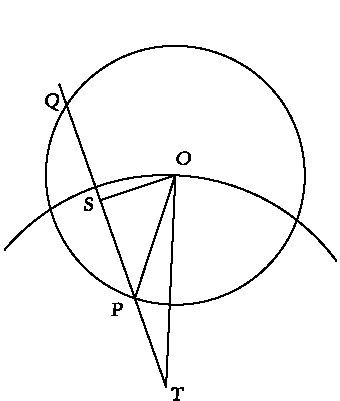
Иллюстрация теоремы Аполлония об эпициклическом движении
Описанная конфигурация изображена на ил. 51, где точка O – центр эпицикла, а P – планета. Последняя представляется неподвижной для наблюдателя, находящегося на Земле, обозначенной здесь точкой T. Движение точки P под прямым углом к лучу зрения TQ должно складываться из двух равных и противоположно направленных компонент: одна возникает в силу того, что планете передается скорость точки O, а другая является результатом ее вращения вокруг O и направлена вдоль касательной к эпициклу в точке P. Если разложить эти скорости, то, используя простейшие методы современной геометрии, можно легко получить доказательство следующей теоремы: отношение угловой скорости в деференте к скорости в эпицикле относительно отрезка OT равно отношению PS к PT. (Здесь PS является серединой хорды QP.)
Тот же самый результат можно получить с помощью метода пределов из классической геометрии. Это сделал Птолемей в «Альмагесте» спустя более чем триста лет. Вне зависимости от того, какой метод использован самим Аполлонием, представляется вполне очевидным, что он обладал навыком анализа движения в двух измерениях. Это довольно важно, поскольку если это так, то он был ключевой фигурой на первом этапе разработки идеи эпициклического движения. По утверждению Птолемея, когда он доказывал приведенные выше соотношения, он сделал это как для эпициклического (показано выше), так и для другого, эквивалентного ему представления, где планета движется по траектории, которую мы сегодня назвали бы подвижным эксцентрическим кругом.
52
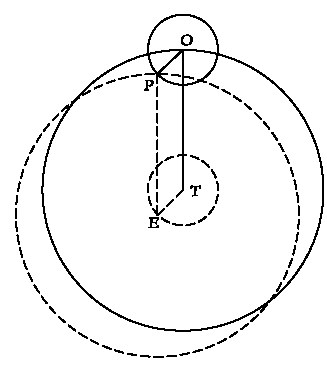
Эквивалентность определенных типов эксцентрического и эпициклического движений
В эквивалентности этих моделей легко убедиться с помощью ил. 52, где сплошные линии обозначают эпициклическое движение, а пунктир – альтернативное представление. Забудем на время про пунктир. Для попадания в точку P из точки T нужно, очевидно, сначала переместиться в точку O, а затем – в P; или же сначала в точку E по отрезку TE, равному и параллельному отрезку OP, а затем в точку P по отрезку EP, который равен и параллелен отрезку TO. Равенство длин упомянутых здесь отрезков означает, что точки E и P лежат на кругах, изображенных пунктиром, как показано на рисунке. Точку E обычно называют эксцентрической («вне центра») точкой, а внешний пунктирный круг – эксцентрическим кругом. Сам этот круг, надо отметить, подвижен.
С чисто геометрической точки зрения не имеет значения, каким образом производится разделение движения по большим и малым кругам, в силу чего эти два построения являются эквивалентными, и единственное, что вынуждает нас вносить различие в эти понятия, – это исторические причины.
Эксцентрические круги, с ними мы еще встретимся, когда будем рассматривать позднейшие модели, есть не что иное, как фиксированные круги, центр которых находится в точке, не совпадающей с Землей. И здесь будет уместно заметить: они действительно могут рассматриваться как особый тип эквивалентного представления эпициклического движения. Пусть центр большого круга на ил. 52, нарисованного сплошной линией, зафиксирован в точке T, то есть связан с Землей. Если по мере движения точки O по большому кругу отрезок OP будет всегда параллелен отрезку TE, то точка P будет лежать на фиксированном эксцентрическом круге (он изображен на рисунке в виде большого пунктирного круга) с центром в точке E.

