Картезианские поиски правдоподобной теории гравитации ни к чему не привели. Существовал и другой способ главным образом качественного космологического размышления, который развивался параллельно с картезианством и время от времени пересекался с ним; это была расширенная трактовка магнитной философии Гильберта и Кеплера. Она сохранилась и активно использовалась в течение довольно долгого времени в Англии, где ее жизнеспособность поддерживалась благодаря главным образом дискуссионным группам, сосредоточенным в первую очередь в Грешем-колледже в Лондоне, а позже – в Королевском обществе. И Джон Уилкинс, и Кристофер Рен были выразителями идей Гильберта. В 1640 г. Уилкинс опубликовал две общедоступные и вместе с тем информативные книги, в которых рассматривалась возможность путешествия на Луну; обе они в той или иной степени пропагандировали воззрения Гильберта и Кеплера и назывались «Рассуждение о новой планете» и «Открытие лунного мира». В 1654 г. последователь Уилкинса Уолтер Чарльтон опубликовал эти идеи, объединив их с атомизмом Гассенди. Несмотря на это, было бы сложно представить, чтобы без участия таких специалистов, как Рен, Эдмонд Галлей и Роберт Гук, английские дискуссии продолжали бы фокусироваться на законах, задающих точную форму орбит и их связь с законами механики – такими, как закон инерции и одна из разновидностей закона центральной силы тяготения (в направлении Солнца).

Дискуссию стимулировало появление кометы 1664 г. В это время Рен являлся савилианским профессором астрономии в Оксфорде, а Джон Уоллис – савилианским профессором геометрии. Уоллис развивал кометную теорию Хоррокса, который анализировал движение кометы 1577 г., считая его прямолинейным, но видоизмененным магнитным воздействием Солнца. Теперь Рен пытался вывести новую кометную орбиту, основываясь на четырех измерениях, полагая вслед за Кеплером, что она движется по прямой линии с постоянной скоростью.

Не прошло и месяца, как появилась вторая комета, послужившая дополнительной встряской для начавшего было угасать интереса к этой проблеме, решить которую оказалось не под силу ни одной из заинтересованных сторон. Гук опробовал гипотезу кругового движения, но предпочел иметь дело с линейной альтернативой с учетом солнечного притяжения того или иного вида. Он высказал предположение, что оно должно быть либо всепроникающим, либо осциллирующим с колебаниями, затухающими по мере увеличения расстояния от Солнца. Этот механизм содержал некоторые заимствования из декартовской идеи вихревого эфира, но имел гораздо больше общего с законом центральной силы притяжения, обсуждавшимся Гуком со своими друзьями в Королевском обществе.

Гук, будучи куратором экспериментов общества, как раз начал в это время долгую серию экспериментов с гравитацией. Прошло десять лет, и если сравнивать с появившимися вскоре теориями Ньютона, ему так и не удалось добиться заметного теоретического прогресса; тем не менее мы можем использовать его как пример, иллюстрирующий изменение отношений к старой аристотелевской Вселенной. С точки зрения Гука, оглашенной им во время лекции 1670 г. (впервые опубликована в 1674 г.), все небесные тела обладают притяжением или гравитационной силой, направленной к их центрам, удерживающей вместе отдельные их части, а также воздействующей на другие небесные тела, которые попадают «в пределы сферы их действия». Эта последняя оговорка предполагает, что он считал возможным уменьшение указанной силы до нуля на некотором конечном расстоянии и признавался: он еще не сумел установить закон этой силы, и ничего не сказал о ее сущности.

В 1677 г. или около того Ньютон обсуждал эти вопросы с Реном, полагая, что Рен имел представление о законе, согласно которому сила убывает обратно пропорционально квадрату расстояния между притягивающимися телами. Его собственное сообщение о законе обратных квадратов было впервые опубликовано в «Principia mathematica philosophiae naturalis» («Математические начала натуральной философии», обычно называемые просто «Principia»; 1687). Скорее всего, он окончательно убедился в его истинности лишь за три года до этого, но указанный закон был только одной частью сложной головоломки, и для того, чтобы собрать остальные, нам нужно принять во внимание более ранние этапы его карьеры.

Исаак Ньютон родился на Рождество 1642 г. в Вулсторпе (графство Линкольншир). Его отец умер до его рождения, и свои молодые годы он провел вместе с бабушкой, так как его мать вышла замуж за священника, который, по всей видимости, не питал особой любви к Исааку. В 1661 г., после окончания школы в Грэнтеме, он поступил в Тринити-колледж Кембриджского университета, а спустя четыре года вернулся домой, поскольку университет закрылся из‐за вспышки эпидемии чумы. Уже тогда он начал проявлять интерес к текущим математическим и научным вопросам. Он много читал (математику он изучал по работам Декарта и Уоллиса), и перерыв, возникший из‐за чумы, дал ему время на то, чтобы совершить определенное количество собственных оригинальных открытий. К 1669 г. он уже обладал квалификацией, которая позволила ему унаследовать от Исаака Барроу должность Лукасовского профессора математики в Кембридже. Он часто посещал собрания Королевского общества, но окончательно покинул Кембридж только в 1696 г., когда его сделали смотрителем Монетного двора. Он умер в 1727 г., будучи видным национальным деятелем и человеком с непревзойденной международной научной репутацией. Он много писал о религии и о других самых разных предметах, не имеющих прямого отношения к областям, в которых он оставил по себе наибольшую память, а именно – в математике, физике (особенно в оптике) и теоретической механике. Именно эти предметы позволили ему оказать наиболее существенное влияние на ход развития астрономии.

Одна из студенческих записных книжек Ньютона, начатая в 1661 г., содержит свидетельства его осведомленности о третьем законе Кеплера и о некоторых результатах наблюдений Хоррокса, и изучения им методов определения положений планет, приведенных в «Astronomia Carolina» Томаса Стрита. К 1664 г. он подправил работу Декарта, посвященную «сохранению движения» (необходимо, смекнул он, принимать во внимание направления «движений»), и разработал теорию центробежной силы, независимо предложенную Гюйгенсом в 1673 г. Объединив ее с третьим законом Кеплера, он применил ее к случаю Луны, расстояние до которой он оценил в шестьдесят земных радиусов, и к объекту, находившемуся на земной поверхности (предположим, речь идет о знаменитом упавшем яблоке). Проделав эту работу, он подкрепил свою раннюю догадку о том, что сила, действующая на эти тела, уменьшается обратно пропорционально квадрату расстояния.

Но его данные отличались неполнотой и не подтверждали эту идею столь основательно, как ему хотелось бы, и, скорее всего, именно это было причиной того, что он откладывал окончательное решение вопроса в течение двадцати лет (на деле, до 1685 г., когда он взялся за написание своих «Principia»). В этот период, как известно, он изучал Борелли, писавшего в 1666 г., что изогнутые траектории планет предполагают существование центробежной силы, которую можно рассматривать как равную и противоположную силе притяжения со стороны центрального тела. Этот отрывок очень хорошо сочетался с его собственными догадками, но остается невыясненным, содержал ли он в себе что-то новое для Ньютона или нет.

Ньютон познакомился с Кеплеровым законом площадей в самом конце 1670‐х гг. или даже после 1680 г., когда уже в полной мере освоился со своими недавно разработанными динамическими законами. Это обстоятельство в сочетании с обменом корреспонденцией с Гуком натолкнуло его на мысль, давшую затем крайне результативные последствия. Гук хотел найти закон центральной силы, которая превращает прямолинейное движение планеты в движение по эллипсу, и в этом он был похож на Кеплера, тоже говорившего о движении планет по эллипсу. Ньютон располагал всеми необходимыми инструментами (а именно – методами разработанного им исчисления бесконечно малых и своими динамическими идеями) для демонстрации следующего: закон площадей предполагает то, что сила и в самом деле направлена к единому центру и она обратно пропорциональна квадрату расстояния. Обязательным шагом на этом пути было доказательство того, что однородная материальная сфера вызывает в точности такую же силу гравитации, как если бы вся ее масса располагалась в центре.

В декабре 1684 г. Ньютон попросил Флемстида предоставить ему данные о расстояниях и периодах спутников Юпитера, и Флемстид ответил, что, на самом деле, они полностью согласуются с третьим законом Кеплера – законом, связывающим период с размером орбиты. Кроме того, Ньютон спросил, есть ли какие-нибудь основания полагать, что он прав в своем интуитивном ощущении: Юпитер может возмущать орбиту Сатурна. Флемстид пояснил некоторые ошибки, обнаруженные им в параметрах Кеплера для этих планет. Ньютон остался доволен обоими этими ответами, поскольку из первого ответа следовала возможность пренебречь влиянием Солнца на спутники, а второй ответ означал, что данные Кеплера не безупречны, и это, как он полагал, освобождало его от обязательства учитывать другие виды сил, кроме гравитационной. По меньшей мере их существование не могло быть доказано на основании данных, полученных Кеплером.

В 1684 г. ученый мир стал понемногу понимать накопленное Ньютоном интеллектуальное наследие. Галлей приехал в Кембридж спросить его о том, по какой траектории будет двигаться планета, если на нее действует сила, обратно пропорциональная квадрату расстояния. Рен, Гук и он сам, пояснил Галлей, не смогли решить эту проблему. Ответ Ньютона заключался в следующем: это должен быть эллипс, и хотя он еще не сумел найти доказательства, он обязательно пришлет его Галлею в скором времени. (После переписки с Флемстидом он пришел к выводу, что кометная орбита параболическая; данный результат тоже следовал из закона обратных квадратов и являлся не менее важным выводом.) Это побудило Галлея, после знакомства с некоторыми выдающимися работами Ньютона по механике, понудить Ньютона к их публикации. Так появились «Principia», написанные в рекордно короткие сроки.

Не успела книга выйти в свет, как сразу же возникло большое количество споров по поводу приоритета. Гук выступил с громким протестом, утверждая, что именно ему принадлежит приоритет в применении закона обратных квадратов к решению обсуждаемой проблемы. Он действительно долго размышлял о критических замечаниях, высказанных Буйо в отношении суждений Кеплера по этому вопросу. Он отверг идею Буйо, согласно которой свет не является ни телом, ни веществом, а представляет собой своего рода геометрического посредника между ними. Согласно Гуку, свет, напротив, полностью телесен, и движение частиц светящегося тела вызывается его источником. Он много писал, руководствуясь этими выразительными, импрессионистскими аксиомами. В 1685 г. он сочинил несколько рассуждений о том, каким образом можно объяснить гравитацию через «непрерывный импульс», исходящий из центра Земли, влияние которого уменьшается обратно пропорционально квадрату расстояния. Его модель была не нова, она основывалась на как бы разреживании света в обратной пропорции к площади основания светового конуса, и до начала борьбы за приоритет, он, по всей видимости, относил ее к расхожим истинам, известным по меньшей мере начиная с Кеплера. Такое объяснение он нашел для земной гравитации; но когда он начал применять аналогичные идеи к Солнцу, то предложил заменить этот закон законом обратных четвертых степеней. Как он ни старался, ему так и не удалось приблизиться к объяснению результатов, полученных Кеплером. В письме к Галлею от 1686 г. Ньютон еще не проявлял особой грубости, он лишь обратил внимание на математические ошибки Гука и мягко указал: его доказательство и доказательство Гука являются всего лишь гипотезами. И Кеплер, сказал он, всего лишь высказал предположение о том, что его овалы являются эллипсами. И все же Ньютон уже мог подойти к решению этого вопроса, используя «правильный» закон силы.

Ньютон не упоминает имени Кеплера в своих «Principia» вплоть до третьей книги, но это никак нельзя назвать утаиванием истинных намерений. Как отметил Галлей в своей рецензии на «Principia», первые одиннадцать теорем Ньютона находились в полном согласии с «явлениями небесных движений, установленными величайшей проницательностью и усердием Кеплера». Третья книга «Principia» называлась «Система мира», и есть все основания полагать, что это было самым первым полным объяснением движения материи во всей Вселенной под действием одного и того же набора физических законов. Движение планет и их спутников, комет, Земли и приливов ее морей – все это объяснялось с точки зрения всемирного тяготения. Планеты притягивают Солнце точно так же, как Солнце притягивает планеты. Вся материя притягивает всю другую материю и эта сила не зависит от типа материи. Значение имеет только «количество материи» и ее распределение. Он провел эксперименты с маятниками, сделанными из разных материалов, и не обнаружил никаких существенных различий в их механическом поведении.

Как мы видели на примере его переписки с Флемстидом, он понимал, что сила притяжения между центральным телом и планетой существенно больше, чем сила притяжения между самими планетами, но это последнее обстоятельство нельзя было полностью игнорировать, особенно когда планеты приближались друг к другу на кратчайшие расстояния. Другой важной нецентральной силой, которой также нельзя было пренебрегать, являлось возмущающее воздействие Солнца на Луну. Таким образом, важнейшая теория планетных возмущений вошла в небесную механику Ньютона уже в момент ее рождения.

Имея в своем распоряжении могучую динамику и теорию гравитации, Ньютон вполне мог объяснить сплюснутую форму Земли и то, что сила солнечного притяжения, действующая на ближнюю сторону ее выпуклого пояса, немного превышает силу, действующую на его дальнюю сторону. Это различие рождает вращательный эффект (пару сил), действующий на земную ось. Как он сумел показать впоследствии, этот двойной поворот приводит к прецессии, коническому движению земной оси, которое совпадает с прецессией точек равноденствия. Впервые в истории это явление было объяснено, исходя из физических законов.

В «Principia» много внимания уделено кометам и их, по сути, параболическим или эллиптическим орбитам. Ньютон понимал: кометы светят отраженным светом Солнца и пространство, в котором они движутся, не оказывает серьезного сопротивления их движению. О Ньютоне часто говорят, что он не был астрономом-наблюдателем, и астрономия, действительно, не его профессия, но он вполне квалифицированно дополнял собственные наблюдения наблюдениями других специалистов, собирая их из всех источников, которые он считал достоверными. В книге III «Principia» он показал, как можно по трем наблюдениям определить орбиту кометы, движущейся по параболе. Математическое обоснование его полуграфического решения этой «очень трудной задачи» не поддается краткому и простому изложению, но если взять в качестве примера комету 1680–1681 гг., то после составления таблицы из четырнадцати наблюдений Флемстида он пополнил ее семью своими превосходно выполненными наблюдениями, сделанными с помощью 7-футового телескопа, снабженного нитяным микрометром. Ученый получил свое теоретическое решение как раз тогда, когда выходило первое издание его книги (1686). Во втором издании, напечатанном в 1713 г., он повторно, вслед за Галлеем, пересчитал некоторые данные; а третье издание 1726 г. было пополнено еще несколькими галлеевскими расчетами, основанными на догадке о том, что эта комета является периодической и идентичной кометам, появлявшимся в 44 г. до н. э., 531 г. н. э. и 1106 г. н. э. Данное конкретное отождествление было опровергнуто в XIX в., но затем, как мы увидим далее, периодичность комет блестяще и исчерпывающе доказал Галлей в связи с другой кометой.

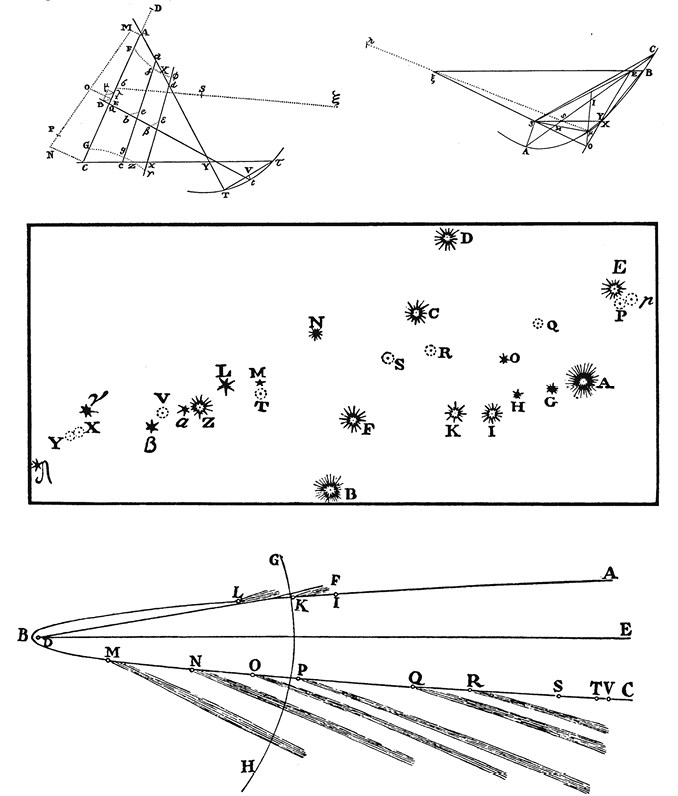
Наблюдения, произведенные Ньютоном, позволили ему заняться собственным анализом кометной траектории. Для начала он уточнил положения звезд в созвездии Персей, так как по нему проходила наблюдаемая кометная траектория. Его анализ основывался не только на траектории, но и на направлении хвоста, в отношении которого он проявил гораздо большую проницательность, чем его предшественники. Он, похоже, изготовил крупномасштабный рисунок траектории, где расстояние между Землей и Солнцем составляло около 41,5 сантиметра. (На ил. 167 это расстояние дуги GH от D.) В 1920‐х гг. А. Н. Крылов, оценивая точность полученных Ньютоном результатов, пришел к выводу, что она составляет более чем 0,05 миллиметра от используемой шкалы, а это во много раз превышало возможности описываемого метода. Каким бы ни было объяснение, нет никаких сомнений в том, что Ньютон удачно использовал наблюдения, проведенные в самых разных местах. К наблюдениям Флемстида и своим собственным он добавил наблюдения, произведенные Гуком и Джеймсом Паундом в Лондоне, а также другими наблюдателями в Италии, Нюрнберге, Восточной Индии, на Ямайке и в Бостоне (в американских колониях), и еще наблюдения Готфрида Кирха в Саксонии. Никогда еще кометы не подвергались такому серьезному и тщательному разбирательству. (Наверное, не лишне будет отметить, что Готфрид Кирх – представитель семейства, из которого вышло четыре хороших астронома, – был известен в свое время не только обширной перепиской с учеными из всех концов Европы, но и тем, что открыл несколько комет.)

Однако анализ Ньютона не закончился первоначальным замыслом воспроизведения «подлинного чертежа орбиты, описываемой данной кометой, и хвоста, испускаемого ей в некоторых местах». Он решил выяснить ее физические свойства и пришел к выводу, что кометы должны быть «твердыми, плотными, устойчивыми и прочными», иначе они не смогли бы сохраниться при прохождении в непосредственной близости от Солнца. Он посвятил десять страниц подробно аргументированного текста обсуждению строения комет и свойств их хвостов, с повторным привлечением самых разных сообщений, которые были взяты не только из Бразилии, но и из исторических источников, оставленных Аристотелем, «Саксонской хроникой», Матвеем Парижским и монахом Симеоном Даремским. Обсуждая физические свойства комет, он рассуждал, исходя не из субъективных предпочтений, а на основании нескольких экспериментов, которые он провел с тепловым воздействием летнего солнечного света на сухой грунт, рассчитав, что, находясь в перигелии, комета должна получать тепловой энергии «примерно в 2000 раз больше аналогичной энергии, идущей от раскаленного докрасна железа». Возникший в связи с этим вопрос о способности комет выдерживать такую температуру также был доведен им до числового решения. Тем не менее он не считал, что эти физические проблемы объяснены им полностью, и оставил их открытыми до проведения дальнейших исследовательских экспериментов, ясно сформулировав, что конкретно требуется определить. Это было сделано за много десятилетий до того, как другие специалисты всерьез занялись решением этой сложной задачи.

В числе наиболее захватывающих фрагментов работы Ньютона, по крайней мере с точки зрения тех немногочисленных экспертов, которые могли читать ее с пониманием, когда она впервые вышла в свет, были главы, посвященные движению Луны. Ньютон объяснил в общих чертах гравитационные причины известных на тот момент неравенств, касающихся лунного движения, движение узлов ее орбиты и причину, по которой она всегда повернута к нам одной стороной. Во втором и третьем изданиях он откликнулся на просьбу Галлея продолжить эту работу и дополнил свою лунную теорию. Когда он ее завершил, у него было ни много ни мало семь «уравнений» лунного движения. Некоторые из них он получил не столько из фундаментальных гравитационных аргументов, сколько из наблюдений, произведенных Флемстидом. В лунных таблицах, основанных на его работе, использовались данные таких астрономов, как Флемстид, Чарльз Ледбетер и Галлей, но представляется сомнительным, что они были лучше таблиц, составленных на основе методов Хоррокса. Ньютон обладал превосходством с точки зрения потенциальных преимуществ – реальных достоинств, заложенных в его теории.

В 1690‐х гг. Ньютону срочно понадобились наблюдательные данные Флемстида, но эти два специалиста жестоко поссорились из‐за категорических разногласий в вопросе о роли теории – должна ли она направлять наблюдения или, наоборот, следовать им. Факт существования трений между Галлеем и Флемстидом создавал дополнительные сложности, однако стареющий Ньютон становился все более и более автократичным. Будучи смотрителем Монетного двора, он выделил щедрое пособие Галлею, использовав для этого службу финансового контроля Честерского монетного двора (1696). В 1699 г. положение дел резко обострилось, когда он сказал Флемстиду, что ему нужны только его наблюдения, а не расчеты. Флемстид всегда полагал, что его наблюдения, выполненные с помощью инструментов, приобретенных на его собственные средства, должны принадлежать только ему. Ньютон и Галлей придерживались мнения, что работа астронома Королевского общества была общей собственностью, и опубликовали в 1712 г. значительную часть его работы без получения его одобрения. Приход к власти в 1715 г. правительства Вигов привел к изменению конъюнктуры в пользу Флемстида. Через посредство лордов Казначейства он получил триста непроданных экземпляров изданной в 1712 г. «Historia coelestis». После удаления тех фрагментов, на которые он лично указал, сохранив несколько экземпляров для оправдания в глазах своих друзей, он с мрачным торжеством предал все остальное огню. По его словам, он «принес их в жертву небесной Истине». Флемстид долго готовил к публикации свою собственную работу – трехтомную «Historia coelestis Britannica». (В названии «Британская история небес» слово «история» употребляется в современном значении слова «данные».) Он умер в 1719 г., до того как она была подготовлена к печати, но в итоге книга увидела свет в 1725 г. Прилагающийся к ней звездный атлас (о нем мы еще будем говорить в главе 15) в 1729 г. опубликовали его вдова Маргарет и один из его ассистентов Джеймс Ходсон. Они благоразумно исключили раздел, подготовленный Флемстидом для того, чтобы выразить горькое сожаление по поводу своего сотрудничества с Ньютоном и Галлеем. Каталог и атлас Флемстида намного превосходили по точности все, что было издано до этого, но его репутация всегда находилась в тени репутации Ньютона.

В теории Луны Ньютона есть любопытная деталь, касающаяся оценки ее средней плотности по сравнению с плотностью Земли на основе относительных приливных воздействий Солнца и Луны. В первом издании «Principia» она была завышена в три раза. Факт кажущейся относительной легкости Земли дал основание Галлею сделать вывод о том, что она на четыре девятых полая. Он не был первым, кто подал такую идею, обнаруживаемую, например, в «Священной теории Земли» Томаса Бернета (1681, первое издание – на латыни), но у него можно найти нечто большее, чем просто старую традицию упоминания о гротах и пещерах, содержащуюся в древней мифологии. Галлей предпринял смелую попытку найти теорию земного магнетизма. Со времени путешествия на остров Святой Елены, которое он совершил в 1676 г., он изучал магнитное уклонение (угол расхождения между направлениями на истинный и магнитный север) и к 1683 г. пришел к выводу, что Земля обладает четырьмя магнитными полюсами. В то время он считал, что лучше всего это может быть объяснено с помощью гипотезы, согласно которой Земля состоит из внешней и внутренней сфер (не исключалась возможность, что этих сфер может быть несколько), вращающихся друг относительно друга и несущих собственные магнитные полюса. Существовало определенное сходство между этой гипотезой и более ранней моделью Земли, выдвинутой Гуком, но, как представляется, модель Галлея имела двойное обоснование и наряду с его работой о муссонах позволила ему занять почетное место в истории геофизики – науки, которая всегда поддерживала прочные связи с астрономией. Однако вскоре, когда ошибку Ньютона исправили, Земля перестала считаться полой. Портрет Галлея, написанный в 1736 г., когда он был Королевским астрономом, изображает его с полой Землей в руках. Современник Галлея Уильям Уистон широко пропагандировал эту идею в своей книге, вышедшей в 1717 г., и даже сопроводил ее библейскими свидетельствами, в которых упоминалось, что эта пустая полость обитаема.

«Principia» Ньютона часто характеризуют как самую важную работу из всех когда либо опубликованных в области физических наук. Критерии такого умозаключения сложно поддаются определению и могут сильно разниться, но саму эту работу безусловно можно рассматривать как нечто ознаменовавшее окончание одной исторической эпохи и начало другой. Она дала физическое обоснование описательным законам планетного движения Кеплера и, в этом смысле, легитимировала их или, как сказал сам Ньютон, превратила их из домыслов в факты. Кроме того, она предложила программу астрономических исследований, которая продолжается до сих пор (постоянно дополняясь и расширяясь). Его доказательства не всегда являлись полными; на деле, во многих случаях Ньютон еще не располагал хорошо разработанными математическими приемами, необходимыми для предоставления убедительного доказательства. Однако впоследствии астрономы с удивлением обнаружили, что он обладал удивительным инстинктом, позволяющим ему получать правильные решения, даже когда он прибегал к вынужденной маскировке нестыковок своей аргументации.

Сразу после первой публикации работу Ньютона встретили крайне враждебно по философским соображениям. Например, Лейбниц возражал против идей Ньютона об абсолютном пространстве и времени и «действии на расстоянии», относящихся, по его мнению, к мистическим категориям. В Англии было немало людей, которых тревожила мысль, что гравитация может воздействовать, проходя через пустое пространство, бесконтактно, и картезианские вихри имели большое количество приверженцев даже в этой стране. Декарт удерживал верховное правление на большей части континентальной Европы вплоть до смерти Ньютона. Лейбниц и Ньютон ожесточенно спорили по поводу приоритета на изобретение математического анализа. Когда обозленный Лейбниц начал (при посредстве принцессы Уэльской Каролины) обмениваться философскими размышлениями со сподвижником Ньютона Сэмюэлем Кларком, он не упускал случая высказать свои подозрения в том, что Ньютон и Кларк находятся в сговоре.

Лейбниц поднял вопрос, в котором сформулировал важный моральный принцип: должны ли мы отвергать физическую теорию как таковую, если есть все основания полагать, что она позволяет получать надежные результаты, но при этом является неблагонадежной с философской точки зрения. Этот вопрос никогда полностью не исчезал из философских дискуссий, но астрономы обычно всецело его игнорировали. Разве важно, что ньютоновская идея абсолютного пространства лишена логики? Получится ли у Лейбница или у его последователей представить в количественной форме семь неравенств Луны? Когда в астрономии начала XX в. в повестке дня появились доводы релятивистской теории, то зачастую признавалась их определенная связь с традицией, в которой рассуждал Лейбниц. Но если гораздо более важная связь с ньютоновской теорией упоминалась значительно реже, то это было только по следующей причине: она настолько вошла в плоть и кровь науки, что считалась само собой разумеющейся и привычной, как дедушкино пальто. И вряд ли будет правильно считать его донельзя изношенным даже в современных космологических масштабах.