Книга: Космос. Иллюстрированная история астрономии и космологии
Назад: ПОПЫТКИ СОЗДАНИЯ ФИЗИКИ ПЛАНЕТНОГО ДВИЖЕНИЯ
Дальше: ПЕРВЫЕ ТЕЛЕСКОПЫ: ОТОБРАЖЕНИЕ УВИДЕННОГО
КЕПЛЕРОВСКИЕ ЗАКОНЫ ПЛАНЕТНОГО ДВИЖЕНИЯ
Сила должна быть пропорциональна движению – так полагал Кеплер, как и многие до него. Сила вращения Солнца, приводящая в движение планеты, простирается вовне в трех измерениях таким образом, что величина ее воздействия должна уменьшаться пропорционально квадрату расстояния, однако Кеплеру никак не удавалось согласовать эту идею с известными ему скоростями планет. Что, если силы распространяются не в трех измерениях, а по каким-нибудь причинам ограничиваются плоскостью орбиты или непосредственно примыкающим к ней пространством? Может ли это привести к изменению скорости планет не пропорционально расстоянию? Для проверки этого предположения он формулирует свой вопрос, используя не скорости, а «задержки» – короткие интервалы времени, необходимые для покрытия малого участка дуги. Тогда, если задержка пропорциональна расстоянию этой малой дуги, то задержка большой дуги может быть получена суммированием всех расстояний находящихся на ней малых дуг. Способ разбиения орбиты на серии малых приращений дуги Кеплер почерпнул из архимедовой геометрической практики. Для суммирования расстояния по всему участку дуги для нахождения времени, затраченного планетой на ее покрытие, ему потребовалось выбрать сравнительно небольшой интервал дуги, но и это, по-видимому, привело его к бесконечно большому значению, а это абсурд. Область каждой секторальной компоненты, описываемая радиус-вектором, проведенным от Солнца, как он заметил, была примерно пропорциональна среднему расстоянию малой орбитальной дуги от Солнца, и значение этого приближения тем точнее, чем меньше дуга. Таким образом, общее время для сектора любого размера должно быть пропорционально его площади. Проделав все это, он получил то, что сегодня называется «законом площадей» или вторым законом планетного движения Кеплера. Выражаясь иначе: радиус-вектор, соединяющий Солнце с планетой, описывает одинаковые площади за одинаковые интервалы времени (ил. 143). По какой-то непонятной причине он не захотел вставить это пояснение в «Astronomia nova» и так и не нашел подходящего случая опубликовать этот закон в какой-либо из своих работ до выхода «Epitome».
142
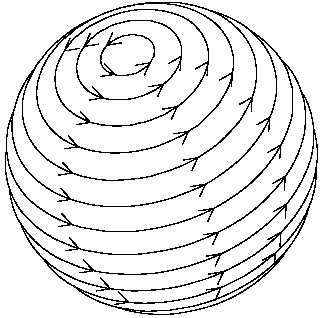
Расположение магнитных волокон, каким оно представлялось бы «взору» планеты, находящейся вне экваториальной плоскости Солнца. Согласно Кеплеру, эти волокна, являющиеся источником магнитной силы, нужны для того, чтобы толкать планеты с помощью солнечного вращения и поддерживать их изменяющееся расстояние до Солнца в правильном режиме посредством притяжения и отталкивания. Возникшая перед Кеплером невероятно сложная проблема магнетизма не помешала ему провести рассуждение в качественных категориях, согласно которому взаимное расположение волокон могло объяснить, почему все планеты расположены примерно в одной (эклиптической) плоскости.
Сам по себе закон площадей оказался недостаточен для устранения пресловутой ошибки в восемь минут дуги. Сначала, как это понятно сегодня, требовалось получить закон эллиптических орбит, однако это было не столь уж важно с точки зрения применяемой им исследовательской техники, и его гениальность проявилась в том числе в том, что он все же открыл этот закон, но чуть позже, а сделав это, положил конец доминированию кругов в планетной теории. Он установил закон площадей задолго до выхода в свет «Astronomia nova» и спустя какое-то время начал сомневаться в его справедливости, пока в итоге не был принужден заключить, что должен отказаться от предпосылки, согласно которой Марс обладает круговой орбитой. Он попытался использовать эпицикл с центром, выбранным таким образом, чтобы не нарушался закон площадей. Этого можно добиться, сделав деферент овальным, и он произвел огромное количество вычислений для самых разных овалов. Все зависело от точной формы орбиты, степени ее отклонения от правильного круга. Он знал: если бы это был эллипс, то в его распоряжении оказался бы хорошо изученный раздел геометрии – геометрия конических сечений Архимеда и Аполлония. На одном из этапов он использовал эллипс в качестве приближения к истинной орбите, очевидно, рассматривая его не более как средство, упрощающее расчет площадей. Однако создается впечатление, что на тот момент он искренне полагал, что удача отвернулась от него, коль скоро ему пришлось использовать для описания реальности столь несовершенную фигуру. К 1605 г., проделав многие сотни пробных вычислений и написав более пятидесяти глав уже завершенной «Astronomia nova», он все еще отводил эллипсу роль вспомогательного средства в своей теории. Он посвятил исследованию овалов целых десять глав своей книги, и каждый из них обязательно давал ошибку в октантах. В один момент он попытался увязать эллипс с магнитной гипотезой, но потерпел неудачу. Эллипс довольно хорошо описывал планетные направления, но плохо согласовывался с моделью флуктуирующих расстояний. Затем, через семь глав, он пришел к выводу, что эллипс способен удовлетворить обоим требованиям. Так возник первый закон Кеплера, как мы его сегодня называем: планета движется по эллиптической орбите с Солнцем в одном из фокусов этого эллипса. Потребовалось некоторое время на то, чтобы Кеплер смог приспособить закон площадей к эллипсу, но он сделал это еще до выхода «Epitome».
143
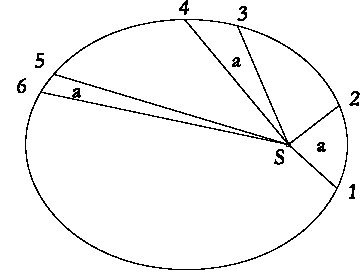
Второй закон движения планет Кеплера, «закон площадей». Равные площади (изображенные здесь в виде трех секторов, помеченных буквой a) заметаются за равные интервалы времени линией, соединяющей Солнце (S) с планетой. Позже Исаак Ньютон заметил, что его необходимо слегка подкорректировать, и в простейшей системе, состоящей из двух тел, точка S должна располагаться в центре масс Солнца и планеты.
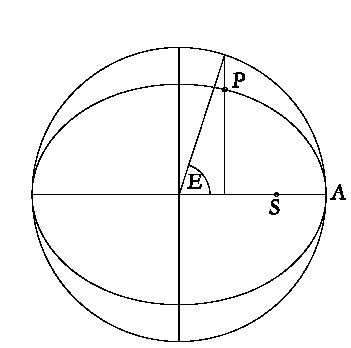
В ходе изложения своего подхода в «Epitome» Кеплер привел уравнение, само по себе способное претендовать на роль главного достижения решения задачи планетных орбит. Он пишет о нем как о следствии, полученном из физической теории отклонения магнитных волокон, что действительно могло иметь место, хотя ничто не мешало ему назвать следствием физической теории и эллиптическую орбиту. Следующее краткое пояснение «уравнения Кеплера» не столько объясняет его происхождение, сколько подчеркивает его важное значение для любого астронома – не только Кеплера, – желающего правильно рассчитать планетные положения. Уравнение связывает два угла, известные как эксцентрическая аномалия (E) и средняя аномалия (M). Первый угол показан на ил. 144, где точка P обозначает планету, S – Солнце, а A – перигелий, точку, в которой планета оказывается на наименьшем расстоянии от Солнца. Угол M не показан, но для тех, кто имеет навык аналитического мышления, он и не нужен. Это угол, описываемый радиус-вектором, движущимся с постоянной угловой скоростью. Мы можем переформулировать наше пояснение, осуществив переход к площадям, но не составит труда изобразить M как угол между SA и линией, исходящей из S, которая вращается с такой же средней скоростью, как планета, совпадая с ней при каждом прохождении через точку A. Далее, если e – это эксцентриситет эллипса, то уравнение Кеплера запишется в виде: E – esinE = M, если указанные углы записаны в радианах.
144
Диаграмма, иллюстрирующая соотношение, получившее название «уравнение Кеплера»
Очевидно, что угол M легко определяется, если известен угол E, но задача, стоящая перед вычислителем планетных положений, начинается с решения более общей проблемы: определения угла E по известному времени (или известному углу M, равномерно растущему с течением времени). Как впоследствии показали Ньютон и другие исследователи, это уравнение не имеет точного аналитического решения.
Применение различных аппроксимирующих приемов для решения указанного уравнения имеет долгую историю. Уже в IX в. Хабаш ал-Хасиб нашел приближенное решение аналогичной задачи, хотя и по другому поводу, тоже имеющему отношение к астрономии. До появления современных вычислительных методов, отодвинувших на второй план важность получения строгого аналитического решения этого уравнения, существовали особые таблицы, которые время от времени обновлялись и совершенствовались. Наиболее широко использовались таблицы Й. Ю. Астранда (1890) и Ю. Баушингера (1901), но Кеплер самостоятельно разработал довольно точные итерации и процедуры интерполяции для использования их в Рудольфовых таблицах.
Еще до завершения работы над таблицами ему посчастливилось познакомиться с логарифмами, изобретенными Джоном Непером (1614), о чем он узнал из работы, написанной другим автором. Оценив по достоинству принцип, лежащий в их основе, но не имея формул для их составления, он создал собственную таблицу логарифмов, но для других целей. Логарифмы сильно упрощали вычислительную работу, и с этого момента использование их в астрономии стало рутинным делом, пока спустя довольно долгое время их не начали заменять механическими калькуляторами (особенно с XIX в.). Практический аспект, связанный с необходимостью проведения вычислений, является обстоятельством, которое способно лишить теоретическую астрономию ее обаяния, и все же он, вне всякого сомнения, обладал громадной прикладной ценностью даже на стадии усовершенствования теории; Кеплер был из тех, кто первым подписался бы под этим утверждением. Надо отметить, что обычно логарифмы составлялись для чисел, выраженных в десятичной системе, в то время как астрономы традиционно выражали углы в шестидесятеричной системе. Спустя некоторое время, не все это знают, были составлены огромные тома логарифмов для шестидесятеричных чисел, оказавшиеся особенно полезными в морской навигации, использующей астрономические методы.
Рудольфовы таблицы оказались гораздо надежнее всего сделанного в этой области ранее. Например, прежде ошибка для Марса могла достигать 5°, теперь же она не превышала тринадцатой доли этого значения. Кеплер впервые в истории сумел точно предсказать время прохождения Меркурия и Венеры по диску Солнца. Он умер в 1630 г., за год до того как можно было увидеть эту необычную пару прохождений, но предсказанное им прохождение Меркурия сумели пронаблюдать Пьер Гассенди в Париже, Иоганн Баптист Цизат в Ингольштадте и Ремус Квиетанус в Руффахе. (Прохождение Венеры для территории Европы было недоступно.)
Как мы убедились, астрономия Кеплера основывалась на физике и геометрии. При всем уважении к натуральной философии, его никогда не покидала страсть к геометрическим гармониям. Как мы уже видели, несмотря на то что «Harmonice mundi» выросла из стиля его научного мышления в молодые годы, он не публиковал ее до 1619 г. Ко времени, когда она вышла в свет, он сосредоточил внимание на поиске гармоний, которые могут быть присущи планетным скоростям, если смотреть на них со стороны Солнца. В духе своего раннего отношения к Земле, способной воспринимать планетные аспекты, он писал теперь, что Солнцу тоже может быть присуща некая разновидность зрения или осмысленного ощущения, обладающего возможностью воспринимать угловые смещения планет и гармонию их движения. Он находился в поиске новых типов гармонии – как для отдельных, так и для соседствующих планет, вовлекая в постижение гармоний, обнаруживаемых планетными эксцентриситетами, Божественное Провидение. (Он был не первым, кто применил такой подход. В 1531 г. Филипп Меланхтон написал предисловие к новому изданию «Сакробоско», которое приобрело известность в силу широкого использования в университетах в качестве основополагающего текста. Меланхтон писал о траекториях и законах планет с целью помочь человечеству достичь познания Бога и Божественного Провидения.) Кеплер почти закончил писать «Harmonice mundi», когда наткнулся на то, что сегодня называют его «третьим законом». Согласно этому закону период планеты пропорционален длине большой полуоси ее эллиптической орбиты, возведенной в степень 3/2. (Последнее расстояние является средним расстоянием планеты от Солнца. Для круговой орбиты это просто радиус.) В этой работе он изложил указанный закон почти не снабдив его комментариями, а предложенное им доказательство было опубликовано только во второй части «Epitome». В своем объяснении он попытался количественно интерпретировать идею зрительных оболочек Солнца, ответственных за подталкивание планеты вдоль круговой траектории, и магнитную материю самой планеты, количество которой зависело от ее объема. Это ad hoc объяснение, очевидно, не являлось той тропинкой, что привела его к этому открытию.
Третий закон, как признавал сам Кеплер, крайне важен, поскольку он позволял определять относительные размеры двух орбит с помощью довольно простого сравнения их периодов. Общей единицей для измерения этих расстояний является большая полуось земной орбиты (а. е. или астрономическая единица), и, конечно же, общей единицей для измерения времени является земной период, а именно один год. В качестве примера: сидерический период Марса легко определяется как 1,881 (тропического) года, и поэтому, согласно третьему закону Кеплера, его среднее расстояние от Солнца равно 1,881, возведенному в степень 2/3, то есть 1,523 астрономической единицы. Ньютон показал в своих «Principia», что этот закон может быть выведен из гравитационного закона обратных квадратов, который, таким образом, может рассматриваться как подтверждение эмпирического закона Кеплера. В действительности, как было указано ранее, принимая во внимание ускорение, сообщаемое Солнцу планетой, законы Ньютона требовали внесения небольших изменений в закон Кеплера. Поскольку даже самая массивная планета (Юпитер) составляет менее тысячной доли массы Солнца, эта поправка крайне незначительна, и зачастую третий закон Кеплера до сих пор рассматривается как точный.
Кеплер видел в себе не только астронома в привычном смысле этого слова. Он желал постичь гармонию Вселенной, используя для этого в высшей степени индивидуализированное сочетание математики, физики, философии и чистого мистицизма. Все лучшие астрономы, пошедшие по его стопам, не решились перенять его амбициозный стиль, но в итоге разобрались с тем, как можно использовать его законы для целей вычисления – тех самых целей, ради достижения которых его нанял Тихо. Тяжкое бремя расчета Рудольфовых таблиц было для него и горем, и усладой, наряду с параллельными изысканиями в объяснении крайне сложного движения Луны. Таблицы представляли собой не сами эфемериды, а (как и большинство их предыдущих аналогов) инструмент расчета отдельных положений или эфемерид. Получаемые с их помощью положения были во много раз точнее всего, что имелось до этого; прежняя ошибка в несколько градусов не превышала в некоторых случаях нескольких угловых минут. Кеплер надеялся использовать Рудольфовы таблицы для возмещения невыплаченного жалованья, но их печатание прервалось вторжением в Линц войск Контрреформации. Ему и его лютеранским издателям разрешили остаться, и лишь в 1627 г., когда Кеплер сумел устроиться в Ульме, печатание его таблиц, наконец, завершилось. С учетом того факта, что в его жизнь постоянно вторгались перипетии религиозных войн, легко понять полет фантазии, который уносил его от всей этой суматохи, когда он раз за разом возвращался к своему «Somnium seu astronomia lunari» («Сон, или лунная астрономия»), начатому в 1609 г. Эту научно-фантастическую историю о путешествии на Луну он использовал как литературный прием (в русле традиции, заданной Цицероном) для отстаивания коперниканского порядка расположения планет, что было предельно очевидно для наблюдателя, находящегося на Луне. В итоге ее опубликовал в 1634 г. его зять Якоб Барч. К моменту смерти Кеплера государство, которому он служил бо́льшую часть своей жизни, осталось должно ему более 12 000 гульденов.

