Text tagging algorithms

The process of text tagging can be explained by the following figure:

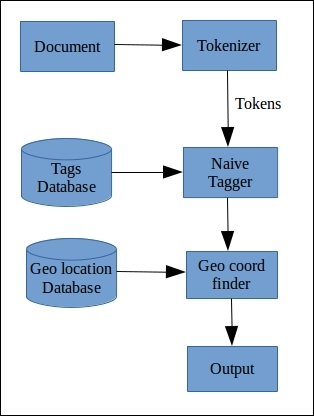
A document is tokenized and the tokens are passed to the naive tagger. The naive tagger uses a tagging algorithm to find the tags. Then, the geo-coordinate finder identifies the geo-locations (lat-long coordinates) corresponding to those tags. They are then available as the output.

There are various text tagging algorithms, each of which has its own benefits. Let us go through some of the algorithms that can be used for text tagging.

Fuzzy string matching algorithm

The fuzzy string matching algorithm can be used to match two strings, exactly or partially. This means the relationship is fuzzy when there is a set of n-elements and another set of m-elements, and both partially match the same elements. Using this algorithm, we can identify strings that are similar to a set of other strings. It is like drawing similar terms from the string.

Suppose we want to find the similarity between two words, say jumps and juumpss, and correct them if necessary. The fuzzy string matching algorithm will return true for the first word (jumps) as it is correct and will return the correct string (jumps) for the other word juumpss.

The fuzzy string matching algorithm is characterized by a metric that is a function of the distance between two words. This helps us evaluate the similarity between them. This metric is known as edit distance.

Edit distance is defined as the number of operations required to transform one string to another. Using edit distance, we can quantify the dissimilarity between two strings. Edit distance can be used as an NLP mechanism to find corrections for a misspelled word. This is done by identifying words from a dictionary that have the smallest edit distance with respect to the word for which corrections are sought.

Let us see an example to calculate the edit distance. We will find the number of primitive operations, insertions, deletion, and substitution, that are required to convert a string to obtain an exact match with another. This number will be the edit distance between the string and the pattern:

Mak can be converted to Make by an insertion operation:
```
    Mak + e = Make
```
Boooks can be converted to Books by a deletion operation:
```
    Boooks - o = Books
```
Dish can be converted to Fish by a substitution operation:
```
    Dish + (- D + F) = Fish
```

The edit distance between these examples is numerically 1, as only a single operation is required to convert them to the target string.

Let us look at some algorithms used for calculating the edit distance.

The Levenshtein distance algorithm

Levenshtein distance is defined as the minimum number of single-character edits required to convert one word to another. Here the edits are performed by insertion, deletion, and substitution operations that we saw earlier.

Sitting can be converted to Bettings by the following operation:

    Sitting + (- S + B) = Bitting     Bitting + (- i + e) = Betting     Betting + s = Bettings

In the previous example, the Levenshtein distance between Sitting and Bettings is 3 (2 substitution operations + 1 insertion operation).

If the lengths of the two strings are m and n, the algorithm will have a time complexity of O(mn) and a space complexity of O(mn). In addition, the Levenshtein distance has the following properties:

It is at least the difference of the sizes of the two strings
It is at most the length of the longer string
The distance is 0 if both strings are equal
The distance is equal to the number of substitutions required for conversion (hamming distance) if both strings are of the same size

Damerau–Levenshtein distance

The Damerau–Levenshtein algorithm is an extension of the Levenshtein distance algorithm. It involves an additional operation, transposition. Transposition is the operation whereby the adjacent characters are swapped in order to bring them to a certain form. Let us see an example of transposition:

The word eat can be converted to ate by two transposition operations:
```
    eat => aet (swap e & a)     aet => ate (swap e & t)
```

Therefore, the Damerau–Levenshtein algorithm consists of four operations:

Insertion
Deletion
Substitution
Transposition

Let us look at an example for calculating the Damerau–Levenshtein distance:

The word clocks can be converted to bold formatting by the following operation:

    clocks => substitute c with b => blocks     blocks => transpose l and o => bolcks     bolcks => substitute c with d => boldks     boldks => substitute k with e => boldes     boldes => substitute s with r => bolder

The Damerau–Levenshtein distance in this example is 5 (1 transpose + 4 substitution).