ГЛАВА 24
ДИЗАЙН МЕХАНИЗМОВ
Институты создаются для изменения человеческого поведения. Для того чтобы они сохраняли эффективность с течением времени, их необходимо адаптировать к изменениям в окружающей среде или обществе, которое они призваны регулировать.
Дженна Беднар
В этой главе мы покажем, как использовать модели для разработки политических и экономических институтов. Институт включает инструменты для обмена информацией, а также процедуры принятия решений, перераспределения ресурсов или получения требуемых результатов на основе имеющейся информации. На рынках люди обмениваются информацией посредством цен для заключения торговых сделок и принятия производственных решений. В иерархических системах они взаимодействуют с помощью письменного языка с целью организации выполнения рабочих планов, а в демократических странах сообщают о своих предпочтениях путем голосования. При этом правила голосования определяют политику. Тщательно разработанные институты стимулируют коммуникации и действия, которые обеспечивают требуемый результат. Неэффективные институты этого не делают.
В главе представлена концептуальная схема моделирования институтов, известная как дизайн механизмов. В ней выделяется четырем аспекта реальных институтов: информация (то, что участники знают и должны сообщить); стимулы (выгоды и издержки совершения определенных действий); агрегирование (то, как индивидуальные действия трансформируются в коллективный результат); вычислительная сложность (когнитивные требования, предъявляемые к участникам).
Истоки дизайна механизмов восходят к анализу общих вопросов, связанных с распределением благ, в частности вопроса о том, обеспечивают ли рыночные механизмы или централизованное планирование их оптимальное распределение. Первые модели исходили из поведенческих правил, таких как принятие установившихся на рынке цен или правдивое голосование. Затем автор модели анализировал последствия таких линий поведения, например, как они агрегируются. Со временем от такого подхода отказались в пользу подхода, учитывающего оптимизирующее поведение, что сделало эти конструкции поддающимися объяснению с точки зрения теории игр. Далее специалисты по дизайну механизмов находят равновесия Нэша и сравнивают институты с учетом рационального поведения.
Данная концептуальная схема доказала свою полезность. Ее можно использовать для поиска недостатков в действующих правилах и процедурах, чтобы объяснить, почему те или иные институты преуспевают или терпят неудачу, а также для прогнозирования результатов. С ее помощью разработано множество институтов, в том числе аукционы частот, о которых шла речь в , а также много других торговых интернет-площадок, государственных систем голосования и даже процедур выделения пространства для проектов на космических кораблях многоразового использования .
В представленном в главе анализе шесть частей. Сначала мы опишем концептуальную схему дизайна механизмов с помощью диаграммы Маунта-Рейтера. Затем рассмотрим задачу с участием трех человек, выбирающих из двух альтернатив. В третьей части проанализируем три механизма проведения аукционов и обнаружим, что все они дают одинаковые результаты. В четвертой покажем, что это не случайное совпадение, и опишем фундаментальный результат — теорему об эквивалентности доходов, которая доказывает, что любой механизм проведения аукциона, удовлетворяющий определенным исходным предположениям, обеспечивает один и тот же исход. В пятой части мы сравним механизм голосования по правилу большинства голосов с механизмом опорных точек как способами принятия решений о целесообразности реализации того или иного общественного проекта. И в заключение расширим обсуждение механизмов с учетом критики равновесий Нэша.
ДИАГРАММА МАУНТА-РАЙТЕРА
Механизм состоит из шести частей: среда (соответствующие свойства мира); набор исходов; набор действий (называемый пространством сообщений); правило поведения, которого придерживаются люди, чтобы произвести действие; функция исхода, которая устанавливает соответствие между действиями и исходами, а также соответствие общественного выбора, ставящее среду в соответствие со множеством желаемых исходов. Соответствие общественного выбора обычно включает либо исход, максимизирующий сумму значений полезности участников, либо множество Парето-эффективных распределений. Исход эффективен по Парето тогда и только тогда, когда не существует другого результата, которому бы все отдавали предпочтение. Эффективность по Парето — это нижний предел.
Эффективность по Парето
В пределах множества исходов тот или иной исход является доминируемым по Парето при наличии альтернативы, которой все отдают предпочтение. Все остальные исходы эффективны по Парето .
Диаграмма Маунта-Райтера отображает все эти важные элементы механизма графически (рис. 24.1), сопоставляя то, что нам нужно, с тем, что у нас есть. В ее верхней части соответствие общественного выбора описывает исходы, к которым мы обычно стремимся. В нижней части отображен адаптированный вариант реальности. Люди применяют правила поведения для передачи сообщений или выполнения действий. Функция исхода устанавливает соответствие между этими действиями и результатами. В идеале нижний, более сложный путь, обеспечивает тот же результат, что и верхний путь, то есть желаемый исход.
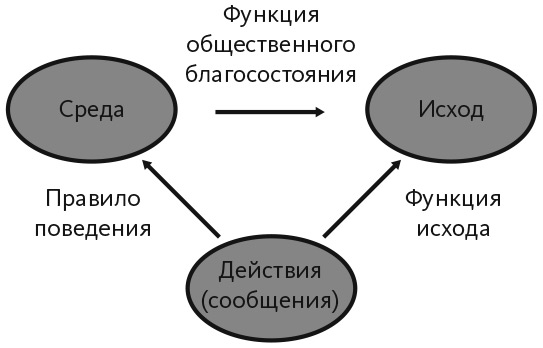
Рис. 24.1. Диаграмма Маунта-Райтера
Однако не все механизмы эффективны. Например, если среда включает людей с определенными предпочтениями в отношении какого-то общественного блага, соответствие общественного выбора сопоставляет их предпочтения с оптимальным уровнем этого блага. Но, как мы видели в , механизм добровольных взносов, согласно которому люди платят за определенную долю общественного блага столько, сколько пожелают, приводит к тому, что каждый человек обеспечивает 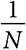 единиц общественного блага, а не оптимальное количество — N единиц. Когда исход, порождаемый определенным механизмом, не согласуется с нашими целями, мы говорим, что этот механизм не обеспечивает соответствия общественного выбора.
единиц общественного блага, а не оптимальное количество — N единиц. Когда исход, порождаемый определенным механизмом, не согласуется с нашими целями, мы говорим, что этот механизм не обеспечивает соответствия общественного выбора.
Список свойств, которым должен удовлетворять механизм, зависит от контекста. Мы опишем пять таких свойств. Во-первых, равновесный исход, полученный с помощью механизма, должен согласовываться с принципом соответствия общественного выбора (эффективность по Парето). Во-вторых, в идеале участники должны применять доминирующие стратегии, то есть их действия не должны зависеть от действий остальных. Если это так, мы говорим, что эффективный исход достижим с помощью доминирующей стратегии. В-третьих, механизм должен быть таким, чтобы не нужно было принуждать людей в нем участвовать (добровольное участие). В-четвертых, если механизм подразумевает передачу или оплату ресурсов, необходимо, чтобы не приходилось вкладывать дополнительные средства или истощать ресурсы (сбалансированность бюджета). Далее в ходе анализа механизмов принятия решений по общественно значимым проектам мы увидим, что удовлетворить эти условия непросто. И наконец, в-пятых, во многих случаях требуется раскрытие истины. Сообщения, которые отправляют люди, должны раскрывать их истинную информацию или истинный тип. Специалисты по теории игр называют это совместимостью по стимулам. В большинстве значимых случаев ни один механизм не может удовлетворять всем условиям. Таким образом, одно из важных достижений дизайна механизмов — демонстрация пределов возможного.
ПРИНЦИП БОЛЬШИНСТВА И МЕХАНИЗМ «СОЗДАТЕЛЬ КОРОЛЕЙ»
Первый тип рассматриваемой нами среды включает людей, голосующих за совершение совместного действия или принятие законопроекта. Мы возьмем трех человек (назовем их Ума, Вера и Уилл), которые хотят вместе посмотреть фильм и должны решить, что это будет — боевик, драма или комедия. Эта же среда применима к трем военным, решающим, атаковать ли противника, оборонять свои позиции или отступать. В любой интерпретации среда состоит из трех человек с предпочтениями по трем альтернативам. Запишем эти предпочтения в виде упорядоченного списка. Порядок предпочтений «боевик > комедия > драма» говорит о том, что наибольшее предпочтение отдается боевику, далее следует комедия, а затем драма. Мы будем исходить из следующих порядков предпочтений:
Ума: боевик > комедия > драма
Вера: комедия > драма > боевик
Уилл: комедия > драма > боевик
В этом примере мы представим соответствие общественного выбора как множество Парето-эффективных вариантов выбора. С учетом предполагаемых предпочтений комедия и боевик являются эффективными по Парето, а драма — доминируемой по Парето по отношению к комедии.
Сначала оценим в качестве механизма принцип большинства. В случае равного разделения голосов будем исходить из того, что выбор делается в случайном порядке. Если люди голосуют честно, то комедия получает два голоса. Однако допустим, что и Вера, и Уилл думают, что голоса двоих оставшихся распределятся между драмой и боевиком и что каждый проголосует за драму. Предположим также, что голосование проходит по очереди. Вера голосует первой и выбирает драму. Уилл голосует вторым и делает то же самое. Голос Умы уже не важен, но допустим, что во избежание конфликта она тоже голосует за драму. Эти три голоса образуют равновесие Нэша. Ни у кого нет стимула менять свой голос. В данном случае принцип большинства не всегда приводит к Парето-эффективному исходу.
Теперь рассмотрим механизм «Создатель королей» . В соответствии с ним одного человека в случайном порядке выбирают «создателем королей». Затем он назначает «короля», который и определяет выбор группы. Если создателем короля будет Уилл, то он должен выбрать между Умой и Верой. Кого бы он ни выбрал, этот человек становится королем и выбирает фильм.
Если выбранный в качестве короля человек действует рационально, то он выберет свой любимый фильм. Следовательно, такой исход будет эффективным по Парето. В силу этого механизм создателя королей обеспечивает получение Парето-эффективных исходов. Дополнительное преимущество этого механизма состоит в том, что если у любых двух человек один и тот же любимый фильм, то он будет выбран независимо от того, кого Уилл назначит королем. Так произойдет, если Ума и Вера предпочитают один и тот же фильм. Однако если Уиллу и Уме нравится один и тот же фильм, то Уиллу нужно выбрать Уму.
ТРИ ТИПА АУКЦИОНОВ
Теперь, получив базовое представление о механизмах, приступим к изучению аукционов. Большинство из нас немного знакомы с аукционами ввиду широкого распространения таких интернет-площадок, как eBay. Аукционы используются и в других ситуациях, в том числе при заключении государственных контрактов, на рынках подержанных автомобилей и в большинстве случаев размещения интернет-рекламы. Мы сосредоточимся на аукционах с участием одного продавца и множества участников торгов. В качестве предмета торгов может выступать дом, автомобиль, билеты на футбольный матч или произведения искусства. Предположим также, что каждый участник торгов устанавливает предмету торгов уникальную оценочную стоимость, чтобы исключить равенство результатов. Тогда Парето-эффективным исходом будет такой исход, при котором предмет торгов достается участнику с самой высокой оценочной стоимостью. Любой другой исход будет Парето-доминируемым по отношению к этому исходу. Теперь сравним три типа аукционов: аукцион с повышением цены, аукцион первой цены и аукцион второй цены.
АУКЦИОНЫ С ПОВЫШЕНИЕМ ЦЕНЫ
В ходе аукциона с повышением цены аукционист называет цену. Любой участник торгов, готовый ее заплатить, поднимает руку. Аукционист повышает цену до тех пор, пока не останется один участник; он затем платит цену, на которой предпоследний участник опустил руку. В случае аукциона с повышением цены рациональный участник торгов участвует в аукционе до тех пор, пока цена не достигнет его оценочной стоимости. Если он выйдет раньше, то может не получить предмета торгов по хорошей цене. Если же он продолжит участие в аукционе после того, как цена превысит его оценочную стоимость, то может получить предмет торгов, но заплатит за него больше оценочной стоимости, что в итоге даст чистый убыток.
Когда все участники торгов действуют рационально, участник с самой высокой оценочной стоимостью получает предмет торгов и платит за него цену, равную оценочной стоимости участника, предложившего вторую по величине цену. В качестве примера предположим, что есть три участника торгов с оценочной стоимостью 30, 60 и 80 долларов. Когда цена, названная аукционистом, превышает 30 долларов, первый участник торгов выходит из аукциона. Когда цена достигает 60 долларов, аукцион покидает второй участник. В результате третий участник выигрывает аукцион и платит 60 долларов .
В случае аукциона второй цены участник торгов подает заявку в запечатанном конверте. Остальные участники торгов не видят предложенной им цены. Предмет торгов достается участнику, предложившему максимальную цену, но он заплатит сумму, равную второй по величине предложенной цене. Схема проведения аукциона второй цены делает предоставление правдивой информации оптимальным. Представьте, что участник, оценивший предмет торгов в 80 долларов, решает, как предложить цену на аукционе второй цены. Предположим, что другие участники торгов уже подали свои заявки. Наш участник торгов должен проанализировать три возможных случая: самая высокая цена остальных участников может быть меньше 80 долларов, равна 80 долларам или больше 80 долларов. В каждом из этих случаев участник торгов получит лучший результат, сообщив свою истинную оценочную стоимость предмета торгов.
Логика становится понятнее, если рассмотреть ее на примере. Будем исходить из того, что установленная участником торгов оценочная стоимость предмета составляет 80 долларов. Рассмотрим четыре варианта самых высоких цен, предложенных другими участниками: 70 долларов (ниже), 80 долларов (столько же), 82 доллара (немного выше) или 90 долларов (выше). В табл. 24.1 показаны выигрыши для различных предложений цены в диапазоне от 65 долларов до 95 долларов.
Таблица 24.1. Чистый выигрыш в зависимости от различных предложений цены при оценочной стоимости 80 долларов
| Самая высокая цена | Участник с оценочной стоимостью 80 | |||
| 65 | 80 | 85 | 95 | |
| 70 (низкая) | 0 | +10 | +10 | +10 |
| 80 (равная) | 0 | 0 | 0 | 0 |
| 82 (немного выше) | 0 | 0 | −2 | −2 |
| 90 (высокая) | 0 | 0 | 0 | −10 |
Как следует из таблицы, предложение цены 80 всегда обеспечивает как минимум такой же высокий выигрыш, как и любое другое предложение. Подача заявки с указанием истинной оценочной стоимости — всегда наилучшее действие (доминирующая стратегия). Аналогичная логика применима ко всем участникам торгов, поэтому все должны предлагать цену, соответствующую истинной оценочной стоимости (данный механизм совместим по стимулам). Из этого следует, что в случае аукциона второй цены участник торгов с самой высокой оценочной стоимостью выигрывает аукцион и платит сумму, равную оценочной стоимости участника торгов, предложившего вторую по величине цену.
На аукционе первой цены каждый участник торгов предлагают свою цену, предложение с самой высокой ценой побеждает, а участник торгов, сделавший его, платит сумму, равную этой цене. Как и на аукционе второй цены, заявки подаются одновременно, поэтому никто не знает цен других участников торгов. Оптимальная стратегия предложения цены в ходе аукциона первой цены зависит от мнения участника торгов относительно оценочной стоимости (а значит, и вероятных предложений цены) других участников. Мы будем считать, что участники торгов не знают оценочной стоимости других участников, но имеют правильное представление о распределении оценок. Точнее говоря, будем исходить из того, что оценки участников торгов равномерно распределены в диапазоне от нуля до 100 долларов и что всем участникам торгов известно об этом распределении. Кроме того, каждый участник торгов знает, что эта информация известна всем остальным участникам.
С помощью математики мы можем продемонстрировать, что если оценки равномерно распределены и все участники торгов придерживаются оптимальной стратегии предложения цены, то при наличии двух участников торгов каждый должен предложить цену, равную половине его истинной оценочной стоимости, а при наличии N участников каждый должен предложить цену, равную 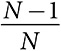 от его истинной оценочной стоимости. Следовательно, участник аукциона с еще девятнадцатью участниками должен предложить цену, составляющую 95 процентов от его истинной оценочной стоимости. При использовании этого правила торгов предмет торга всегда выигрывает участник с самой высокой оценочной стоимостью. Мы можем также показать, что сумма, которую он заплатит, эквивалентна ожидаемой стоимости участника, предложившего вторую по величине цену. Таким образом, аукцион с повышением цены также обеспечивает эффективный исход, а цена соответствует ожидаемой стоимости участника торгов, предложившего вторую по величине цену .
от его истинной оценочной стоимости. Следовательно, участник аукциона с еще девятнадцатью участниками должен предложить цену, составляющую 95 процентов от его истинной оценочной стоимости. При использовании этого правила торгов предмет торга всегда выигрывает участник с самой высокой оценочной стоимостью. Мы можем также показать, что сумма, которую он заплатит, эквивалентна ожидаемой стоимости участника, предложившего вторую по величине цену. Таким образом, аукцион с повышением цены также обеспечивает эффективный исход, а цена соответствует ожидаемой стоимости участника торгов, предложившего вторую по величине цену .
До описания данной модели многие из нас пришли бы к выводу, что чем больше участников в аукционе, тем выше цену должен предлагать каждый из них. Но без математических расчетов мы не знали бы равновесного правила предложения цены. Модель предоставляет нам точное выражение для определения цены, которую должен предлагать покупатель. Эта сумма увеличивается в соответствии с оценочной стоимостью участника торгов, а это подразумевает, что участник с самой высокой оценочной стоимостью выиграет аукцион, точно так же как и в случае аукционов двух других типов.
ТЕОРЕМА ОБ ЭКВИВАЛЕНТНОСТИ ДОХОДОВ
В каждом из трех форматов аукционов выигрывает участник с самой высокой оценочной стоимостью. Следовательно, все три механизма гарантируют эффективный исход. Кроме того, ожидаемая сумма, уплаченная победителем аукциона, равна оценочной стоимости участника торгов, предложившего вторую по величине цену. Иначе говоря, все три аукциона обеспечивают одинаковый ожидаемый доход, а предмет торгов достается одному и тому же покупателю. Это просто удивительно. Но еще удивительнее возможность доказать тот факт, что победитель и ожидаемая оценочная стоимость остаются одними и теми же для любого аукциона, где участники придерживаются оптимальной стратегии предложения цены, предмет торгов при этом достается участнику, предложившему самую высокую цену, а участник с нулевой оценочной стоимостью не получает выигрыша. Другими словами, аукционы, удовлетворяющие этим условиям, обеспечивают один и тот же ожидаемый результат, известный как теорема об эквивалентности доходов .
Теорема об эквивалентности доходов
Любой аукцион, участники которого выбирают независимые частные оценки стоимости из известного общего распределения, обеспечивает один и тот же доход продавцу и одинаковые ожидаемые выигрыши покупателям, если каждый участник торгов делает предложение о покупке, максимизирующее его ожидаемый выигрыш; при этом участник торгов, предлагающий самую высокую цену, всегда получает предмет торгов, а участник торгов с нулевой оценкой стоимости имеет нулевой выигрыш.
Теорема об эквивалентности доходов подразумевает, что аукцион «платят все» (в ходе которого каждый участник, даже проигравший, платит сумму своего предложения) обеспечивает тот же исход, что и аукцион второй цены . Даже такой необычный формат, как аукцион третьей цены (в ходе которого выигрывает участник, предложивший самую высокую цену, и платит сумму, равную третьей по величине цене), дает того же победителя и тот же доход. Теорема об эквивалентности доходов не означает, что правила проведения аукционов не важны. Во время реальных торгов участники могут не применять оптимальных стратегий или, как в случае аукциона первой цены, по-разному представлять себе распределение оценок других участников. При выполнении любого из этих условий (участники торгов не придерживаются оптимальной стратегии или имеют разные представления о распределении оценок) доход может варьироваться в зависимости от типа аукциона. Эмпирические и экспериментальные испытания действительно выявляют определенные различия в том, какие результаты обеспечивают аукционы.
Итак, чем больше ставки и искушеннее участники торгов, тем выше вероятность, что люди будут действовать рационально. В ходе интернет-аукционов по продаже потребительских товаров некоторые люди могут придерживаться эмпирических правил или исходить из предубеждений (например, предлагать цену с шагом 10 долларов). Но на многомиллионном аукционе по аренде нефтеносных участков участники торгов, скорее всего, имеют доступ ко всей необходимой информации и соответствующий опыт.
Кроме того, тип аукциона может влиять на количество участников торгов. Например, аукционы первой цены по продаже древесины привлекают больше мелких участников торгов, чем аукционы с повышением цены, поскольку у мелких участников есть хотя бы какой-то шанс выиграть, если более крупные участники предлагают низкие цены. В случае аукциона с повышением цены у мелких участников торгов нет никаких шансов, так как более крупные компании видят их предложения и называют более высокую цену .
Аукционы также отличаются когнитивными требованиями, предъявляемыми к участникам. В случае некоторых аукционов научиться оптимальному поведению не сложно. В ходе аукциона с повышением цены участник торгов должен участвовать в аукционе, пока цена не достигнет его оценочной стоимости. Действия других участников, не придерживающихся оптимальной стратегии, могут привести к повышению или снижению ожидаемого выигрыша участника торгов, но они не меняют оптимальной стратегии: участник торгов должен участвовать в аукционе до тех пор, пока цена меньше его оценочной стоимости. Аналогично, в ходе аукциона второй цены участник торгов должен всегда придерживаться одной и той же стратегии — предлагать цену, соответствующую его истинной оценочной стоимости. Тем не менее для того, чтобы прийти к выводу об оптимальности правдивого предложения цены, понадобится выполнить несколько шагов логических рассуждений.
Напомним, что доминирующие стратегии являются оптимальными независимо от стратегий других участников аукциона. И аукционы с повышением цены, и аукционы второй цены имеют доминирующие стратегии. У аукциона первой цены такой стратегии нет. В аукционе первой цены изменения в стратегии предложения цены одного участника торгов могут изменить оптимальную стратегию другого участника. Если один участник торгов всегда предлагает либо ноль, либо 50, то другой участник должен всегда предлагать либо 1, либо 51. Нет никаких причин предлагать 60 или 70, поскольку тогда победителю придется переплатить за предмет торгов. Учитывая поведение другого участника, если предложение 60 может выиграть аукцион, то же может сделать и предложение 51.
Даже если у аукциона есть доминирующая стратегия, не все доминирующие стратегии одинаково легко вычислить. Для аукциона с повышением цены стратегия (участие в аукционе до тех пор, пока цена меньше оценочной стоимости участника торгов) требует одного шага логических рассуждений: если цена меньше оценки, покупать по этой цене. В случае аукциона второй цены участник торгов должен проанализировать несколько вариантов развития событий, чтобы понять, что раскрытие правдивой информации — оптимальная стратегия. Безусловно, после участия в нескольких аукционах второй цены он будет знать это точно.
И последняя особенность аукционов, требующая рассмотрения, — поощряет ли аукцион неоптимальное поведение. На аукционы первой и второй цены участники торгов подают заявки, не зная, какую цену предлагают другие участники. На аукционе с повышением цены участники торгов видят, как повышается цена, и знают, кто продолжает участвовать в торгах. Иногда это приводит к тому, что участник торгов переоценивает значимость победы в аукционе и повышает цену. Аукционисты на благотворительных аукционах пытаются поднять ставки путем эмоциональных призывов — например, показывая видео с детьми, резвящимися на новой детской площадке, которая будет построена за счет предложенных ставок.
Успех стратегий зависит от эмоций участников торгов. Трудно представить, чтобы на аукционах по продаже древесины убеждали участников торгов предлагать больше их прогнозных оценок. Но гораздо легче представить участника благотворительного аукциона, который предлагает более высокую цену, поскольку эти деньги пойдут на благое дело. Изменят ли участники торгов свои оценки в процессе проведения торгов, можно только догадываться. Нам просто нужно признать, что это может произойти. В ходе аукционов первой и второй цены участники торгов делают одно предложение, что не оставляет шансов для эмоциональных призывов во время аукциона.
И наконец, на аукционе первой цены и аукционе с повышением цены цена равна самому высокому предложению, а в случае аукциона второй цены — второй по величине цене. Это создает впечатление, что продавец мог бы получить более высокую цену, а также отчасти объясняет, почему правительства не используют аукционы второй цены. Только представьте заголовки газет в случае, если бы правительство получило три заявки на получение прав на добычу нефти — на 6, 8 и 12 миллионов долларов: «Правительство получает заявку на 12 миллионов долларов, но продает землю за 8 миллионов долларов». Любой, кто знает теорию аукционов, понял бы, что если бы правительство провело аукцион первой цены или аукцион с повышением цен, максимальная предложенная цена составляла бы не 12, а 8 миллионов долларов.
Как уже неоднократно подчеркивалось в книге, формальные модели раскрывают условия, необходимые для обеспечения требуемого результата. Теорема об эквивалентности доходов не говорит о том, что все механизмы проведения аукционов обеспечивают один и тот же исход. Она гласит, что все аукционы, в которых участники придерживаются оптимальной стратегии, предмет торгов достается участнику, предложившему самую высокую цену, а участник торгов с нулевой оценкой стоимости получает нулевой выигрыш, эквивалентны. Продавец может собрать больше денег, ослабив одно из этих трех предположений. Однако продавцу будет трудно заставить людей действовать вопреки собственным интересам и уж тем более вряд ли удастся получить деньги от человека, для которого данный товар не представляет ценности. Остается только один вариант — не продавать предмет торгов покупателю, предложившему самую высокую цену. Один из способов сделать это — вообще не продавать товар. Если продавцу известно распределение оценок, он может установить низшую отправную цену, минимальную ставку. При определенных условиях это может повысить его ожидаемый доход. Предположим, продавец уверен, что три участника оценивают предмет торгов в 5, 10 и 60. Воспользовавшись любым из описанных выше аукционов, победитель предложит цену 60 долларов, а заплатит 10 долларов. Продавец может получить более высокий доход, установив низшую отправную цену 60 долларов и проведя аукцион первой цены.
МЕХАНИЗМЫ ПРИНЯТИЯ РЕШЕНИЙ ПО ОБЩЕСТВЕННЫМ ПРОЕКТАМ
Далее мы сравним два механизма принятия решений о целесообразности реализации таких общественных проектов, как строительство школы, новой автомагистрали или спортивной арены. И при этом будем исходить из того, что проект имеет для каждого человека индивидуальную ценность и что его реализация влечет за собой коллективные затраты.
Задача принятия решения по общественному проекту
Пусть (V1, V2, …, VN) обозначает денежную оценку полезности, которую N человек приписывают общественному проекту стоимостью C. Проект целесообразно осуществлять тогда и только тогда, когда C < V1 + V2 + … + VN.
Сначала рассмотрим механизм равного участия в расходах при принятии решения о реализации проекта большинством голосов. В соответствии с этим механизмом люди голосуют за целесообразность реализации проекта. Если большинство голосует «за», расходы на реализацию проекта делятся поровну между участниками голосования.
Механизм равного участия при принятии решения большинством голосов
Люди голосуют за или против реализации проекта. Если большинство голосует за проект, он реализуется, и каждый участник голосования платит сумму 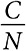 . Как следует из представленного ниже примера, этот механизм может нарушать условие эффективности и добровольного участия.
. Как следует из представленного ниже примера, этот механизм может нарушать условие эффективности и добровольного участия.
Из пространственной модели голосования мы знаем, что реализация проекта зависит от предпочтений медианного избирателя. В данном случае это будет человек с медианным значением ценности, которую представляет для него общественный проект. В силу своей структуры этот механизм удовлетворяет условию сбалансированности бюджета и условию совместимости по стимулам, но вместе с тем он не всегда удовлетворяет условиям эффективности или добровольного участия, как видно из следующего примера. Предположим, три человека оценивают общественный проект стоимостью 300 долларов в 0, 120 и 150 долларов. Эффективный исход состоит в том, что проект не следует реализовывать, поскольку его общая стоимость 300 долларов превышает сумму индивидуальных оценок. Тем не менее, ввиду того что затраты на проект будут разделены поровну, каждый решает, стоит ли осуществлять проект при затратах 100 долларов на человека. Из этого следует, что за проект проголосуют два из трех человек, и он будет реализован, но это неэффективный исход. Более того, выигрыш человека, оценившего проект в 0 долларов, составляет −100 долларов, а значит, пример также демонстрирует нарушение условия о добровольном участии.
В соответствии со вторым механизмом под названием «механизм поворота» каждый человек сообщает свою оценку проекта. Если сумма оценок превышает стоимость проекта, принимается решение о его реализации. В противном случае проект не поддерживается. Сумма, которую должен внести человек на реализацию проекта, равна разности между стоимостью проекта и суммой оценок всех остальных участников голосования. Если их оценки превышают стоимость проекта, этот человек ничего не платит.
Механизм поворота
Человек i сообщает оценку 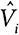 проекта стоимостью C. Если сумма индивидуальных оценок превышает эту стоимость, то проект реализуется.
проекта стоимостью C. Если сумма индивидуальных оценок превышает эту стоимость, то проект реализуется.
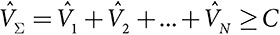 .
.
Человек i не делает взноса, если 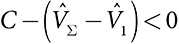 , и делает взнос
, и делает взнос 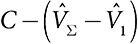 в противном случае. Этот механизм совместим по стимулам
в противном случае. Этот механизм совместим по стимулам 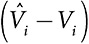 , эффективен и индивидуально рационален. Как показывает представленный ниже пример, он может нарушать условие сбалансированности бюджета.
, эффективен и индивидуально рационален. Как показывает представленный ниже пример, он может нарушать условие сбалансированности бюджета.
Пример: (V1, V2, V3) = (60, 120, 150) и C = 300
Проект целесообразно реализовать ввиду того, что 300 < 60 + 120 + 150.
Человек 1 делает взнос 30 долларов, что равно разности между стоимостью проекта и суммой других оценок (300 – 270); человек 2 вносит 90 долларов; а человек 3 — 120 долларов. Общая сумма взносов составляет 240, что меньше стоимости проекта.
Согласно логике, аналогичной логике аукциона второй цены, этот механизм удовлетворяет условию совместимости по стимулам. Предположим, стоимость проекта составляет 300 долларов, а человек оценивает его в 80 долларов. Существует три варианта развития событий. Если другие оценки дают в сумме меньше 220 долларов, у человека нет стимула сообщать оценку выше 80 долларов, поскольку ему придется заплатить эту сумму. Однако если сумма оценок других людей превышает 300 долларов, то он ничего не платит и может вообще не предоставлять свою оценку. Но если сумма оценок других людей составляет от 220 долларов до 300 долларов, то, сообщив оценку 80, человек заплатит разность между 300 долларами и этой суммой, и проект будет реализован (эффективный исход). Этому человеку не хотелось бы сообщать оценку, скажем, 70 долларов, поскольку сумма других оценок могла бы быть меньше 225 долларов, и его низкая оценка помешала бы реализовать проект. Если бы он предложил оценку 80 долларов, проект был бы реализован и обошелся бы ему всего в 75 долларов.
Так как механизм поворота удовлетворяет условию совместимости по стимулам, он также удовлетворяет и условию эффективности. Проект реализуется только в случае, если сумма оценок превышает его стоимость. Обратите внимание, что поскольку сообщение истинной оценки — это доминирующая стратегия, эффективный исход осуществим тоже с помощью доминирующей стратегии. Кроме того, учитывая, что каждый человек делает взнос, не превышающий его оценку проекта, механизм удовлетворяет условию добровольного участия.
В задаче принятия решений по общественным проектам ни один механизм не удовлетворяет всем необходимым критериям. Тот факт, что мы можем использовать модели для доказательства этого вывода, способен сэкономить нам массу времени, которое мы бы потратили на попытки реализовать невозможное. Подобно тому как инженеры не тратят время зря на попытки изобрести вечный двигатель, специалисты по дизайну механизмов не стремятся к созданию совместимых по стимулам, индивидуально рациональных, эффективных, обеспечивающих сбалансированность бюджета механизмов для решения проблем по общественным проектам. Таких механизмов не существует.
Механизм поворота удовлетворяет почти всем условиям, кроме сбалансированности бюджета. Эта проблема не решается путем повышения суммы взносов людей на реализацию проекта, поскольку это сделало бы механизм несовместимым по стимулам и не индивидуально рациональным. У людей появился бы стимул лгать, а некоторым предложили бы внести больше, чем их оценка полезности проекта. Один из возможных вариантов выхода из ситуации — собрать деньги каким-то иным способом и сформировать резерв денежных средств, доступных для реализации проектов. Это само по себе создаст проблемы стимулирования, хотя и не напрямую. Более эффективное решение — найти другой источник финансирования. Например, университет, имеющий как крупный центральный фонд пожертвований, так и отдельные фонды колледжей, мог бы использовать этот механизм, чтобы решить, стоит ли строить новый студенческий клуб. У декана каждого колледжа был бы стимул сообщить свою истинную оценку полезности такого клуба, а ректор университета мог бы восполнить недостающую сумму. Компания, состоящая из отдельных подразделений с бюджетными полномочиями, могла бы сделать то же самое. Решение относительно проекта перехода на облачную систему тоже можно было бы принять с помощью механизма поворота, а любую нехватку средств покрыло бы высшее руководство.
РЕЗЮМЕ
Концептуальная схема дизайна механизмов позволяет сравнивать механизмы по ряду критериев. Обеспечивает ли механизм эффективные результаты? Говорят ли люди правду? Станут ли они добровольно участвовать? Порождает ли механизм бюджетный излишек или убыток? Концептуальная схема дизайна механизмов позволяет определить, каких результатов можно достичь. Порой удовлетворить все необходимые критерии в рамках одного механизма не удается. В таких случаях создатели моделей становятся инженерами. Мы используем модели, чтобы попытаться сконструировать действенные решения.
По мере изменения технологий могут меняться и механизмы. Возьмем, к примеру, аукционы, используемые такими поисковиками, как Google. Первоначально в Google взимали фиксированную плату за тысячу кликов. Этот механизм оказался неоптимальным ввиду изменений в области информационных технологий, которые позволили Google одновременно проводить миллионы аукционов. Благодаря аукционам компания Google увеличила доход и стала более эффективно распределять места для рекламы. В настоящее время Google использует обобщенный аукцион второй цены. Каждый участник торгов предлагает плату за переход по ссылке для рекламы ключевого слова, скажем «мезотелиома» (онкологическое заболевание, вызванное воздействием асбеста). Участник торгов, предложивший самую высокую цену, получает первый рекламный блок; участник, предложивший вторую по величине цену, — второй рекламный блок, а участник, предложивший третью по величине цену, — третий рекламный блок. Цены, которые они заплатят, определяются так же, как и в случае аукциона второй цены.
Предположим, четыре предложения с максимальными ценами составляют 10, 7, 6 и 3 доллара за клик. Участник торгов, предложивший третью по величине цену, заплатит сумму, равную четвертому по величине предложению, 3 доллара. Участник торгов, предложивший вторую по величине цену, заплатит сумму, равную третьему по величине предложению, 6 долларов. А участник торгов, предложивший самую высокую цену, заплатит 7 долларов . Выяснив оценки рекламодателей, в Google могли бы установить низшую отправную цену и получить еще больше денег. Однако такой исход вряд ли наступил бы, если бы участники торгов знали о плане Google. Участник торгов, полагающий, что именно он предложит самую высокую цену, не хотел бы, чтобы в Google знали его оценку. Кроме того, установление низшей отправной цены навредило бы репутации Google, поскольку было бы воспринято как отказ Google от сотрудничества: Google не может претендовать на ту или иную низшую отправную ценность для мест на веб-странице. Верхний рекламный блок на странице поиска по ключевым словам практически не имеет для Google ценности до тех пор, пока не будет продан. Однако это не относится к продажам винтажных альбомов или подержанных автомобилей, так как эти товары имеют ценность сами по себе, поэтому здесь низшая отправная цена оправданна. Заботясь о своей репутации, в Google не склонны устанавливать минимальную отправную цену в погоне за максимальной прибылью, ведь это наверняка разгневает рекламодателей.
Таким образом, модели дизайна механизмов помогают разрабатывать и выбирать институты, а также позволяют определить, что можно и нельзя реализовать на практике. В частности, невозможно разработать механизм, который обеспечивает эффективный исход, стимулирует людей говорить правду и позволяет сбалансировать бюджет. Поэтому не стоит тратить время и усилия на попытки достичь невозможного. Лучше направить энергию на поиск компромисса между эффективностью, раскрытием истины и сбалансированным бюджетом.
Дизайн механизмов можно также использовать для изучения более масштабных вопросов, например, когда следует использовать рынок, когда нужно голосовать, когда целесообразнее положиться на иерархический механизм и когда лучше прибегнуть к помощи добровольного коллектива, чтобы распределить ресурс или принять решение относительно тех или иных действий . Каждый из этих четырех институтов (рынки, демократии, иерархии и коллективы) эффективно функционирует в одних условиях и менее эффективно в других. Например, не нужно голосовать за то, какие товары должны покупать люди, и не следует использовать рынки для выбора политических лидеров.
В рамках организации и общества в целом можно увидеть каждую из этих институциональных форм. Университет имеет дело с рынком профессоров, опирается на демократию при найме преподавателей, зачисляет на курсы обучения посредством иерархии и разрабатывает стратегические планы с помощью коллективов. Некоммерческие, коммерческие и правительственные организации также представляют собой сочетание этих институциональных форм. Инструменты дизайна механизмов позволяют формально сравнить, как функционируют эти институты, и оптимально распределить между ними задачи.

