ГЛАВА 21
ТРИ КЛАССА МОДЕЛЕЙ ТЕОРИИ ИГР
Дедуктивное умозаключение движется от абстрактного к конкретному. Оно начинается с набора аксиом и использует законы логики и математики, для того чтобы посредством манипуляций с ними формировать прогнозы в отношении окружающего мира.
Рейчел Кросон
Теория игр моделирует стратегические взаимодействия. Многие из описанных ниже моделей, в том числе модели кооперации, сигнализирования, механизмов и коллективных действий, включают игры. Мы не будем особо углубляться в анализ игр, потому что этой теме посвящено множество отдельных книг, а просто дадим общее представление о теории игр. Для этого рассмотрим три основных класса игр: игры в нормальной форме, в которых игроки выбирают из дискретного набора действий (как правило, двух); последовательные игры, в которых игроки выбирают действия последовательно; и игры непрерывного действия, в которых игроки выбирают действия любого масштаба или с эффектом любой величины. Эти примеры вводят основные понятия, помогают осмыслить модели, представленные ниже, и сами по себе добавляют ценность.
Глава состоит из четырех частей. В первой рассказывается об играх с нулевой суммой. В такой игре каждый из двух игроков выбирает одно из двух действий. Какие бы действия ни выбрали игроки, выигрыш одного игрока эквивалентен проигрышу другого. Мы используем игры с нулевой суммой, чтобы дать определение основных терминов теории игр, провести различие между стратегиями и действиями и ввести понятие итеративного удаления доминируемых стратегий. Затем мы проанализируем последовательную игру «Выход на рынок», в которой потенциальный игрок рынка конкурирует с действующей компанией. Многократное повторение игры порождает так называемый парадокс сети магазинов. В третьей части мы рассмотрим игру усилий, в которой игроки выбирают уровень усилий, которые они готовы приложить, чтобы выиграть фиксированную сумму. Активизация усилий повышает шансы игрока получить приз. Глава завершается кратким обсуждением ценности моделей теории игр в целом.
ИГРЫ С НУЛЕВОЙ СУММОЙ В НОРМАЛЬНОЙ ФОРМЕ
В этом разделе мы проанализируем две игры с нулевой суммой в нормальной форме с участием двух игроков. В обеих играх каждый игрок выбирает действие и получает выигрыш, который зависит от его собственных действий и от действий другого игрока. Кроме того, сумма выигрышей игроков равна нулю. В первой игре под названием «Орел — решка» (рис. 21.1) каждый игрок выбирает одно из двух действий: орел или решка. Игроку, которому соответствует строка матрицы (назовем его игрок строки), выбирает то же действие, что и другой игрок, а игрок, которому соответствует столбец матрицы (назовем его игрок столбца), выбирает другое действие.
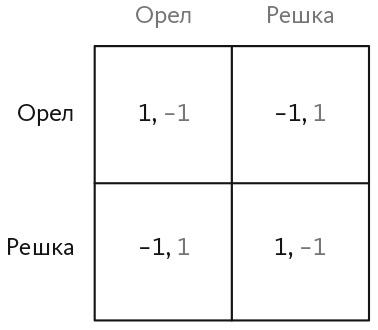
Рис. 21.1. Игра «Орел — решка»
Стратегия — это правило ведения игры. Это может быть выбор одного действия, случайный выбор между действиями или, как мы увидим в следующем разделе, последовательность действий. Равновесие Нэша в игре — это пара стратегий, подобранных таким образом, что стратегия каждого игрока оптимальна с учетом стратегии другого игрока. В игре «Орел — решка» в случае уникальной равновесной стратегии оба игрока в равной степени делают случайный выбор между двумя действиями. Для того чтобы доказать, что рандомизация обеспечивает равновесие, необходимо показать, что если один игрок делает случайный выбор, то другому тоже лучше его сделать. Продемонстрировать это не составит труда. Если игрок строки (действия и выигрыши которого выделены жирным шрифтом) выбирает орла с вероятностью 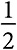 и решку с вероятностью
и решку с вероятностью 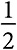 , то выигрыш игрока столбца будет равен нулю независимо от его действий. Следовательно, рандомизация — это оптимальная стратегия для игрока столбца. В силу симметрии рандомизация будет оптимальной стратегией и для игрока строки.
, то выигрыш игрока столбца будет равен нулю независимо от его действий. Следовательно, рандомизация — это оптимальная стратегия для игрока столбца. В силу симметрии рандомизация будет оптимальной стратегией и для игрока строки.
Такая оптимальность рандомизации влияет на поведение в стратегических ситуациях. Спорт — это игра с нулевой суммой: одна команда (или игрок) выигрывает, а другая проигрывает. Выполняя пенальти, нападающий пытается в случайном порядке выбирать, куда целиться — в правый или левый угол ворот. В теннисе подающему игроку необходимо в случайном порядке подавать мяч в пределах или за пределы корта. В американском футболе в ситуации «четвертый и гол» команде нападения нужно случайным образом сделать выбор между пробежкой и пасом. В каждом из этих случаев соперник также стремится рандомизировать запланированные ответные действия. Любое неслучайное действие может быть использовано. Это верно и для карточных игр, таких как покер. Хороший игрок в покер блефует в случайном порядке. Если бы он блефовал всегда, соперники разгадали бы его стратегию и остались бы в игре. Тогда игрок проигрывал бы каждый раз, блефуя. Аналогично, если бы игрок никогда не блефовал, его соперники научились бы сбрасывать карты. Оптимальный блеф заставляет противников колебаться, решая, оставаться им в игре или сбросить карты.
На рис. 21.2 показана вторая игра, игра с минимизацией риска. В ней каждый игрок может предпринять рискованное либо безопасное действие. Это асимметричная игра с нулевой суммой. Выигрыши зависят не только от действий, но и от того, какой игрок совершает какое действие. В этой игре доминирующая стратегия игрока строки — не рисковать. Независимо от того, какое действие выберет игрок столбца, игрок строки получает более высокий выигрыш, выбирая безопасное действие. У игрока столбца нет доминирующей стратегии. Если игрок строки выбирает рискованное действие, игрок столбца тоже должен выбрать рискованное действие. Если игрок строки выбирает безопасное действие, то и игрок столбца должен его выбрать.
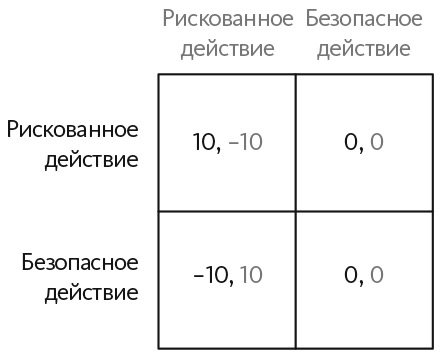
Рис. 21.2. Игра с минимизацией риска
Проанализировав стимулы игрока строки, игрок столбца может сделать вывод, что игрок строки никогда не выберет рискованное действие, поскольку безопасное действие предпочтительнее рискованного. Следовательно, игрок столбца знает, что игрок строки выберет безопасное действие. С учетом этого факта он тоже должен выбрать безопасное действие. Такой тип логических рассуждений, в соответствии с которым один игрок исключает доминируемые (преобладающие) стратегии другого, известен как итеративное удаление доминируемых стратегий. В этой игре использование итеративного удаления доминируемых стратегий показывает, что выбор безопасного действия обоими игроками и есть уникальное равновесие Нэша.
ПОСЛЕДОВАТЕЛЬНЫЕ ИГРЫ
В последовательной игре игроки выполняют действия в определенном порядке, как показано на дереве игры, состоящем из узлов и ветвей. Каждый узел соответствует тому моменту, когда игрок должен совершить действие. Каждая ветвь, исходящая из этого узла, обозначает одно из возможных действий. У концевых ветвей дерева игры записывается выигрыш в случае выбора соответствующей цепочки действий. На рис. 21.3 представлено дерево игры «Выход на рынок».
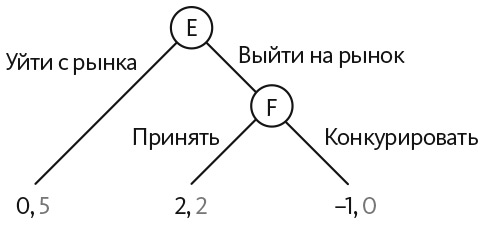
Рис. 21.3. Игра «Выход на рынок»
В игре «Выход на рынок» два участника — потенциальный игрок рынка и действующая компания. Если потенциальный игрок решает не выходить на рынок (левая ветвь дерева), он не получает никакого выигрыша, а действующая компания получает выигрыш 5. Если потенциальный игрок выходит на рынок, действующая компания должна выбирать — принять его, что повлечет за собой снижение прибыли с 5 до 2, или конкурировать с ним, сведя свою прибыль до нуля, а нового игрока рынка — до отрицательной. Мы будем считать, что прибыль нового игрока рынка должна быть отрицательной, поскольку он вынужден оплатить стоимость выхода на рынок.
В последовательной игре стратегия соответствует выбору действия в каждом узле. Предположим, действующая компания решает конкурировать, если потенциальный игрок выйдет на рынок. Зная об этом, потенциальный игрок решает этого не делать, так как это приведет к отрицательной прибыли. Такая совокупность действий — потенциальный игрок решает не выходить на рынок, а действующая компания планирует вести конкурентную борьбу, если он все же передумает, — представляет собой равновесие Нэша, но это не единственное равновесие и не наиболее вероятный исход игры. Существует еще одно равновесие, в котором потенциальный игрок решает выйти на рынок, а действующая компания принимает этот ход и не вступает в конкуренцию.
Для того чтобы выбрать одно из двух равновесий, требуется применить уточняющий критерий. В последовательных играх наиболее распространенный уточняющий критерий позволяет выбрать совершенное под-игровое равновесие. Его можно найти с помощью метода обратной индукции: начиная с концевых узлов выбирать оптимальное действие в каждом узле, а затем пройти дерево игры в обратном порядке, предполагая, что каждый игрок выбирает наилучшее действие с учетом действий другого игрока в последующих узлах. В игре «Выход на рынок» следует начать с концевого узла действующей компании. У нее оптимальное действие — принять. Перемещаясь далее вверх по дереву, мы увидим, что оптимальная стратегия потенциального игрока — выйти на рынок.
Игра становится еще интереснее в случае повторения. Представьте, что компания присутствует на многих рынках. Это может быть торговая сеть с франшизными магазинами в десятках городов. Допустим также, что существует ряд потенциальных игроков рынка. Тогда компания будет разыгрывать одну игру «Выход на рынок» за другой.
Применив метод обратной индукции и начав с последнего рынка, действующая компания примет нового игрока рынка, поскольку это действие максимизирует выигрыш. Следуя той же логике, компания примет предпоследнего нового игрока рынка, так же как и всех остальных. Таким образом, в данной последовательности игр уникальное совершенное равновесие под-игры состоит в том, что все потенциальные игроки решают выйти на рынок, и действующая компания принимает их всех.
Хотя выход на рынок и принятие нового игрока рынка — это уникальное совершенное под-игровое равновесие, в действительности так бывает не всегда. Представьте, что мы — члены совета директоров действующей компании и сталкиваемся с первым потенциальным игроком, который (изучив теорию игр) выходит на рынок. У нас может возникнуть желание вступить с ним в конкурентную борьбу, чтобы предотвратить выход новых игроков на другие рынки. Конкуренцию можно считать разумной стратегией, если она достоверна, то есть если мы можем создать репутацию компании, готовой конкурировать. В таком случае исход игры, к которому мы стремимся, отличается от совершенного равновесия под-игры.
Разрыв между тем, что прогнозирует теория игр, и тем, чего пытаются добиться реальные игроки, специалисты по теории игр называют парадоксом сети магазинов. Это один из примеров, когда поведение, которое теория игр считает оптимальным, может не совпадать с поведением, выбираемым опытным игроком в случае высоких ставок. Этот пример не опровергает теорию игр и не подрывает предположение о рациональном выборе, но показывает, почему мы должны всегда ставить предположения под сомнение.
ИГРЫ НЕПРЕРЫВНОГО ДЕЙСТВИЯ
Теперь давайте рассмотрим игру, участники которой выбирают из непрерывного множества возможных действий. В ней действия соответствуют уровням усилий. Выбирая более высокий уровень усилий, игрок повышает вероятность получить приз. Игра позволяет смоделировать любое количество игроков.
Выражение, описывающее равновесные усилия, раскрывает ряд важных моментов. Как и следовало ожидать, уровень индивидуальных усилий игрока повышается вместе с увеличением размера приза. Кроме того, при равновесии общий уровень усилий будет ниже стоимости приза. Это тоже вполне ожидаемо, учитывая, что игроки выбирают оптимальные действия. Игроки должны прилагать усилия, чтобы выиграть, но в разумных пределах.
Игра усилий
Каждый из N игроков выбирает уровень усилий (который можно представить в денежном выражении), чтобы выиграть приз стоимостью M. Вероятность того, что игрок выиграет приз, равна частному от уровня его усилий и общего уровня усилий всех игроков. Если Ei — уровень усилий игрока i, его вероятность выиграть приз можно описать следующим уравнением :
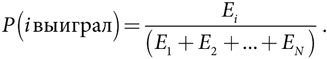
Равновесие:
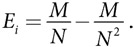
Мы можем увидеть воздействие увеличения количества игроков на уровень индивидуальных и общих усилий. Здесь выводы менее интуитивно понятны. Согласно этой модели, уровень усилий отдельных игроков снижается, а суммарный уровень усилий всех игроков повышается. Следовательно, модель подразумевает, что попытки организаторов всевозможных конкурсов привлечь больше участников, как ни парадоксально, могут привести к снижению качества победителей, поскольку у участников более крупных конкурсов будет меньше стимулов прилагать дополнительные усилия.
РЕЗЮМЕ
Мы начали главу с рассмотрения игры с нулевой суммой. Такие игры подразумевают полное отсутствие взаимовыгодных комбинаций действий. Любое действие, выигрышное для одного игрока, неизбежно будет проигрышным для другого. В решении с нулевой суммой любое действие наносит кому-то вред в такой же степени, в какой приносит другому пользу. Многие личные действия и выбор курса действий — это действия с нулевой суммой как минимум по одному из аспектов. У каждого из нас есть определенное количество часов в сутках, денег на расходы и ресурсов, которые можно на что-то выделить. Вместе с тем действие с нулевой суммой по одному аспекту может не быть действием с нулевой суммой по другому аспекту. Перераспределение бюджета может быть действием с нулевой суммой с финансовой точки зрения, но с положительной или отрицательной суммой с точки зрения счастья или самореализации людей.
В каждом конкретном случае мы всегда должны анализировать, порождает ли предложенное изменение игру с нулевой суммой. Например, многие люди выступают за выбор школы, в которую будет ходить их ребенок, поскольку это усиливает конкуренцию. Рыночная логика говорит о том, что когда школы вынуждены конкурировать, у них появляется стимул к повышению качества обучения.
Однако такой стимул имеет место только при наличии избыточного предложения образовательных услуг. В противном случае выбор школы может создать игру с нулевой суммой среди учеников. Представьте себе город с 10 000 учеников и 10 школами, рассчитанными на 1000 учеников каждая. Если ученики ранжируют эти школы в одном и том же порядке, места в лучших школах придется распределять с помощью лотереи. Тот, кто ее выиграет, будет ходить в лучшую школу. Проигравшим достанутся худшие школы, которые будут продолжать работать ввиду отсутствия избыточного предложения. Ученики играют в игру с нулевой суммой. Если откроется новая школа или имеющаяся повысит качество обучения, эта игра перестанет быть с нулевой суммой. В таком случае выиграть могут все.
Как рыночная модель, так и модель с нулевой суммой позволяют глубже понять происходящее. Рыночная модель раскрывает стимулы к повышению качества обучения и созданию новых школ. Модель с нулевой суммой показывает, что просто выбор школы означает, что одни ученики выиграют, а другие проиграют. Относительная значимость, которую нам следует присвоить каждой модели, зависит от контекста: существует ли избыток мощностей в лучших школах, чтобы они могли принять дополнительных учеников? Есть ли у школ ресурсы и знания для повышения качества обучения? Построят ли предприниматели новые школы? Позволяет ли транспортная система без проблем добираться до разных школ, чтобы между ними могла возникнуть конкуренция?
Из всего этого можно сделать вывод, что ни одна из двух моделей не дает правильного ответа, но каждая позволяет получить полезную информацию. Выбор школы действительно создает конкуренцию. Перевесят ли положительные аспекты конкуренции такой отрицательный аспект, как затраты на распределение учеников, зависит от контекста. Для того чтобы выбрать правильный курс действий, необходимо упорядочить совокупность моделей на множестве фактов.
Проблема идентификации
Данные о действиях людей часто указывают на кластерное поведение. Хорошие студенты с большей вероятностью дружат с другими хорошими студентами, а не с отстающими. Люди, которые занимаются преступной деятельностью, чаще сотрудничают с себе подобными преступниками, чем с добропорядочными гражданами. Многие положительные и отрицательные аспекты социальной жизни (такие как курение, физическое состояние, ожирение и даже счастье) образуют кластеры в социальных сетях. Кроме того, люди объединяются в кластеры по убеждениям — демократы, республиканцы или либертарианцы.
У нас есть два типа моделей, объясняющих кластеризацию: модели эффекта окружения и модели сортировки. Первые объясняют кластеризацию с помощью теории игр. Люди играют в координационную игру со своими друзьями. В моделях сортировки люди перемещаются ближе к себе подобным. Кластер хороших студентов может сформироваться либо в результате координации ими своих действий на основе общей модели поведения (эффект окружения), либо потому, что хорошие студенты предпочитают общаться друг с другом (сортировка). На основании мгновенного снимка данных эти два исхода неотличимы.
Данные. Студенты получают либо высокие (H), либо средние (M) баллы, которые в равной степени вероятны. Студенты образуют дружеские группы численностью 4 человека со следующим распределением:
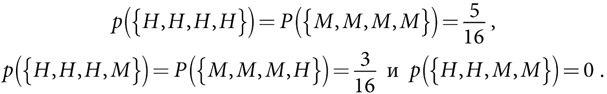
Модель эффекта окружения. Сначала студенты формируют произвольные группы из четырех человек:
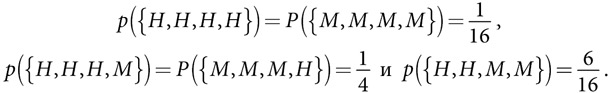
Тип студентов, принадлежащих к группам, состоящим только из одного типа людей, не меняется. Человек, тип которого отличается от остальных, меняет его, в результате чего группа {H, H, H, M} становится группой {H, H, H, H}. В группах с равным количеством студентов каждого типа один член группы меняет свой тип. Группа {H, H, M, M} может с равной вероятностью стать и группой {H, H, H, M}, и группой {M, M, M, H}.
Модель сортировки. Сначала студенты образуют произвольные группы из четырех человек. В любой группе с двумя типами студент, тип которого противоположен типу как минимум двух других людей, меняется группами с кем-то, имеющим другой тип. Из этого следует, что группа {H, H, H, M} становится группой {H, H, H, H}, а группа {M, M, M, H} — группой {M, M, M, M}, а также что любая группа вида {H, H, M, M} может с равной вероятностью стать группой {H, H, H, M} или {M, M, M, H}.
Обе модели согласуются с данными, что создает проблему идентификации. На основании только снимка данных мы не можем определить, относится ли курение, чтение манги (японских комиксов) или катание на лонгбордах к модели эффекта окружения или к модели сортировки. Иногда можно установить, какая модель применима. Склонность людей на Среднем Западе говорить «шипучка», а на побережьях — «содовая» позволяет смело предположить, что ими движет эффект окружения — мало кто переезжает в Бостон, чтобы называть кока-колу «содовой». Более важные аспекты поведения, такие как академическая успеваемость, употребление наркотиков, ожирение и счастье, требуют временных рядов данных, чтобы выяснить, какая из моделей применима. Анализ данных за определенный период помогает определить, меняют ли люди свое поведение, чтобы соответствовать друзьям (эффект окружения), или меняют друзей и сохраняют поведение (сортировка). Во многих значимых случаях, таких как успеваемость в школе, могут наблюдаться оба эффекта .

