Глава 7. Многопользовательская игра

Стрелок, преступник и шериф встретились на городской площади. Пролетело перекати-поле. Они потянулись к своим револьверам.

У стрелка была доля секунды, чтобы решить, кого застрелить – преступника или шерифа. У него не было времени рассмотреть, куда целится каждый из них, – может быть слишком поздно. Он должен решить сейчас. Но кого выбрать?

Ему заплатили за выстрел в шерифа. Так он и должен сделать.

Но постойте. Шериф знал, что стрелку заплатили, чтобы тот убил его. Следовательно, шериф выстрелит в стрелка в целях самообороны, что позволит преступнику свободно стрелять в того, кого он хочет. А у преступника было желание кровавой мести против стрелка, потому что стрелок шесть месяцев назад украл у него лошадь. Так что преступник, вероятно, тоже будет стрелять в стрелка. И стрелок знал, что преступник стреляет намного лучше, чем шериф. Поэтому, чтобы защитить себя, он выбрал преступника и надеялся, что шериф промахнется.

Шериф все это знал, а также знал, что стрелок попытается сначала остановить преступника. Тогда у шерифа будет возможность стрелять, в кого он захочет. Следовательно, он бы выстрелил в преступника, потому что это была его работа и еще потому, что не хотел, чтобы его уличили в драке с преступником, который стреляет лучше.

Но преступник знал об этом. И стрелок знал, что он это знает. И шериф знал, что они оба знают что-то еще. Стрелок снова и снова прокручивал в голове все эти схемы, в то время как его рука крепко сжимала пистолет.

Теория игр

Теория игр – это область математики, которая анализирует взаимодействие между движениями и контрдвижениями в многопользовательских играх. Несмотря на название, геймдизайнеры часто игнорируют теорию игр, потому что она кажется слишком абстрактной для реального мира. Хотя нам и не нужно вычислять точные цифры, как это делают математики, основы теории игр освещают ключевые концепции многопользовательского геймдизайна.

Теория игр помогает анализировать ситуации, когда игроки должны предвидеть и реагировать на решения друг друга.

Подумайте о разнице между разрушением заброшенного замка и нападением на захваченный замок.

Разрушение пустого замка – задача из области физики. Возможно, придется подобрать лучшее место для установки подъемного механизма или лучший способ убрать завалы камней. Но при том, что эти задачи могут быть сложными, пустой замок не вспоминает о вас, он просто следует законам физики. Это похоже на однопользовательскую игру, так как разум одного игрока сталкивается с механической системой.

Разрушение замка с обороняющимися – совершенно другая история. Теперь есть два умных мозга, которые пытаются превзойти друг друга. Обороняющийся генерал заранее просчитает ваши шаги и нанесет ответный удар. Он откинет лестницы, выстрелит огнем по тарану и пошлет наемных убийц, чтобы убить вашего генерала. И будет прогнозировать ваши ответные ходы. Он будет посылать ложные сигналы, чтобы заманить вас в ловушку или попытаться скрыть слабые места в стене. Теория игр описывает взаимодействие между вашим разумом и разумом соперника.

Представьте, что однажды ночью во время осады вы выбираете стратегию на следующий день. Вы выбираете между атакой ворот тараном и подрывом стены саперами, а обороняющийся выбирает между горючей смолой, которую можно вылить сверху, и лучниками, которые будут стрелять в ваших саперов. Вы оба должны выбрать один вариант, и, поскольку готовиться нужно ночью, вы не будете знать, какой выбор сделал другой генерал, пока не начнется бой. Платежная матрица в этом случае будет выглядеть следующим образом:

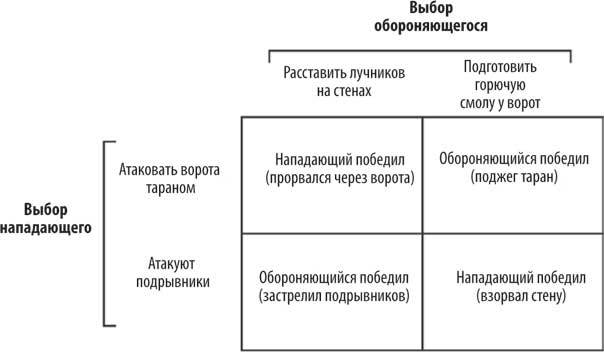
Как видите, наилучшего выбора в данном случае нет.

И вы, и обороняющийся принимаете решение, исход которого зависит от решения другого; каждый может победить, спрогнозировав ход противника. Вы не выиграете эту битву, имея больший таран, но у вас есть шанс, если вы попытаетесь понять, как обмануть соперника, заставите его думать, что вы будете атаковать ворота, но на самом деле начнете готовить саперов. Эта игра уже не о стенах и стрелах. Она о порядке действий, предположениях, информации и уловках. Теория игр помогает нам понять именно такую ситуацию.

Теория игр – это не только про соревнования. Она охватывает любые взаимодействия между игроками, которые должны реагировать на действия друг друга. Соревновательные игры с нулевой суммой, в которых может выиграть только один игрок, относятся к одной из этих категорий, сюда же относятся коллективные игры, а также смешанные соревновательные/коллективные ситуации, в которых цели игроков частично совпадают. Даже атака на защищенный замок не является стопроцентной игрой с нулевой суммой, потому что одна сторона может сдаться или предложить перемирие.

Один классический пример теории несоревновательных игр описывает двух доисторических охотников, Тага и Бларга. Так как они живут в разных племенах, они не могут заранее договориться о том, кто на кого пойдет охотиться. Каждый должен выбрать, отправиться ли на охоту на оленей или на зайцев. Если оба решают охотиться на оленей, они могут скооперироваться и завалить одного оленя, и тогда оба будут сыты. На зайцев можно охотиться в одиночку, так что любой, кто выберет зайца, получит небольшой, но гарантированный обед. Но если один выберет охоту на зайца, а другой пойдет на оленя, то охотник на оленя останется голодным.

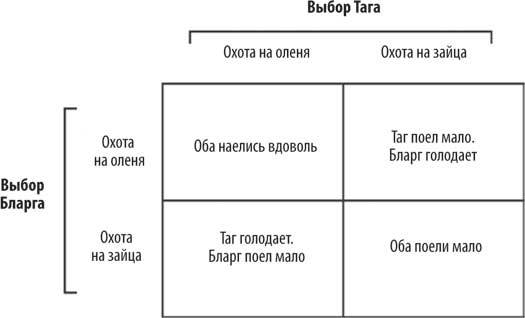
Как и в битве за замок, выбор Тага зависит от выбора Бларга, и наоборот.

Процесс принятия решения одним пещерным человеком не столько связан с оленями и зайцами, сколько с прогнозированием решения другого пещерного человека. Каждый должен думать не только о том, насколько голоден он сам, но и о том, насколько голоден его противник и насколько голодным он себя считает и так далее.

Вспомните ментальный слой переосмысления навыков – психологическую интеллектуальную игру, похожую на покер, в которой каждый игрок пытается предсказывать ход мыслей противника и манипулировать ими. Это теоретико-игровое мышление. Если кто-то еще активно думает о вашей игре, она становится чем-то большим, чем просто механика. Она становится линзой, через которую взаимодействуют два разума, и каждый пытается окутать другого в свою собственную ментальную модель. Для соперников игроков нет победы слаще.

Игры и стратегические взаимодействия

Прежде чем мы продолжим, я хотел бы уточнить одно определение. Специалисты по теории игр употребляют слово игра не так, как геймдизайнеры. Для них игра – это конкретное взаимодействие между стратегиями. Например, один раунд игры в «камень, ножницы, бумага» в теории игр считается игрой. В геймдизайне игра представляет собой целую систему механики, а не отдельную точку принятия решения.

Чтобы подчеркнуть разницу, я буду называть игры теории игр стратегическим взаимодействием. Игры, которые мы разрабатываем, генерируют множество стратегических взаимодействий, каждое из которых можно рассмотреть отдельно с помощью теории игр.

В этом простом вопросе определения может скрываться причина, по которой геймдизайнеры так часто игнорируют теорию игр. Теория игр не может просчитать целый раунд Mortal Kombat, поэтому многие сразу же считают, что анализировать игру бесполезно. Но это лучший способ проанализировать конкретное секундное взаимодействие между ударами, блоками или бросками. Теория игр не может охватить весь футбольный матч, но она может предсказать, куда игрок будет бить и в какую сторону прыгнет вратарь. Она работает только при применении на уровне взаимодействия между стратегиями, а не целыми дизайнами.

Равновесие Нэша

Основным понятием теории игр является равновесие Нэша.

Давайте разберемся.

Первая составляющая равновесия Нэша – это набор стратегий. Набор стратегий – это просто набор возможных выборов, которые могут сделать все игроки. Каждая ячейка в платежной матрице является набором стратегий. В примере с охотой на оленя, где Бларг охотится на оленя/Таг охотится на зайца, – это набор стратегий. То же самое в примере, когда оба охотятся на зайца, Бларг охотится на зайца/Таг охотится на оленя и оба охотятся на оленя.

РАВНОВЕСИЕ НЭША – это набор стратегий, при которых ни один игрок не может улучшить свой собственный результат, изменив только свою стратегию.

Равновесие Нэша – это просто особая комбинация стратегий. В частности, это тот случай, когда ни у одного из игроков нет причин менять стратегию, если они предполагают, что никто другой этого не сделает. Звучит нелогично, но это отличная идея.

В примере с охотой на оленя существуют два равновесия Нэша. Первое – когда оба выбирают охоту на оленя. В этом случае оба получают наилучший возможный результат; если кто-то изменит свою стратегию и захочет охотиться на зайца, количество пищи, которую он получит, уменьшится. Второе – когда оба выбирают охоту на зайца. Это более интересный случай, так как он раскрывает тонкость равновесия Нэша, которая заключается в том, что оно не обязательно оптимально для всех. Если оба охотятся на зайца, то они оба теоретически могут передумать и совместно отправиться на охоту за оленем, получив при этом гораздо больше еды. Но если передумает только один из них, он в конечном итоге останется голодным, в то время как другой будет жевать зайца. Итак, равновесие Нэша – это если оба пойдут охотиться на зайца, хотя это и не самый лучший вариант для любого из охотников.

Равновесия Нэша важны в реальных многопользовательских играх, потому что игра тяготеет к ним. Равновесия Нэша стабильны и самостоятельны, потому что ни у одного игрока нет причин делать что-то другое. Неравновесные конфигурации нестабильны и самомодифицируемы, поскольку у кого-то есть причина единолично изменить свою стратегию. Игра может допустить миллион комбинаций стратегий, но фактически будет присутствовать только равновесие Нэша. Таким образом, игровой опыт будет состоять из тех ситуаций, которые являются равновесиями Нэша – других вполне может и не существовать.

Вот почему так важно настроить игру так, чтобы у стратегических взаимодействий было большое количество или отсутствие чистых равновесий Нэша.

Стратегическое взаимодействие с одним равновесием Нэша в чистых стратегиях – испорченный геймдизайн, потому что он всегда будет находиться в том же равновесии. У каждого игрока только один жизнеспособный вариант, поэтому стратегическое решение исчезает.

При одном равновесии все игроки точно знают, что делать, и у них нет никаких оснований ждать или даже думать о шагах друг друга. Это монотонность. Исчезает интеллектуальная игра, в которой каждый игрок пытается просчитать решения других.

Ситуации с множеством равновесий, таких как охота на оленя, лучше, потому что теперь каждый игрок думает о том, что будет делать другой игрок. Но мы можем улучшить даже это.

Лучше всего, если равновесие Нэша убрать полностью. Например, в битве у замка нет чистого равновесия Нэша. Независимо от набора стратегий одна сторона может добиться большего успеха, изменив свой выбор. Это хороший геймдизайн, потому что всегда понятно, что будут делать другие игроки, а это создает чувство предвкушения, обмана и манипулирования другими людьми. Таким образом, если в вашем стратегическом взаимодействии существует равновесие Нэша, измените дизайн или баланс, чтобы избавиться от него.

Игры «камень, ножницы, бумага» и «орлянка»

Взаимодействия без равновесия Нэша обычно называют механикой «камень, ножницы, бумага», потому что камень – это самая известная игра без равновесия Нэша. В этой игре один игрок всегда хочет изменить свой ход независимо от набора стратегий. Платежная матрица игры выглядит так:

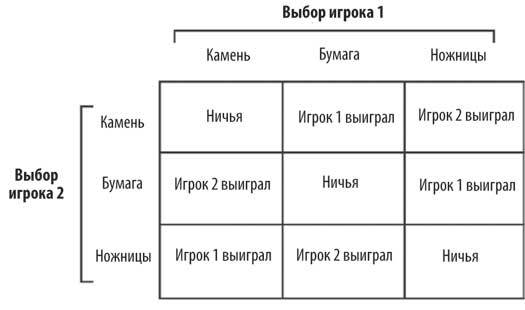
Но это легче представить так:

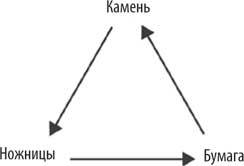
Подобная схема ходов и контрходов проявляется во многих формах в бесчисленных играх. В файтингах блок бьет панч, бросок бьет блок, а панч бьет бросок. В стратегиях копейщики бьют кавалерию, лучники бьют копейщиков, а кавалерия бьет лучников. Этот треугольник контрходов появляется снова и снова, так как это самый простой способ создать симметричную игру без равновесий Нэша.

Однако вопреки распространенному мнению, треугольник в игре «камень, ножницы, бумага» – не единственная базовая структура дизайна без равновесия Нэша. Вспомните битву за замок. Остается четыре хода, а не три. И у каждого игрока два варианта. Это не похоже на игру в «камень, ножницы, бумага», но, как вы видите, в этом случае равновесия Нэша тоже нет.

Паттерн игры «камень, ножницы, бумага» не образует равновесия Нэша для симметричных игр, в которых игроки ходят одинаково. Но в несимметричных играх, таких как битва за замок, мы используем другой паттерн, названный в честь другой старой игры – «орлянка».

В этой игре один игрок заявляет, что он ищет пару. Игроки не видят монетки друг друга. Каждый игрок кладет монетку орлом или решкой вверх. Затем они одновременно их раскрывают. Если монетки совпали, побеждает игрок, который искал пару. Если нет, побеждает его противник. Это выглядит следующим образом:

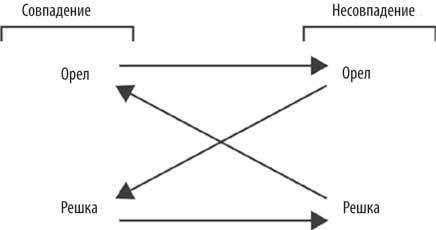
Хотя об этом часто и не говорят, но паттерн «орлянки» постоянно появляется в многопользовательских играх. Битва за замок – это аналогия «орлянки», потому что обороняющийся хочет, чтобы его оборона совпадала с вашим нападением, а вы хотите обратного. В многопользовательском шутере, когда вы защищаете объект в помещении с двумя дверями, вы играете в «сравнение монет»; вы хотите защитить дверь, через которую захочет атаковать соперник, а он, в свою очередь, хочет войти через другую дверь и выстрелить вам в спину. В стратегической игре World War II обороняющийся может решать, тратить ли ресурсы на установку мин, а нападающий может решать, тратить ли ресурсы на то, чтобы добывать тральщики. Вы не хотите расставлять мины, которые будут найдены, и вы также не хотите искать мины, которых нет.

Давайте рассмотрим реальный пример схемы «орлянки» в геймдизайне. В StarCraft II бои между игроками Зергами и Терранами часто ведут четыре юнита: Осадные танки Терранов и Морпехи, а также Гиблинги и Муталиски Зергов. Они взаимодействуют так:

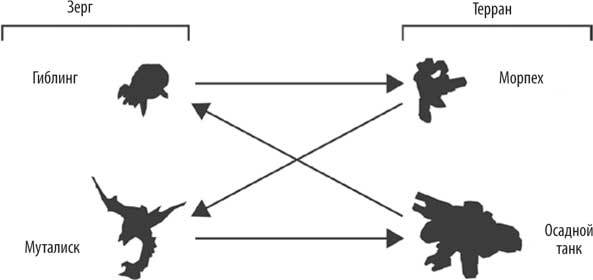
Муталиски летают, поэтому они автоматически поражают Осадные танки, потому что танки не могут стрелять в воздух. Сильнейший урон Морпехов мгновенно разрушает хрупких Муталисков. Гиблинг плавит плотно размещенные группы Морпехов, разбрызгивая кислоту. Но Осадные танки взрывают хрупких Гиблингов с безопасного расстояния. Многие раунды StarCraft II сводятся к повторяющимся взаимодействиям между этими четырьмя юнитами. По сети вы можете проиграть вариации этого паттерна сто часов подряд. Но игра никогда не становится скучной, потому что в ней нет равновесия Нэша, следовательно, у каждого игрока всегда есть возможность выиграть, просчитывая ходы своего противника или сбивая его с толку. Потому что на самом деле смысл игры не в управлении Морпехами и Муталискаими. Речь идет о том, чтобы угадать мысли противника.

«Камень, ножницы, бумага» и «орлянка» – единственные элегантные паттерны дизайна для стратегических взаимодействий – «камень, ножницы, бумага» для симметричных игр, а «сравнение монет» – для асимметричных. Любая альтернатива это не более чем бессмысленное нагромождение новых стратегий.

Например, в игре «камень-бумага-ножницы-ящерица-Спок» каждый символ бьет два других:

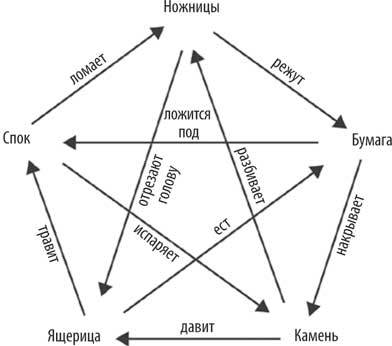
Но RPSLS («камень-бумага-ножницы-ящерица-Спок») ничего не выигрывает с точки зрения интереса к решению в RPS («камень, ножницы, бумага»). Если равновесия Нэша нет, то его нет. Дополнительные символы никак не улучшают интеллектуальную игру предвкушения и хитрости. Дополнительные варианты могут сделать сюжет более интересным, но, скорее всего, это не стоит дополнительного бремени обучения.

Смешанные стратегии

До сих пор я говорил о том, что в таких играх, как «камень, ножницы, бумага», нет равновесия Нэша. Это было не совсем точно. В этой игре нет чистого равновесия Нэша. Но зато существует смешанное.

СМЕШАННОЕ РАВНОВЕСИЕ НЭША – это равновесие Нэша, где каждый игрок произвольным образом выбирает из набора стратегий с некоторым заданным набором вероятностей.

Например, в игре «камень, ножницы, бумага» нет чистого равновесия Нэша, но есть одно смешанное. Игра предполагает, что оба игрока будут показывать каждый ход в 33,3 % случаев. Это равновесие Нэша, поскольку один игрок не может выиграть, отступив от этой схемы (поскольку если соперник показывает по чистой случайности, ваш ход не имеет значения, вы всегда выигрываете половину).

Другие стратегии в игре «камень, ножницы, бумага» не находятся в равновесии. Например, представьте, что вы должны были выбрать камень в 35 % случаев, а ножницы и бумагу – в 32,5 %. Теперь соперник может победить вас, изменив свою стратегию, выбирая бумагу в 100 % случаев. Если один игрок может выиграть, изменив свою собственную стратегию, это не равновесие Нэша.

Смешанные равновесия легко решить в таких простых играх, как «камень, ножницы, бумага» и «сравнение монет», в которых один игрок сразу выигрывает, а другой проигрывает. Но это необычный случай. В большинстве реальных стратегических взаимодействий разные исходы дают разные результаты. Например, в файтинге блок бьет джеб, не нанося урона, джеб бьет бросок, нанося немного урона, а бросок бьет блок, нанося много урона. Это аналог версии игры в «камень, ножницы, бумагу», где вы получаете 1 доллар, если выигрываете, показав бумагу или ножницы, и 5 долларов, если выигрываете, показав камень. Платежная матрица выглядит так:

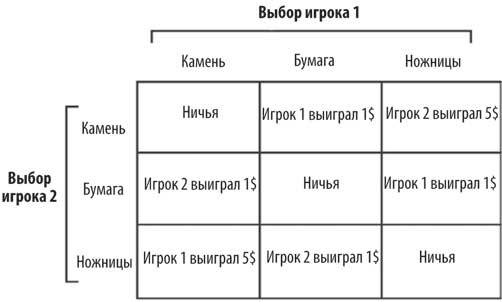
Показывать каждый раз камень и надеяться на 5 долларов – наивная стратегия.

Проблема в том, что это предсказуемо. Противник может показывать только бумагу, и вы уйдете ни с чем. Чтобы хорошо играть в эту игру, нужна смешанная стратегия, когда вы произвольно выбираете между камнем, бумагой и ножницами. Но вы не можете разыгрывать ходы равномерно, как в классической RPS, иначе соперник начнет просто показывать камень чаще. Так как часто нужно делать каждый ход, чтобы заработать максимум?

Здесь вступает в игру математический аспект теории игр. Учитывая стратегическое взаимодействие и выигрыши, специалисты по теории игр могут рассчитать точное соотношение в смешанной стратегии, которое образует равновесие Нэша. Геймдизайнерам не нужно делать количественный анализ, но важно понять соотношение, поэтому я продемонстрирую это на реальном примере.

В футболе при пенальти мяч летит со скоростью до 55 м/с. На этой скорости мячу требуется примерно одна пятая секунды, чтобы преодолеть расстояние от ноги подающего к цели. Вратарю недостаточно этого времени, чтобы прыгнуть и попытаться не пропустить мяч после того, как по нему уже ударили. Единственный выбор – прыгнуть до удара по мячу. В то же время подающий должен выбрать цель, не зная при этом, куда прыгнет вратарь.

Это игра под названием «сравнение монет». Вратарь хочет не пропустить гол, а подающий, наоборот, забить.

В этой игре платеж подающего – вероятность того, что он забьет гол. Его шансы на выигрыш при правильной блокировке выше при ударе вправо, чем влево, шансы забить без блокировки также выше вправо, чем влево. Конечно, его выигрыш остается лучше при ударе влево и отсутствии блокировки, чем при ударе вправо и наличии блокировки. В остальном удар вправо будет представлять собой чистую стратегию равновесия, которая будет непреднамеренно использоваться постоянно.

Лучшая стратегия для подающего – произвольно чередовать удары вправо и влево в разных пропорциях, в большинстве случаев забивая вправо, иногда разбавляя их офсайдами, чтобы вратарь не расслаблялся. В то же время вратарь должен отражать его, большую часть времени блокируя удары вправо, а иногда и удары влево.

Мы можем вычислить точные пропорции на основании вероятности, с которой футболист забьет для каждой из четырех возможных комбинаций со стороны подающего/стороны вратаря. Однако во время исследований были получены данные о сотнях ударов в играх Европейской лиги, на основании которых составлена следующая таблица процентного соотношения шанса забить гол (которая фактически является платежной матрицей):

Из этих цифр видно, что лучшая стратегия для подающего – забивать в правый угол 59,7 %, а в левый – 40,3 %. Эта смешанная стратегия дает общий шанс успеха на уровне 74,0 % независимо от действий вратаря.

Любое отступление от этого соотношения позволяет вратарю улучшать свои результаты, выбрав чистую стратегию прыжков только вправо или влево. Например, если бы подающий забивал вправо 65 % ударов, а не 59,7 %, у него бы только 72,6 % ударов по воротам, при этом вратарь использовал бы свою стратегию прыжков только вправо.

Ключ к смешанному равновесию Нэша в том, что в равновесии каждый возможный ход имеет равный платеж.

Используя равновесную стратегию при любом ударе, нападающий рассчитывает на 74,0 % вероятности попасть в цель независимо от того, в какую сторону была подача. Используя равновесную стратегию, на любом ударе подающий рассчитывает на то, что вероятность забить гол составляет 74,0 % независимо от того, с какой стороны он бьет. Если бы он рассчитывал на большую вероятность для любой из сторон, вратарь чаще отвечал бы, прыгал на эту сторону, снижая коэффициент успешности для этой стороны. Это свойство равных платежей является полезным способом для понимания равновесных стратегий без математики. Просто посмотрите на пропорции, где каждый вариант приводит к одному и тому же среднему платежу.

Могут ли игроки реально проводить такой численный анализ? Нет, но в среднем среди многих игроков можно найти людей, которые замечательно справляются с поиском оптимальных смешанных стратегий на интуитивном уровне. Исследования реальных показателей футбольных подач показывают, что подающие в целом бьют справа почти полностью с правильной частотой.

Итак, неужели это все? Мы просто просчитываем платежи, определяем соотношение смешанной стратегии, и пусть игроки подбрасывают свои монеты? К счастью, нет. В реальных играх взаимодействие в теории игр является лишь основой для взаимодействия, ориентированного на человека, называемого yomi.

Yomi

Я позаимствовал термин yomi у Дэвида Сирлина, геймдизайнера файтингов, который, в свою очередь, взял его из японского слова «чтение» (чтение мыслей противника). Переворачивать монеты неинтересно, а вот пытаться читать мысли человека – очень интересно. Вот почему такие паттерны дизайна, как «камень, ножницы, бумага» и «сравнение монет», являются лишь скелетом игры. Эмоциональную ценность игре придает именно плоть – yomi, умение заставить противника думать, что вы сделаете одно, а на самом деле вы сделаете другое, или позволить противнику думать, что он обманул вас, хотя на самом деле вы все поняли, или возможность пустить в ход такое оружие, о котором ваш противник и не догадывался. Это интенсивные и глубокие формы ментального конфликта.

YOMI – это интеллектуальная игра прогнозирования, хитрости и стремления переиграть соперника, чтобы получить выигрыш, выходящий за рамки математики теории игр.

Yomi работает, потому что реальный мир более неоднозначный, чем математика. В сухом математическом анализе исчисляется каждый платеж, а каждая стратегия четко отличается от других. Но настоящие игры не такие. Их исход невозможно определить количественно, стратегии нельзя аккуратно разместить в ячейки, а у игроков нет полной информации или доступа к генераторам случайных чисел.

Например, в шутере оба игрока должны решить, перезаряжать ли оружие за углом, бросить гранату или подождать, держа дверь под прицелом, но они также могут в любой момент изменить свое решение или даже выполнить два действия одновременно. В игре жанра «стратегия» игроки выбирают экономические стратегии, которые плавно смешивают различные производственные задачи. В каждом случае существуют неоднозначные, не поддающиеся количественному определению границы вокруг взаимодействия в теории игр. Играющий в жанре «шутер» может смотреть и двигаться плавно во всех направлениях, играющий в стратегию может заказать продукцию тысячами разных способов. Эти размытые границы – то, откуда появляется yomi. Это то, что позволяет игрокам обойти границы математики, незначительно менять платежную матрицу каждого решения и узнавать чуть больше или чуть меньше о сопернике, чтобы опередить его в игре.

Таким образом, игра yomi зависит не только от создания стратегического взаимодействия без чистого равновесия Нэша, но и от создания системы с интересными размытыми границами вокруг этих взаимодействий. Давайте рассмотрим некоторые способы, с помощью которых мы можем генерировать подобное стратегическое взаимодействие.

Yomi растет, если игроки могут плавно переходить от одной стратегии к другой.

Yomi требует, чтобы в игре были детализированные стратегии, которые можно смешивать и комбинировать сложными способами. Например, в StarCraft II игрок за Терранов может составить войско из половины Осадных танков и половины Морпехов. Его не остановят ни войско из одних Муталисков, ни войско из Гиблингов. Для контратаки нужна аналогично смешанная армия Муталисков и Гиблингов. Терран может понемногу менять свое войско – плюс-минус один Морпех, плюс-минус один Осадный танк. Эти два игрока не играют в лабораторную игру, в которой нужно проверить одну коробку и сравнить ее с другой, чтобы узнать результат. Они не просто забивают мяч влево или вправо. Они играют в ровном стратегическом пространстве, которое позволяет им выбирать из почти бесконечного множества промежуточных комбинированных стратегий. Каждая хорошо определенная стратегия требует аналогичной хорошо определенной реакции.

Хорошо определенные стратегии дают yomi, потому что они позволяют игрокам превосходить друг друга в нюансах своих стратегических знаний. Кому угодно можно сказать, что Морпехам противостоят Гиблинги, а Осадным танкам – Муталиски. Но только эксперты точно знают, что нужно, чтобы победить группу Морпехов и Осадных танков. Что будет, если у него пятнадцать Морпехов и один Осадный танк? Что будет, если у него восемь Морпехов и пять Осадных танков? Какое минимальное количество понадобится для уничтожения? Новичок этого знать не будет, а эксперт будет. Этот вид мелкослойного взаимодействия – то, что толкает потолок мастерства игры вверх.

Игра Yomi растет из сложных, с трудом поддающихся количественной оценке платежей.

У разных стратегий разные потенциальные платежи. На примере игры «камень, ножницы, бумага» мы рассмотрели вариант, в котором вы получаете 5 долларов, если бросили камень и победили, и 1 доллар – если бросили бумагу или ножницы и победили. Изменение этих показателей меняет пропорции стратегий, по которым должны играть игроки. И, как вы помните, правильные пропорции – это те, в которых у каждой отдельной стратегии одинаковый средний платеж.

Но что, если бы у нас не было этих значений? Что, если бы в стратегиях были потенциальные платежи с качественными эффектами, объединяющимися в несколько целей на разных уровнях достоверности? Эти платежи не известны заранее, и их нельзя описать одним значением. Определение хорошей смешанной стратегии перестает быть просто вопросом уравнивания платежей различных стратегий. Сначала мы должны выяснить, что такое платежи. Этот процесс вычисления поддерживает поток и повышает потолок мастерства.

Неопределенные платежи также означают, что нам нужно угадать, как другой игрок оценивает свои платежи. Если вы хорошо знаете своего противника, вы можете найти место, где он переоценивает или недооценивает определенные платежи, и использовать его, чтобы спрогнозировать его поведение и победить. На еще более высоких уровнях мастерства вы можете спрогнозировать его предположения о ваших оценках и так далее.

Вернемся к StarCraft II. Муталиски и Осадные танки стоят дорого, а Морпехи и Гиблинги – дешево. Это значит, что играющий за Терранов получит более высокий платеж за убийство Муталисков и Морпехов, чем за Гиблингов и Осадные танки, поскольку Муталисков сложнее заменить, а Морпехов легче построить. Это же правило работает и в обратном направлении: Зерги хотят уничтожить Осадных танков и Муталисков больше, чем Морпехов и Гиблингов.

Если бы все было так просто, это взаимодействие все еще можно было бы решить математически путем включения точного значения каждого вида персонажей. Но реальные последствия зависят не только от стоимости персонажей. Они зависят от того, как эта битва развивается через другие игровые системы, и ее контекста в более крупной игре.

Рассмотрим контекст. Если Осадные танки Терранов медленно приближаются к базе Зергов и почти достигли расстояния, с которого можно начать бомбардировку, Зергам крайне необходимо уничтожить атакующую силу любыми средствами. Если они этого не сделают, то им придется заплатить гораздо дороже, если бой случится где-то посередине карты. Если вы упустите что-либо на карте, ваши боевые единицы погибнут. Если вы упустите что-либо на месте, ваша база будет разрушена. Поэтому последствия могут быть разные.

Расстановка может изменить последствия. Рассредоточенные Морпехи и Осадные танки уязвимы для набрасывающихся на них Муталисков. Но сосредоточенные войска уязвимы к брызгам кислоты Гиблингов. Группа Морпехов, которая обычно уязвима для Гиблингов, может не пострадать, если она разбросана по обширной территории. В то же время эта разобщенная группа становится чрезмерно уязвимой для Муталисков, улучшая последствия.

Последствия также меняются в зависимости от количества единиц армии. Например, мы знаем, что Гиблинг обычно побеждает Морпеха. Но если Морпехов достаточно, они могут победить небольшое количество Гиблингов без потерь, стреляя в них до того, как те приблизятся. Точно так же, хотя Морпехи обычно отражают атаку Муталисков, большая группа Муталисков может уничтожить небольшую группу Морпехов без потерь. В этих случаях в результате отсутствия баланса в цифрах взаимоотношения в базовой игре в сравнении монет изменились. Но это изменение не происходит повсеместно – ни одно количество Гиблингов не сможет уничтожить один Осадный танк.

Изменение навыков влияет на последствия. Один игрок может мастерски играть Муталисками, улучшая последствия за счет этой стратегии. Следовательно, он захочет больше играть Муталисками, чем Гиблингами. Другой игрок захочет нанести ответный удар Морпехами, а не Осадными танками, так же как вратарь чаще прыгает на сторону, куда подающий забивает чаще.

Еще более простые игры представляют платежи, меняющиеся в зависимости от ситуации, хотя и в меньшем объеме. Например, в файтингах не так много переменных, как в StarCraft II. Присутствуют два персонажа, каждый из которых находится в определенном состоянии, и у ситуации не так много исходов. Тем не менее существует достаточно комбинаций позиций, состояния анимации, здоровья, энергии и других переменных, поэтому оценка платежа является сложной задачей для ума. Решение имеет меньшую значимость, чем в StarCraft II, но это допустимо, потому что оно сжимается до доли секунды. Сложность решения пропорциональна времени, доступному для его принятия, поэтому поток не прерывается.

При каждом взаимодействии игроки должны оценивать переменные и расчетные вероятности, чтобы составить набор оцененных платежей. В StarCraft II они должны учитывать количество боевых единиц, расположение, различия в навыках, статус экономики, экономическое влияние и сотни других количественных и не поддающихся количественному определению переменных. Задача высокой степени сложности, но в этом и состоит сила человеческой мысли. Машины не могут делать подобные расчеты. Только работающий на полную мощность человеческий мозг, используя все свои геометрические, пространственные, эмоциональные и межличностные познания, может решить эту проблему. Это тренировка всех частей, тренировка целого мозга.

И этот процесс оценки – не просто логическая головоломка. Это также эмоциональный вызов. Заурядные игроки, играющие за Зергов, будут паниковать и атаковать преждевременно, как только Осадные танки начнут обстреливать несущественную базу.

Начинающие Терраны по глупости оставят свои танки без присмотра, пока их Морпехи будут жадно преследовать Муталисков. В каждом случае эмоции этих игроков омрачают их оценку платежей. Зергом движет эмоциональный страх потери; матерые игроки знают, что иногда лучше потерять базу, чем рисковать армией, чтобы спасти базу. Терраном движет алчная жажда убить дорогого Муталиска; более подкованные игроки знают, когда их отпустить. Научиться хорошо оценивать – не значит просто знать и продумывать логику. Это значит оценивать свои эмоции, тренировать их и держать под контролем.

Эти сложные логические и эмоциональные задачи заставляют игроков снова и снова возвращаться и поднимают уровень мастерства до непостижимых высот. Эта глубина означает, что независимо от того, насколько вы хорошо умеете оценивать, всегда существует другой нюанс, который нужно обнаружить и учесть.

А вы знали, что существуют настоящие турниры по игре в «камень, ножницы, бумага»? Люди регистрируются, проходят отборочные туры и соревнуются на глазах у зрителей. Призы могут достигать 50 тысяч долларов. И все это в игре, где единственная равновесная стратегия – быть абсолютно случайным.

Yomi вырастает из психологии случайности.

Звучит как шутка, и в некотором смысле так оно и есть. Но, тем не менее существует навык игры в «камень, ножницы, бумагу» против человека, потому что люди не могут генерировать случайные числа.

В теории игр смешанные стратегии должны быть идеально случайными. Но так как люди не могут генерировать случайные числа, мы никогда не сможем играть в настоящие смешанные стратегии. Наш разум наполнен хорошо изученными вероятностными искажениями. На просьбу написать случайную строку из 1 и 0 мы постоянно чередуем числа чаще, чем следует. Длинные повторения одного символа кажутся нам менее вероятными, чем они есть на самом деле. Если мы только что проиграли в стратегии, наше мнение о ее ценности в следующей игре изменилось. Мы можем использовать подобные ошибки в свою пользу. Например, вы можете играть в игру прогнозирования ошибок в мысленном генераторе случайных чисел других игроков. Если вы понимаете кого-то и подкованы в yomi, вы можете сказать, когда человек покажет камень, с вероятностью 35 %, даже если он пытается показать с вероятностью 33,33 %. И вы можете превратить эти знания в победу. Опять же, это толкает потолок мастерства вверх и улучшает решения.

Yomi растет от манипулирования информацией.

Принятие стратегических решений зависит от наличия полезной и полной информации об игре. Игроки должны знать, что происходит, что знает их соперник и что он думает и так далее. Обе стороны могут манипулировать всей этой информацией, если позволяет геймдизайн, создавая возможности для yomi.

Существуют три основных способа, которыми игроки могут манипулировать информацией.

Во-первых, игроки могут искать информацию, чтобы улучшить свои собственные решения. В стратегиях игроки отправляют разведчиков. В играх социального взаимодействия игроки спрашивают своих друзей. В шутерах они останавливаются и слушают шаги. Такие инструменты, как датчик сердцебиения в Modern Warfare или возможность сканирования в StarCraft II, обеспечивают выполнение подобных действий.

Во-вторых, игроки могут отказаться предоставлять кому-либо информацию. В стратегиях они убивают разведчиков. В играх социального взаимодействия они вмешиваются в разговоры других людей. В шутерах они бросают дымовые шашки или антирадары. Игроки могут даже скрыть метаигровую информацию – известно, что участники турниров как по StarCraft, так и Street Fighter экономят свои лучшие ходы в ранних раундах только для того, чтобы реализовать их в финале.

Наконец, игроки могут предоставлять ложную информацию, чтобы обмануть друг друга. В то время как другие виды yomi предполагают знание мыслей противника, обман – это контроль над ними. Иногда механика обмана может быть явной, как в стратегических фантомных войсках или в играх социального взаимодействия. В других случаях игроки найдут способы использовать для этого обычную механику. Например, в шутере игрок может открыть дверь, чтобы создать ложное убеждение в том, что он проходит через нее, но по факту войти через окно. В стратегической игре игрок может построить аэропорт, позволить противнику разведать его, но так и не создать самолет, при том что противник инвестирует в бесполезное противовоздушное оружие.

Эти элементы дизайна манипулирования информацией можно расширить для создания слоев ложной информации. Один игрок может заставить другого игрока думать, что он знает то, чего на самом деле не знает. Или он может заставить другого игрока думать, что он не знает факта, который на самом деле знает. Этот вид многослойного обмана сложно разработать напрямую, но это ценный результат, который может появиться в случае взаимодействия основных инструментов обмана.

Для Yomi не нужно большое количество игроков.

Трудно в уме смоделировать мысли другого игрока. Наблюдение за намерениями и привычками двух или трех человек находится на грани возможного. Увеличьте количество игроков до четырех и более, и это уже будет невозможно. Поэтому yomi ограничивается двумя-тремя игроками, так как получается слишком много чужих мозгов, о которых нужно думать. При большом количестве игроков игра теряет свой интеллектуальный аспект и становится только механикой.

Очевидный способ решить эту проблему – сохранить небольшое количество игроков. Но часто это не выход. В этих случаях игра все еще может создать yomi, на время изолируя небольшие группы игроков от основной массы.

Например, в World of Warcraft играют миллионы игроков, но они всегда взаимодействуют в небольших, ограниченных группах. Четыре игрока могут отправиться в рейд в подземелье, чтобы получить добычу, два игрока могут провести поединок. Специальная игровая механика не позволяет разным группам сталкиваться друг с другом. Таким образом, yomi может расти внутри группы, пока она изолирована.

Изоляция также может происходить с помощью более мягких и эмергентных механизмов. Например, во многих шутерах игроки объединяются в большие команды по 16 и более игроков. Но не каждый игрок постоянно сражается. Скорее они рассредоточены по большой карте со множеством изолированных комнат. Бои начинаются и заканчиваются в одном помещении, и в них не участвует большое количество игроков. Это позволяет игрокам сосредоточиться только на тех, кто присутствует в комнате, что делает yomi возможным, даже если на поле будут 32 игрока.

Yomi. Кейс: modern Warfare 2

Давайте рассмотрим пример игроков, использующих yomi, в многопользовательском шутере Modern Warfare 2. Этот пример охватывает несколько секунд игры между Кэрол и Дейвом в режиме Team Deathmatch.

Кэрол внутри маленького сарая с двумя входами, она видит приближающегося Дейва. Она отступает дальше вглубь, чтобы оба игрока не видели друг друга.

Начинается теоретико-игровой мыслительный процесс, запускающий yomi. Эти игроки начали играть в игру «сравнение монет», поскольку каждый выбирает между двумя входами в сарай. Кэрол может видеть один вход, а Дейв хочет атаковать через вход, на который Кэрол не смотрит, и подходит к ней сзади.

Если бы это было все, игроки могли бы рассчитать соотношения смешанной стратегии, перевернуть монеты и продолжить. К счастью, чтобы игра была интересной, в Modern Warfare 2 множество нечетких границ, образующих yomi вокруг своей основной игровой механики.

Вот как выглядят мысли Кэрол, пока она обдумывает свои варианты.

Она может либо остаться в сарае, либо выбраться из него через любую дверь. Если Кэрол решит остаться:

• Она может сосредоточиться на одной двери. Если Дейв войдет в эту дверь, он попадет прямо под ее прицел и она выстрелит, мгновенно убив его. Если Дейв войдет через другую дверь, он выстрелит ей в спину, прежде чем она успеет обернуться. Но за какой дверью ей следить?

• Она может решить следить за дверью, через которую увидела Дейва. Дэйв может это спрогнозировать и пойти со спины. Она может это спрогнозировать и так далее.

• Она может решить следить за дверью, которая ближе к Дейву, затем, не видя его, переключиться на другую дверь. В этом случае она опирается на тот факт, что Дейв еще не атаковал, эта информация указывает на то, что он мог выбрать другой путь. Опять же, Дейв мог предугадать данную цепочку рассуждений и действовать вопреки ей.

• Она может смотреть то на одну дверь, то на другую. Это защита. Такое наблюдение означает, что она увидит Дейва почти сразу после того, как он войдет. Недостатком является то, что Кэрол сама себя дезориентирует и нарушает прицел, постоянно переводя взгляд с одной двери на другую. Даже если Кэрол будет видеть дверь, когда в нее войдет Дейв, ее прицел, скорее всего, будет не совсем точным, в отличие от ситуации, если бы она постоянно целилась в одну дверь.

• Она может решить постоянно перемещаться в сарае. Опять же, это защита. Перемещение делает Кэрол более трудной целью, поэтому Дэйву, скорее всего, будет сложнее убить ее, даже если он войдет в дверь, пока Кэрол не видит. Недостатком этого решения является то, что это нарушает прицел Кэрол, а также может создавать звуки шагов, по которым Дэйв сможет узнать о присутствии Кэрол, ее местонахождении и активности.

• В любое время Кэрол может перестать ждать и целиться снаружи.

Если Кэрол решит целиться из сарая, она может или столкнуться с Дейвом, или не столкнуться:

• Если она встречает Дейва, yomi-игра заканчивается, так как оба игрока находятся в поле зрения друг друга и никакой существенной скрытой информации больше нет. Игра превращается в задачу «застрелить-увернуться». Первоначальное преимущество в этой стрельбе зависит от того, насколько хорошо Дейв спрогнозировал ход Кэрол.

• Если по прогнозу Дейва Кэрол выйдет из сарая через правильную дверь, он, возможно, просто встанет перед дверью и наведет на нее пистолет. В этом случае Кэрол идет прямо на него и почти наверняка умирает.

• Если по прогнозу Дейва Кэрол выйдет из сарая, но он не знает, через какую именно дверь, Дейв может просто находиться поблизости, пытаясь наблюдать за обеими дверьми, не концентрируя внимание только на одной. Эта стратегия защиты приводит к относительно справедливому соревнованию по стрельбе, так как ни один из игроков не целится в другого.

• Если, выйдя из сарая, Кэрол не сталкивается с Дейвом, у нее несколько вариантов в зависимости от того, что, по ее мнению, делает Дейв.

• Она может обойти сарай и попытаться подойти к Дейву сзади, когда он подходит к другой двери. Если Дейв замешкается, Кэрол, возможно, сможет подойти сзади и выстрелить ему в спину. С другой стороны, если Дейв дошел до двери быстро, он, возможно, уже заглянул внутрь и обнаружил, что Кэрол вышла через первую дверь. Теперь он может либо развернуться и ждать, пока Кэрол обойдет сарай, вероятно, после этого убив ее, либо решить, что Кэрол сбежала через другую дверь, и в этом случае он пробежит через сарай и выйдет с другой стороны.

Кэрол может попытаться убежать:

• Если бы Дейв быстро обошел вокруг сарая, возвращаясь, он бы выстрелил в спину Кэрол, когда она убегала.

• Если по прогнозам Дейва Кэрол сбежит, он, возможно, вообще не подходил к сараю и просто прятался на расстоянии, и в этом случае он застрелит Кэрол.

• Если Дейв замешкался на подходе к другой двери, Кэрол сможет сбежать.

На первый взгляд Modern Warfare 2 выглядит как игра о стрельбе в людей. Вот почему ее называют шутером. А стрельба здесь наиболее безобидное слово. Целься, атакуй, взрывай и бросай. Хорошее бессмысленное веселье, правда?

Но если бы это было все, игроки быстро бы устали. Стрельба – это просто зрелище. Оно не долговечно, но в Modern Warfare 2 оно есть. Люди играют в эту игру сотни или даже тысячи часов. Они покупают сиквел за сиквелом, чтобы делать одно и то же снова и снова. Почему?

Потому что на самом деле эта игра не о стрельбе. Все дело в yomi, это сложный танец интеллектуальной оценки и переоценки. Опытные игроки действительно продумывают разветвленные возможности в реальном времени. Это то, что переживает их разум, он не зациклен на повторяющейся графике стрельбы. Это далеко не бессмысленная игра рассчитана на интеллектуалов.

Основная причина, по которой Modern Warfare 2 так хорошо создает yomi, заключается в том, что ее оружие чрезвычайно точное и смертельное. Игроки умирают за один-два выстрела. Если вы подошли к кому-то сзади, он умирает до того, как у него появится шанс повернуться и выстрелить. Это означает, что значимые решения – это не те решения, когда игроки стреляют друг в друга, а те, которые принимаются до того, как игроки увидят друг друга. Вы хотите быть тем игроком, который подходит к противнику сзади, а не наоборот. И yomi процветает, когда игроки не видят друг друга, изо всех сил стараясь услышать шаги, наблюдая за датчиками сердцебиения, прислушиваясь к выстрелам и угадывая пути атаки врагов. Если нет полной информации, появляется масса возможностей для обмана.

Этого не происходит в шутерах с более слабым оружием. Первый выстрел не стоит того, чтобы потратить 25 выстрелов и кого-то убить. В таких играх неважно, что делают игроки, когда не видят друг друга. Важно то, насколько хорошо они целятся и уклоняются во время боя. И хотя прицеливание и уклонение от атак являются сложными задачами механики, в них нет yomi, так как отсутствует значимая скрытая информация.

Modern Warfare 2 на самом деле создает гораздо больше нюансов и разнообразных yomi, чем дерево решений в предыдущем примере. В реальной игре у каждого игрока больше опций и информации, они являются более нечеткими и более тонкими, чем здесь описано. У игроков могут быть специальные инструменты, которые могут помочь им собирать или скрывать информацию, например оглушающая граната, дымовые шашки, способность передвигаться бесшумно, датчики сердцебиения и так далее. Любой игрок может рассеивать пули, выдавая свою позицию, но надеясь на попадание. Любой игрок может выстрелить через пролет, чтобы попытаться дать ложные сигналы. Игроки могут общаться с членами своей команды или просто ждать и надеяться на помощь от союзника, который оказался неподалеку. У игроков могут быть различные типы оружия, поэтому любой из них может иметь преимущества или недостатки в любом типе столкновения – Кэрол может предпочесть ближний бой и автомат, а Дейв – сражаться на расстоянии и винтовку. В ориентированной на цель игре один или оба игрока могут хотеть не только победы. Если тикает таймер, проигрывающий игрок не будет использовать стратегии, которые отнимают ценные секунды; другой игрок может спрогнозировать это и тянуть время. У игроков может быть разный общий уровень мастерства и способности в определенных навыках, например в прицеливании, движении или непосредственно в yomi, и каждый может знать о другом игроке либо много, либо ничего. Игроки могут быть измотанными, возбужденными, рассеянными или расстроенными. Соберите все это в кучу, и вы поймете всю сложность решений, насквозь пронизанных yomi.

И это только один выбор, продолжающийся одну или две секунды. Игра будет продолжать генерировать эти тактические головоломки тысячами, каждая из которых перетекает в следующую, никогда не повторяется и не дает игроку почувствовать скуку. Она поддерживает поток путем непрерывного обмана, который преподносится через простую, тщательно продуманную механику.

Разрушительное поведение игрока

Большинство игр задают игрокам цели: набрать наибольшее количество очков, победить соперника или выжить как можно дольше. До сих пор мы предполагали, что на самом деле игроки достигают этих целей только потому, что мы им так сказали. Но иногда они этого не делают.

В однопользовательской игре, когда игроки преследуют цели, которые не ставил перед ними дизайнер, деск-джампинг дает свои результаты. Однопользовательский деск-джампинг может навредить опыту, но обычно это не смертельно. Однако в многопользовательской игре придуманные игроком цели могут разорвать игру на части, потому что эти цели затрагивают каждого, а не только того, кто их придумал.

Многопользовательские игры обычно хорошо структурированы и хорошо сбалансированы, поэтому у каждого игрока определенная роль. Один игрок, делающий странный выбор, нарушает этот баланс и разрушает игру для всех, включая тех, кто хотел играть нормально. Например, если группа героев сражается с драконом и один из сражающихся решает отлучиться на трапезу или вылечить дракона просто из любопытства, тогда вся команда проигрывает.

Существуют два основных вида деструктивного поведения игрока: разные цели и разные навыки.

Разные цели

Я уже писал о достоинствах Modern Warfare. Теперь пришло время взглянуть на один из ее недостатков: разные цели. Официальная цель каждой многопользовательской миссии – победить. Каждый тип игры устанавливает различные критерии победы. Например, в игре Capture the Flag цель заключается в том, чтобы за ограниченное количество времени захватить больше флагов, чем команда соперника. Проблема в том, что игра еще и отслеживает количество убитых каждым игроком врагов и сохраняет эту информацию в базе данных для постоянного хранения данных. Уничтожение врагов всегда приятнее, чем наблюдение за счетчиком в углу экрана. В результате некоторые игроки предпочитают игнорировать официальные цели, в данном случае захват флага, и сосредоточены исключительно на уничтожении врагов. Это не вредит их опыту, но мешает опыту других игроков. Их союзники вынуждены играть с теми, кто не будет захватывать цель, а их соперники столкнутся с нечестной игрой.

РАЗНЫЕ ЦЕЛИ появляются, если игроки в многопользовательской игре решают добиваться целей, которые нарушают опыт других игроков.

Единственная причина, по которой дизайн Modern Warfare все еще держится на плаву, заключается в том, что уничтожение врагов обычно помогает в достижении командных целей. Игрок, который не думает о захвате флага, продолжает помогать, если он убивает врагов. Существует другая цель, но она все еще достаточно тесно связана с официальной целью, поэтому игра в основном работает. Конечно, это вредит игре, но не уничтожает ее полностью. Если бы другая цель заставила игроков действовать полностью против официальных целей, то игра бы развалилась. Например, Left 4 Dead – это игра о четырех выживших, помогающих друг другу пережить наступление зомби. Игра разработана таким образом, что команда достигает наибольшего успеха, если действует сообща. Но иногда один игрок может отступить и захотеть проверить, как далеко он может пройти один, просто чтобы бросить вызов самому себе. Но это разрушает игровой опыт членов его команды. Он получает непроходимый, но интересный бой, который и хотел, а его команды лишаются его помощи и тщательно сбалансированная игра расстраивается.

Даже реальные действия, такие как выход из многопользовательской игры, являются формой разных целей. У игрока, выходящего из игры, цель встать и заняться чем-то другим. Цель оставшихся игроков – продолжить играть.

Но худшие виды отличных целей – это те, которые основаны на удовольствии вызывать у других раздражение. Это называется вредительством.

ВРЕДИТЕЛЬСТВО – это сознательное разрушение чужого игрового опыта ради собственного развлечения.

В шутере игроки перекрывают вход, чтобы их команда не могла покинуть стартовую зону. В стратегиях игроки атакуют своих союзников или блокируют свои базы. Даже в играх, в которых нет очевидного способа причинить вред другим игрокам, поиск способов вредительства становится непосредственно самой игрой. Игроки World of Warcraft накладывали заклинание «хождение по воде» на союзников, когда те падали с высоты в бассейн. Несчастные жертвы падали в воду, которая для них внезапно оказывалась твердой, как бетон. Игроки Counter-Strike использовали функцию граффити, чтобы размещать ужасно оскорбительные изображения в высокопроходимых зонах уровня. Другие игроки, пытаясь сражаться в тактических битвах, были вынуждены смотреть самые шокирующие картинки интернета (а ведь такой тип сопоставления не улучшает опыт).

В очных играх, например в настольных, спортивных состязаниях или бильярде, люди не занимаются вредительством из-за угрозы разрыва дружеских отношений или драки в баре, поэтому разработчикам этих игр не нужно беспокоиться о том, что игроки будут перемещать чужие фишки или фигуры или выбрасывать бильярдные шары в окно. Но этих социальных сдерживающих факторов нет в интернете, где каждый прячется за анонимностью и может уйти в любое время. В таких играх дизайн самой игры должен учитывать возможность вредительства.

Первая линия защиты от всех разных целей такая же, как и при деск-джампинге: мотивируйте игроков иметь осмысленные цели. Игроки не придумывают себе разные цели случайно; они делают это в ответ на те же импульсы, которые в первую очередь заставляют их играть в игры. Они хотят побеждать, исследовать, общаться и влиять на людей. Если лучший способ получить это – сыграть в игру по тем правилам, какие были заложены, то они так и сделают.

К сожалению, добиться идеального совпадения целей сразу для всех игроков практически невозможно. Обычно нам нужны другие меры для поддержания многопользовательских игр.

Большое количество игроков является буфером против разных целей. Если в команде из двух человек один из них отлынивает, выходит из игры или занимается вредительством, это гораздо хуже, чем если то же самое происходит в команде из 12 человек.

Иногда конкретные решения могут прояснить конкретные вопросы. Например, в Left 4 Dead могут играть только четыре игрока, а кампании длятся 45 минут. У четырех незнакомых между собой людей, играющих непрерывно в течение этого времени, не такие большие шансы на победу; существуют разные цели, когда один игрок хочет выйти, а другие хотят продолжить играть. Но игра не прерывается, потому что как только игрок уходит, его персонаж управляется ИИ, который управляет им, пока не присоединится другой игрок. ИИ не в состоянии полноценно заменить реального человека, но это вполне действенная стратегия.

Проблемы вредительства нуждаются в более радикальных решениях, чем другие отличные цели, потому что если они возникают, то наносят гораздо больший ущерб.

Один из очевидных вариантов – сделать вредительство невозможным. Если в шутере игрок блокирует двери, разрешите игрокам проходить сквозь друг друга. Если в игре MMO игроки заманивают монстров, чтобы атаковать других игроков в городе, обеспечьте безопасные зоны, куда монстры не пойдут.

Эти строгие ограничения необходимы, чтобы избежать худших случаев, но, к сожалению, мы не можем запретить все возможные стратегии вредительства. Всегда остается некоторая лазейка, даже если это предполагает намеренное поражение или отказ от игры. В стратегиях можно просто спрятать свои боевые единицы по углам и даже не пытаться выиграть. Игрок командного шутера может произвольно стрелять из своего оружия, чтобы указать местоположение своей команды. Возможности безграничны.

Но мы не должны учитывать каждый отдельный случай. Стратегии вредительства можно распределить по шкале степени серьезности в соответствии с их развлекательной ценностью для вредителей и их разрушительным воздействием на других игроков. Самые серьезные стратегии очень интересны для вредителей и разрушают игру для игроков. Стратегии, в которых проблемы отсутствуют, – это стратегии, которые либо не приносят удовольствия вредителю, либо не причиняют вреда другим игрокам. Чтобы игра нормально работала через интернет, разработчики должны выявить наиболее серьезную стратегию вредительства и решить проблему. Если степень серьезности ниже определенного уровня шкалы, бессмысленно перекручивать всю игру, чтобы не допустить вредительства. Например, стратегии остаются интересными для игроков, потому что просто не сражаться вредителю не весело и это не вредит другому игроку, который получает легкую победу (если было скучно). И игроки в шутер могут навредить своей команде, совершив самоубийство, но они этого не делают, потому что смерть – не весело. Эти стратегии вредительства ниже того уровня, когда следует начать беспокоиться. Пока мы запрещаем самые жесткие стратегии вредительства, игра работает.

К сожалению, не все игры можно защитить от вредителей изнутри. Этим играм нужны последние линии защиты в виде механики обеспечения порядка, например системы голосования или модераторы игр. Такие системы неаккуратны и неэлегантны: для голосования необходимо прервать процесс игры, чтобы игроки могли подвести итог собственному опыту, а оплата модераторам стоит разработчикам денег. Но при использовании в качестве последней линии защиты эти системы могут сохранить игру, которая в противном случае превратилась бы в болото заблокированных дверных проемов, игнорируемых целей и непристойного контента.

Разные навыки

Один особый вид разных навыков – тот, который появляется из-за значительной разницы в навыках игроков. Когда один игрок является экспертом, а другой – новичком, могут происходить не самые приятные вещи.

Цель неопытного игрока – изучить игру и не находиться под слишком сильным давлением. Цель опытного игрока – сыграть и выиграть глубокую игру, повышающую уровень мастерства. Различие между этими целями может приводить к конфликтам, которые неприятны для обеих сторон. Неопытный игрок находится под давлением, его оскорбляют. Опытному игроку либо скучно играть против ужасного (по его мнению) противника, либо его раздражает бесполезный член команды.

Это весьма распространенная проблема, потому что она возникает везде, где игроки взаимозависимы, а успех зависит от мастерства. Командные сражения Left 4 Dead, StarCraft II и версия зомби-нацистов в Call of Duty: Black Ops – все это отличные дизайны, и все они страдают от проблемы разных навыков.

Существует несколько способов уменьшить влияние разных навыков. Прежде всего, сократить непосредственно саму разницу в навыках.

Очевидно, что простой элегантный дизайн – лучший способ сокращения разных навыков. Игра, которую легко понять, поможет игрокам быстрее преодолеть границу мастерства, поэтому игроки меньше раздражают экспертов и наслаждаются игрой.

Еще один способ уменьшить различия в навыках – создать алгоритм поиска, который собирает игроков с похожими уровнями мастерства. Система отслеживает уровень опыта каждого игрока и коэффициент выигрыша. Когда игрок ищет игру, алгоритм отправляет его к другим игрокам с похожими показателями. Это концептуально простое решение, но на практике разработка и проектирование этих систем может стать серьезной проблемой.

Бывают и структурные решения. Массовые многопользовательские игры, такие как World of Warcraft, настроены так, что игроки могут играть в одиночку первые несколько часов, не испытывая давления со стороны других игроков, а после того, как они изучат основы, влиться в группу. Иначе говоря, предполагается, что начинающие игроки никогда не должны играть какую-либо роль в командной игре, откуда следует, что они не смогут навредить команде. Аналогичным образом во многих играх как одиночный, так и многопользовательский режим. Прежде чем погрузиться в многопользовательскую игру, игроки сначала учатся в однопользовательском режиме, где их неудачи ни на что не влияют. Это означает, что большинство пользователей, играющих по сети, не будут абсолютными новичками, даже если они не эксперты.

Наконец, игры могут уменьшить разные навыки благодаря хорошему адаптивному обучению. Например, в Left 4 Dead используется адаптивная система обучения, которая сообщает начинающим игрокам алгоритм действий в каждой критической ситуации. Когда зомби-охотник запрыгивает и отключает союзника, на экране мигает сообщение с указанием спасти своего друга. Это происходит при каждом важном действии в игре – выполнение задач, помощь союзникам и получение ресурсов. Таким образом, хотя у новичка может быть плохая цель или сырая стратегия, его, по крайней мере, не оставляют в полной неопределенности.

Если мы не можем уменьшить разницу в навыках, мы можем сделать ее менее важной, а игроков – более независимыми друг от друга. Многие считают взаимозависимость между игроками исключительным благом, но это не так. Поскольку взаимозависимость может создавать чувство общей победы, она также требует, чтобы мы страдали из-за ошибок других людей.

Наилучшим решением является система, которая устраняет общий проигрыш, оставляя при этом общую победу. Например, в таких шутерах, как Halo: Reach, существуют режимы командного боя, в которых игроки сражаются в командах, в основном игнорируя членов своей команды. Но иногда два или три игрока формируют спонтанный альянс, побеждают врага и разбегаются. Так создается командная работа, но только на необязательной, краткосрочной основе, что обеспечивает общую победу, не усиливая общее поражение.

Многие наивные проекты основаны на предположении о том, что игроки будут работать сообща.

И если это предположить, то чудеса кажутся возможными. Но по-настоящему сплоченные игроки с хорошими навыками редко встречаются. Игра, которая на это рассчитывает, долго не протянет. Многопользовательский дизайн должен быть достаточно устойчивым, чтобы справляться с постоянным хаосом, причиной которого являются уход игроков, вредительство, отсутствие ключевых навыков или решение играть не по правилам.